废弃PVC塑料热解过程多尺度反应动力学特性研究

汤元君，李 璇，董 隽，李国能*，罗冠群，王卫民，许友生

（1.浙江科技学院能源与环境系统工程系，杭州 310023；2.浙江浙能技术研究院有限公司，杭州 311121；3.浙江大学能源清洁利用国家重点实验室，杭州 310027）

0 前言

塑料制品由于其优越的性能与低的廉价格广泛应用于日常生活及工农业生产中[1]，但同时也带来了日益严峻的废弃塑料垃圾污染问题。废弃塑料的处理处置问题成为当前面临的巨大的挑战之一。废弃塑料热解技术作为一种新兴的高效塑料处理回收技术，在惰性气氛下可以将塑料加热裂解产生固相、液相及气相高附加值产物，将长链聚合物分子分解成小分子化合物，从而实现废弃塑料向能源燃料或有价值的化学品的高效转化[2]。PVC塑料在塑料制品中占据重要地位[3]。废弃的PVC塑料中含有大量的氯，在热解过程中PVC中的氯在较低温度条件下（＞200℃）即可挥发出来，形成HCl气体，造成设备腐蚀、环境污染等一系列问题。同时，当烟气处于200～400℃范围内时，由于含氯化合物（如HCl、CuCl2等）的存在，会加速二恶英污染物的生成[4]。因此，有必要全面了解和预测废弃PVC塑料的热解反应动力学特性及反应过程机理，以便更好地实现废弃PVC塑料回收利用与控制有害物质的生成。然而，由于PVC组分与结构的复杂性，其热解过程由多步重叠复杂反应组成，这给其反应动力学分析带来了难度，需要将其中的重叠复杂反应进行解卷积分离。Perejon等[5]分析了不同的统计函数应用于重叠反应过程的适用性，结果表明Fraser-Suzuki函数适合于拟合复杂的动力学曲线结构，特别是允许拟合曲线的不对称性，其可以将复杂热解体系中的重叠反应有效分离。Manic等[6，7]分别利用 Fraser-Suzuki函数，在不同升温速率下成功从复杂生物质的多步热解过程中解卷积了3个拟组分，研究了重叠复杂反应过程的动力学特性参数。因此，Fraser-Suzuki函数能够有效实现复杂重叠反应的反卷积，将重叠反应区分以助于实现化学反应动力学特性的预测与表征。

为系统全面地对PVC整个热解过程特性进行研究，本文从整体尺度、失重阶段尺度和复杂重叠反应解卷积尺度3种不同尺度开展PVC热解反应动力学特性与反应机理分析，使用Fraser-Suzuki函数将DTG曲线中的重叠复杂反应进行解卷积并将各拟反应视作一步反应分别求解；在此基础上，采用3种等转化率无模型方法[Friedman法（微分法）[8]、KAS法（积分法）[9，10]及OFW 法（积分法）[11，12]]求解热解过程Eα；同时采用Master plots理论获得不同阶段化学反应的机理函数。从而全面系统地获得PVC塑料热失重过程中的反应动力学特性及反应机理，为新型废塑料高效清洁热解利用技术的开发和应用提供理论基础。

1 实验部分

1.1 主要原料

废弃PVC塑料粉末，粒径低于106 μm，广州市中新塑料有限公司。

1.2 实验设备及条件

塑料粉末使用前在95oC下真空干燥3 h；热解实验在瑞士梅特勒托利多公司Mettler Toledo TGA/DSC3型热重分析仪（TG）上进行，将样品在40 mL/min氮气气氛下分别以5、10、15、20oC/min的升温速率自室温升温至800oC，记录样品在线性升温条件下的热失重特性。

1.3 动力学模型

1.3.1 热解动力学

1.3.2 Fraser-Suzuki反卷积

为了评估每个单步过程的热解动力学，有必要对重叠复杂反应进行反卷积分离。利用Fraser-Suzuki（FS）函数对DTG曲线进行反卷积是实现这一目标的有效方法之一[13]，FS函数可以表示为：

1.3.3 Eα求解

1.3.4 反应机理函数及lnA确定

采用Master plots理论确定各反应阶段反应机理函数 ƒ（α）及对应的A，方程如式（13）和式（14）所示[16，17]。通过对比实验结果求得的 Master plots（dα/dθ）与常见一次反应机理函数（见表1[14]）进行对比（θ为计算过程中的中间变量），为从而得到最合适的反应机理函数ƒ（α）；

表1 常用一次反应机理函数ƒ（α）Tab.1 Commonly used reaction mechanism functionƒ(α)

1.4 多尺度反应动力学特性

从3种不同尺度开展PVC热解反应动力学特性与反应机理分析：（1）整体尺度，将PVC整个热解反应过程视作一步反应，通过KAS法、FWO法及Friedman法与Master plots理论求解其Eα、lnA和反应机理模型；（2）失重阶段尺度，将PVC热解过程的第一失重阶段（243.75～386.50℃）和第二失重阶段（383.00～592.00℃）2个明显独立的失重阶段分别视作一步反应，求解其反应动力学参数；（3）复杂重叠反应解卷积尺度，使用Fraser-Suzuki函数将PVC整个热解过程中的重叠复杂反应进行解卷积，分离为3个独立的拟反应，每个拟反应分别视作一步反应，求解其反应动力学参数。

2 结果与讨论

2.1 PVC热解特性

图1给出了不同升温速率下PVC的TG和DTG曲线。可以看出，在不同升温速率条件下，PVC质量损失从较低温度范围开始（243.70～253.00℃），到中高温范围结束（528.70～592.00℃），在整个温度范围内的质量损失率约为91.16%～91.85%。说明PVC塑料的热解反应在较温和的条件下即可以完全发生，因此适宜采用热解技术对其进行能量、资源回收利用。

图1 不同升温速率下PVC的TG与DTG曲线Fig.1 TG and DTG curves of PVC at different heating rates

PVC在热解过程中存在2个明显的失重阶段，其在不同升温速率下对应的热解特征参数如表2所示，其中Dpk1、Dpk2、Tpk1、Tpk2代表热解第一和第二阶段的最大质量损失速率及其对应的温度；W1、W2代表热解第一和第二阶段的质量损失率。第一失重阶段为243.70～386.50℃，质量损失率为69.82%～70.27%；第二失重阶段为383.00～592.00℃，质量损失率为29.92%～30.12%。需要指出的是，PVC热解虽然存在2个明显的失重阶段，但是其在第一个失重阶段对应的DTG曲线中存在2个明显的峰（图1），说明其在第一阶段失重过程中发生了明显的重叠反应。以往研究表明，PVC热解的2个阶段中，第一阶段主反应为HCl生成反应及少量苯、环烷烃等芳香族化合物生成反应[18]；第二阶段主反应为共轭多烯的重构环化等反应[19]。因此，在进行PVC热解反应动力学特性研究的过程中需要考虑重叠复杂反应的交互影响。

表2 PVC的热解过程Tab.2 Pyrolysis of PVC

升温速率对PVC热解的影响如图1所示。随着升温速率的增加，TG和DTG曲线向高温方向偏移。这是由于样品和熔炉间的温差造成的传热限制导致的[14]。在这种情况下，加热速率越高，热滞后现象越明显，这一现象也存在于其他有关热解实验的研究中[13，20]。

2.2 整体法求解热解动力学特性

常用的热解反应动力学研究方法是将整个反应过程当成整体去求解其反应动力学参数，如Eα等[21，22]。因此，本文首先求解在整体法尺度下，PVC塑料的热解反应动力学特性，通过KAS法、FWO法及Friedman法分别做出ln（β/T2）-1/T的拟合曲线、lnβ-1/T拟合曲线以及ln[β（dα/dT）]-1/T拟合曲线，并通过拟合曲线的斜率计算求解PVC热解整体反应的Eα，如图2所示。可以看出，在大部分的α条件下，拟合情况都比较好；然而，在部分α条件下也存在拟合较差的曲线，如Friedman法下α=0.45～0.55时，曲线的线性相关系数（R2）仅在0.70～0.94之间，此时得到的Eα结果不可靠；尤其需要特别指出的是，α为0.7时，3种方法得到的拟合曲线与其他α条件下得到的拟合曲线呈现完全相反的规律；在大部分α条件下，拟合曲线的斜率都是负值，而当α为0.7时拟合曲线的斜率为正值，这也意味着此时求得的Eα为负值。分析原因主要是α为0.7时，PVC热解过程恰好处于第一阶段失重和第二阶段失重的交界处（如表2所示，第一阶段质量损失率在69.82%～70.27%之间），此时由于PVC热解过程发生了明显的反应阶段变化，从而导致Eα求解曲线规律与其他α条件下不一致，此时计算求解的Eα参数也是不准确的。

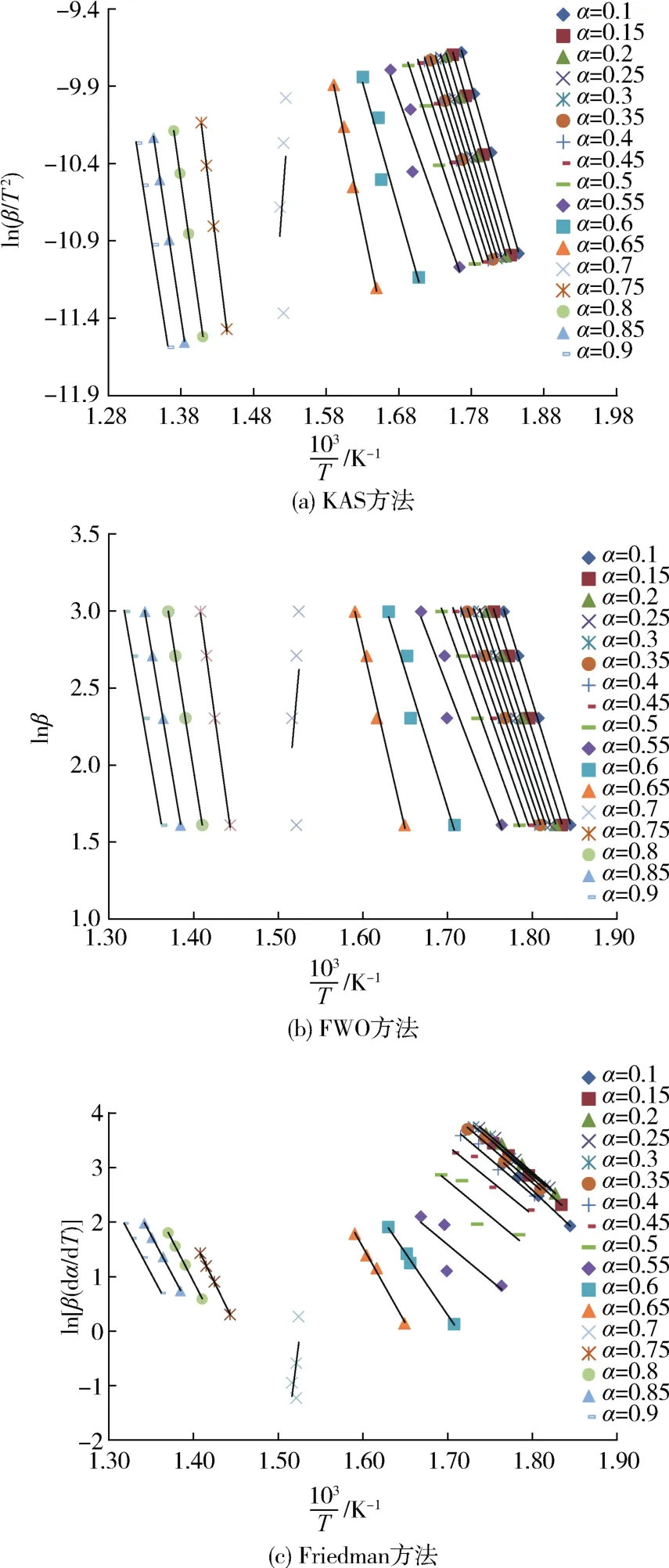
图2 使用不同方法求解PVC的EαFig.2 Determination of Eαvalues of PVC using different methods

基于3种方法求得的Eα随α变化关系如图3所示。可以看出，在不同α范围内，Eα变化幅度较大，偏差率明显大于20%。如前文所述，当Eα的偏差率在20%以上时，说明反应不是由单一反应机制控制，不能采用单步模型充分描述。因此，不能将PVC的整个热解过程当作单一反应机制控制的一步反应，采用整体法求解PVC整个热解过程反应动力学参数不准确。

图3 Eα与α的关系（整体法）Fig.3 Relationship between Eαand α（integrated method）

通过式（13）建立的实验dα/dθ-α曲线与反应机理函数ƒ（α）曲线的对比结果如图4所示。从图中可以看出基于3种方法建立的dα/dθ-α曲线形状与常见的一次反应的机理函数ƒ（α）曲线的形状均不一致，进一步说明PVC塑料的整个热解过程存在多步骤反应，不能用单步反应模型充分描述。

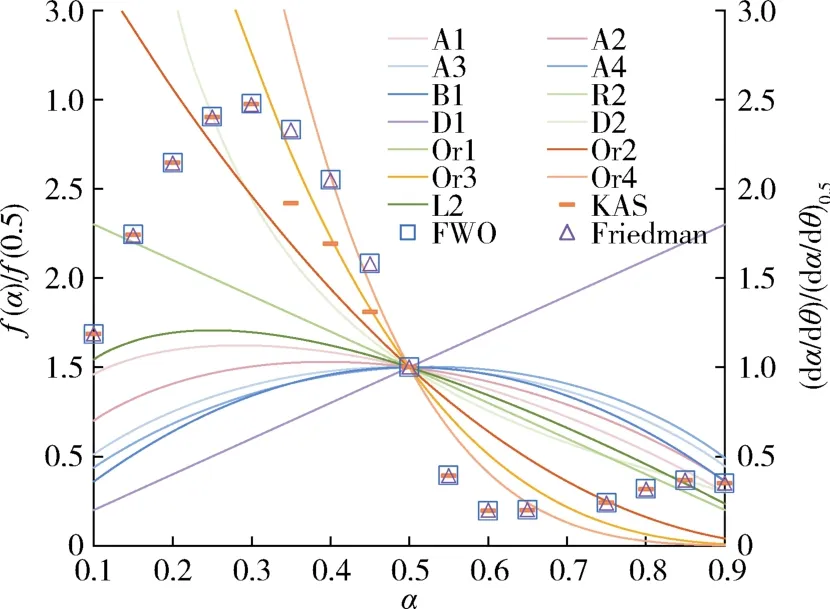
图4 实验主图与机理函数曲线（整体法）Fig.4 Experimental master-plots and mechanism function curves（integrated method）

2.3 失重阶段法求解热解动力学特性

图5为2个失重阶段对应的一次反应求解的Eα-α曲线。可以看出，PVC热解过程第一失重阶段的平均Eα在121.04～132.82 kJ/mol之间，第二失重阶段平均Eα在242.68～266.71 kJ/mol之间。时新刚等[23]计算的PVC热解第一失重阶段的Eα为50 kJ/mol左右，第二阶段的Eα为245 kJ/mol左右；师奇松等[24]计算的该值为40～70 kJ/mol和5 kJ/mol左右。可见，已有的文献数据存在不一致之处，这可能是由于使用的热重温度程序、设备及选用的PVC塑料样品差异导致。

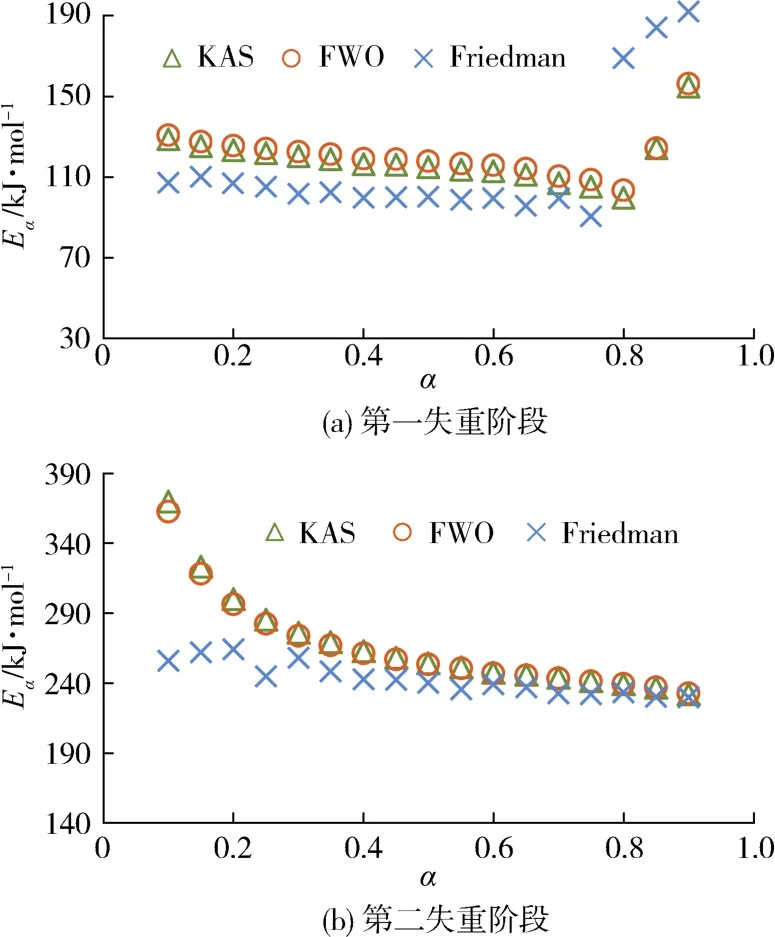
图5 Eα与α的关系（失重阶段法）Fig.5 Relationship between Eα and α（weight loss stage method）

需要进一步指出的是，对于PVC热解过程中第二失重阶段，其Eα随α基本保持不变，偏差率在20%范围以内，表明此阶段遵循单级反应过程，可以使用单步反应模型充分描述[25]。而反观PVC热解过程的第一失重阶段，当α在0.1～0.7之间时，其Eα的偏差率在0.27%～9.74%之间，表明该阶段发生的失重反应可能遵循单一反应机制控制；然而，当α在0.7～0.9之间时，Eα明显增大，偏差率大于20%，说明在该阶段内可能发生了其他的化学反应。这也印证了前文所述PVC热解第一失重阶段不是由单一化学反应组成的，而是存在多步骤的复杂重叠反应。

实验主图与常见一步反应机理函数曲线对比如图6所示。从图中可以看出第一失重阶段的实验主图曲线（dαdθ-α曲线）形状与选用的常见一次反应机理函数曲线的形状均不一致，说明该阶段反应不是由常见单一反应机制控制的化学反应；而第二失重阶段建立的dα/dθ-α曲线形状与反应机理函数（A4 Avrami-Erofeev）ƒ（α）=4（1-α）[-ln（1-α）]3/4曲线的形状基本一致，说明PVC热解过程的第二失重阶段发生的化学反应是由（A4 Avrami-Erofeev）ƒ（α）=4（1-α）[-ln（1-α）]3/4反应机理控制的一步式的化学反应组成。

2.4 Fraser-Suzuki反卷积法求解热解动力学特性

如前文所述，PVC的热解主要由3个主反应构成，其中热重曲线第一失重阶段包含了2个主反应，首先发生脱氢氯化形成HCl和多烯，随后产生的多烯分子经过缩合和脱烷基反应形成苯和芳香族化合物；第二失重阶段为多烯分子发生环化和交联，形成多环芳香烃[26，27]。但是按PVC热解过程不同失重阶段求解反应过程动力学特性无法分离第一失重阶段发生的重叠复杂反应。因此，还需要将第一失重阶段的重叠复杂反应分离出来。对于这类重叠复杂反应的动力学分析，通常会使用Lorentzian函数、Gaussian函数、Weibull函数和Fraser-Suzuki函数等统计函数[28]。其中，Fraser-Suzuki函数由于其允许拟合曲线的不对称性，更适用于拟合复杂重叠化学反应的曲线结构，其可以将复杂热解体系中的重叠复杂化学反应有效分离开，其求解过程如式（7）所示。

在不同升温速率条件下，PVC塑料热解过程Fraser-Suzuki复杂重叠反应反卷积曲线如图7所示。按照上述结论将整个DTG曲线分离为3个单独的拟反应，分别记做拟反应FS1（脱氢氯化形成HCl反应）、拟反应FS2（多烯分子缩合脱烷基形成芳香化合物反应）、和拟反应FS3（多烯分子环化交联生成多环芳烃反应）。分峰后各拟反应dα/dt之值总和与实际实验结果之间的偏差在1.40%～1.82%范围之内，分峰拟合结果能够较好地反映热解过程的实际转化过程。具体到分离后的3个拟反应，以15℃/min升温速率条件下的拟合结果为例，3个单独的拟反应FS1、FS2与FS3发生的温度范围分别在267.75～333.73℃、286.00～398.00℃与386.75～581.00℃。从分峰拟合的结果中可以发现拟反应FS1与FS2在286.00～333.73℃温度范围内有明显重叠，这也与前文采用失重阶段法分析过程中第一失重阶段a在0.7到0.9时的温度区间278.38～312.96℃相对应，进一步说明在此温度范围内，PVC热解发生了复杂的重叠反应。

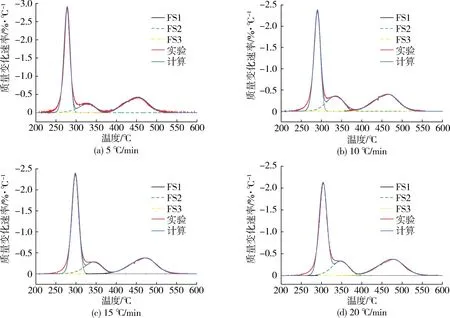
图7 不同升温速率下PVC DTG曲线反卷积结果Fig.7 Deconvoluted DTG curves of PVC at heating rate of 5，10，15 and 20 ℃/min

针对Fraser-Suzuki分峰后获得的3个拟反应，分别做出求解Eα线图并进行拟合，结果如图8所示。从图中可以看出3种方法计算得到的每个拟反应的Eα分布具有相似的趋势，在α较小或较大位置时，Eα值有一定的偏差，这可能主要是由于温度积分近似或峰值尾部基线插值产生的误差所导致[29]。Friedman法与KAS法、FWO法得到的Eα值相比存在一定的偏差，这主要是由于微分法与积分法在数据收集时产生的截断误差以及数值微分计算时的不稳定造成的[30]。在整个α范围内，各拟反应Eα的偏差率都在20%之内，可以说明PVC各拟反应可能由单一反应机制控制，可以分别用单步模型充分描述。各拟反应的Eα平均值如表4所示。可以看出，FS1、FS2和 FS3的Eα平均值分别在108.50～128.01、182.34～222.22 kJ/mol、233.06～246.49 kJ/mol范围内，这与Ephraim等[14]采用KAS法获得的结果相似，其计算得到的3个阶段的Eα分别为120.00、112.00、226.00 kJ/mol。

图8 Eα与α的关系（按FS解卷积法）Fig.8 Relationship between Eα and α（Fraser-Suzuki deconvolution method）

实验主图与机理函数曲线的对比如图9所示。从图中可以看出PVC塑料热解的拟反应FS1和FS3建立的dα/dθ-α曲线形状与常见一次反应机理函数A4 Avrami-Erofeev：ƒ（α）=4（1-α）[-ln（1-α）]3/4曲线的形状基本一致；而FS2与选用的常见一次反应机理函数B1 Prout-Trompkins：ƒ（α）=α（1-α）曲线的形状基本一致。说明PVC塑料热解的各拟反应FS1、FS2及FS3都可以被认为是由确定单一反应机制控制的单步主化学反应。

图9 实验主图与机理函数曲线（按FS解卷积法）Fig.9 Experimental master-plots and mechanism function curves（Fraser-Suzuki deconvolution method）

在获得PVC塑料热解各拟反应最适合反应机理模型函数基础上，求解各拟反应动力学方程的lnA，如式（9）～（11）所示，各拟反应 FS1、FS2、FS3的lnA值如表3所示。因此，根据求得的反应动力学三要素即Eα、lnA、f（α），可以得到PVC热解反应的动力学方程，如式（15）～（17）所示（以KAS法结果为例）。在此基础上，对式（15）～（17）进行整理并两边积分，等式左侧为关于α的积分，右侧为仅与温度T有关的积分，这样可以得到α与T之间的关系。同时，由于α仅与PVC失重质量（m）有关，因此可以通过α与T之间的关系导出m与T之间的数学关系模型，从而实现PVC热解反应过程的重建与预测。

表3 Fraser-Suzuki函数解卷积下各拟反应动力学参数Tab.3 Kinetic parameters of proposed reactions under Fraser-Suzuki function deconvolution

3 结论

（1）通过整体尺度法和失重阶段尺度法均无法准确求解反应动力学参数；

（2）采用复杂重叠反应Fraser-Suzuki反卷积尺度法能够较为准确地求解PVC热解过程的反应动力学参数；整个热解过程可分离为3个独立的主反应，各反应占比分别为47.37%～55.38%、12.70%～19.24%和29.97%～31.28%；其Eα分别为108.50～130.57、182.34～222.22、233.06～246.49 kJ/mol；lnA值 分 别 为 19.85～39.94、26.99～47.16、33.27～50.93 s-1；拟反应FS1和FS3符合反应机理函数A4 Avrami-Erofeev：ƒ（α）=4（1-α）[-ln（1-α）]3/4，拟反应FS2符合反应机理函数B1 Prout-Trompkins：ƒ（α）=α（1-α）；

（3）获得的PVC热解反应动力学方程可便于分析预测废弃PVC塑料热解利用过程中的热解反应特性，为实现塑料废弃物清洁高效能源化与资源化利用奠定理论基础。