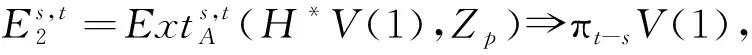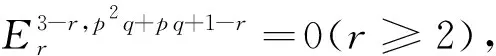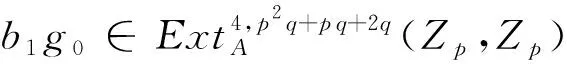谱V(1)同伦群中一些元素的存在性
2022-06-09蔡玉梅李园园王玉玉
蔡玉梅, 李园园, 王玉玉
(天津师范大学数学科学学院, 天津 300387)
全文中A为模p的Steenrod代数,P为由所有A的循环缩减幂pi(i≥0)生成的子代数.同伦群是拓扑空间的几个基本的代数不变量之一.相较于同调群,同伦群的计算十分困难,亦成为代数拓扑的重要问题之一.对于简单的不可缩空间球面,它的同伦群,特别是稳定同伦群就更是有重要意义,近几年的相关成果参见文献[1-4].


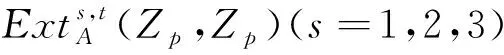
和
由文献[8],Toda-Smith谱与球谱S通过一些上纤维化存在密切联系.因此,它们的同伦群中元素的存在性亦相互影响关联.本文即是发掘了谱V(1)同伦群中的一些非平凡元素,其在Adams谱序列中分别由b1h1,b1g0表示.
本文的主要结果如下.
定理令p≥7,q=2(p-1),


均在Adams谱序列中是永久循环,且收敛到π*V(1)中的非零元,其中映射i0、i1具体形式见第一节所述上纤维序列内容.
全文中|·|为元素的全次数,Fdim为元素的第一次数,Sdim为元素的第二次数.
1May谱序列和Ext群的相关结论
Toda-Smith谱V(n)的Zp上同调群为H*V(n)≅E[Q0,Q1,…,Qn]≅Q(2n+1),其中Qi(i=0,1,…,n)是模pSteenrod代数A的Milnor基元,E[]是外代数.由文献[8],V(n)是可实现的,当n=0,1,2,3且p>2n时,存在上纤维序列:
其中,V(-1)=S,αn分别为p,α,β,γ(当n=0,1,2,3时),并且由此上纤维序列可以导出Ext群的长正合序列.



以下命题3~6均是在p≥7,r≥2的情况下.



表1 生成元λ及其全次数|λ| (mod p q-2)之余数Tab.1 Generator λ and the remainder of total degree |λ| (mod p q-2)
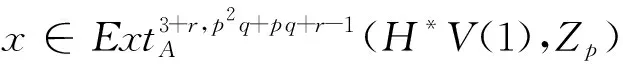

知(i2)*(x)=(α3)*(x1),其中,
所以,
(i2)*(x)=(α3)*(x1)=0.
因此由正合性,存在
满足(α2)*(z1)=x.
归纳假设,存在
满足

Q=|(i3)*(i2)*(zk)|=
p2q+pq+r-1-k(2p2-1)-(3+r-k)=
(1-k)q-2k(modpq-2).
A1当k=1时,Q=-2(modpq-2),知没有满足条件的对应元,故(i3)*(i2)*(zk)=0.
A2当1 或者 A3当k=p-2+r时,其中r=0,1,Q=(2-r)q-2r(modpq-2). A3.1r=0,Q=2q(modpq-2),由表1知存在满足条件的元λ可能为g0,h2h0,其全次数分别为pq+2q-2,p2q+q-2,与(i3)*(i2)*(zk)的全次数不相等,所以(i3)*(i2)*(zk)=0. A3.2r=1,Q=q-2(modpq-2),此种情形也没有对应元,故(i3)*(i2)*(zk)=0. A4当k>p-1时,|(i3)*(i2)*(zk)|<0.因此(i3)*(i2)*(zk)=0. 完成了归纳. 证明当r>3时,命题显然成立.下面考虑2≤r≤3的情形. 0=(i3)*(i2)*(x′)∈ 由序列正合性,存在 满足x′=(α2)*(z1′). 归纳假设,存在 满足 由于Fdim=3-r-k≥0且2≤r≤3,k≥1,则k只能取1,此时|(i3)*(i2)*(z1′)|=p2q-q-2=0(modpq-2),由表1易知无对应元,因此(i3)*(i2)*(zk′)=0.由正合性存在 x2′∈ 满足(i2)*(zk′)=(α3)*(x2′)=0.因此存在 zk+1′∈ 满足 完成了归纳. 表2 生成元 λ 及其全次数 |λ| (mod p q-2) 之余数Tab.2 Generator λ and the remainder of total degree |λ| (mod p q-2) (i3)*(i2)*(y)∈ (i3)*(y1)∈ 归纳假设,存在 满足 N=|(i3)*(i2)*(wk)|= p2q+pq+2q+r-1-k(2p2-1)-4-r+k= (3-k)q-(2k+1)(modpq-2). B1当k=1时,N=2q-3(modpq-2);k=2时,N=q-5(modpq-2);k=3时,N=-7(modpq-2).由May谱序列的各个生成元及表2知,这几种情形均无对应元,故(i3)*(i2)*(wk)=0. B2当3 或者 设|λ|=aq+b(modpq-2),从表2中可知0≤a≤3,显然与q的系数3+p-k>6和2+p-k>5矛盾,所以前者和后者的情形均没有满足与其次数对应的元,即(i3)*(i2)*(wk)=0. B3当k=p-3+r时,N=(5-r)q+1-2r(modpq-2),其中r=0,1,2,3.类似上述讨论知,在表2中没有元λ满足|λ|=(5-r)q+1-2r(modpq-2),故(i3)*(i2)*(wk)=0. B4当k>p时,|(i3)*(i2)*(wk)|<0.因此(i3)*(i2)*(wk)=0. 满足(α2)*(wk+1)=wk,即 完成了归纳. 证明当r>4时,命题显然成立.下面考虑2≤r≤4的情形. 所以(i2)*(y′)=(α3)*(α3)*(y2′)=0.由序列正合性,存在 满足(α2)*(w1′)=y′. 归纳假设,存在 满足 由于Fdim=4-r-k≥0且2≤r≤4,k≥1,则k只能取1,2.对于wk′,其全次数 M=p2q+pq+2q+1-r- k(2p2-1)-(4-r-k)= (3-k)q+1-2k(modpq-2). C2当k=2时,M=q-3(modpq-2),显然在表2中没有元u满足|u|=q-3(modpq-2),故(i3)*(i2)*(wk′)=0.所以存在 (H*V(2),Zp)=0, 满足(i2)*(wk′)=(α3)*(y3′)=0.因此存在 (H*V(1),Zp), 满足(α2)*(wk+1′)=wk′,即 完成了归纳. 0(r≥2), 在Adams谱序列里是永久循环.由命题4, 0(r≥2), 下的像,则 所以 在Adams谱序列里是永久循环.由命题6,

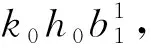
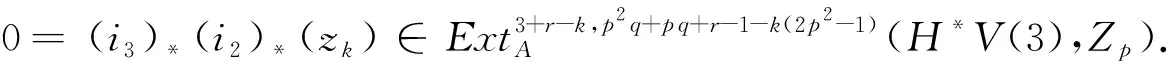


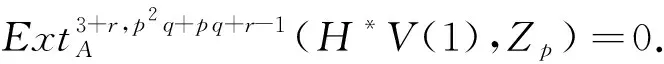














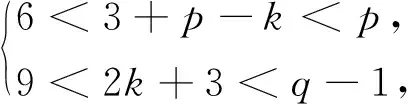


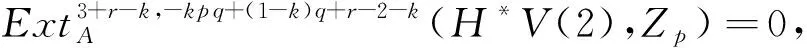
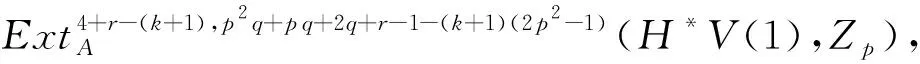

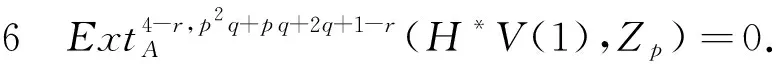






2定理的证明