基于磁流变原理的复合天棚控制算法的改进与优化
2022-06-09祝世兴赵玉彬祝恒佳
祝世兴,赵玉彬,魏 戬,祝恒佳
(1.中国民航大学 航空工程学院,天津 300300;2.昆明理工大学 机电工程学院,云南 昆明 650000)
减震器是起落架系统的重要部件,其参数选择极大影响通航飞机滑跑过程的安全性与舒适性。传统飞机起落架属于被动控制,为了适应着陆过程的减震,往往选择较大刚度及阻尼系数。而对于中低速滑跑过程,较大的阻尼系数会影响飞机滑跑过程平顺性。为探究改善通航飞机滑跑过程的平顺性要求,阻尼系数的选择显得尤为关键。依据动力源及调节对象的不同,可控阻尼器分为半主动控制与主动控制[1]。半主动控制兼具主被动控制的优点[2],且可达到媲美主动控制的效果[3]。磁流变液阻尼器可以通过调节电流改变磁场强度,进而改变输出阻尼力[4],且属于响应速度在毫秒级的智能流体减震器[5]。利用磁流变阻尼器对滑跑过程进行减振控制时,高效的控制策略是半主动控制的必备条件。
随着阻尼比控制与半主动控制技术的发展,国内外学者进行了广泛而深入的研究。文献[6]利用Adms对减振过程进行动力学分析,讨论了阻尼系数与减振器刚度对平顺性指标的影响。文献[7]将不同刚度与阻尼匹配,实现对不同路面条件下最优参数的平顺性优化。除了针对阻尼器参数的优化,半主动控制策略的改进也尤为重要。因此,文献[8]采用开关模式整流器(SMR)改进天棚控制策略,相比传统的天棚半主动控制策略,提升了安全性与舒适性。文献[9]选择最小穿越速度作为地棚控制目标函数,相比传统开关型地棚控制,可有效提升综合减振性能。然而,大多数研究仅局限于控制算法本身,缺乏与控制方法的结合。因此,文献[10]采用复合模糊控制进行减振,相比被动控制与传统天棚控制,可以有效降低加速度与轮胎跳动响应值。到目前为止,针对飞机起落架滑跑过程阻尼系数的优化仍然缺少相关的算例与研究。
本文利用Matlab Simulink平台进行建模仿真实验,分析发现阻尼系数过大不利于提升平顺性。基于仿真结果,将压缩与复原行程阻尼约束在限制范围内,再结合天棚控制和地棚控制规律,针对不同的阻尼系数进行迭代仿真实验,寻找最优阻尼参数,进而提出一种改进的复合天棚控制策略。结合飞机滑跑过程运动学模型仿真分析验证该策略的有效性。
1 飞机滑跑过程模型建立
1.1 系统运动微分方程
将机体简化为以下二自由度模型,机体质量可以视为簧载质量,轮胎及阻尼器部分视为非簧载质量;减震器简化为定刚度弹簧与阻尼器的并联;将轮胎视作定刚度簧载系统;路面时域激励信号按照搭建的仿真模块进行输出。飞机滑跑过程运动学二自由度模型如图1所示。

图1 飞机滑跑过程运动学二自由度模型Fig.1 Kinematic model of aircraft taxiing process with two degrees of freedom
依据牛顿定律,可得系统微分方程为
(1)

1.2 路面激励的生成
建立路面时域信号Simulink模型,进而将路面信号输入到仿真系统中。由文献[11]可知,机轮所受路面激励可描述为
(2)
其中:q(t)为路面激励信号;α为路面等级相关参数,可通过相关标准查询;v为机体速度;ω(t)为白噪音信号,其协方差计算公式为
cov[ω(t)]=E[ω(t)ω(t+τ)]=
2ρ2αvδ(t)。
(3)
其中,ρ为路面等级相关参数。 本文选取C级路面, 滑跑速度为30 m/s。 参照文献[12], 可得α=0.11 m-1,ρ2=0.151 m。
将搭建的路面激励生成仿真模型嵌套在Simulink子系统模块中,如图2所示,生成的路面时域随机激励如图3所示。

图2 路面激励生成模块Fig.2 Road excitation generation module

图3 路面激励仿真示意图Fig.3 Schematic diagram of road excitation simulation
1.3 磁流变减震器模型
本文采用中国民航大学自主研发的磁流变阻尼器实现阻尼力输出,利用力学实验台对其进行性能测试,结合仿真结果进行可控阻尼力的输出。
磁流变阻尼器输出阻尼力模型可表示为
(4)
其中:Fb表示磁流变减震器总阻尼力;Fη表示黏滞阻尼力,仅仅与结构尺寸和相对速度有关;Fτ表示库伦阻尼力,与结构尺寸和可控电流有关,是可调可控的阻尼力。相应参数如表1所示。
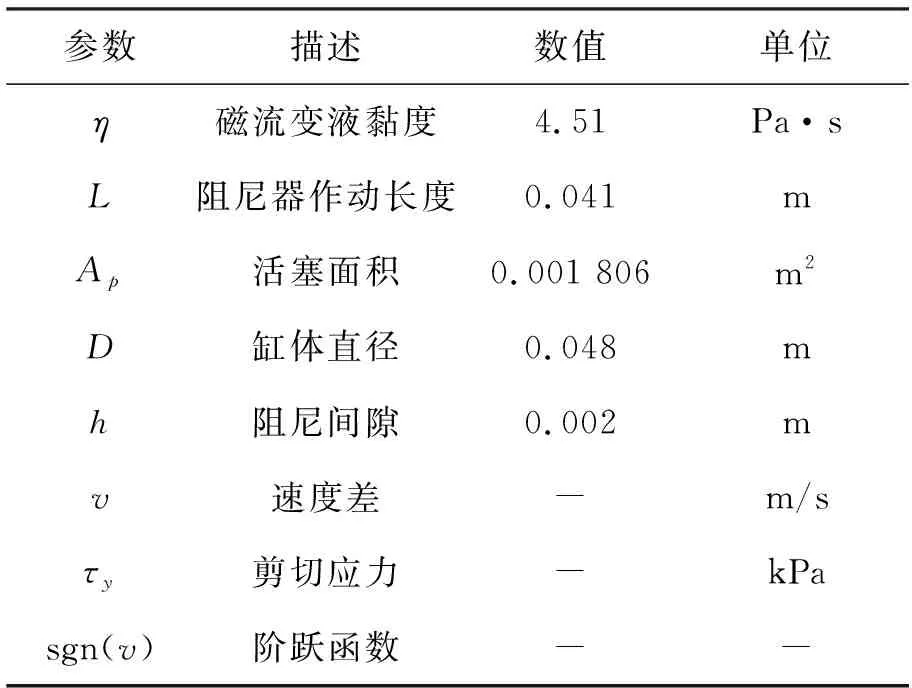
表1 阻尼器模型参数Tab.1 Damper model parameters
Fc=qτy+cvν。
(5)
其中:Fc表示磁流变阻尼器输出阻尼力;q表示库伦阻尼力系数;cv表示黏滞阻尼系数。 将表1的实验参数代入式(5), 结合阻尼器参数计算得cv=5 985.94,q=0.111。
依据磁流变阻尼器力学特性实验数据,将剪切应力与电流强度关系拟合如图4所示。

图4 剪切应力与电流强度关系Fig.4 Relationship between shear stress and current intensity
利用Matlab平台Curve fitting tool工具箱将数据拟合为三次多项式,既保证了数据输出精度,又避免了龙格效应造成数据发散。待拟合的三次特征多项式可表示为
τy=ai3+bi2+ci+d。
(6)
其中, Curve fitting tool工具箱拟合参数a=-2.76,b=14.30,c=4.79,d=-0.51。通过数据拟合过程实现可控阻尼力的可控输出。
由于采用Simulink平台Saturation环节进行阻尼力限制,需要对磁流变阻尼器进行等效力替代,其等效阻尼力公式可表示为
Fd=cdν。
(7)
其中:Fd为等效阻尼力;cd为等效阻尼系数。
将磁流变阻尼器阻尼力Fc等效表示为传统被动式阻尼器阻尼力Fd形式,
Fc=Fd。
(8)
依据磁流变阻尼力相关公式,将式(5)、式(7)代入式(8),则等效阻尼系数可表示为
(9)
将式(6)代入式(9),可得
(10)
将拟合后的数据代入式(10),
4.79i-0.51)+5 985.94。
(11)
本文依靠该磁流变减震器模型作为复合天棚控制策略的阻尼力输出,并将其力学特性嵌入到系统仿真模块中。
1.4 系统仿真模型建立
对于微分方程组(1),基于Simulink平台搭建运动学仿真模块如图5所示。
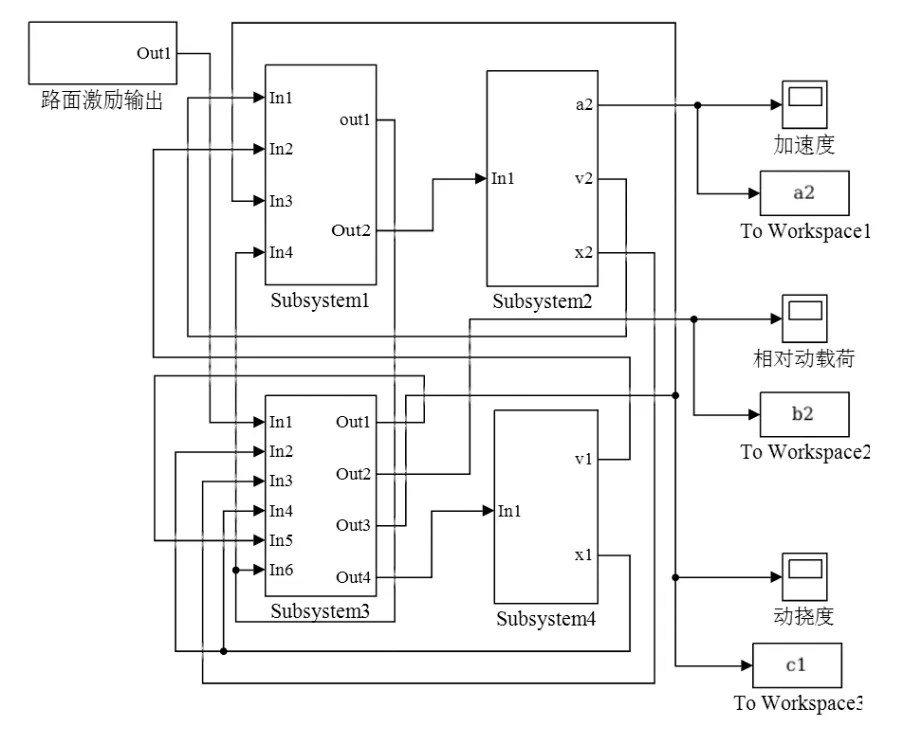
图5 二自由度模型Simulink示意图Fig.5 Schematic diagram of Simulink model with two degrees of freedom
2 限阻尼系数模块的搭建
本节通过引入某型无人机结构参数,将不同的压缩行程阻尼与复原行程阻尼输入到基于Matlab Simulink仿真平台所搭建的二自由度模型中,并进行二维数组仿真,对仿真结果分析,得到最优阻尼系数区间,从而求解出限阻尼系数模块的限制区间。
2.1 算例简介
本文选取某型无人机进行仿真实验。已知阻尼力方程为
(12)

2.2 仿真结果分析
依据图6所示, 随着阻尼系数的增加, 加速度均方根值逐渐减小, 在压缩、 复原阻尼系数为6 000~10 000 N·s/m时,加速度均方根值达到最低;随后,随着压缩及复原行程阻尼系数继续增加,加速度均方根值略有上升;当压缩行程与复原行程阻尼相差过大,加速度均方根值增幅明显。

图6 加速度均方根值等值线图Fig.6 Contour map of RMS value of acceleration
依据图7所示,随着阻尼系数增加,相对动载荷均方根值明显减小;压缩行程阻尼与复原行程阻尼相差较大时,相对动载荷均方根值抑制效果较差;当二者均等比例增大时,相对动载荷均方根值得到明显抑制。

图7 相对动载荷均方根值等值线图Fig.7 Contour map of RMS value of relative dynamic loads
依据图8所示,随着阻尼系数增大,动载荷均方根值会逐渐减小;但当压缩阻尼系数与复原阻尼系数相差过大时,会造成动挠度急剧增加;当复原阻尼系数与压缩阻尼系数等值增大时,动挠度会显著减小。
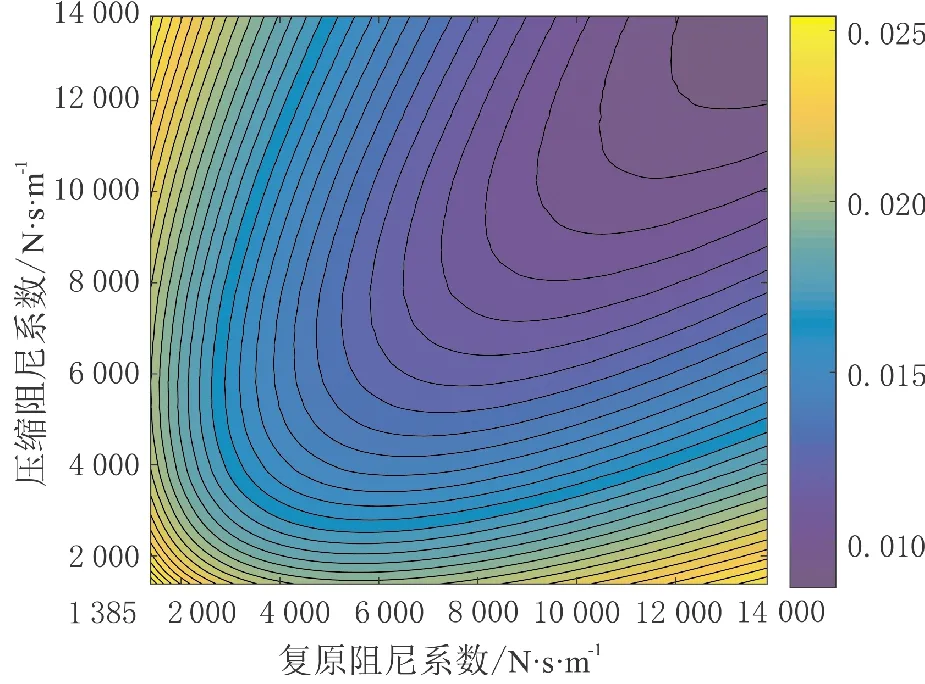
图8 动挠度均方根值等值线图Fig.8 Contour map of RMS value of dynamic deflection
虽然起落架的主要用途是起降,但滑跑过程也是极其重要的一环。为减少起降时冲击载荷,往往会选取较大的阻尼系数进行减震,以便飞机起落架在较短时间内吸收冲击动能。但通过仿真结果分析表明,阻尼系数过大会导致机体加速度增加,进而恶化滑跑过程的平顺性;对于相对动载荷,等值增加阻尼系数有利于减少其均方根值;对于滑跑过程动挠度,压缩行程与复原行程阻尼系数相差较多反而会导致动挠度均方根值增加。为减小滑跑过程加速度均方根值、相对动载荷均方根值及动挠度均方根值,提出一种合理且均衡的控制规律显得尤为关键。经综合分析得出,限阻尼系数区间为6 000~10 000 N·s/m。
3 复合天棚控制算法的模型搭建
基于加速度的特性规律曲线,采用Matlab Simulink平台的Saturation子模块进行阻尼系数限制。通过引入天棚阻尼控制与地棚阻尼控制,构建复合天棚控制算法模型。
3.1 天棚阻尼控制
天棚阻尼控制的思想是在簧载质量与假想的天棚之间安装一个天棚阻尼器[14]。通过分析簧载质量速度方向及簧载质量速度与非簧载质量速度差值速度方向,进而判断天棚阻尼系数的大小。天棚阻尼控制原理如图9所示。

图9 天棚阻尼控制示意图Fig.9 Diagram of sky-hook damping control
传统意义上的天棚阻尼控制规律为
(13)
其中:cs为天棚阻尼系数;cmax和cmin分别表示输出较大和较小的阻尼系数,进而将天棚阻尼力控制规律改进为
(14)
其中,Fs为天棚阻尼力。传统天棚阻尼控制可以有效减少簧载质量加速度均方根值,但难以抑制相对动载荷均方根值的增加,即无法有效提升滑跑过程的操控稳定性。为改善飞机滑跑过程平顺性,采用复合天棚控制策略,并通过Simulink平台进行迭代仿真优化天棚阻尼系数,进而选择最优阻尼系数。
3.2 地棚阻尼控制
地棚阻尼控制的思想是在非簧载质量与假想的地棚之间安装一个地棚阻尼器[15]。地棚阻尼控制将非簧载质量振动速度作为输入量进行控制。地棚阻尼控制原理如图10所示。

图10 地棚阻尼控制示意图Fig.10 Schematic diagram of ground-hook damping control
传统意义上的地棚阻尼控制规律为
(15)
其中,cg为地棚阻尼系数。进而将地棚阻尼力控制规律改进为
(16)
其中,Fg为地棚阻尼力。传统地棚阻尼控制能有效抑制非簧载质量振动,即可以减少相对动载荷均方根值,但对动挠度均方根值的抑制能力较弱,无法有效减少滑跑过程非簧载质量位移。为改善飞机滑跑过程平顺性,采用复合天棚控制算法,并通过Simulink平台进行迭代仿真,优化阻尼系数,进而选择最优地棚阻尼系数。
3.3 阻尼系数限制模块
由于引入复合控制算法会造成相对阻尼系数过大,通过对阻尼系数的限制实现对加速度均方根值的减小。未加限制的阻尼系数如图11所示。利用Saturation仿真控制模块实现对阻尼系数的限制,将阻尼系数限定为[6 000,10 000]之间,其仿真模块如图12所示,输出结果如图13所示。
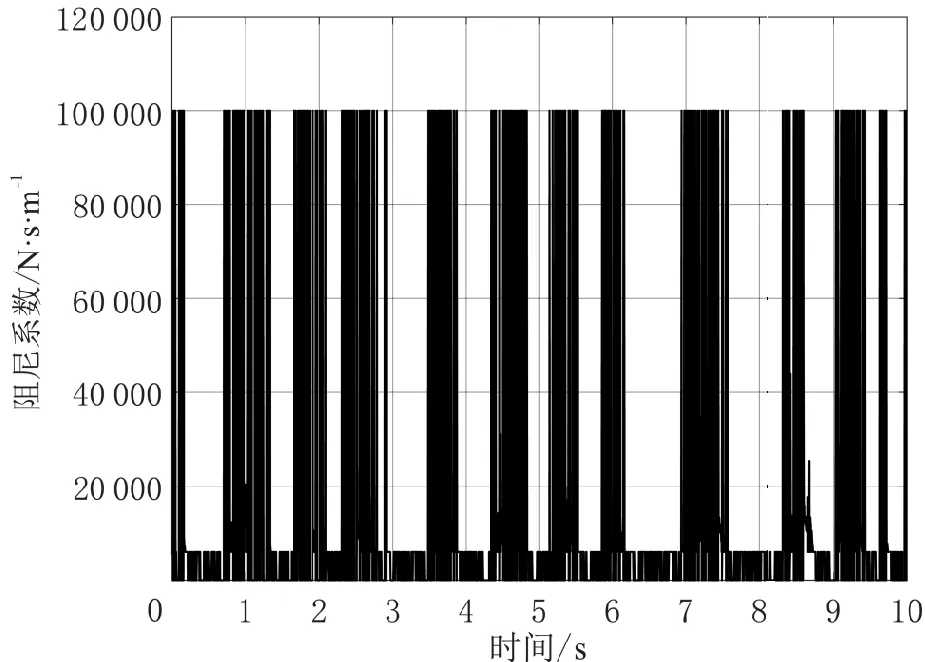
图11 未加限制的阻尼系数Fig.11 Unrestricted damping coefficient
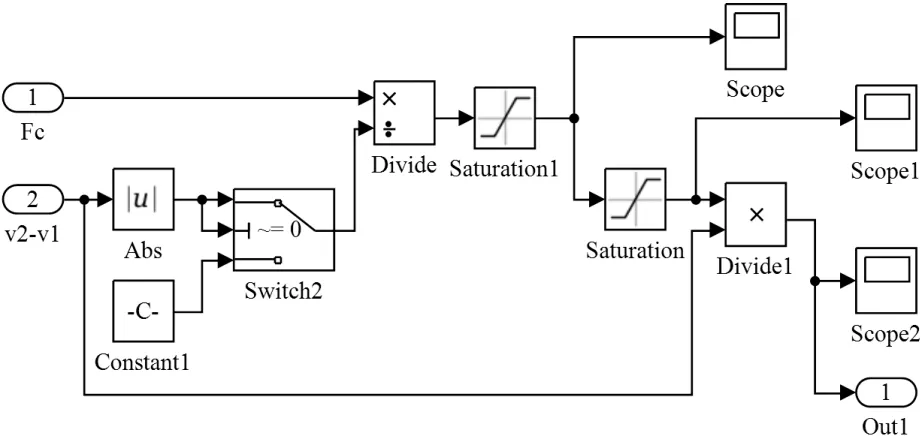
图12 Saturation模块示意图Fig.12 Diagram of Saturation module

图13 增加限制的阻尼系数Fig.13 The damping coefficient of the additional limit
由于初始被动阻尼设定为8 000 N·s/m,因此,未施加限制的阻尼系数会在某些控制情况下过大,会造成加速度激增。施加阻尼系数限制后,阻尼系数将保持在限定范围内,保证加速度处于最优范围内。
3.4 复合天棚控制模型
现将天棚阻尼控制、地棚阻尼控制以及阻尼系数限制控制策略的优点结合,综合改进飞机滑跑过程的平顺性,并优化相应的天棚阻尼系数及地棚阻尼系数,设计出一种能有效改善飞机滑跑过程平顺性的复合天棚控制策略,其二自由度模型如图14所示。
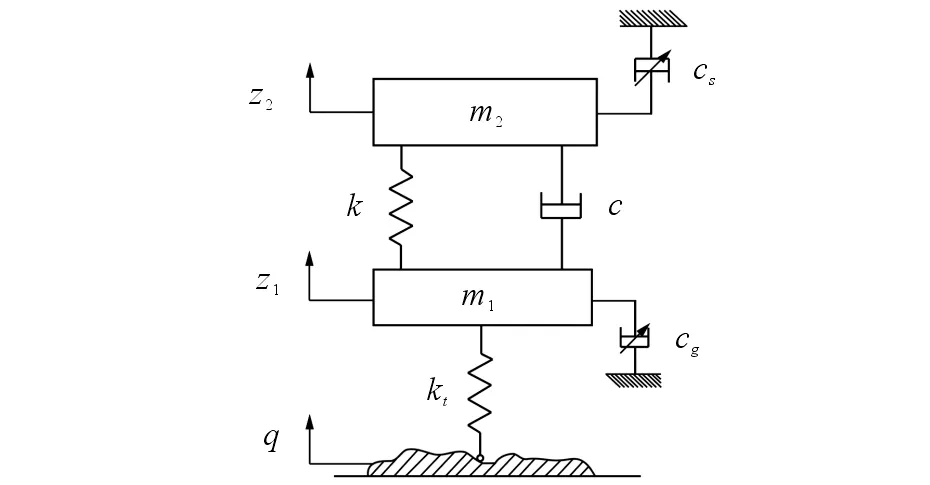
图14 复合天棚控制二自由度模型Fig.14 Compound sky-hook control two degrees of freedom model
复合天棚控制二自由度模型动力学微分方程组为
(17)
4 复合天棚控制算法的仿真优化
将建立的复合天棚控制模块嵌套在机体滑跑过程动力学模型中,选取不同的天棚阻尼值与地棚阻尼值进行迭代仿真,通过仿真结果选择出最优阻尼系数。仿真运行时长1 s,步长选取0.05 s。
4.1 仿真
本例取被动阻尼系数为6 000 N·s/m。天棚阻尼系数取值为[1 000,20 000],等均值分10份,选取天棚阻尼系数共11个数值;地棚阻尼系数取值为[1 000,20 000],等均值分10份,选取地棚阻尼系数共11个数值。共进行11×11次仿真,可得3×121个阻尼匹配序列。通过对仿真模块输入不同的天棚阻尼系数与地棚阻尼系数建立三维坐标系,结果为图15~图17所示。

图15 不同阻尼系数下加速度均方根值等值线图Fig.15 Contour map of RMS values of acceleration under different damping coefficients
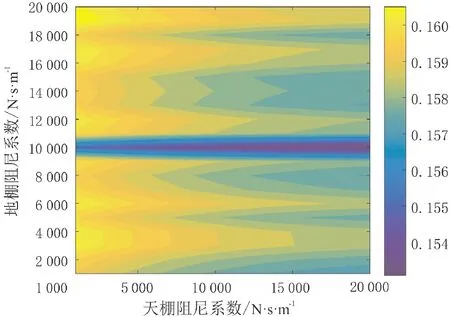
图16 不同阻尼系数下相对动载荷均方根值等值线图Fig.16 Contour map of RMS values of relative dynamic loads under different damping coefficients
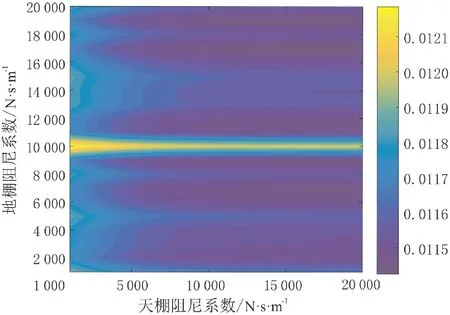
图17 不同阻尼系数下动挠度均方根值等值线图Fig.17 Contour map of RMS values of dynamic deflection under different damping coefficients
4.2 分析
由仿真结果图15~图17可以看出,相比地棚阻尼系数,天棚阻尼系数影响不大。当地棚阻尼系数为10 000 N·s/m时,加速度均方根值与相对动载荷下降明显,但动挠度却上升剧烈。排除仿真实验的局限性以及相应误差,造成动挠度变化异常的原因为Saturation环节对阻尼系数进行数值限定,在确保加速度均方根值最小的前提下,地棚阻尼控制难以完全发挥其半主动控制效果,受限的阻尼系数无法对动挠度提供有效限制。因此,选择地棚阻尼系数为10 000 N·s/m。
对天棚阻尼系数的变化, 滑跑平顺性表现出一定的鲁棒性, 仅在较大天棚阻尼和较小天棚阻尼下表现出小幅差异。 天棚阻尼系数在4 000~8 000 N·s/m之间,加速度均方根值有一定幅度减小,相对动载荷偏大;当天棚阻尼系数在16 000~20 000 N·s/m时,相对动载荷有一定幅度减小,加速度相对偏大。对此可以进行模式选择,当飞机滑跑过程中无需变换前进方向时,可选取较小的天棚阻尼系数;当飞机需要进行改选跑道时,适当增加天棚阻尼系数有利于减少相对动载荷,进而增加可操纵性。选取较小的天棚阻尼系数也更利于磁流变阻尼器温度的耗散,保障磁流变阻尼器的性能。因此,选择天棚阻尼系数为6 000 N·s/m。
现将被动控制、天棚控制与改进复合天棚控制进行比较,检验其优化效果。将上述3组模型迭代仿真,输出结果如图18~图20所示。
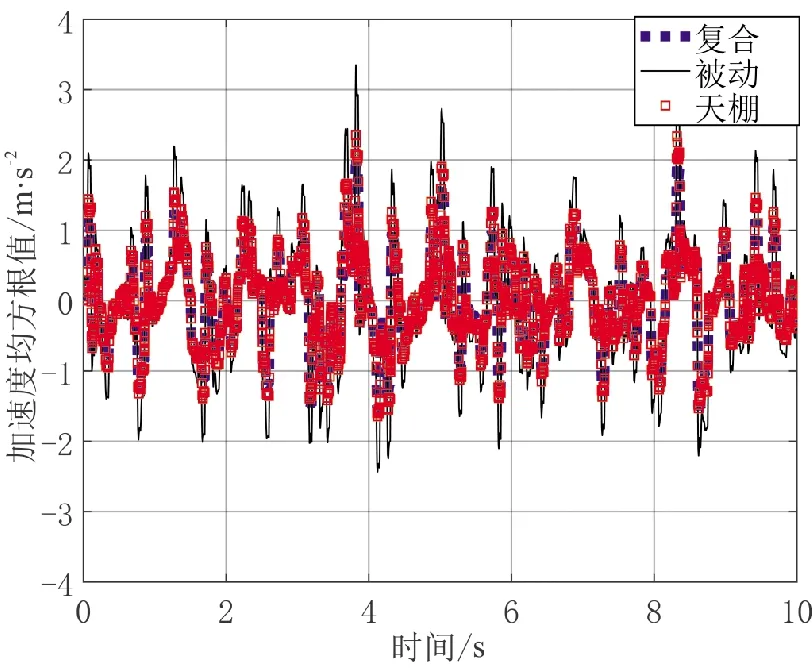
图18 不同控制算法的加速度均方根值Fig.18 RMS value of acceleration of different control algorithms
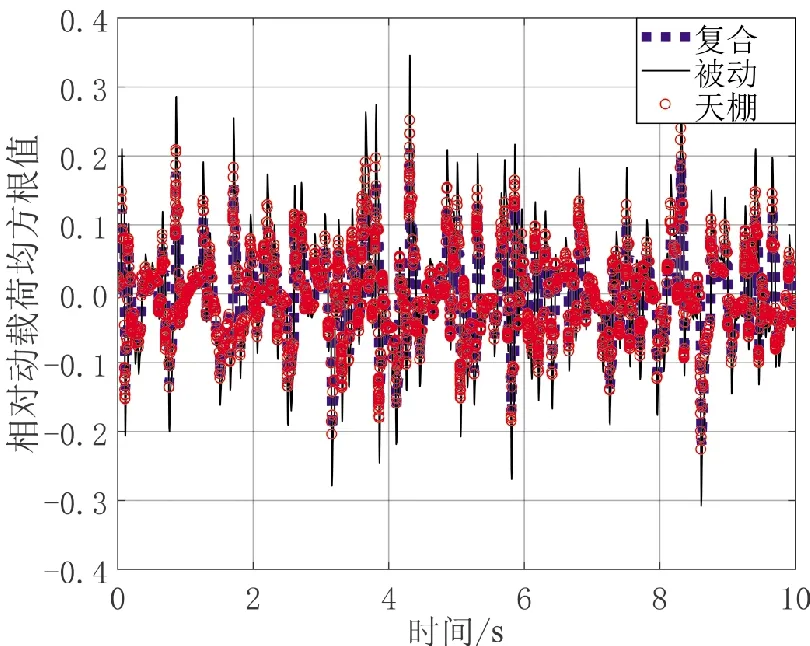
图19 不同控制算法的相对动载荷均方根值Fig.19 RMS value of relative dynamic loads of different control algorithms
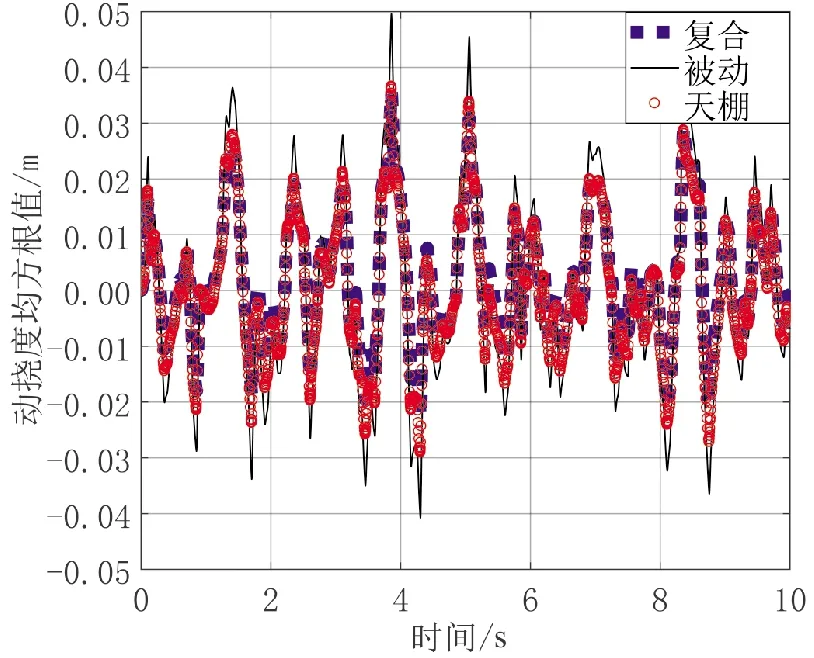
图20 不同控制策略动挠度均方根值Fig.20 RMS value of dynamic deflection of different control algorithms
从图18~图20可以看出,被动控制的加速度与动挠度处于最高水平;天棚控制在相对动载荷均方根值上略微优于被动控制,表明天棚控制无法有效地抑制轮胎跳动;优化后的改进天棚控制有效改善了机体滑跑过程的平顺性。
表2为不同控制算法的仿真结果。 相比于被动控制, 天棚控制能有效降低机体加速度均方根值与动挠度均方根值, 但对相对动载荷均方根值的抑制效果不明显; 相比于被动控制, 改进复合天棚控制能有效提升机体滑跑过程平顺性, 3个相关性能指标均得到有效改善。 改进的复合天棚控制算法的加速度均方根值较被动控制加速度均方根值减少40.45%, 相对动载荷均方根值减少11.91%,动挠度均方根值减少15.38%。因此,改进的复合天棚控制不仅降低了机体滑跑过程加速度均方根值,且在一定程度上提升滑跑过程操纵稳定性,克服传统天棚控制无法有效抑制轮胎跳动进而导致相对动载荷偏高的缺陷。尽管由于阻尼系数限制,动挠度未能达到预期优化效果,但相比被动控制也达到一定程度的优化。该复合天棚控制策略非常适用于飞机滑跑过程减震器的半主动控制。

表2 仿真结果汇总Tab.2 Summary of simulation results
5 结语
1)基于Matlab Simulink平台,针对减震器不同压缩行程阻尼、复原行程阻尼进行了飞机滑跑过程运动学仿真试验,仿真结果表明,飞机传统被动式减震器过大的阻尼系数不利于改善滑跑过程的平顺性。因此,本文提出了限制阻尼系数的复合天棚控制算法,依据仿真试验结果得到限阻尼系数的区间。
2)对复合天棚阻尼控制算法的天棚阻尼系数与地棚阻尼系数进行仿真迭代优化,并结合限阻尼系数模块得到改进的复合天棚控制算法。不仅克服了传统天棚控制无法抑制轮胎跳动的缺陷,而且也解决了地棚控制动挠度值偏大的问题,为提升飞机滑跑过程操纵稳定性与舒适性提供了一种新思路。
