基于深度学习的智能学习资源推荐算法

宋菲菲，隋 栋，周湘贞

(1.内蒙古电子信息职业技术学院 计算机与网络安全学院，内蒙古 呼和浩特 010011；2.北京建筑大学 电气与信息工程学院，北京 102406；3.北京航空航天大学 计算机学院，北京 100191)

互联网数据日益增长，学习用户从网络中获取有效学习资源的难度提升。从用户端来讲，用户需要花费更多的时间来完成有价值数据的全网检索[1]。因此，主流方法是通过服务端的记录、统计和计算来实现用户的个性化资源推荐，以解决用户从海量数据快速获取价值数据的问题。当前，基于云端的在线学习得到了学习用户的青睐，但是在线环境资源量大、资源形式多样化以及资源可用平台限制等原因造成资源推送难度提升。为了实现资源精准推荐，需要细粒度地分析学习用户和所供资源的特征属性，尽量去寻找两者属性的最小差异，为用户匹配特征差异最小的资源。

当前，关于智能推荐的研究较多，温占考等[2]采用Hadoop平台对资源进行管理和推荐，借助Hadoop来完成海量资源管理与推送。冯兴杰等[3]将Spark平台用于大量资源推荐，以此来提高资源推荐的效率。前两者均是基于云计算环境海量资源的推荐研究，更侧重于云计算的数据推送平台建设，对微观的资源细节及方法未深入展开。莫恭钿等[4]和崔建双等[5]分别采用协同过滤算法和多分类支持向量机算法来构建智能推荐系统，并进行了具体实证分析，推荐准确度得到提升，但是仍无法有效体现微观的资源细节。

近期，深度学习技术在人工智能领域表现十分突出，樊海玮等[6]提出基于深度神经网络的学习资源推荐算法，对资源细节的多特征属性具有较好的识别和分类效果。因此，本文借助于深度学习算法，运用深度学习中的广义回归神经网络(Generalized regression neural network，GRNN)算法对在线教学环境的资源进行推荐。为了提高GRNN算法的资源推荐适应度，对GRNN算法进一步优化，从而更进一步提高资源推荐的准确度。

1 资源推荐

学习资源推荐问题模型包含学习者和 学习资源两个实体模型。学习资源推荐实际上是根据学习者和学习资源的多个维度之间的特征，发现两者之间特征差异最小值，进行精准匹配，推荐个性化学习资源序列的过程。考虑到在线环境下学习资源自身属性和平台特点，需要选择在线环境下用户和资源的最关键特征。关于用户和资源特征主要如表1所示[7]。

表1 用户及资源特征描述

学习的热点可以根据学习-资源次数矩阵获得，根据表1用户及资源特征，对特征进行数字编码，然后进行特征对比求差异值，可以获得6个对应的特征差异函数S i(i=1，2，…，6)，那么推荐模型目标函数为

式中:ωi表示不同差异函数对整体推荐模型的权重。

根据推荐模型目标函数，针对每一个用户，将所有可用资源特征与用户特征差异进行升序排序，选择排名靠前的资源生成候选资源推荐序列。

2 深度学习算法极其优化

2.1 广义回归神经网络

GRNN是一个包含4层结构的神经网络结构，相比于普通神经网络，GRNN增加了求和层[8]，其主要结构如图1所示。

图1 GRNN结构

下面对GRNN网络结构进行数学描述，其网络结构主要参数如表1所示。首先，设X=

别表示GRNN的输入和输出矩阵。

其中x ij表示第j个样本的第i个输入属性，y ij表示第j个样本的第i个输出，m表示输入属性总数，n表示样本总数，k表示输出值维度。

输入信号经过输入层，通过激活函数，获得模式层结果[9]

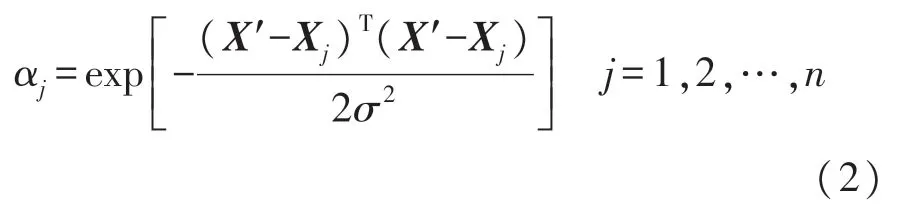
式中:σ表示平滑因子(σ＞0)，αj表示第j个模式层神经元输出，X′为任意输入的一个样本，X j为第j个训练样本。

在求和层，将所有模式层结果进行加权求和[10]

σ和核函数中心对GRNN算法的训练影响最大，引入中心偏移因子λ，以调节核函数中心位置[12]，则式(2)变为

2.2 差分进化算法的GRNN优化

上一节提到影响GRNN算法性能的主要是平滑因子σ和核函数中心偏移因子λ，在GRNN进行资源推荐时，考虑到σ和λ的设置难度，采用差分进化(Differential evolution，DE)算法对σ和λ进行优化求解，DE算法的适应度函数为GRNN资源推荐结果目标函数的倒数。下面将对DE算法进行数学描述。

设种群规模为N，属性维度为D，交叉速率C R，每个个体的取值为[Umin，Umax]，则第i个个体的j维属性可表示为

式中:i=1，2，…，N；j=1，2，…，D；rand为(0，1)随机数。

设第G代个体(i=1，2，…，N)的变异操作得到的第G＋1代个体为[13]

式中:i≠r1≠r2≠r3，r1、r2和r3为第G代中除了编号为i的个体之外随机的3个个体，F为差分缩放因子。

个体交叉方法为[14]

式中:f表示适应度函数。当达到最大代数Gmax时，DE算法停止。

F常见取值为[0，2]，DE的优化过程与F值密切相关，F值不合适将会导致差分进化算法的优化性能不高，因此在计算时引入自适应F值策略[16]

式中:Fmin和Fmax范围为[0，2]。

2.3 DE-GRNN推荐流程

首先，输入学习记录样本，然后进行用户和资源的特征数字编码，接着将特征变量输入GRNN网络，并通过DE算法进行GRNN核心参数优化，获得稳定的GRNN学习资源推荐模型，最后通过多次训练，获得稳定的DE-GRNN资源推荐模型。迭代停止的具体条件是特征差异是否满足要求，也就是说特征差异是否达到最小值，主要流程如图2所示。

图2 基于DE-GRNN的资源推荐

3 实例仿真

为了验证DE-GRNN算法在资源推荐中的性能，进行实例仿真。数据来源为某大型在线学习平台，具体样本数据见表2。为了充分验证DEGRNN的推荐性能，首先验证DE对GRNN的优化性能，分别采用GRNN和DE-GRNN算法进行推荐性能仿真，其次分别采用常用资源推荐算法和本文算法进行推荐性能仿真。

表2 仿真样本集

3.1 DE的优化性能

3.1.1 特征差异最小值性能仿真

为了验证DE算法对GRNN资源推荐的优化性能，分别采用GRNN算法和DE-GRNN算法对表2中的3个样本集进行归一化特征差异平均最小值性能仿真，以验证2种算法生成候选推荐序列的准确度。

图3～图5均反映出DE-GRNN求解的特征差异值比GRNN算法更小，对于3个样本集，DE-GRNN算法的特征差异平均最小值均不大于0.1，而GRNN算法特征差异平均最小值均大于0.15。从收敛性方面看，在样本集1的特征差异最小值求解过程中，GRNN更早完成收敛，而在样本集2和样本集3的求解过程中，GRNN和DEGRNN算法表现非常接近。横向对比发现，随着学习记录条数增多，特征差异值更小。

图3 GRNN与DE-GRNN的特征差异最小值(样本集1)

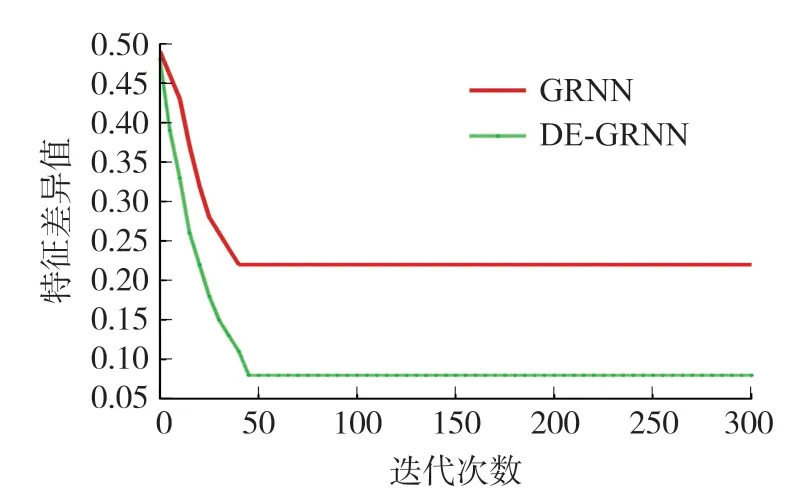
图4 GRNN与DE-GRNN的特征差异最小值(样本集2)

图5 GRNN与DE-GRNN的特征差异最小值(样本集3)

3.1.2 稳定性及效率仿真

为了进一步验证DE算法对GRNN的优化性能，对GRNN和DE-GRNN的特征差均值标准差和候选推荐序列求解时间进行性能仿真，结果如表3所示。

表3 GRNN和DE-GRNN算法的标准差及推荐时间

从表3可知，DE-GRNN的特征差异均值标准差性能明显比GRNN算法更小，其中DE-GRNN算法在样本集1的标准差性能最优，仅为0.003 2，而GRNN的最小标准差为0.004 7。从2种算法的候选推荐序列求解时间来看，学习记录条数越多，推荐耗时越长。对比发现，相同样本集，DE-GRNN算法需要更多的推荐时间，但两者运算时间差距并不大，这是因为经过DE优化后，GRNN算法能够更快获得更小的特征差异值，所以经过DE优化后，并未耗费大量计算时间。

3.2 不同算法的推荐性能

为了验证不同算法对3个样本集的资源推荐性能，分别采用协同过滤[4]、支持向量机(Support vector machine，SVM)[5]、深度神经网络[6]和DE-GRNN算法对3个样本集进行训练。对比用户实际选择的学习资源和经过4种算法推荐的候选资源序列，计算4种资源推荐系统的准确率、召回率和F1值。

从表4可知，对于3个样本集，DE-GRNN的资源推荐准确率最高，均高于0.91，深度神经网络次之，准确率都收敛于0.8以上，协同过滤和SVM表现较差，均未超过0.7；而在召回率和F1值方面，DE-GRNN算法的性能表现也高于其他3种算法。

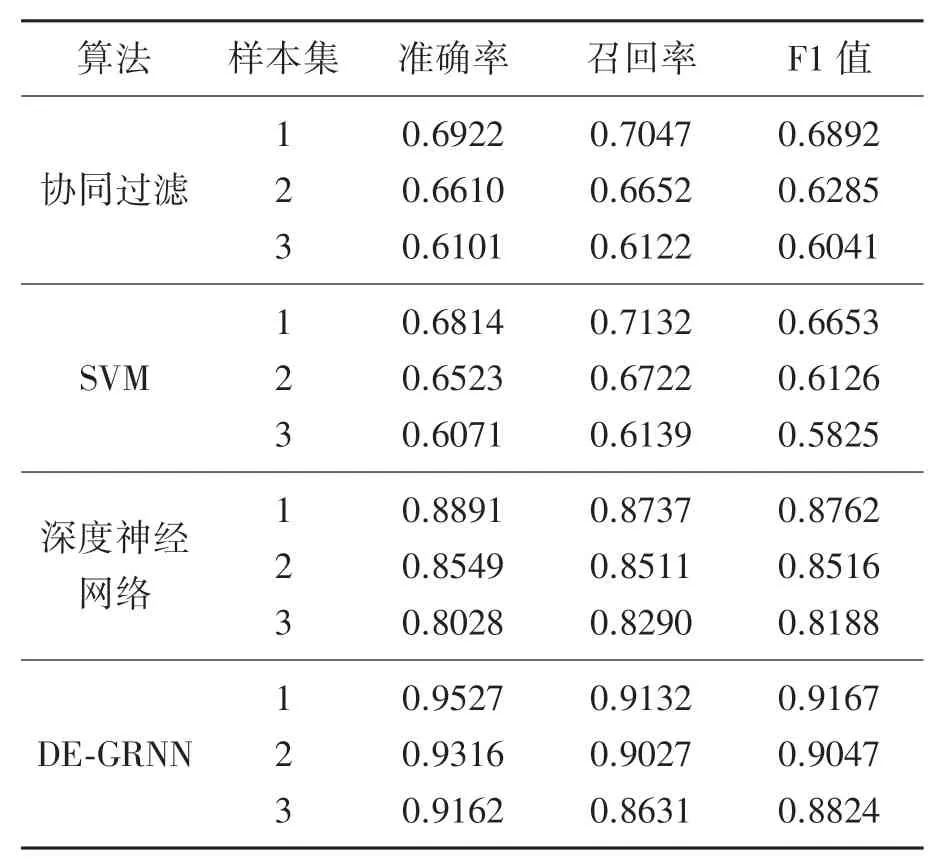
表4 4种算法的推荐性能

为了更充分地验证4种算法资源推荐准确率的稳定性，分别对3个样本集求解4种算法资源推荐准确率的均方根误差(Root mean square error，RMSE)值，其结果如图6～图8所示。

图6 4种算法的推荐准确率RMSE性能(样本集1)

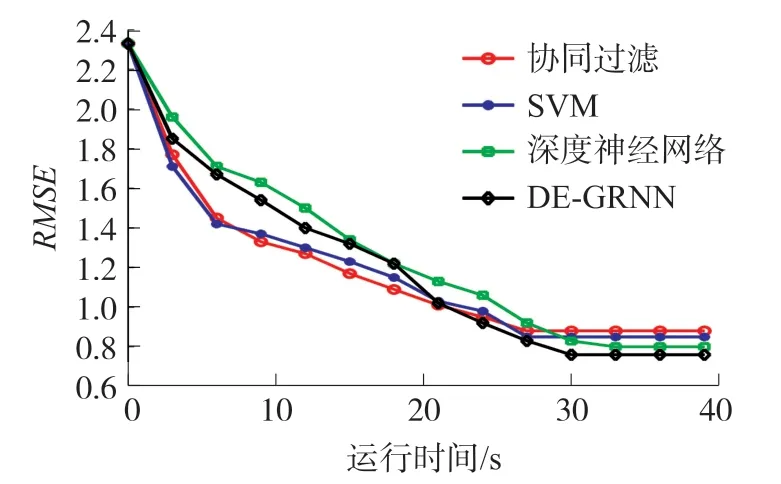
图7 4种算法的推荐准确率RMSE性能(样本集2)

图8 4种算法的推荐准确率RMSE性能(样本集3)

从图6、图7和图8可知，对于3个样本集，从推荐准确率的RMSE值方面看，DE-GRNN算法的性能最优，深度神经网络次之，协同过滤表现最差，SVM和协同过滤算法的RMSE接近。从推荐效率方面来看，协同过滤和SVM表现了更优越的性能，DE-GRNN次之，深度神经网络表现最差。

在样本2、3中，也就是学习记录条数增多时，DE-GRNN的准确率RMSE值在没稳定前都是基本高于其他对比方法的，且其稳定速度也慢于其他方法。这是因为DE-GRNN不同于其他方法，其性能受到特征差异最小值求解过程的直接影响，且当特征差异接近最小值时才能趋于稳定。

4 结束语

将广义回归神经网络应用于推荐系统，在训练样本量充足时，合理设置DE算法的交叉速率和差分缩放因子，通过DE优化，能够对GRNN算法的平滑因子和核函数中心进行优化求解，获得合适的平滑因子和核函数中心，提高GRNN算法的资源推荐性能。试验证明，相比于常见资源推荐算法，本文算法能够获得更小的用户-资源特征差异度值，学习资源推荐更精准。后续研究将进一步对GRNN核心参数更新进行优化计算，以提高GRNN推荐效率，提高这一算法在学习资源推荐中的适用度。