汽车发动机风扇悬臂转子动力学特性分析

李心怡，李正美，安琦

(华东理工大学 机械与动力工程学院，上海 200237)

汽车发动机风扇转子由皮带系统驱动，结构为悬臂方式，是一个较为复杂的转子系统。在发动机工作时，风扇转子的振动不仅会产生噪声，也会降低支承轴承寿命。故有必要对风扇悬臂转子的动力学特性进行分析。

国内外对轴承-转子动力学做了一定研究：文献[1]认为转子仅在低于1阶弯曲临界转速时才能稳定运行；文献[2]分析了预紧力及滚动体数量对滚动轴承支承的转子系统振动性能的影响，发现合理的滚动体数量和预紧力能有效减小振动幅值；文献[3]建立了角接触球轴承刚度系数与载荷、转子转速的函数关系，通过传递矩阵法分析了轴承-转子系统的动力学特性，结果表明刚度对系统动力学行为的影响显著，所提出的ALM优化设计方法有效；文献[4]以汽车发动机水泵轴承转子系统为研究对象，构建了转子支承轴承力学模型，并与传统方法所求载荷计算结果对比,认为在考虑汽车轴承设计计算时，应考虑转轴和滚子变形的影响；文献[5]以风扇-齿箱系统为研究对象进行有限元建模，优化了悬臂转子的动力学特性计算方法，最终得到了与工程实际更为接近的数值计算结果；文献[6]建立了某链式悬臂滚动轴承-转子系统的传递矩阵模型并与有限元法对比，得到了2种分析方法下悬臂转子系统动力学特性的差异；文献[7]建立了涡扇发动机风扇转子动力学模型，分析结果表明影响系数和传递函数对弹性支承的对称风扇转子振动响应会有较大影响；文献[8]对空调贯流风扇转子系统进行了离散化建模，采用改进的传递矩阵法分析了转子系统支承轴承受力及寿命，结果表明考虑与不考虑转子振动时轴承受力及寿命有明显差异；文献[9]采用拟动力学法计算角接触球轴承刚度，分析了外力、不平衡力和轴承刚度对轴承-转子系统动力学特性的影响，并给出了优化转子动态性能的方法；文献[10]建立了滚动轴承波纹度、球离心力和陀螺力矩共同作用下转子系统的有限元模型，在此基础上分析了轴承-转子系统的动态特性，研究表明轴承的几何参数会影响转子系统的振动特性；文献[11]利用传递矩阵法分析了考虑离心力及陀螺效应的角接触球轴承支承的转子系统，提出变预紧力主轴在高速下温升低于恒压预紧主轴，低速下动刚度明显提高；文献[12]采用传递矩阵法对不对称不平衡的深沟球轴承-弹性转子系统的瞬态响应进行分析，为轴承-转子系统的动力学特性提供了理论支撑；文献[13]运用传递矩阵法对变截面轴的轴承-转子系统进行建模，在此基础上提出了一种改进的传递矩阵法——直接积分法计算分析了轴承-转子系统的临界转速、不平衡响应和模态振型；文献[14]采用有限元法分析了角接触球轴承-转子系统的转速及轴系预紧量对振动频率的影响，试验表明频域信号的最大峰值处频率与轴系静频有关；文献[15]建立了离心压缩机叶轮-转子-轴承系统的动力学模型，对比分析了集中质量法和有限元法分析转子系统动力学特性的差异，同时给出了转子系统振型耦合作用影响的转速范围；文献[16]通过达朗伯原理分析了预紧量对球轴承-转子系统动力学特性的影响，得出转子系统最大振幅随预紧量增大先增大后减小的结论。

上述对各类转子进行了力学及动力学特性分析，但尚未有汽车发动机风扇悬臂转子动力学特性的研究。鉴于此，以汽车发动机风扇悬臂转子为研究对象，建立动力学模型，分析各类因素对风扇转子动力学特性的影响。

1 风扇转子力学模型

1.1 风扇悬臂转子结构

风扇悬臂转子结构如图1所示，轴承与风扇叶轮、风扇带轮、悬臂轴及主轴组成了一个悬臂转子系统。风扇带轮经皮带由汽车发动机曲轴驱动，带动主轴与悬臂轴和风扇一起旋转。当发动机温度过低时，离合器因内部硅油难以流动而分离，此时风扇不工作；温度升高时，硅油的流动使离合器与风扇结合，风扇随主轴一起旋转，转速升高。

1—硅油离合器总成；2—风扇；3—悬臂轴；4—主轴：5—风扇带轮；6—角接触球轴承；7—风扇支架；8—发动机箱体。

1.2 风扇悬臂转子力学分析

风扇悬臂转子系统受力如图2所示，风扇转子所受外部力有风扇叶片上的轴向力(轴流式风扇，无径向力)、带轮皮带拉力、风扇轴承径向载荷和轴向载荷、各零件自身重力(风扇与离合器总重力Gf(质心偏移距离Li)，带轮重力Gp，风扇轴承重力Gb，悬臂轴与带轮的紧固螺栓重力Gs，主轴螺钉重力Gr)。

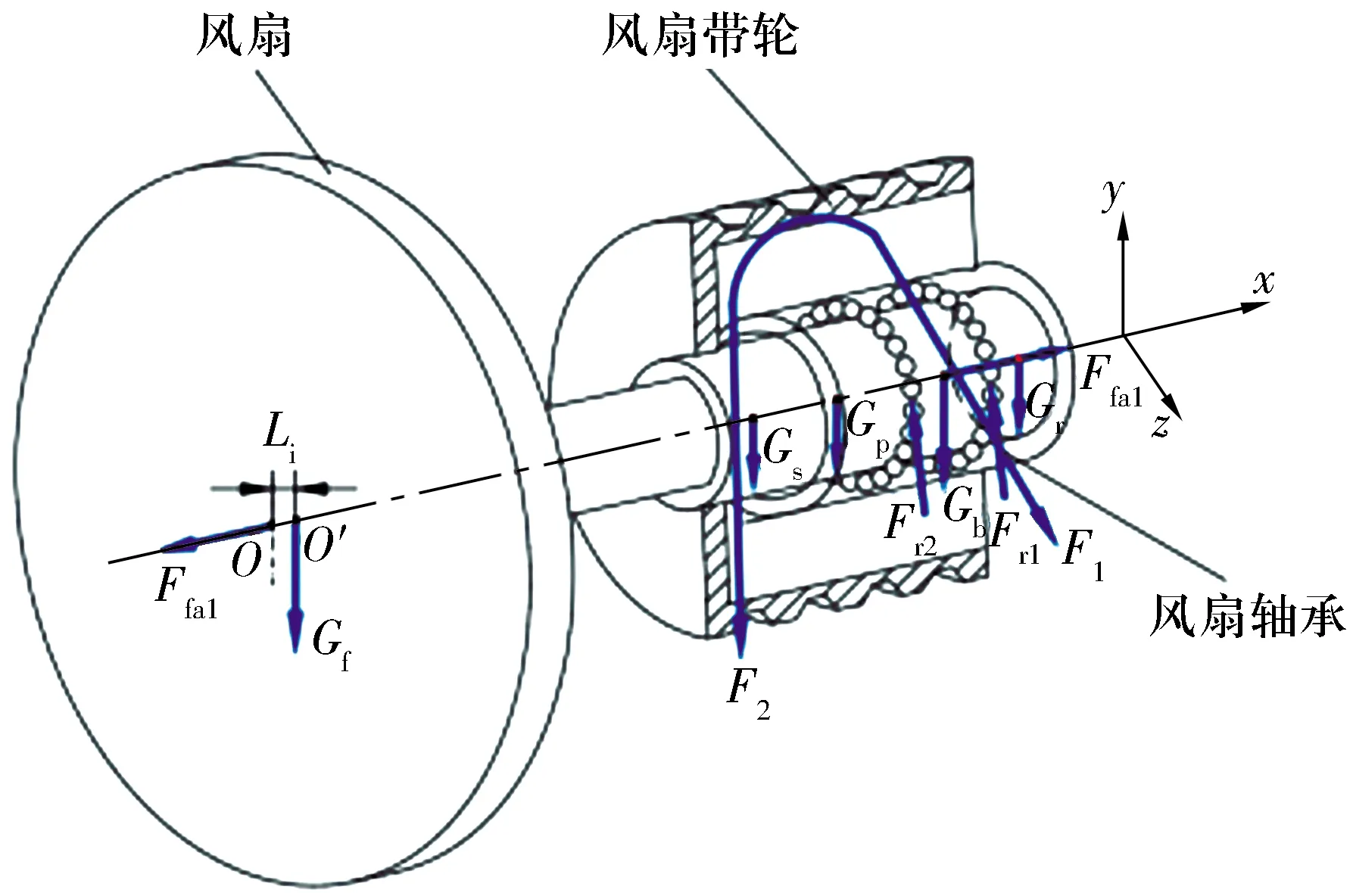
图2 风扇悬臂转子系统受力图Fig.2 Force diagram of fan cantilever rotor system

1.2.1 风扇叶片上的轴向力

风扇叶片及带轮受力如图3所示，由于轴流式风扇的叶片轴对称，可不考虑径向力。风扇叶片所受轴向力为

(1)

图3 风扇叶片结构及受力示意图Fig.3 Fan blade structure and force diagram

1.2.2 带轮皮带拉力

风扇带轮受力如图4所示，风扇传动带以一定的张紧力F0作用在带轮上，有效拉力F为

F=F1-F2,

(2)

式中：F1,F2分别为风扇带轮上的紧边和松边拉力。

图4 风扇带轮受力示意图Fig.4 Force diagram of fan pulley

皮带张紧力为

(3)

式中：μ为当量摩擦因数；α0为轮包角；q为皮带线密度；v为带速。

1.2.3 风扇轴承径向载荷和轴向载荷

汽车发动机风扇悬臂转子系统在水平和竖直平面内的受力如图5所示。

图5 转子系统受力分析图Fig.5 Force analysis diagram of rotor system

由图5可得风扇悬臂转子系统各零件之间的几何关系，在此基础上分别在水平和竖直平面内建立其力平衡方程及弯矩平衡方程，得到角接触球轴承径向力Fr1，Fr2，即

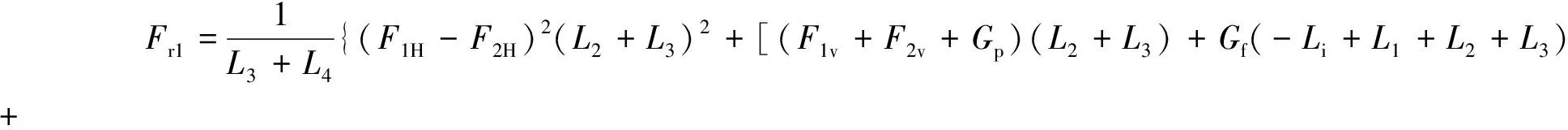
(4)

(5)

式中：F1H，F1v分别为皮带紧边拉力在水平和竖直方向的分量；F2H，F2v分别为松边拉力在水平和竖直方向的分量；L1为风扇与带轮中心距；L2为竖直拉力与轴承中心的距离；L3为带轮与轴承2中心距；L4为带轮与轴承1中心距；L6为轴承2与主轴螺钉之间的距离;Ls为螺钉到风扇中心的距离。

风扇轴承的内部派生轴向力为

(6)

式中：Y为轴向载荷系数。

1.3 转子支承轴承力学分析

冷却风扇转子支承轴承为背靠背安装的角接触球轴承，外圈固定，轴承载荷分布如图6所示，在径向力Fr、轴向力Fa和力矩Mm联合作用下轴承内外圈会产生相对移动。

图6 角接触球轴承载荷分布图

由文献[17]可得受载后球与内外圈沟道的法向接触变形δn为

δnj=l′-l=[(lcosα0+0.5dcθcosφj+

(7)

式中：l，l′分别为受载前后轴承内外圈沟曲率中心距；α0为相邻2个球的夹角；dc为轴承中心距；θ为球姿态角；φj为第j个球位置角(0°位置为受载最大球位置)；δa，δr分别为内外圈相对轴向位移和径向位移；Ri为轴承中心与内沟曲率中心的距离。

受载后第j个球对轴承的载荷为

(8)

式中：kn为载荷-位移系数。

整套轴承受力平衡方程为

(9)

式中：Fx,Fy,Fz分别为轴承在x，y，z方向所受作用力；Mx,My分别为绕x，y轴方向的作用力矩；Z为球数；Qij为球与内沟道的接触载荷；αi为球与内沟道的接触角。

轴承变形δ=[δx,δy,δz,θx,θy]T与作用力F=[Fx,Fy,Fz,Mx,My]T的关系为Kδ=F，由文献[17]可得角接触球轴承刚度K为5×5的雅可比矩阵，即

(10)

(11)

(12)

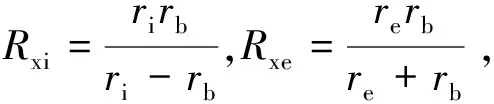
式中：a为接触椭圆长半轴；E为综合弹性模量;α为黏压系数；η0为润滑油动力黏度；n1为转速；ri，re分别为内外圈沟曲率半径；rb为球半径。

角接触球轴承综合阻尼为

(13)

2 风扇转子动力学模型

采用传递矩阵法对风扇悬臂转子进行动力学建模，转子离散化模型如图7所示，将汽车风扇悬臂转子系统离散为13个集中质量(节点)的刚性圆盘及12个无质量的弹性轴段，建立风扇悬臂转子系统始末端轴段状态变量间的传递方程，进而根据边界条件求出悬臂转子系统的临界转速和模态振型。

图7 风扇转子系统离散化模型Fig.7 Discretization model of fan rotor system

转子系统无质量弹性轴段受力如图8所示，在yOz面内第i个构件轴段两端的状态向量可用[ya,θa,Ma,Qa]T表示。假定轴段受到的轴向力为Fa1，由力学分析可得系统无质量弹性轴段左右两侧截面参数之间的传递关系为

(14)

式中：ya为轴段挠度；θa为截面角度；Ma为截面力矩；Qa为截面剪力；l为轴段长度；EI为轴抗弯刚度；上标L，R分别代表左右侧。

图8 第i个无质量轴段受力图Fig.8 Force diagram of the i th massless axial section

轴承支承的刚性圆盘处受力如图9所示，假设刚性圆盘受到q=mra(m为圆盘质量，ra为圆盘半径)的不平衡力，根据力学分析得到刚性盘横截面参数之间的传递关系为

(15)

式中：ω为圆盘转动角速度；K为轴承刚度；J为圆盘转动惯量。

图9 第i个刚性支承薄圆盘受力图Fig.9 Force diagram of the i th rigid supported thin disk

当刚性薄圆盘无弹性支承时，令(15)式中相关传递矩阵中的K和C为0可得传递关系。

将无质量弹性轴、无弹性支承薄圆盘、有弹性支承薄圆盘组合成包含轴承的第i个单元，传递矩阵为

(16)

对轴系重复的使用传递矩阵可得到如下关系

T=T13·T12·…·T3·T2·T1=

(17)

风扇转子系统边界条件为

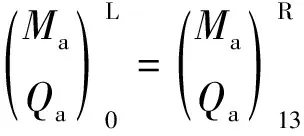
(18)

将(18)式代入传递矩阵，可得

(19)

求解(19)式可得风扇悬臂结构转子右侧支承轴承位置处的振动位移Δy和临界转速n。振动引起的风扇悬臂转子与右侧支承轴承的作用力可表示为

Fv=KaΔy，

(20)

式中：Ka为位移系数。

综上，考虑转子振动时支承轴承受到的总径向力为

(21)

基于MATLAB编程求解，通过对轴段两端传递关系推导可得转子系统振型曲线，其计算步骤如下：

1)将转子轴系离散化构成盘轴集中质量系统，输入转子的几何物理参数；

2)计算球轴承刚度和阻尼；

3)设置初始频率、步长和边界条件；

4)计算转子传递矩阵T=T13·T12·…·T2·T1；

6)判断剩余量Δω2是否等于零，若是则重复步骤4—6，若否则执行步骤7；

7)按给定的步长增加进动频率ω=ω+Δω；

8)判断进动频率是否超出给定频率范围,若是则执行步骤9，若否则重复步骤4—8;

9)判断两相邻剩余量Δω2是否异号，若是则执行步骤10，若否则重复步骤4—9;

10)利用二分法计算频率方程的根，求解临界转速n及各截面的状态向量；

11)绘制出各频率下的振型图。

3 实例分析

以某型汽车风扇发动机悬臂转子为研究对象，其支承轴承为一对背靠背安装的7312C/DB角接触球轴承，汽车风扇转子系统相关参数见表1。

汽车发动机风扇悬臂转子系统的前3阶临界转速分别为2 990，25 300，54 500 r/min，转子系统的转速-剩余量曲线和前3阶模态振型如图10、图11所示,在角接触球轴承支承处,由于轴承综合刚度的影响，转子系统振型曲线会发生变化。当转子转速达到临界转速时，悬臂转子会剧烈振动。

表1 汽车发动机风扇悬臂转子系统相关参数

图10 转子的转速-剩余量曲线图

图11 转子的前3阶模态振型Fig.11 The first three order modal shapes of rotor

悬臂转子不平衡响应的振幅随转子角速度的变化如图12所示，当悬臂转子系统转动频率接近系统固有频率时，转子轴端处的响应幅值会急剧增加，从而发生共振。汽车风扇悬臂转子工作转速应远离共振区，以避免振动时其不平衡响应幅度过大。

3.1 轴承间距对转子系统振动特性的影响

轴承间距对临界转速、系统不平衡响应振幅及系统最大振幅的影响如图13所示:1)轴承间距对1阶临界转速影响较小，2阶临界转速随轴承间距增大而增大；2)系统不平衡响应振幅随轴承间距增大而减小。故应适当增大轴承间距，从而减小转子系统的不平衡响应幅值，提高支承稳定性。

图12 在不同角速度下转子轴端的不平衡响应

图13 轴承间距对临界转速、系统不平衡响应振幅及系统最大振幅的影响

3.2 皮带张紧力对转子系统振动特性的影响

皮带张紧力对临界转速、系统不平衡响应振幅及系统最大振幅的影响如图14所示：1)转子1阶临界转速随张紧力变化不明显，2阶临界转速随张紧力增大明显减小；2)转子系统不平衡响应振幅及系统最大振幅随张紧力增大而增大。故应在保证带传动正常工作的情况下选择尽可能小的张紧力，以减小转子响应振幅。

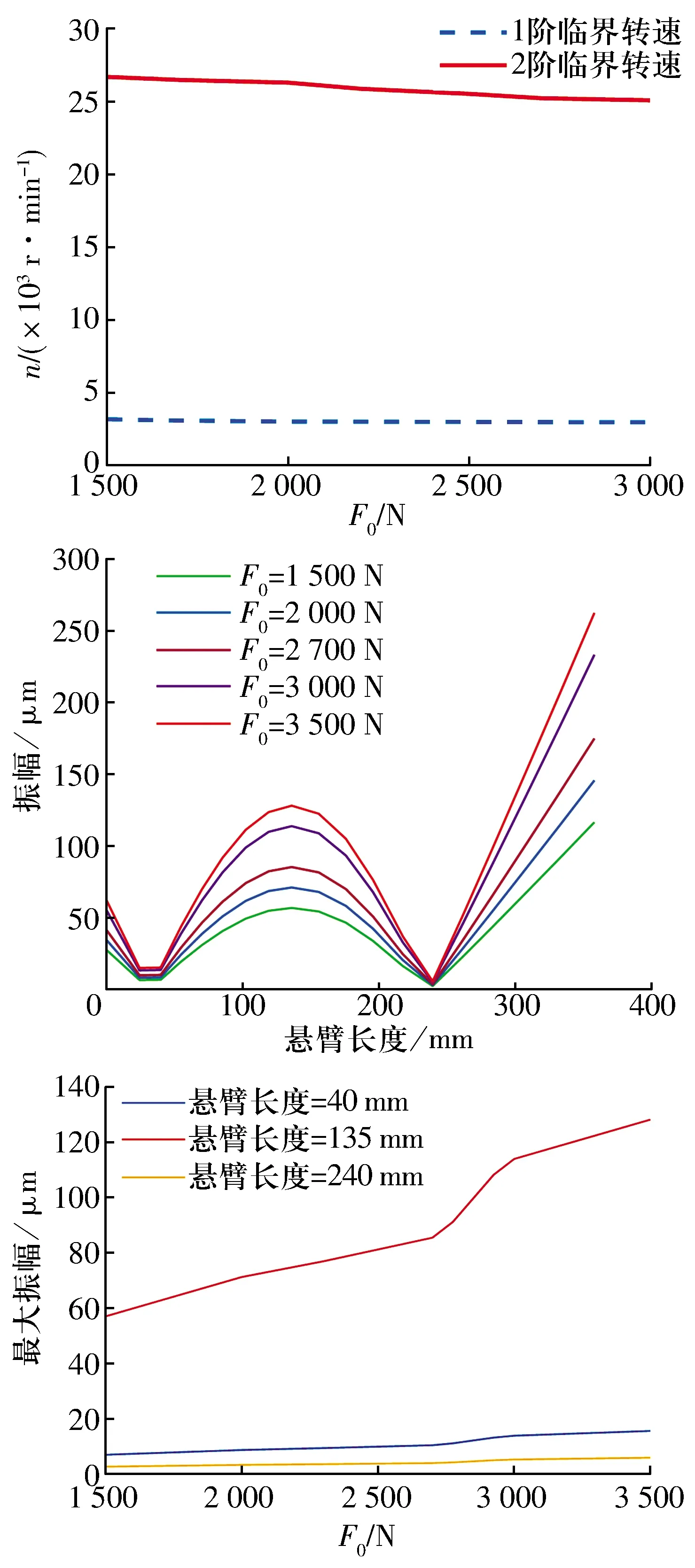
图14 张紧力对临界转速、系统不平衡响应振幅及系统最大振幅的影响

3.3 悬臂长度对转子系统振动特性的影响

悬臂长度对系统临界转速及不平衡响应的影响如图15所示:1)转子的1阶和2阶临界转速随悬臂长度增大而减小；2)最大振幅随悬臂长度增大而增大，当悬臂长度大于450 mm时，振幅会迅速上升。故悬臂转子系统的悬臂长度不宜过大。

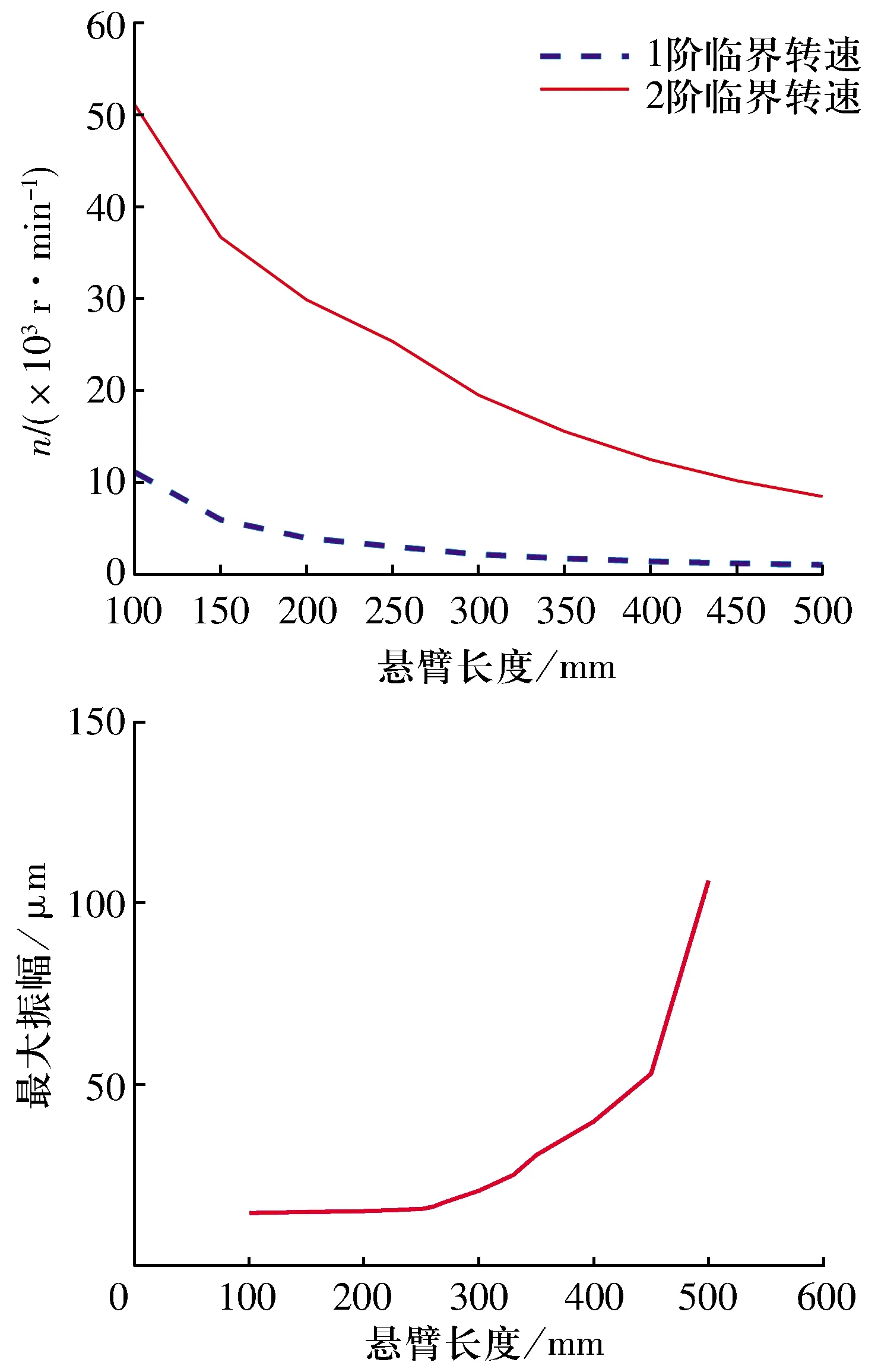
图15 悬臂长度对临界转速及不平衡响应的影响

3.4 转速对转子系统振动特性的影响

转速对悬臂转子系统不平衡响应最大振幅的影响如图16所示，随着风扇悬臂转子转速的增大，

图16 转速对不平衡响应最大振幅的影响

转子不平衡响应最大振幅减小,这表明适当提高轴转速有利于抑制悬臂转子系统的不平衡响应。

4 结论

对风扇悬臂转子系统和支承轴承进行力学分析，采用改进的传递矩阵法对风扇悬臂转子进行动力学建模，并运用数值迭代法求解。分析轴承间距、带轮张紧力、悬臂长度、转速对风扇悬臂转子系统临界转速和不平衡响应的影响，得出结论：

1)转子系统1阶临界转速随轴承间距和带轮张紧力变化不明显，2阶临界转速随轴承间距增大而增大，随带轮张紧力增大而减小；

2)1阶和2阶临界转速随悬臂长度增大而明显减小；

3)转子系统的不平衡响应振幅随轴承间距增大而减小，随带轮张紧力增大而增大。

4)转子系统的最大振幅随悬臂长度的增大而增大，随转速增大而减小。