基于等效电路和点电流源的潜艇水下腐蚀电场估算
2022-06-08赵玉龙刘春阳
赵玉龙,刘春阳,周 丹
(国防科技大学 信息通信学院, 湖北 武汉 430010)
随着潜艇服役时间的增长,潜艇表面的消声瓦或防腐涂层往往会发生局部破损甚至脱落,涂层破损部位与裸露的螺旋桨在海水中形成原电池,会使涂层破损表面腐蚀非常剧烈,不仅影响潜艇的结构强度,威胁潜艇航行安全,其在海水中产生的电流还会产生腐蚀电场,增加潜艇被敌方探测的可能性[1-3]。因此有必要分析潜艇涂层破损状态下的水下电场分布规律,对涂层破损状态下的潜艇腐蚀电场强度进行评估。
由于潜艇表面结构的复杂性,利用解析法直接求解潜艇表面的电流分布非常困难。虽然有限元法、边界元法等数值方法可以求解出复杂结构的潜艇表面电流分布,但是要进行复杂的网格剖分,且计算量非常大[4-8]。实际情况中,涂层完好部位近似绝缘,腐蚀电流近似为零,而涂层破损处的面积相对于整个潜艇表面而言较小,当螺旋桨和涂层破损区域等效半径相对于场点到潜艇的距离可以忽略时,可将螺旋桨和涂层破损区域视为点电流源,对海水环境中潜艇水下腐蚀电场进行快速估算。
1 潜艇涂层破损腐蚀电流计算
1.1 潜艇腐蚀电流产生机理
海水中含有大量可溶性盐,具有强烈的腐蚀性。而潜艇的结构部件主要是金属材料,不同金属材料在海水中具有不同的腐蚀电位,不同电位的金属发生电连接将形成原电池系统。由混合电位原理可知:当原电池系统达到稳定状态时,不同的金属具有相同的电极电位,即混合电位,且形成稳定的腐蚀电流,从而产生腐蚀稳恒电场[9]。潜艇的艇壳材料为低合金钢,而螺旋桨材料为镍铝青铜,铜质螺旋桨比钢质船壳具有更高的腐蚀电位,钢质船壳和铜质螺旋桨由大轴连接。因此,当艇体表面防腐涂层发生破损时,钢制艇体和铜质螺旋桨在海水电解质中将会发生电偶腐蚀,艇体、螺旋桨、海水形成原电池,电极电位较低的艇壳为阳极,电极电位较高的螺旋桨为阴极,形成螺旋桨—连接轴—内电阻—艇体涂层破损处—海水—螺旋桨电流回路,如图1所示。
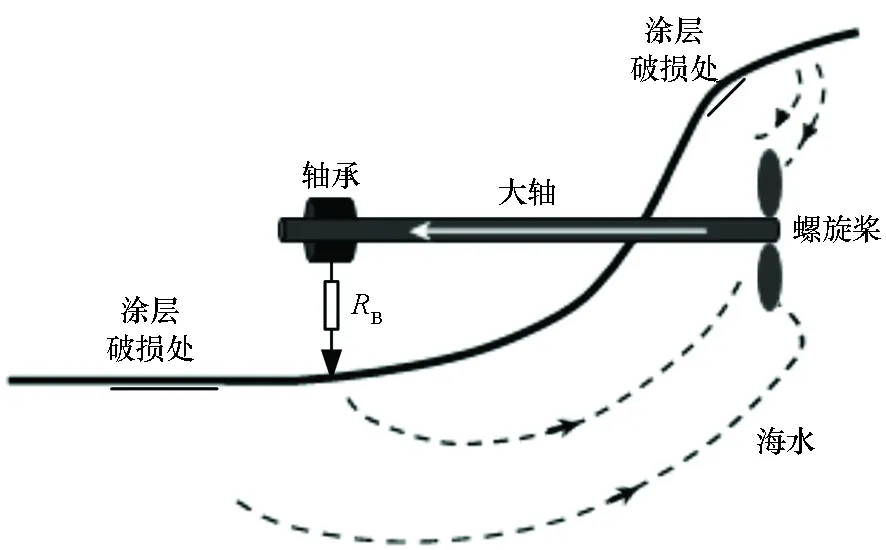
图1 潜艇涂层破损时腐蚀电流回路示意Fig.1 Schematic diagram of self-corrosive current loop for submarine coating damage
外加电流阴极保护(impressed current cathodic protection, ICCP)关闭时,在潜艇外部,电流从艇体经由海水流向螺旋桨,由于海水中有电流存在,因此海水中会产生电势差,从而形成水下电场。腐蚀电流不断从艇壳流向螺旋桨,导致艇壳涂层破损处腐蚀剧烈,并产生恒定的电场。
1.2 潜艇腐蚀电流强度估算
理想涂层状态下,涂层完好部位完全绝缘,其表面腐蚀电流为零。当潜艇表面涂层局部破损时,涂层破损处和螺旋桨之间的腐蚀电流是潜艇腐蚀电场的主要来源,若能计算出涂层破损处和螺旋桨之间的腐蚀电流,当涂层破损处和螺旋桨的几何形状相对于场点到潜艇的距离可以忽略时,可以进一步将涂层破损处和螺旋桨合理等效为若干个点电流源,根据点电流源在深海环境和浅海环境的电位表达式和电场表达式可以对潜艇的腐蚀电场进行快速估算。
1.2.1 潜艇腐蚀电流等效电路
自然腐蚀状态下(ICCP系统关闭)艇体涂层破损处、螺旋桨、大轴之间的等效电流回路如图2所示。
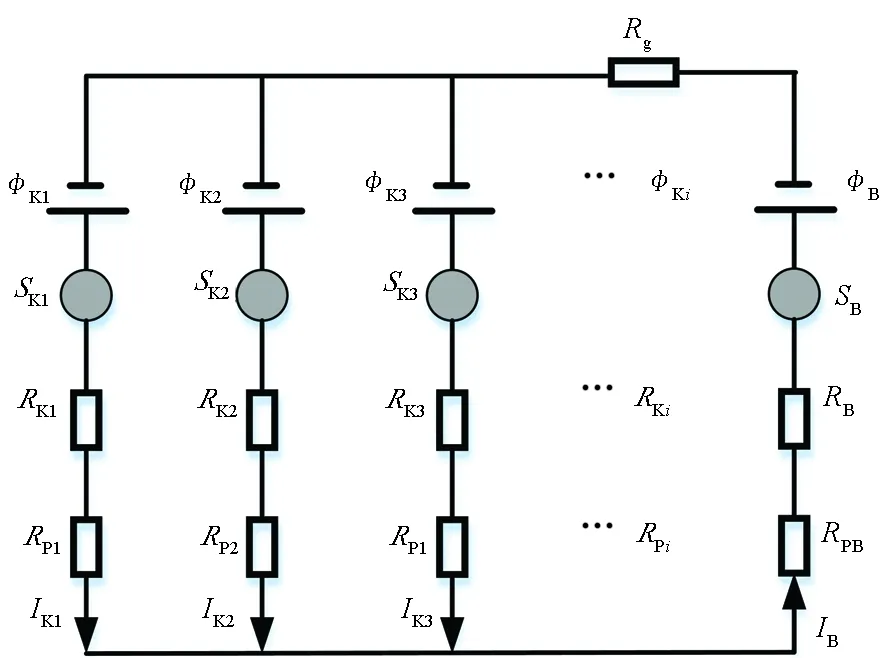
图2 潜艇腐蚀回路等效电路Fig.2 Submarine corrosion equivalent circuit
图2中,φKi为第i个涂层破损区域的自腐蚀电位,φB为螺旋桨自腐蚀电位,RKi和RB分别为艇体涂层破损处和螺旋桨的等效极化电阻,RPi为第i个涂层破损处的等效接水电阻,RPB为螺旋桨的等效接水电阻,Rg为大轴和艇体之间的内部等效接触电阻。
假设涂层破损处和螺旋桨发生电偶腐蚀后的混合电位为φ,由图2可知,第i个涂层破损处的电流强度为:
(1)
通过螺旋桨的电流强度为:
(2)
(3)
(4)
其中:PKi和PB分别为艇壳和螺旋桨金属材料的电化学极化率,即裸露艇壳和螺旋桨材料在海水中的单位面积等效极化电阻,单位为Ω·m2;SKi和SB分别为艇体涂层破损处的面积和螺旋桨水下部分的面积。由电流守恒定律可知,从涂层破损处流出的电流等于螺旋桨吸收的电流,即:
(5)
式(5)等价于:
(6)
利用式(6)求得混合电位φ后,便可利用式(1)和式(2)求解每个涂层破损区域和螺旋桨的腐蚀电流。
1.2.2 接水电阻
涂层破损处和螺旋桨的接水电阻不仅与涂层破损面积和形状有关,还与实际涂层破损位置有关,很难进行准确的计算,在计算接水电阻时,可将涂层破损处和螺旋桨等效为半球状点电极,采用文献[10]中的经验公式进行估算。
(7)
(8)
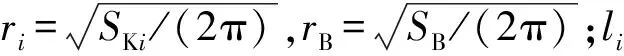
1.2.3 内部电阻
螺旋桨和艇壳通过大轴连接,潜艇的实际轴系结构非常复杂,但影响大轴与艇体之间电阻的主要是前轴承、后轴承、轴接地装置、推力轴承等与艇体的接触电阻[10],潜艇轴系的简化结构如图3所示。
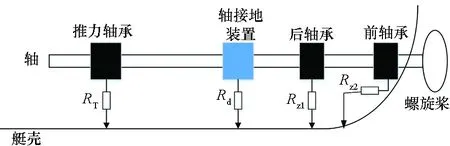
图3 潜艇轴系简化示意Fig.3 Simplified sketch of submarine shafting
潜艇轴系为低合金钢,可视为理想导体,忽略大轴自身电阻以及螺旋桨和大轴的接阻。则潜艇的轴地(壳)电阻为:
(9)
式中碳刷电阻的量级远小于轴承电阻和推力电阻,因此轴壳电阻主要由碳刷电阻决定,即Rg≈Rd,为mΩ量级[11]。
1.2.4 极化电阻
金属电极的极化电阻可由其极化曲线得到,计算腐蚀电场问题时对极化电阻有三种处理方式:第一种是忽略极化作用[4],即认为金属界面的电极反应非常快,极化电流全部用于电极反应,不同极化电流密度时,双电层电位即电极电位不发生改变,此时极化电阻为零。第二种是在研究的范围内,采用线性极化曲线,即用一条直线对极化曲线进行拟合[6,10],将极化电阻当作一个定值。第三种是采用实测极化曲线来表示极化过程[7-8],金属电极处于不同电极电位时具有不同的极化电阻。考虑到计算精度和计算量,采用线性极化曲线,即将潜艇材料的极化特性用固定的极化电阻率表示,如图4所示。
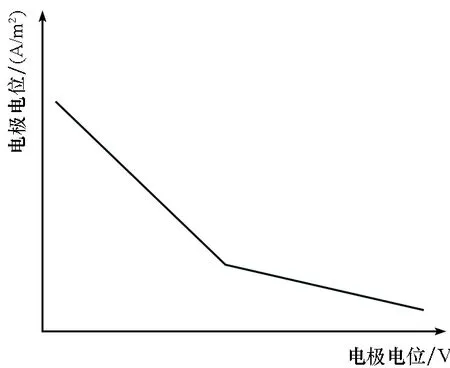
图4 线性极化曲线Fig.4 Linear polarization curve
2 基于点电流源的潜艇腐蚀电场建模
若将潜艇水下表面γ划分为n个小面源,当场点到源点的距离相对于小面源的等效半径足够大时,可将每个小面源的腐蚀电流等效为点电流源,定义点电流源的正方向为电流流入海水方向,负方向为电流从海水流出方向,潜艇在海水中产生的电位和电场为潜艇表面n个点电流源产生的电位和电场值之和。在浅海区域,海水-海床界面对点电流源的电场分布影响不可忽略,浅海区域应等效为空气-海水-海床三层模型,如图5所示。以z=0为空气和海水的分界面,z<0的空间表示空气,海水占据0
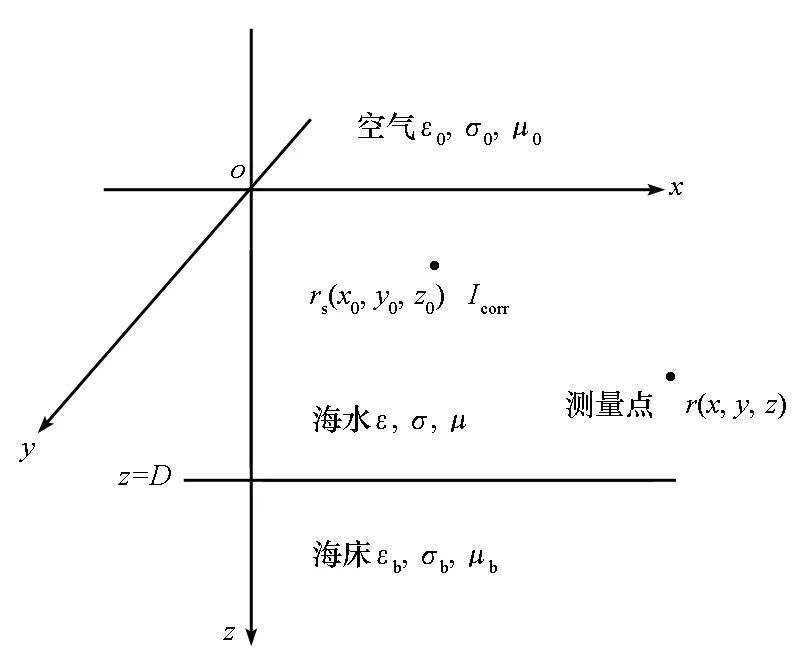
图5 空气-海水-海床三层模型点电流源示意图Fig.5 Diagram of point current source for air-sea-seabed three-layer model
点电流源在海水中的电场可看作无穷多个镜像点电流源的叠加,因此位于海水中(x0j,y0j,z0j)处的点电流源Icorr(rsj)在海水中场点(x,y,z)产生的电位表达式[12]为:
(10)
(11)
其中,r1jk、r2jk、r3jk、r4jk为点电流源Icorr(rsj)和其镜像点电流源与海水中场点之间的距离,c=(σ-σb)/(σ+σb)为反射系数。
由叠加定理可知潜艇在浅海环境的腐蚀电流产生的水下电位为:
(12)
根据E(r)=-∇φ(r)可求出浅海环境中潜艇在海水中产生的电场各方向分量。
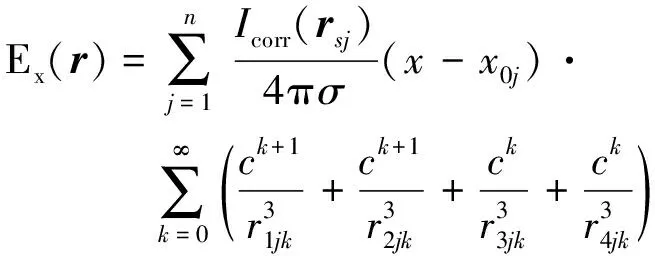
(13)
(14)
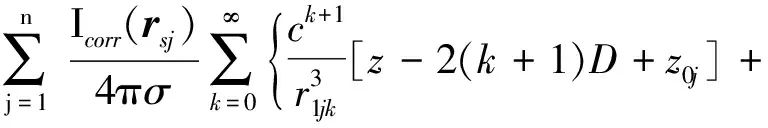
(15)
因此只要求出每个面源等效点电流源的等效位置和电流强度,就可以根据式(13)~(15)求出潜艇在浅海状态下场点处的腐蚀电位和腐蚀稳恒电场。
实际情况中,涂层电阻率远大于艇壳和螺旋桨金属材料的电化学极化率,涂层完好部位相对于涂层破损处近似绝缘,腐蚀电流可忽略不计。涂层破损处的面积一般远小于整个潜艇表面的面积,影响潜艇腐蚀电流和腐蚀电场的主要因素是涂层破损处的位置,涂层破损处的形状对潜艇腐蚀电流和腐蚀电场的影响较小。对于场点到潜艇的距离远大于螺旋桨和涂层破损区域等效半径的远场区域,螺旋桨和涂层破损区域可等效为点电流源。将涂层破损处和螺旋桨的等效几何中心和根据第2节求解得到的腐蚀电流代入式(13)~(15),就能快速解出浅海环境中的潜艇腐蚀电场。
3 潜艇腐蚀稳恒电场估算实例
3.1 潜艇模型参数与电场数据
由于边界元法、有限元法[13-15]已被广泛应用于舰艇腐蚀电场的计算,且精度较高,因此本文利用商业有限元软件COMSOL对潜艇自腐蚀状态下的电场分布进行仿真,并对潜艇腐蚀电场进行估算,利用有限元仿真结果验证本文方法对潜艇腐蚀相关电场进行估算的有效性。
潜艇有限元模型如图6所示,以空气-海水界面为xoy平面,x轴正方向由艇首指向艇尾,y轴正方向由右舷指向左舷,z轴正方向垂直向下,以艇首在xoy平面的投影点为原点o建立直角坐标系。用COMSOL建立潜艇三维模型,潜艇仿真模型包括艇壳、指挥围壳、尾舵、螺旋桨、大轴。其中: 艇体浸水面积SK为2 489.9 m2,螺旋桨面积SB为24.78 m2;艇壳材料采用低合金钢,表面涂有防腐涂层;螺旋桨裸露,材料为铝青铜;大轴和艇体之间采用铜石墨碳刷-铜基滑环连接;艇体和螺旋桨之间的内电阻为15 mΩ。涂层完好区域采用绝缘边界条件,螺旋桨和涂层破损区域用线性极化边界条件,外加长宽高分别为900 m、600 m、100 m的长方体表示海水区域。
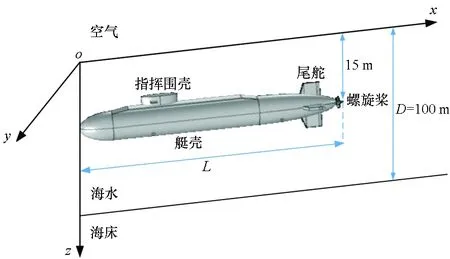
图6 潜艇有限元模型Fig.6 Finite element model of submarine
艇壳材料腐蚀电位φK=-0.69 V,阳极极化率PKa=1.5 Ω·m2,阴极极化率PKc=27 Ω·m2,螺旋桨腐蚀电位φB=-0.369 V,螺旋桨阴极极化率pBc=0.23 Ω·m2,视艇体涂层完好部位为绝缘,即法向电流为零。海水电导率σ=4 S/m,海水深度为100 m。由于海床的高阻特性,泥沙底质的海床沉积物电导率实际与海水差别不大,略低于海水,因此忽略表层海洋沉积物的影响,将其等效为海水部分,而将整个海床视为高阻体,并假设海床电导率为零,潜艇处于潜水状态,下潜深度为15 m。潜艇前部和中后部各有一个涂层破损区域,涂层破损率为2.9%,涂层破损位置和螺旋桨的面积以及几何中心见表1。
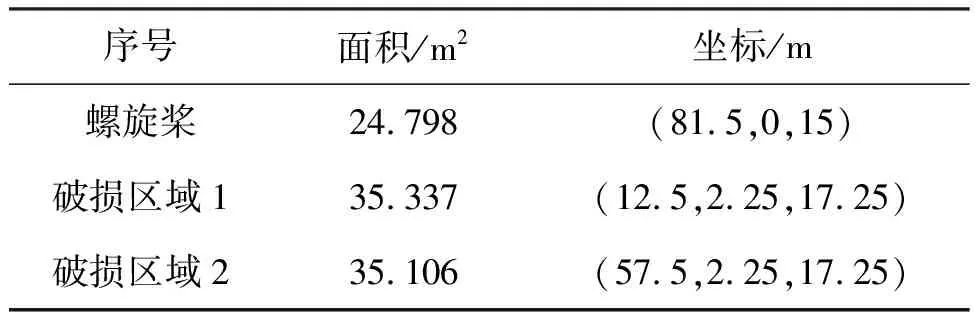
表1 潜艇破损区域面积和中心坐标
利用COMSOL二次电流模块[14]计算得到的潜艇自腐蚀状态下水深为30 m和40 m的平面电场各方向分量分布云图分别如图7和图8所示。
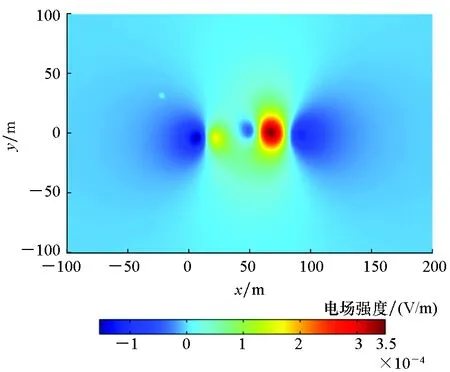
(a) Ex分布云图(a) Distribution of the Ex
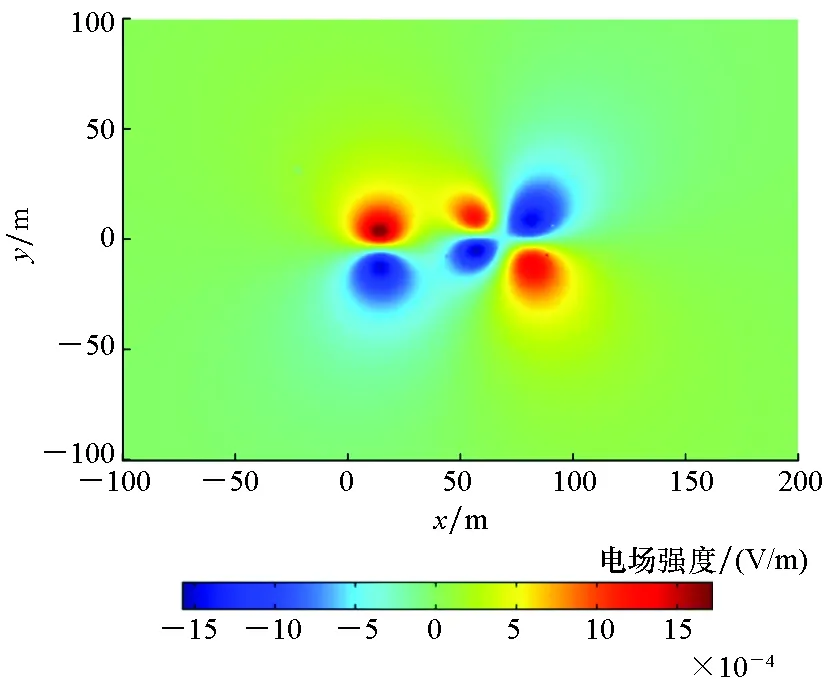
(b) Ey分布云图(b) Distribution of the Ey
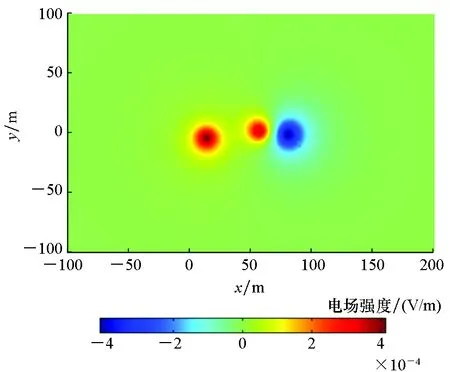
(c) Ez分布云图(c) Distribution of the Ez图7 潜艇腐蚀电场有限元计算值(z=30 m)Fig.7 Finite element calculation of corrosion electric field for submarine (z=30 m)
由图7可知,在水深30 m的平面上,潜艇腐蚀电场Ex分量和Ey分量、Ez分量的峰值仍能达到10-4V/m。Ex分量波峰波谷基本出现在潜艇
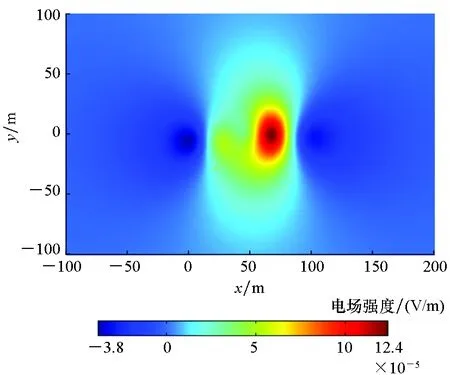
(a) Ex分布云图(a) Distribution of the Ex
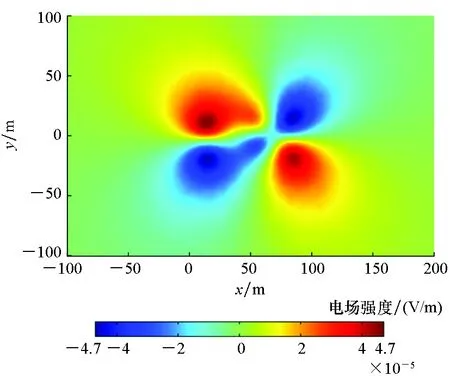
(b) Ey分布云图(b) Distribution of the Ey

(c) Ez分布云图(c) Distribution of the Ez图8 潜艇腐蚀电场有限元计算值(z=40 m)Fig.8 Finite element calculation of corrosion electric field for submarine(z=40 m)
正下方;而Ey分量的波峰波谷出现在潜艇两侧;Ez分量的正峰值和负峰值出现在涂层破损处和螺旋桨下方附近,这说明了涂层破损区域对潜艇电场分布影响较大。
由图8可知,在水深40 m的平面上潜艇腐蚀电场Ex分量、Ey分量和Ez分量的峰值相对于水深30 m时明显减小,且在水平方向的衰减速度明显小于水深30 m的衰减速度,分布特征明显。
3.2 估算结果与分析
3.2.1 电流估算结果与分析
将3.1节潜艇各项参数代入2.2节可求得图6中潜艇各个涂层破损区域和螺旋桨的腐蚀电流,在求得涂层破损区域和螺旋桨的腐蚀电流后,将涂层破损区域和螺旋桨等效为点电流源,利用叠加定理即实现对潜艇水下电场的估算。
将各部分电阻值代入式(6)可求得混合电位φ≈-0.56 V,进一步可求得破损处1、2以及螺旋桨的腐蚀电流。潜艇腐蚀电流等效电路估算结果以及COMSOL仿真结果见表2。
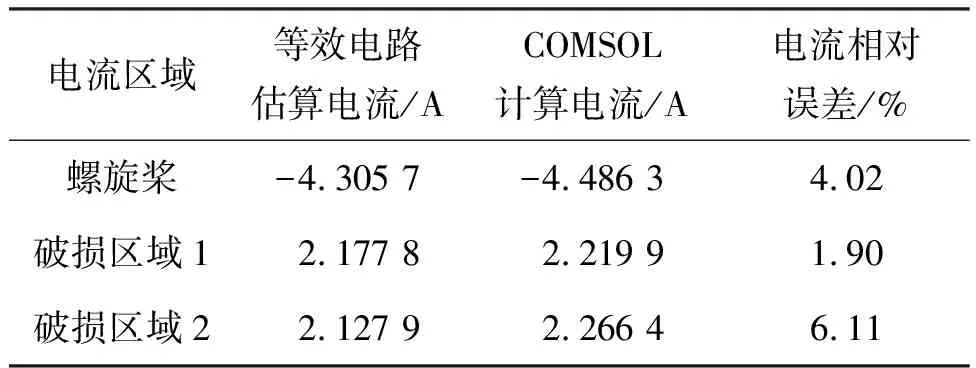
表2 电流估算结果及误差
由表2可知,采用等效电路计算得到的潜艇螺旋桨和涂层破损处的腐蚀电流与COMSOL仿真结果较为接近,估算结果略低于COMSOL有限元计算结果,但电流计算值最大相对误差均不超过6.5%,计算精度较高。
3.2.2 电场估算结果与分析
将螺旋桨与涂层破损处等效坐标和电流值代入式(17)~(19)可求出潜艇的水下电场分布。由于篇幅有限,只给出在x的范围为[-100,150] m、y=15 m、z=30 m的路径上电场各分量估算值与COMSOL仿真值对比曲线,如图9所示。由图9可知,自腐蚀状态下,利用等效电路和点电流源建模估算得到的潜艇腐蚀电场各分量与有限元软件COMSOL仿真结果具有相似的变化趋势,且幅度相当,吻合度较高。
对潜艇腐蚀电场进行估算的主要目的是对其水下电场分布曲线的峰峰值进行评估,因此定义估算结果电场各分量峰峰值与COMSOL仿真结果电场各分量峰峰值相对误差来定量分析估算误差。
(16)
式中:(Emax-Emin)c表示利用COMSOL仿真得到的潜艇某路径上的电场峰峰值,(Emax-Emin)g表示利用等效电路和点电流源模型估算得到的对应路径上的电场峰峰值。在x的范围为[-100,150]m,潜艇左右舷两侧,深度分别为z=30 m和z=40 m的路径上电场各分量估算值与COMSOL计算值的峰峰值相对误差见表3。
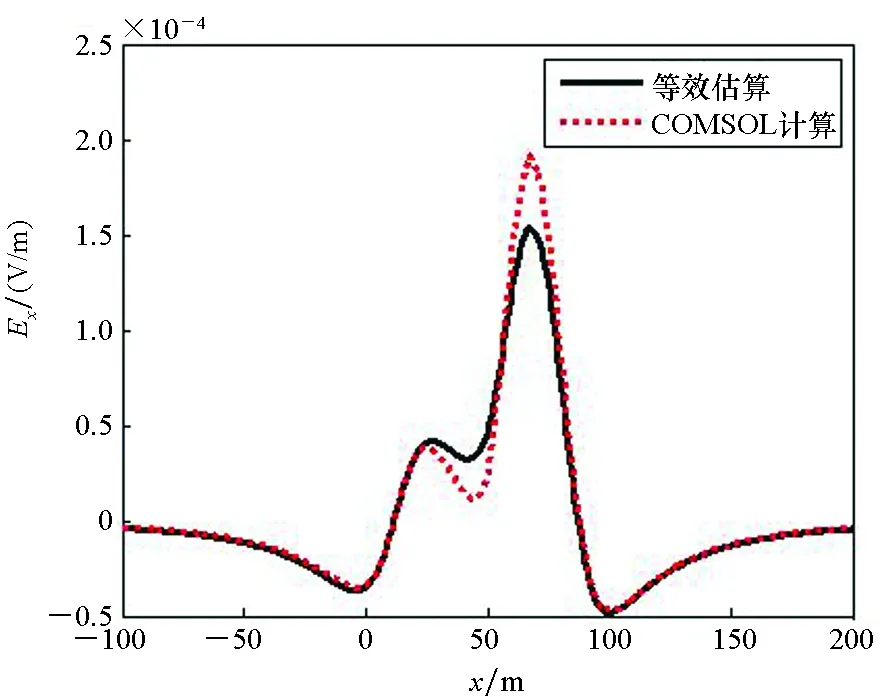
(a) Ex
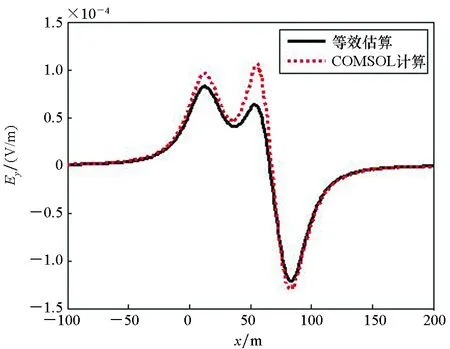
(b) Ey
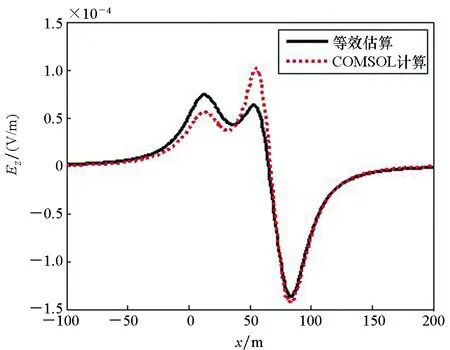
(c) Ez图9 潜艇y=15 m, z=30 m路径上电场估算值与仿真值Fig.9 Comparison of the estimated and simulation values of submarine(y=15 m, z=30 m)
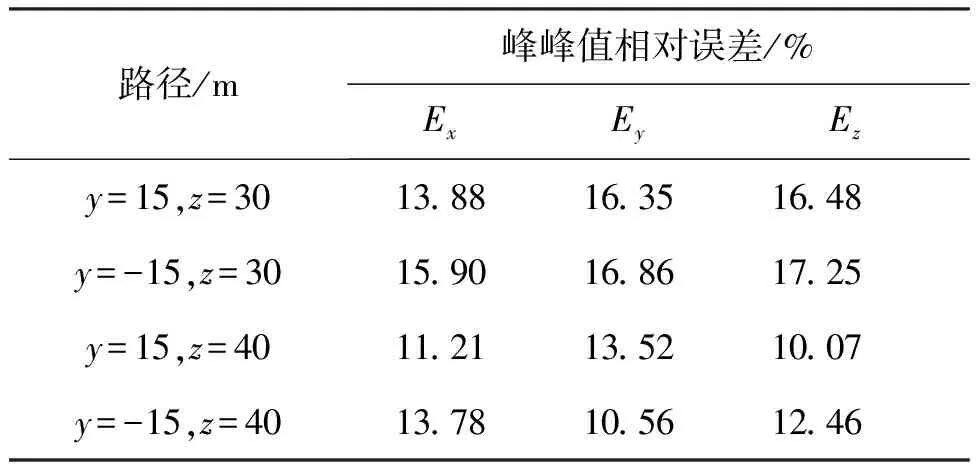
表3 电场计算误差
由表3可知,在30 m和40 m的深度上,潜艇左右舷路径上的电场各分量峰峰值相对误差均小于18%,说明在涂层状态已知情况下本文估算方法能较为有效地估算潜艇水下腐蚀电场。
3.2.3 点电流源模型误差分析
基于等效电路和点电流源模型对潜艇腐蚀电场进行估算产生的误差具有累积效应。由表2可知,利用等效电路模型对潜艇腐蚀电流进行估算的误差不超过6.5%,为了分析点电流源模型对腐蚀电场估算结果的影响,将COMSOL仿真得到的潜艇螺旋桨和涂层破损处腐蚀电流作为等效点电流源电流,利用点电源模型得到的潜艇腐蚀电场值和COMSOL仿真值的峰峰值相对误差见表4。
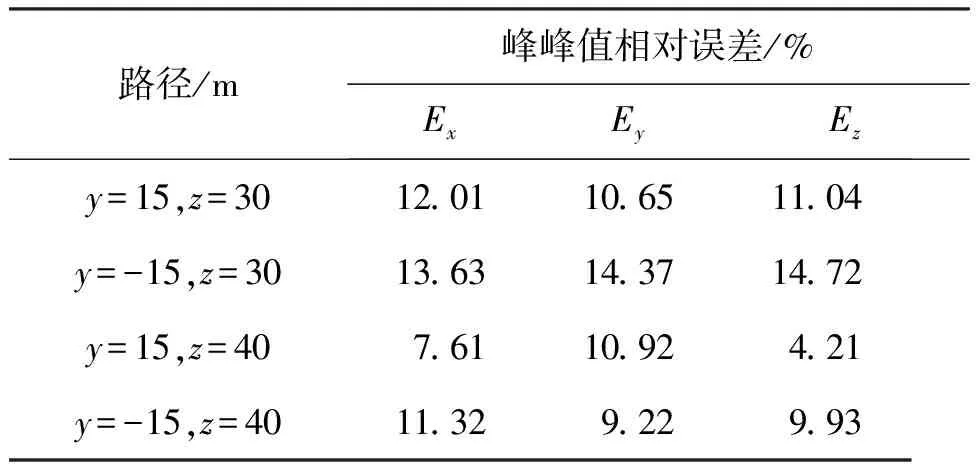
表4 点电流源模型电场计算误差
对比表3和表4可知,当不存在腐蚀电流估算误差时,利用点电流源模型对潜艇腐蚀电场建模的峰峰值精度最大能提高5.86%,接近等效电路最大电流估算误差6.5%,但最大误差仍能达到14.72%,因此点流源模型产生的误差为潜艇腐蚀电场估算主要的误差来源。
4 结论
基于等效电路和点电流源模型对潜艇腐蚀电场进行建模,并利用商业有限元仿真软件COMSOL进行仿真验证,主要结论如下:
1)不同路径电场分布曲线基本与有限元仿真结果一致,且电场各分量峰峰值相对误差和电场模最大值相对误差均不超过18%,验证了基于等效电路和点电流源对潜艇涂层破损电场估算方法的有效性和准确性。
2)基于等效电路求得的腐蚀电流略低于实际值,但最大相对误差不超过6.5%;当腐蚀电流无误差时,利用点电流源对潜艇腐蚀电场建模的最大误差为14.72%,点电流源模型产生的误差是潜艇电场估算的主要误差来源。
