基于云模型相似性度量的结构不确定性损伤识别

2022-06-08骆勇鹏郑金铃刘远贵黄方林鲁四平刘景良

铁道科学与工程学报 2022年5期

骆勇鹏，郑金铃，刘远贵，黄方林，鲁四平，刘景良

(1.福建农林大学交通与土木工程学院，福建福州350002；2.福建省结构工程与防灾重点实验室(华侨大学)，福建厦门361021；3.中南大学土木工程学院，湖南长沙410075)

作为结构健康监测领域的核心部分，损伤识别一直受到广泛关注[1]。特别是基于动力特性的结构损伤识别方法，提出了基于应变模态、Hilbert-Huang法(HHT)、小波分析法和频响函数(Frequency Response Function,FRF)[2]等识别算法。其中，FRF相比其他模态参数包含的信息更加丰富，且获得较为容易，得到了广泛应用。郭恵勇等[3]提出的基于不完备频响函数的损伤识别方法解决了实际应用中无法测量结构每个测点频响函数的问题；张宇飞等[4]提出方法无需获取结构未损伤前的模态信息，通过频响函数虚部即可对结构进行损伤识别。但相关研究结果也指出该方法易受到噪声等不确定性因素的影响，造成识别结果误差大，尤其针对损伤早期以及微小损伤的情况。近几年结构损伤识别方法经历了由确定性方法到不确定性方法的发展过程[5]，对不确定性方法的研究集中于概率统计和数据融合算法2个方面。目前对基于概率统计的不确定性损伤识别方法的研究较为广泛，也取得了一定的成果，如基于贝叶斯统计推断、随机有限元反分析、统计模式识别和概率神经网络的方法[6−7]等。通常的做法是将损伤识别的确定性指标和概率统计理论相结合进行损伤识别。NIU[8]将频率响应数据和吉布斯采样器相结合，利用概率分布确定损伤存在的概率(PDE)；PADIL等[9]同样选用了频响函数，并且和人工神经网络(ANN)相结合，用主成分分析法(PCA)解决了数据量过大的问题。值得注意的是，在损伤识别中，测量噪声、建模误差等因素同时存在，相互耦合，如随机-模糊不确定性等，这些不确定性的合理描述关系到损伤识别结果的准确与否。为了更加有效地处理不确定性问题所具有的随机性和模糊性特征，李德毅等[10]在传统的概率统计和模糊理论的基础上提出了云模型的概念，通过近几年的发展，云模型理论已广泛运用于网络、机械、土木工程等领域，并取得了良好的效果[11]。郭惠勇等[12]将云模型理论应用到损伤识别领域，提出基于残余力的云推理算法，解决了输电塔等工程结构在不确定因素干扰下的损伤识别问题。通过云模型发生器可实现定性概念与定量数据与之间的转换，而建立在定性概念基础上的信息挖掘任务则需要对数据进一步进行相似性度量。张勇等[13]通过计算云滴的距离值来表示云模型间的相似性，展开了对云模型相似性度量的研究；张光卫等[14]将云模型的数字特征当作向量，利用夹角余弦来衡量云模型间的相似度问题。近几年，随着国内外学者对云模型相似性度量的不断研究，提出了精度更高、稳定性更好的度量方法[15]。结合云模型相似性度量中的期望曲线法，提出一种基于云模型相似性度量的不确定性损伤识别方法，并通过23杆桁架模型，验证所提方法的识别效果，探讨原始样本个数及噪声水平对损伤识别结果的影响，并研究在无健康工况数据条件下的识别效果。

1 基于不完备频响函数的结构损伤识别

对于一个具有n个自由度的线性体系，其结构动力学方程为

2 基于云模型相似性度量的结构不确定性损伤识别

受测量噪声、建模误差、系统时变性等不确定性因素的影响，基于不完备频响函数的损伤识别容易出现误判，尤其是不同类型的不确定性混合在一起的时候。为此，笔者将云模型相似性度量方法引入不确定性损伤识别中，提出基于云模型期望曲线和频响函数的不确定性损伤识别方法，主要包括基于云模型期望曲线的损伤位置判别和基于云模型数字特征的损伤程度识别2个部分，具体介绍如下。

2.1 基于云模型期望曲线法的损伤位置识别

云模型是一种定性定量转换的认知模型，由云滴构成，每一个云滴的生成都具有随机性，通过云模型的3个数字特征：期望Ex(Expected Value)、熵En(Entropy)和超熵He(Hyper Entropy)可表示定性概念的整体特性，记为云模型C(Ex,En,He)。

云模型期望曲线法(Expectation based on Cloud Model,ECM)，是一种借助云模型期望曲线求解2个云模型相似程度的方法。由于具有解析式的期望曲线相对于分散的云滴能够更加有效地表示数据的总体特征，采用2个云模型的期望曲线重叠面积来描述2个云模型的相似程度，可提高相似度度量的精度。若随机变量x满足：x~N(Ex,En′2)，其中En′~N(En,He2)，且En≠0，则该云模型的期望曲线表达式为

在损伤位置识别中，单元i损伤前后的损伤系数定义为rui(Exu,Enu,Heu)，rdi(Exd,End,Hed)，根据云模型的3En规则，损伤前后某单元云模型相似性度量指标与交点x(1)o和x(2)o有关，如图1所示。因此，不同工况，需要对单元云模型数据的交点分情况进行讨论，首先根据云模型期望曲线公式求解x(1)o与x(2)o，表达式如下：

图1 云模型riu(17,2,0.3)和rid(20,5,0.3)的相似度面积SFig.1 Area of similarity between two cloud models riu(17,2,0.3)and rid(20,5,0.3)

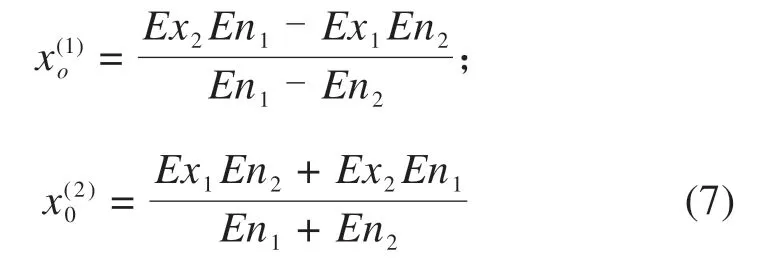
通过求解重叠面积S，可得到2组数据的相似程度指标。设Ex1≤Ex2，x(1)o≤x(2)o，分3种情况讨论不同工况云模型的重合面积，当2个交点均不在3En区间内时，2组云模型数据的重叠面积为0；当2个交点均在区间内时，面积计算公式如式(8)～(9)所示，即需根据云模型数据En大小情况进一步讨论重叠面积；当2个交点仅1点在3En区间内时，重合面积计算公式如式(10)所示。

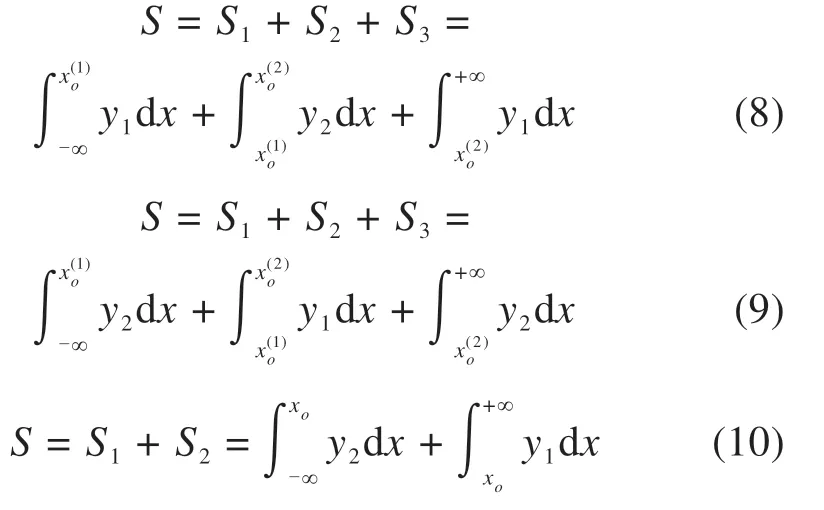
文献[16]中给出了计算云模型期望曲线相似程度的具体办法，以单个交点情况为例，期望曲线的表达式类似于正态分布的概率密度函数，可对期望曲线表达式做相应的处理。

根据正态分布相关理论，可对式(10)进行变形进而求解出重合面积S，求解过程如下所示。

对面积S进行标准化处理，最终可得到基于期望曲线的云模型相似程度(即损伤位置判别指标)。

2.2 基于云模型数字特征的损伤程度识别

识别出结构的损伤位置后，需要再进一步对单元的损伤程度进行定量分析。云模型的期望值Ex是云的重心位置，代表了该概念量化的最典型样本。为此，采用损伤单元云模型期望值变化来识别单元的损伤程度，即判定单元i发生损伤后，将该单元在不同工况下损伤系数云模型的期望值相减，得到ΔExi，通过其数值大小可反应该单元的损伤程度。

综上，所提方法的计算流程如图2所示。

图2 所提算法的计算流程图Fig.2 Calculation flow chart of proposed method

3 数值计算

以图3所示的二维23杆桁架结构为例，验证所提方法的可行性。材料参数为：杆单元长度L=1 m，横截面积A=1×10−4m2，密度ρ=7 300 kg/m3，弹性模量E=2.1×1011N/mm2。假设损伤前后各单元的质量不变，采用降低单元刚度模拟结构损伤，共设置3种损伤工况：1)单元E3损伤程度为5%；2)单元E3和E12的损伤程度分别为5%，20%；3)单元E3和E12的损伤程度分别为10%，20%。

图3 23杆平面二维桁架结构Fig.3 23-bar truss structure

采用基于不完备频响函数的损伤识别方法，计算出单元损伤前后的损伤系数ru和rd，为了考察噪声对识别的结果的影响，在频响函数数据中分别加入噪声水平为5%，10%，15%和20%的随机噪声，添加方式如下

式中：HA(ω)为由刚度矩阵和质量矩阵推导出的频响函数；a为加入的噪声水平；ξ为标准正态分布的随机数。

图4给出了不同噪声水平下工况1中E1和E3单元损伤系数的计算结果。从图4中可知，5%的噪声条件下，各单元损伤系数与设置损伤程度较为统一且数据离散程度较小。随着噪声水平的增加，损伤系数逐渐偏离真实值，离散程度增加。根据计算结果可知，基于不完备频响函数的损伤识别方法在实际应用中易受到噪声条件的影响造成识别结果误差。

图4 不同噪声水平下工况1损伤识别结果Fig.4 Damage identification results of case 1 under different noise levels

以噪声水平10%为例，将单元损伤前后的损伤系数作为初始输入，通过云模型发生器生成对应工况的云模型图。其中工况2部分单元的云模型图及对应的期望曲线如图5(a)～5(c)所示。由图可知，损伤前后健康单元E1的云模型期望曲线区别较小，重叠面积较大，单元相似度结果SECM为90.67%，而同种噪声水平条件下，损伤前后单元E3和E12的2组云模型的重合面积较小，即相似程度较低，且损伤程度越大，相似程度越小，如单元E12损伤20%的情况下，其相似度为0。由此可知，通过ECM法可有效区别损伤单元及健康单元，从而达到损伤定位的目的。

图5 工况2部分单元云模型图(考虑10%的测量噪声)Fig.5 Cloud models of some elements for Case 2(considering 10%noise)

3.1 噪声对损伤识别结果的影响

为验证ECM法的抗噪性，选取传统云模型相似性度量法中的夹角余弦法(LICM)进行比较，结果如图6所示。从图中可以看出，ECM法在4种噪声水平下可准确识别出3种损伤工况的损伤位置，如工况2，在噪声水平为5%时，损伤单元E12的SECM结果为0%，其余健康单元的SECM结果为96.17%～96.18%。随着噪声水平增加至20%时，E12单元的SECM值为5.31%，其余健康单元的SECM值下降至92.03%～92.04%。而LICM法随着噪声水平的增加，损伤单元与健康单元的相度区别逐渐减小，对结构进行损伤识别的难度逐渐加大。综上可知，相较与LICM法，ECM法的识别结果受噪声影响较小，具有更加优异的抗噪性，即使在20%噪声水平条件下，该方法亦能有效识别损伤单元的位置。

图6 不同噪声水平下3个损伤工况的S ECM，S LICM识别结果Fig.6 S ECMand S LICM of three damage case under different noise levels

不同噪声条件下损伤单元损伤程度识别结果及误差如表1所示。从表中可知，E3和E12单元在3种工况下的损伤程度与理论值较为吻合，如5%噪声水平时，工况1中E3单元损伤程度为4.98%，误差为0.40%，随着噪声水平的增加，损伤程度识别误差逐步增大，但仍然在工程精度要求范围内。

表1 不同噪声水平下E3和E12单元损伤程度计算结果及误差Table 1 Identification results and errors of damage degree of E3 and E12 elements under different noise levels

3.2 重复测量次数对损伤识别结果的影响

在实际工程应用时，尤其针对大型结构，多次测量频响函数数据往往需要耗费大量人力和物力资源。为了探讨所提方法在小样本情况下的适用性，分别取重复测量次数为10，30，50，100。在10%的噪声水平下，不同重复测量次数下3种工况的识别结果如图7所示，从图中可知，当重复测量次数为10时，ECM法仍可以准确识别损伤单元的位置，不同重复测量次数对ECM法的损伤定位结果的影响较小，即使在小样本(原始样本个数为10)情况下，ECM法仍可有效区别损伤单元与健康单元，具备一定工程应用价值，而LICM法则易受到原始样本数目影响，当样本数据较少时，通过LICM法无法准确区别损伤单元与健康单元。

图7 不同重复次数下3个损伤工况的S ECM，S LICM识别结果Fig.7 S ECM and S LICMof three damage case under different repeated measurement times

不同重复测量次数下单元损伤程度识别结果及误差如表2所示，当重复测量次数为10时，E3单元在工况1的损伤程度为5.69%，随着重复测量次数增加至100，损伤程度变化为5.19%，与设置程度5%的误差逐渐减小，从表中可知，损伤程度最大识

表2 不同重复测量次数下E3和E12单元损伤程度计算结果及误差Table 2 Identification results and errors of damage degree of E3 and E12 elements under different repeated measurement times

别误差不超过16%，具有良好的识别精度与工程应用价值。

3.3 无健康工况数据条件下损伤识别结果

损伤识别方法在实际工程应用中常面临无法取得结构在健康工况数据的问题。为了验证所提方法在无健康工况数据条件下能否对结构进行损伤识别，选取10%噪声条件下的工况2进行研究。识别结果如图8所示，损伤单元E3和E12与其余健康单元的SECM数值范围分别为28.29%～34.09%和0%，其余健康单元的SECM数值范围为93.63%～100%，所提算法可有效识别损伤单元，达到损伤定量的目的。