磁通等效容错控制下两磁极故障分析
2022-06-08朱芳甫陈亮亮王恒蒋科坚
朱芳甫,陈亮亮,王恒,蒋科坚
(1.浙江理工大学 信息学院,杭州 310018;2.南昌航空大学 信息工程学院,南昌 330063)
0 引言
磁悬浮轴承系统在运行过程中无机械接触产生的摩擦力,避免了摩擦能量损耗和发热,广泛应用于工业生产、交通运输、医疗器械、风洞模型和机械隔振[1]等领域。执行器是主动磁悬浮轴承系统的重要组成部分,其将控制器输出的电压控制信号转换为相应的控制电流信号,输入到电磁线圈产生电磁力,使转子能够稳定悬浮在设定的位置;然而在高温高压等环境中,执行器的故障概率很高,一旦发生故障将导致高速转子悬浮失控从而引发事故。
国内外学者针对磁悬浮轴承系统的执行器故障进行了理论分析及试验研究:文献[2]提出了一种新型电磁作动器故障诊断算法,将负载电流的等效斜率作为阈值诊断故障;文献[3]提出具有冗余结构的异极磁悬浮轴承精确线性化方法,求解电流分布矩阵的泰勒级数展开方程并建立了包括受控电流和转子位置的精确模型;文献[4]介绍了九磁极混合磁悬浮轴承的结构和容错机理,推导了悬浮力的数学模型,分析了2种悬浮力补偿方法并进行了验证;文献[5]针对紧耦合冗余支承结构主动磁悬浮轴承提出了一种容错控制策略,在电磁作动器发生故障的情况下通过补偿磁通损耗对其余结构进行重新配置并提供预期的支承力;文献[6]提出了一种基于PI增益自动调谐的容错控制方法,降低了计算复杂度并证明了其在处理建模不确定性和非线性以及驱动故障方面的有效性;文献[7]利用轴承-转子系统结构模型对执行器故障进行了可检测性和隔离性分析;文献[8]研究了一种新型三相表面永磁电动机的容错控制技术,利用电流控制技术避免在一个机器扇形绕组开路的情况下出现径向力,并通过有限元仿真验证了控制方法的有效性;文献[9]提出一种针对磁悬浮轴承的在线电磁线圈故障诊断方法并通过仿真验证了该方法的可行性;文献[10]基于有限元法建立电磁模型,通过仿真计算电动机的起动性能并证明了模型的准确性;文献[11]提出了2种半受控条件下开环绕组五相电动机驱动的容错重构策略,仿真和试验结果均验证了2种重构策略的可行性;文献[12]提出以“电磁力等效”为控制目标的分配策略,求解了电流分配矩阵并同时验证了该方法在一个或多个磁极故障情况下的可行性;文献[13]提出 “磁通等效”方法,通过对8个磁极驱动电流的重新分配实现容错前后的转子悬浮磁通环境一致,从而实现电磁力一致,并验证了一个磁极故障时磁通等效的可行性。
上述文献对电磁轴承容错控制的研究大致分为2类:1)对电磁轴承结构上的容错,一般是改变磁极拓朴结构进行容错控制,但会使电磁轴承系统更为复杂;2)对电磁力的容错,一般采用“电磁力等效”进行电磁轴承容错控制,即当磁极绕组控制回路发生故障时,由正常的磁极承担故障磁极的电磁力任务并产生与未发生故障前相同的电磁合力,从而达到电磁轴承容错控制的目的;但由于电磁力与电流成非线性关系,难以得到准确换算关系,因此难以对故障后的等效电磁力进行精确控制。
本文采用文献[13]提出的“磁通等效”方法进行容错控制,并分析电磁轴承在2个磁极故障情况下故障磁极极性和相对位置变化对容错实现的影响。
1 电磁轴承的电磁力
八磁极电磁轴承的C型定子拓扑结构(图1)是最为常见的径向电磁轴承定子拓扑结构,一般采用差动控制方式。C型磁极的电磁力简化模型如图2所示。
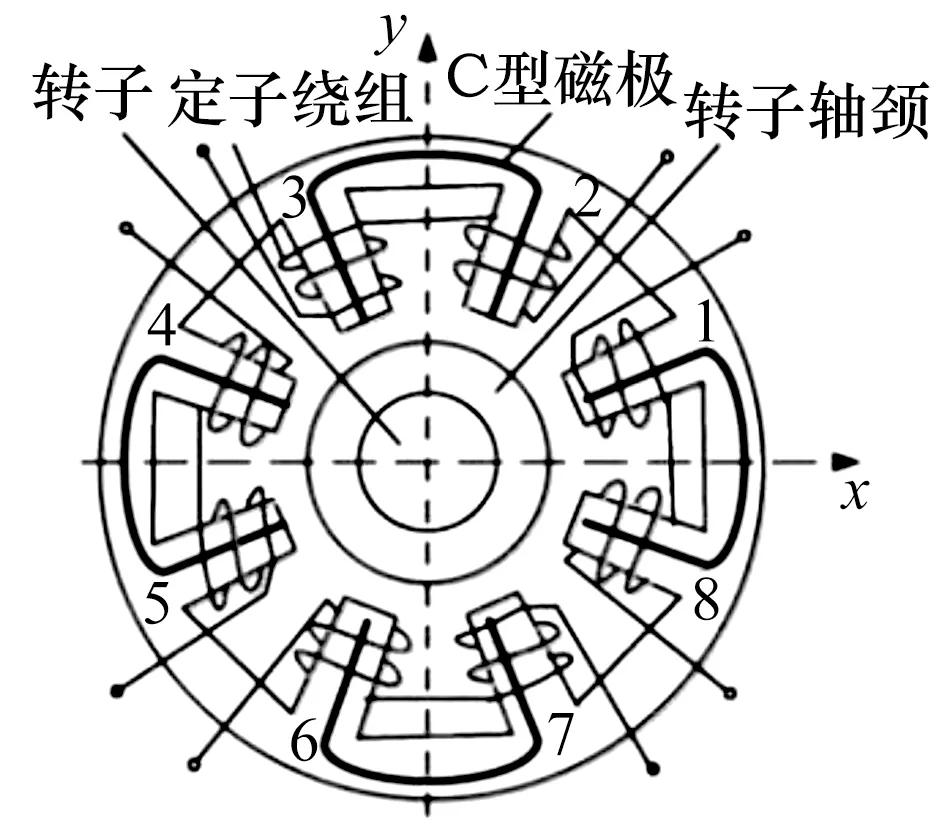
图1 八磁极电磁轴承C型定子拓扑结构Fig.1 Topological structure of C-type stator ofeight-pole electromagnetic bearing
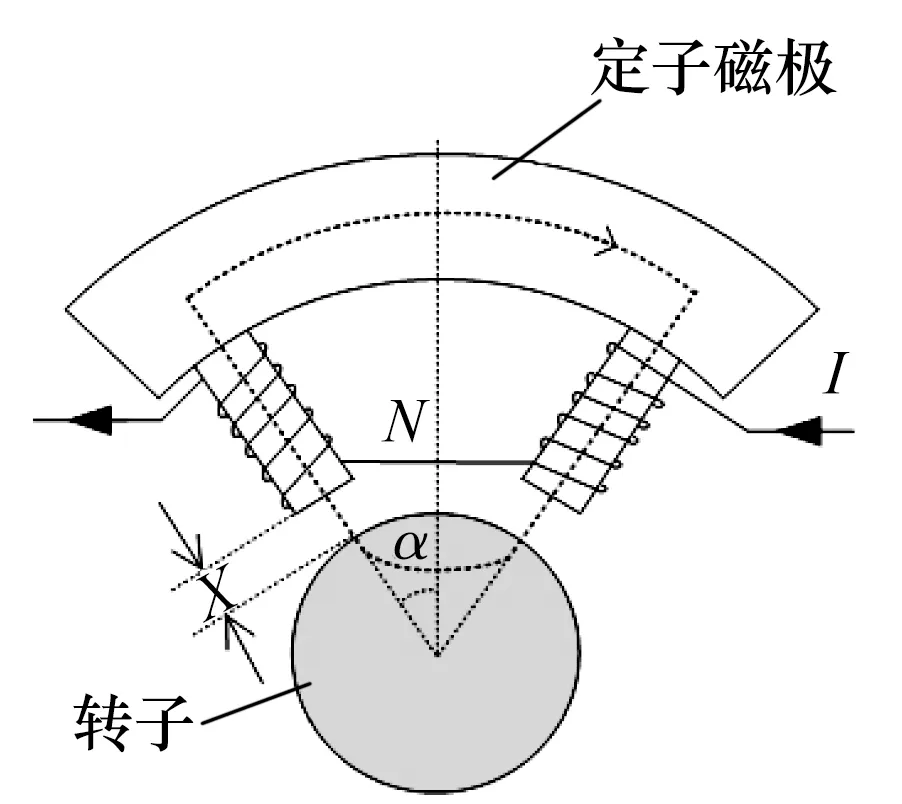
图2 C型磁极的电磁力简化模型Fig.2 Simplified electromagnetic force model ofC-type pole
依据麦克斯韦方程组,推导出单个C型磁极对转子的电磁力为
(1)
式中:μ0为真空磁导率;A为定子与转子间气隙的横截面积;N为磁极线圈匝数;I为线圈控制电流;c为定子与转子间的气隙宽度;α为两磁极夹角的一半。
4个C型磁极可以产生坐标轴方向的正负4个电磁力,使转子悬浮。由于4个电磁力在方向上没有冗余,当其中1个方向电磁力失常时,其余3个方向的电磁力无法为故障磁极提供所需电磁力,无法进行容错控制。
为实现多个磁极绕组故障的容错控制,将每个C型磁极拆分为2个独立的定子磁极,得到如图3所示的径向八磁极独立电流的定转子拓扑结构,其中a1,a2,…,a8分别表示定子磁极上的绕组。每个定子磁极上的绕组都是独立的,形成8路独立的绕组控制回路,此结构下,8个电磁力在方向上有冗余,磁极绕组回路通电后在每个磁极内产生耦合磁通,并且当转子处于稳定悬浮状态时磁极内的磁通动态不变,从而实现系统的容错控制。

图3 径向八磁极独立电流的定转子拓扑结构Fig.3 Topological structure of stator and rotor withradial eight-pole independent current
2 磁通等效的电流重构
磁通等效方法需要耦合能力较强的结构,强弱耦合的主要区别在于磁极与磁极间的耦合关系。图4a为弱耦合结构(NNSS型),磁极仅与相邻一侧的异极性磁极构成磁力线回路,分别形成4个磁力线回路且回路之间耦合能力较弱。图4b为强耦合结构(NSNS型),某一磁极与相邻2个磁极的极性均为异极性,形成8个磁力线回路且耦合能力强于NNSS型,更利于磁通等效的控制方式。
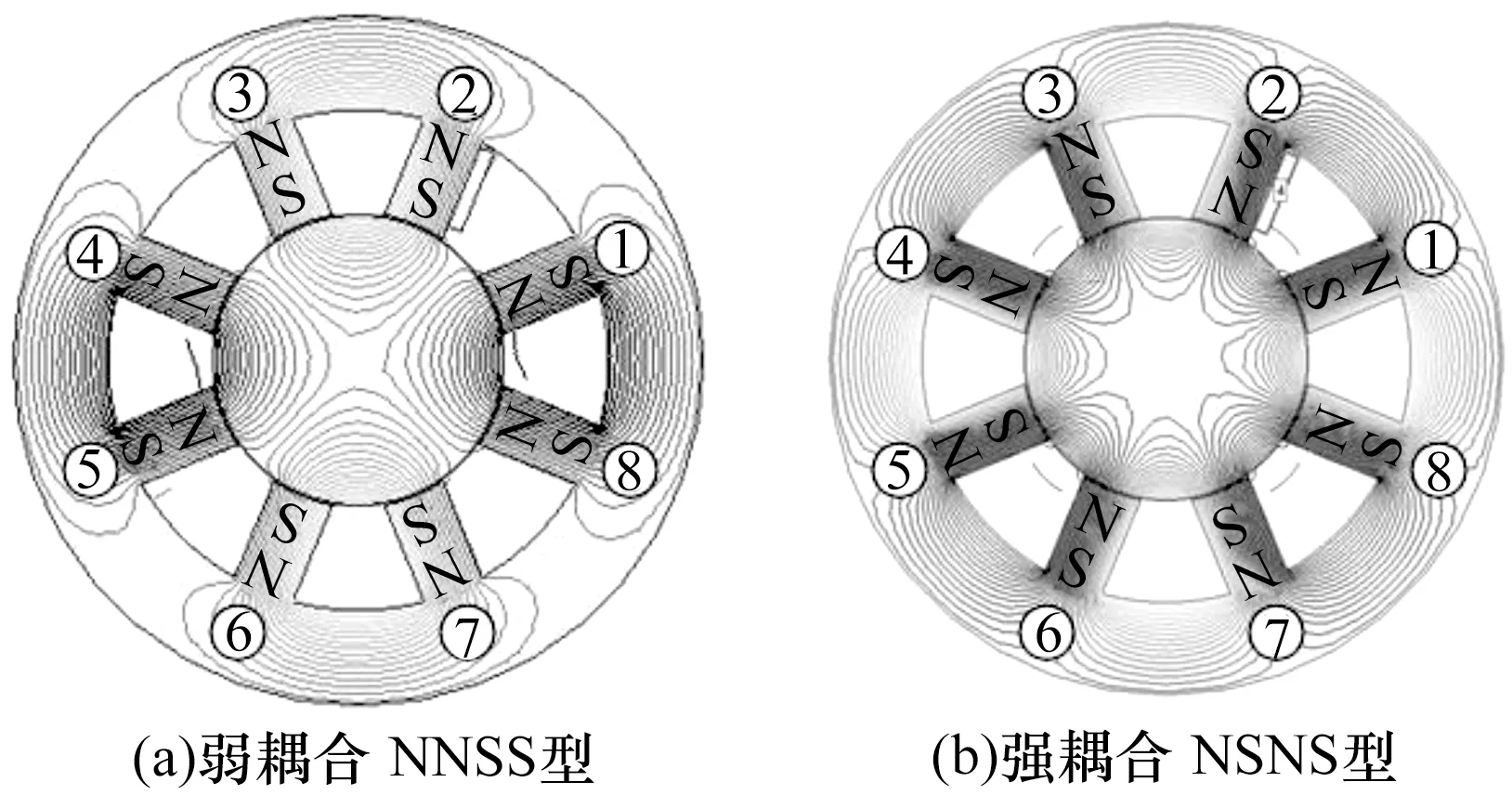
图4 强弱耦合拓扑结构图Fig.4 Topological structure diagram of strongand weak coupling
本文提出电流-磁通影响系数法,假设定子磁极绕组通电时各个磁极的有效磁通ψ=[φ1φ2φ3φ4φ5φ6φ7φ8]T,各个定子磁极绕组的工作电流I=[i1i2i3i4i5i6
i7i8]T,则有
MI=ψ,
(2)
式中:M为磁极正常时的磁通影响系数矩阵。
假设八磁极独立电流电磁轴承的一个定子磁极绕组回路发生故障, 以1#磁极绕组回路发生故障为例,由(2)式得
MI1=ψ,
(3)
I1=[0 0i3i4i5i6i7i8]T,
式中:I1为1#定子磁极绕组回路故障时各个绕组回路的控制电流。
(3)式可理解为用6个磁极产生最接近期望值的8个磁极的端面磁通的超静定方程。将(3)式化为重构电流矩阵形式
KI2=ψ,
(4)
式中:I2为磁极绕组故障后磁通不变的重构电流;K为M矩阵删去第1列后得到的子矩阵,表示除故障磁极绕组外其他正常磁极的磁通影响系数矩阵。
根据超静定方程最小二乘定理,(4)式可转化为
KTKI2=KTψ,
(5)
将(3)式代入(5)式化简可得
I2=(KTK)-1KTMI1。
(6)
(6)式表示定子磁极绕组故障前、后的电流关系,从而可以求得故障后保持有效磁通不变的绕组回路控制电流,令W表示故障前、后的电流分配矩阵,则
W=(KTK)-1KTM。
(7)
3 2个磁极回路故障的磁通等效容错控制
在2个磁极回路故障情况下,利用ANSYS仿真软件对磁通等效容错控制方法求得的电流分配矩阵进行验证。2个磁极回路故障可分为故障磁极同极性和异极性2类情况。
3.1 2个故障磁极为同极性
存在2个同极性故障磁极时,八磁极电磁轴承的磁感应强度和磁力线分布分别如图5、图6所示,其中左图为故障状态,右图为重构电流容错处理后的状态(下同)。
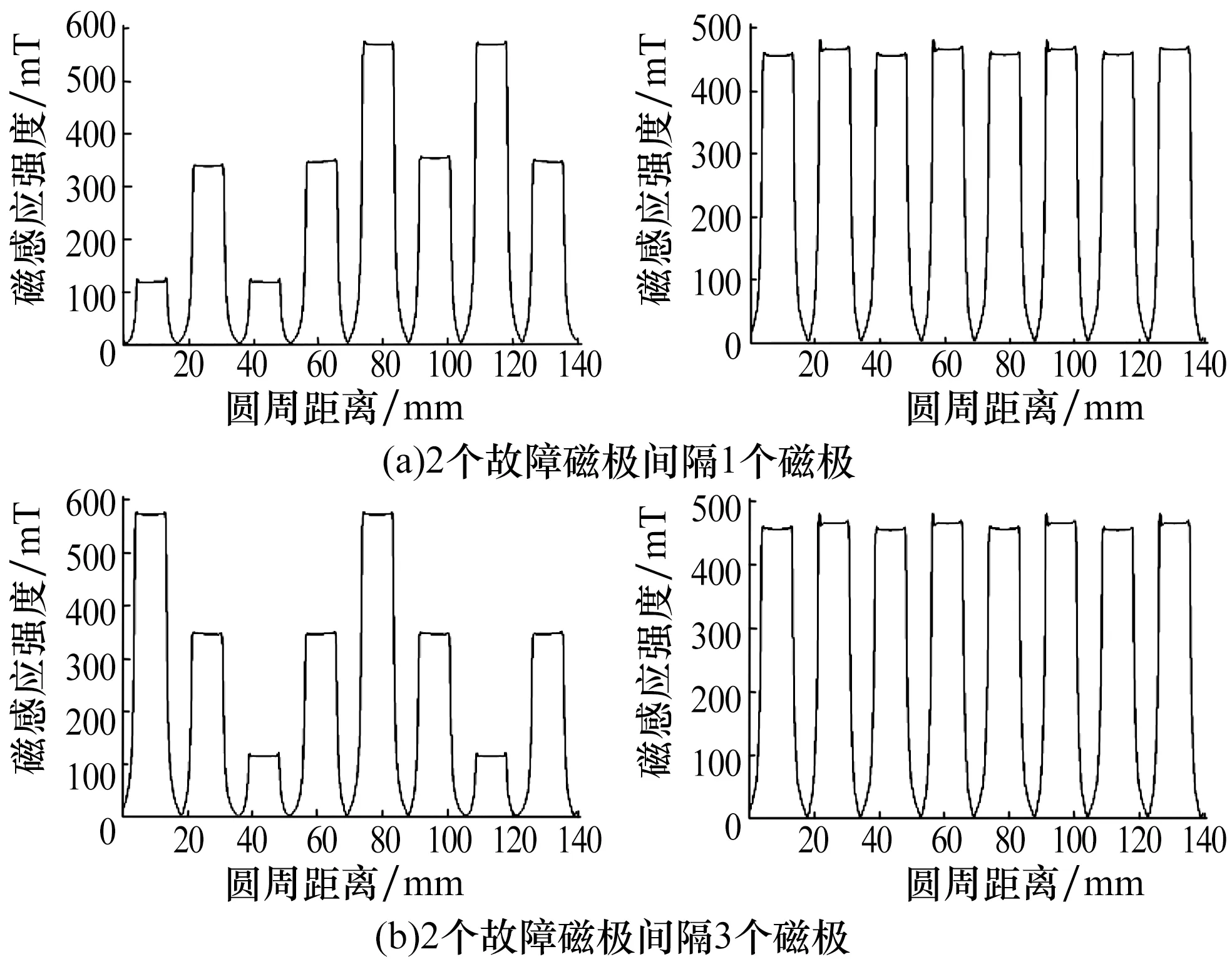
图5 2个故障磁极同极性时电磁轴承的磁感应强度Fig.5 Magnetic induction intensity of electromagneticbearing when two faulty poles are homopolar

图6 2个故障磁极同极性时电磁轴承的磁力线Fig.6 Magnetic line of force of electromagnetic bearingwhen two faulty poles are homopolar
存在2个同极性故障磁极的情况下,由于磁极间的耦合现象,磁感应强度和磁力线分布均发生变化;通过磁通等效容错控制后故障磁极相邻两侧极性相同相互排斥,不会直接在定子外圈形成回路,所形成的回路会经过故障磁极,经磁通等效后可以较好地恢复磁极端面的磁感应强度和磁力线分布,实现容错控制。
3.2 2个故障磁极为异极性
存在2个异极性故障磁极时,八磁极电磁轴承的磁感应强度和磁力线分布分别如图7、图8所示。
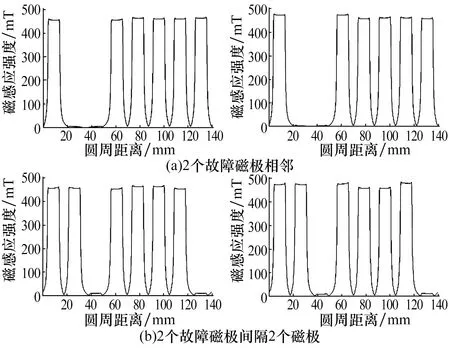
图7 2个故障磁极异极性时电磁轴承的磁感应强度Fig.7 Magnetic induction intensity of electromagneticbearing when two faulty poles are heteropolar

图8 2个故障磁极异极性时电磁轴承的磁力线Fig.8 Magnetic line of force of electromagnetic bearingwhen two faulty poles are heteropolar
存在2个异极性故障磁极的情况下,由于故障磁极绕组为异极性,故障磁极相邻两侧磁极极性不同会相互吸引形成回路,导致磁路改变不再经过故障磁极,经磁通等效后无法恢复磁极端面的磁感应强度和磁力线分布,无法实现容错控制。
4 结论
在磁通等效容错控制方法基础上,分析了电磁轴承存在2个磁极故障的情况下,磁极极性和相对位置变化对容错实现的影响:
1)2个故障磁极为同极性时,其余磁极能在故障磁极处形成磁通回路,磁通等效方法可以较好地还原故障前的端面磁通值、磁力线分布以及磁感应强度,实现容错控制。
2)2个故障磁极为异极性时,其余磁极不能在故障磁极处形成磁通回路,磁通等效方法无法还原故障前的端面磁通、磁力线分布以及磁感应强度,无法实现容错控制。
