基于迭代动态规划的动力电池组热管理优化策略*

马 彦，李佳怡，马 乾，陈明超

（1. 吉林大学通信工程学院，长春 130022；2. 吉林大学，汽车仿真与控制国家重点实验室，长春 130022；3. 吉林化工学院信息与控制工程学院，吉林 132000）

前言

能源的极度短缺和严重的环境污染已经成为全球性问题，为了减少温室气体排放，摆脱对石油能源的依赖，电动汽车被视为传统内燃机汽车可行的替代方案。锂离子电池放电率较低，功率密度高，可回收利用率高，电池循环寿命长，已被广泛应用到电动汽车。电动汽车运行中，动力电池组会持续放电，电流幅值会迅速上升，特别是在加速、爬坡等特殊工况下。当电池组处于放电过程时，其内部的化学物质相互作用，产生大量的热，过高的温度使电池的容量下降，寿命衰减，严重时会导致电池组燃烧爆炸。调节电池温度会消耗大量的电能，尤其是用于冷却电池。German 等基于电池模型与牵引模型，分析了温度对电动汽车行驶里程的影响。此外，电池热管理系统消耗的能量会减少电动汽车的行驶里程。当驾驶员开启空调系统等设备时，会大大消耗电池的能量，减少电动汽车40%的行驶里程。所以，在快速冷却电池温度的同时，减少冷却系统能量的损耗，对于延长电动汽车行驶里程，保证电动汽车运行安全性，提高整车性能至关重要。因此，采取高效的冷却优化策略对电池热管理系统十分重要。

锂离子电池热模型是研究电池组热管理的基础，由于电池冷却处于单次放电过程，电池老化和容量退化过程可以忽略不计，并认为电池的温度是均匀的，同时忽略了电池表面温度和核芯温度之间的差异。综上，集中质量热模型把电池当作一个质点，推导得到电池整体的平均温度，而非针对电池的单体温度，模型的建立和计算简单，适用于对锂离子电池整体性能和电池组的研究。Li等采用集中质量热模型预测电池模块的最高温度，但没有建立单体电池的热模型。Choi 等建立了18650 型锂离子电池的降阶集中质量热模型，但未考虑电池的散热情况，没有推导传热系数与冷却液流速之间的关系。针对上述问题，本文在分析液体冷却的电池组的流体动力学规律的基础上，建立液冷式电池组集中质量热模型为后续的热管理优化策略提供理论基础。

目前电池热管理系统冷却方式有空气冷却、液体冷却、相变材料冷却和热管冷却。文献［16］和文献［17］中对比了风冷和液冷两种独立的热管理方案，液冷在冷却速度、密封特性和对环境温度影响的抵抗能力等都要远优于风冷，且电池电量的消耗也小于风冷的形式。液体冷却在结构上又可分为接触式液冷和非接触式液冷，前者采用导热率高且绝缘的液体作为冷却液，在物理性质上具有较高的黏度，导致水泵需要增加额外的功耗。非接触式液冷中，冷却液在冷却管道中流动，通过物理装置与电池间接接触，换热效率高，冷却速度快，且冷却液流速稳定，在电池大电流充放电和夏天等高温极端条件下有很好的冷却效果。因此，本文的冷却方式为非接触式液体冷却。

冷却优化策略的研究主要是实现系统以最小的能量损耗对电池运行温度的调节，避免电池温度过高和降温同时系统的高能耗。控制类方法可以实现有效的温度调节效果，便于应用于实际，而优化类方法旨在使电池在加热或冷却过程中处于合理的温度范围，即最优优化策略是寻求温控和节能的一个平衡点。因此，选择优化类算法目的是在保证动力电池在适宜温度范围内运行的基础上，进一步降低冷却系统的能量损耗。文献［19］和文献［20］中采用模糊控制的方法虽然不需要依赖被控对象准确的数学模型，在冷却效果上优于传统PID 的方法，但节能效果有限。Masoudi 等提出非线性模型预测方法有效性的调节电池温度，但是没有考虑热管理系统的冷却能耗。Bauer 等利用庞德里亚金极大值原理实现了电动汽车中利用最小的电能损耗使电池在较窄的温度范围内运行。Tao 等针对风冷系统提出非线性反步控制器和线性最优控制器控制进风温度，从而稳定电池核心温度，与传统控制器比较节省能耗方面得到改善。Pham 等针对混动重卡汽车突出基于规则的实时策略，提高燃油经济性的同时降低了电池的能量消耗。Yuksel等提出启发式策略和基于约束的非线性规划策略用于燃料电池混动汽车的能量管理系统，实现降低氢能耗的17%。Lopez等在非线性模型预测控制方法的基础上，在约束上进一步考虑了电池冷却能量的消耗，实现了冷却过程中冷却能量的最小化，但是没有考虑液冷系统参数不确定性的影响。Zhu 等提出一种基于有限集模型的混合动力汽车电池热管理系统鲁棒预测优化策略，在50%的参数不确定性下，不仅可以使电池组在最佳温度下运行，而且节省30%的电池热管理系统能量。文献［28］和文献［29］中提出基于MPC 的精确冷却策略和生态冷却策略，实现对电动汽车的高效热管理，进一步降低4.9%和8%的空调系统能耗。

综上所述，由于被控对象电池冷却系统的高度非线性、参数时变和迟滞的特点，为了保证电池的工作环境、能够快速降低运行温度，同时实现节能的目的，需要选取能寻求非线性连续系统全局最优解的算法。动态规划方法（DP）被提出用来调节电池组的温度，实现冷却能量的最小化。但是由于DP优化策略较为复杂，在计算时间还是在计算量上都是巨大的，在实际中考虑成本的约束，始终难以实时应用。为了克服DP 算法的缺点，文献［31］～文献［34］中提出迭代动态规划（IDP）算法，避免求解高维非线性连续系统的H-J-B 方程，减少计算量，易于实现，适用于非线性连续系统动态规划。基于以上研究，本文采用IDP 算法作为冷却优化策略应用到电池热管理系统，以最小的能量损耗使电池组温度稳定在目标温度范围内。

本文结构如下：（1）根据电池的生热特性和牛顿冷却定律建立电池组集中质量热模型，在AMEsim中建立电池冷却系统，在不同工况下验证模型的准确性；（2）针对冷却系统的非线性与时变性的特点，提出基于IDP 算法的冷却优化策略；（3）基于IDP 优化策略与PID 方法和DP 优化策略进行仿真比较，验证所提出的方法在冷却过程中的快速性与节能性的优势；（4）给出IDP冷却优化策略的相关结论。

1 电池组模型建立及可靠性验证

在本部分，分析电池内部的生热原理和电池散热过程中的动力学和传热学原理，建立生热量和散热量方程。利用能量守恒定律确定电池组与冷却液之间的能量传递关系，建立基于液冷式电池组集中质量热模型。

1.1 锂离子电池生热模型

电池液冷系统示意图如图1 所示，锂离子电池在工作过程中，电池的总生热包含4 个部分，分别是电池内阻热、电池反应热、电池极化热、电池副反应热，可描述为

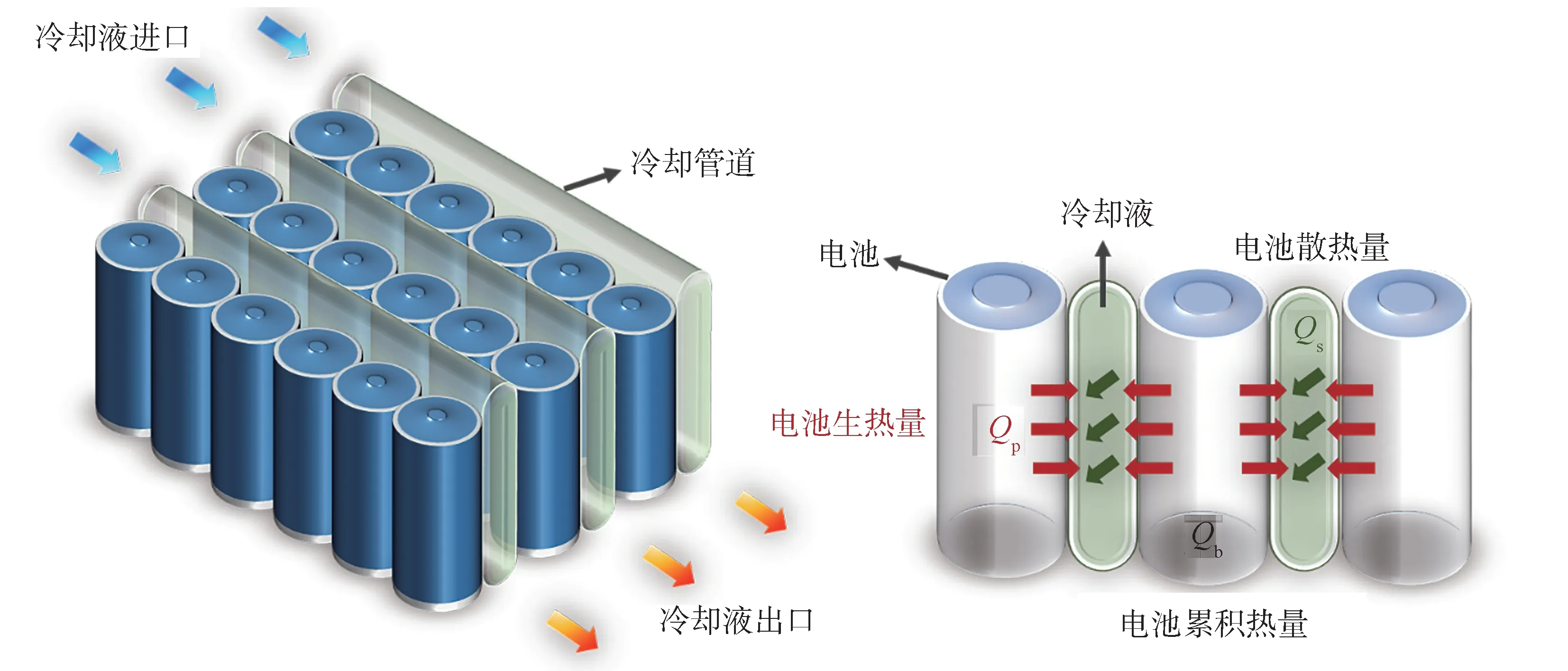
图1 电池液冷系统示意图

对于电池生热部分，根据动力电池Bernadi 生热速率模型，假设锂离子电池内部热源稳定且均匀产热，从电池内阻和化学反应的熵增原理两个方面考虑，把电池的极化热和反应热均考虑为可逆反应热，可得到电池的生热率，即

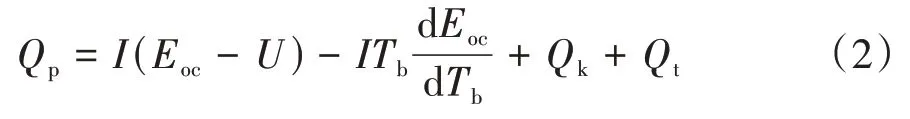
式中：是开路电压；是工作电压；是电池的温度；是电池的工况电流。由于电池内阻的存在，(-)表示的开路电压与工作电压之差可用电流与内阻的乘积来进行等量代替，则式（2）可以表示为

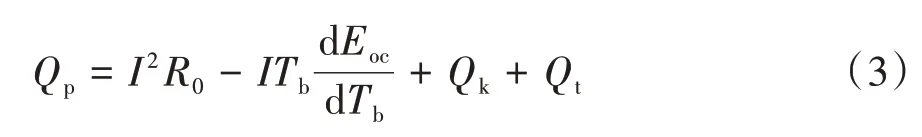
右侧第1部分代表电池内阻热，第2部分代表电池内部反应热，第3 部分代表电池极化热，第4 部分代表电池副反应热。电池进行正常充放电情况下，如果沿电池厚度方向的电池温差很小或电池很薄，就可以忽略电池的极化反应热和副反应热。假设电池内部电流密度一致且生热均匀，锂离子电池生热率可简化为

其中，对于电池的内阻，对其影响最大的两个参数是电池的放电深度和温度。当锂离子电池工作在293～313 K、放电率在10%以上时，电池内阻变化不大。因此可认为电池包内阻为常数，设为=0.8 mΩ。而d/d与电池的电化学反应相关，对于同种类的电池，该值可认为是常量，设为=0.3 mV，通过两个参数的确定可以得到单体电池的生热速率与负载电流的函数关系为

1.2 锂离子电池散热模型

根据牛顿冷却定律，可以得到电池与冷却液间对流传热散失总热量为

式中：为电池散热量；为流体与固体接触表面间的对流传热系数；为对流换热面积；为冷却液温度。电池与冷却液之间的对流传热系数与管内流体努塞尔数的关系为

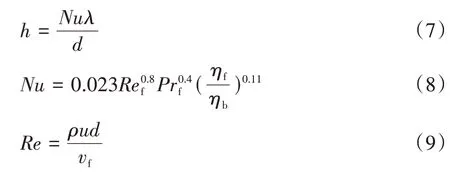
式中：为流体的导热系数；为流体管道的当量直径；为管内流体雷诺数；为管内流体普朗特数；和分别是按流体平均温度和管壁温度计算的流体动力黏度；为管内流体的平均速度；为管内流体的运动黏度。冷却液的热物性参数、、均可由管内流体平均温度查表得到，可由管壁附近流体温度查表得到。由式（7）～式（9）可得电池与冷却液间的对流传热系数与冷却液流速之间的关系为

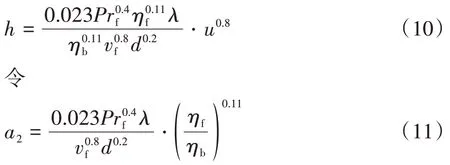
将式（10）和式（11）代入到式（6）中，得到的电池散热模型中电池散失的总热量为

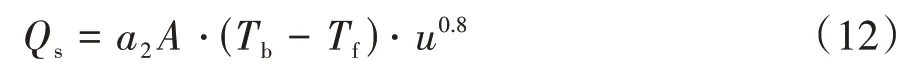
1.3 锂离子电池组热模型

由能量守恒定律可知，对于处于充放电状态下的电池，电池积累的热量等于电池内部电化学反应的总生热量减去电池与冷却液热交换的总散热量，即

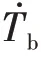
式中：为电池质量；为电池的比热容。则电池热模型为

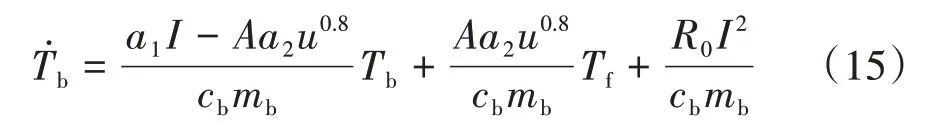
在每行排列中，1 号电池模组处于冷却管道入口处，末端电池模组处于冷却管道出口，冷却液从入口到出口会不断吸收热量导致冷却液温度升高，故1 号模组温度要低于末端电池模组。因此，建立首尾两个电池模组的热模型，即可得整个电池组温度分布情况。由式（15）可得1 号电池模组热模型，表示为

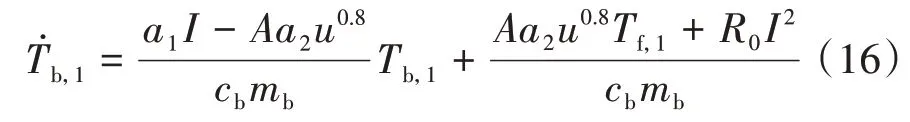
电池组中每行模组总散热量等于此行管道内冷却液从入口到出口的总吸热量，根据能量守恒定律可知：

由传热学定律，单位时间内电池组冷却管道内冷却流体从入口到出口散失的热量总和为

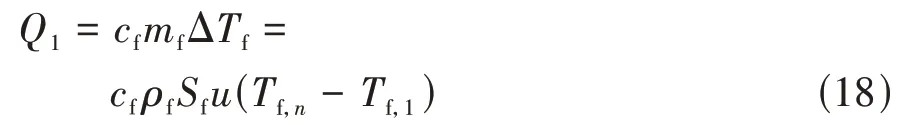
式中：为冷却液比热容；为冷却液密度；为入口处冷却液面积。冷却流入吸收的热量总和为

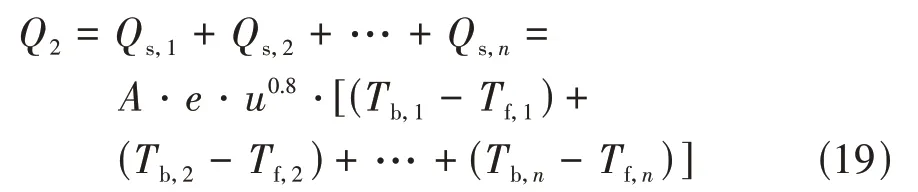
式中：、、…、分别为1号电池模组到号电池模组散失到冷却液的热量；、、…、分别为1 号 电 池 模 组 到号 电 池 模 组 的 温 度，，、…、分别为1 号电池模组到号电池模组周围冷却液的温度。在电池组冷却管道内沿冷却液流动方向，可认为每个电池周围的冷却液温度呈等幅递增的状态，故可得

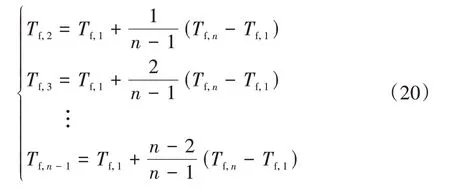
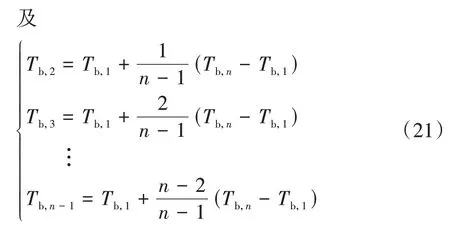
由式（20）和式（21）可得号电池模组周围冷却液温度为

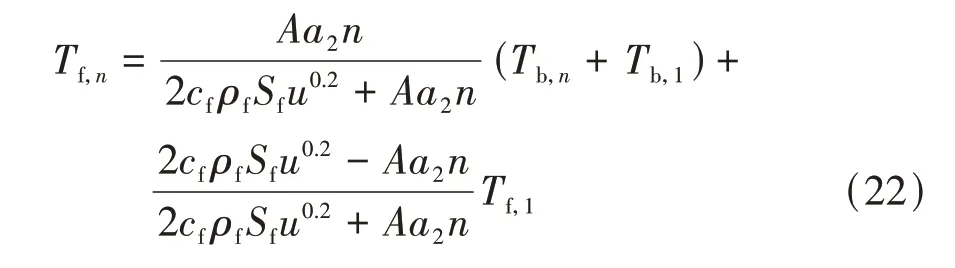
将式（16）和式（22）代入式（15）得号电池模组的热模型为

由上述公式可以看出电池组热模型是关于液体流速的非线性函数，系统输入量为负载电流，控制量为冷却液流速，系统输出量是电池温度、，故电池组热模型可简化为

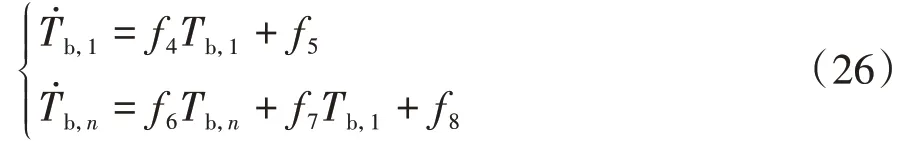
1.4 电池组模型可靠性验证

为验证模型精度，在AMESim（advanced modeling environment for performing simulation of engineering systems）中建立电池组模型，将AMESim 中得到的电池温度变化数据作为实际测量值，来验证所建立模型的精度。

电动汽车动力电池组是由固定数量的电池模组根据续航里程、电池容量等设计要求串并联而成，而电池模组是由一定数量的电池连接而成，模组的外壳保持电池的位置和形状。本文中电池模组由18*18 A123 26650 LiFePO电池组成，采用7 个模组串联，对电池模组中的电池热行为进行分析，单节电池电压为3.3 V，容量为2 300 mA·h，冷却液选择50%体积浓度的乙二醇水溶液，电池与冷却液初始温度设置为298 K，AMESim 电池组冷却系统模型如图2所示，其具体物理参数如表1所示。

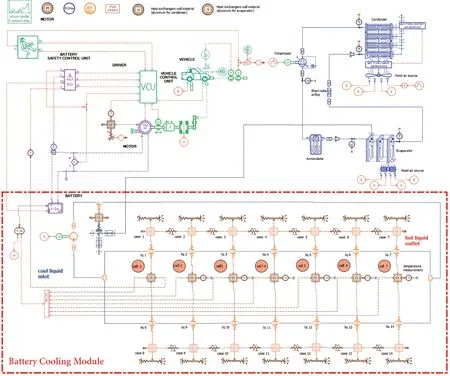
图2 AMESim电池组冷却系统模型

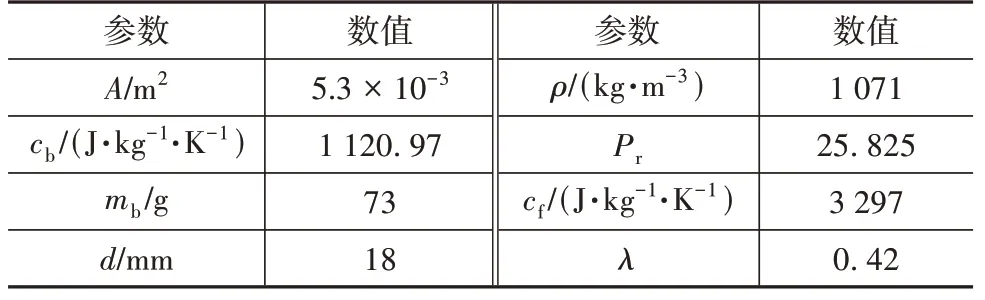
表1 AMESim 模型与冷却液物理参数

在模型验证过程中，NEDC 工况包含4个城市循环和一个市郊循环，US06 是高速和高加速度工况，所以两个工况能基本满足全路况状态，NEDC、US06工况车速与电流如图3 所示。分别在NEDC、US06工况下对比热集中模型与AMEsim 模型中模组的输出温度。电池模组输出温度与误差曲线如图4 和图5所示。

图3 NEDC和US06工况下车速与电流

通过图4 和图5 可以看出，在两个工况下，电池温度随负载电流变化逐渐上升。电池组热模型的输出曲线能很好地跟踪实际输出值，并且保证温度误差在0.7 K 以内，能够满足精度要求，故电池组热模型可用于后文冷却优化策略设计。

他们出身各异，经历不同，但“英雄不问出处”，能在全球化的浪潮中脱颖而出，在市场经济竞争里撑起场面，绝非等闲之辈。

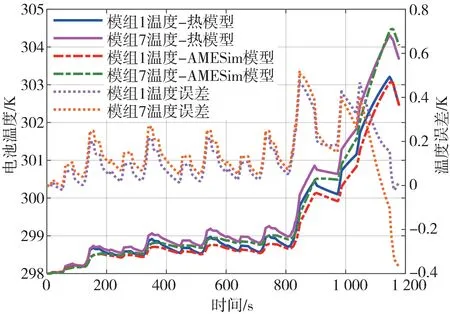
图4 NEDC工况电池模组温度与误差验证

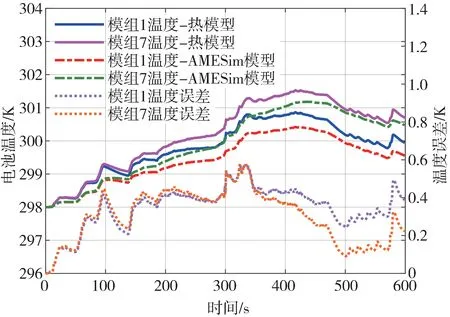
图5 US06工况电池模组温度与误差验证

2 迭代动态规划（IDP）优化策略

针对电池组热模型高度非线性和时变的特点，动态规划算法（DP）总能找到离散控制问题的全局最优解，但是由于必须比较每个控制与状态之间的网格点以获得最小的代价，需要大量的处理器内存来存储各个网格点所计算的目标函数和代价函数，导致计算时间过长。因此，提出迭代动态规划（IDP）算法，它是一种数值方法，鲁棒性强，通过多次应用基本的动态规划来减少子问题的数量和计算时间。该算法通过网格精细化的处理方式，进行逐级缩小范围搜索，最终获得动态优化问题的最优控制策略及最优轨迹。可以避免动态规划算法耗时及存在“维数灾”等诸多问题。

根据式（24）～式（26），电池组温度控制系统的状态空间方程可表示为

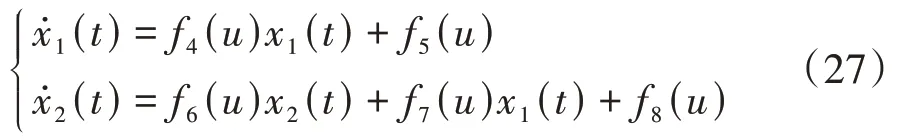
式中：=[，]。分别把第1个模组温度和第号模组温度作为状态量；控制量为冷却液流速；和作为系统输出。式（27）的电池组离散后热模型为

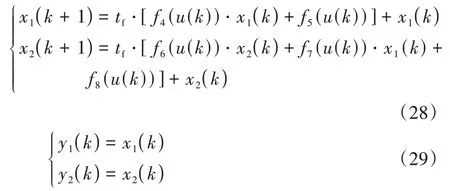
通过控制冷却液流速以最节能的功率方式优化电池组温度，建立液冷热管理系统的目标函数：

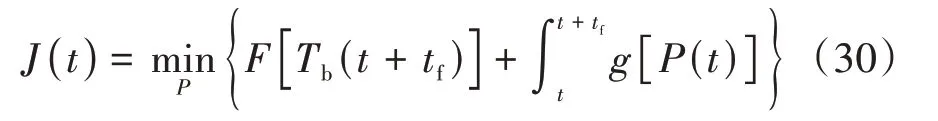
式中：[(+)]为电池组温度变化的代价函数；[()]为冷却系统的能量消耗。根据时段内可能发生的电池组的温度变化和冷却系统的能量消耗，建立液冷热管理系统约束函数，()为电池温度，()为冷却系统的能量消耗，为能量消耗阈值，和为电池组可工作的最高温度和最低温度，即

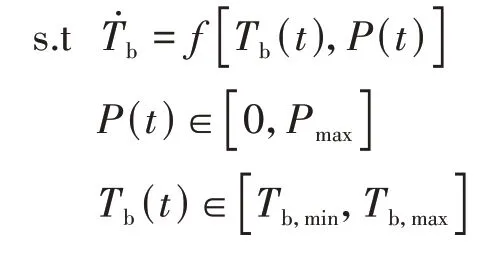
建立液冷系统的温度代价函数

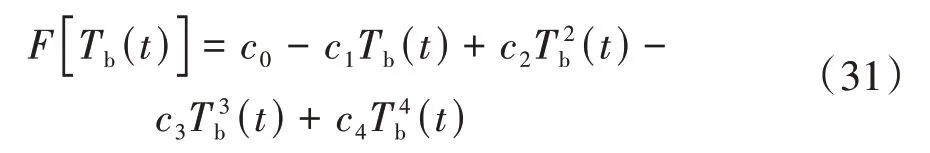
式中，= 0.2636，= 1.285 × 10，= 2.47 × 10，= 1.847 × 10，= 5.316 × 10，是通过曲线拟合获得的老化系数。定义为能耗比例系数，液体冷却系统消耗的能量与质量流量关系可定义为

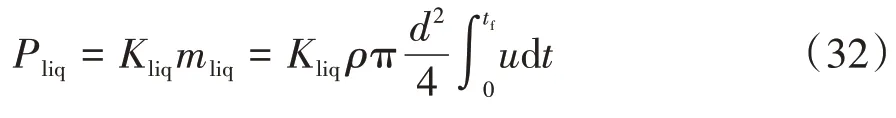
在初始的迭代中实现基本的DP算法，以找到网格中每个状态点x的最佳控制矢量，即使用粗略控制和状态网格搜索初始最佳轨迹。然后，在下一次迭代中通过将代入到电池液冷热管理系统的状态转移矩阵中来确定初始最优状态轨迹和相关的控制轨迹。选择获得的状态和控制轨迹作为下一次迭代的网格中心点。当状态网格点数固定，网格大小Δ由状态变量的约束范围确定。取衰减因子为，使网格大小Δ减小，即随着每次迭代中的间隔缩小，网格尺寸逐步减小，导致最优轨迹的搜索范围缩小，如图6 所示。图7 为IDP 算法的边界收敛图，在迭代时间N中逐步减少状态数量和控制量直到获得最小损耗下的最佳轨迹，IDP 优化策略流程图如图8所示。

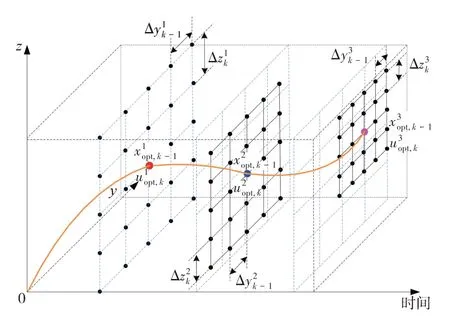
图6 迭代动态算法最优轨迹获取

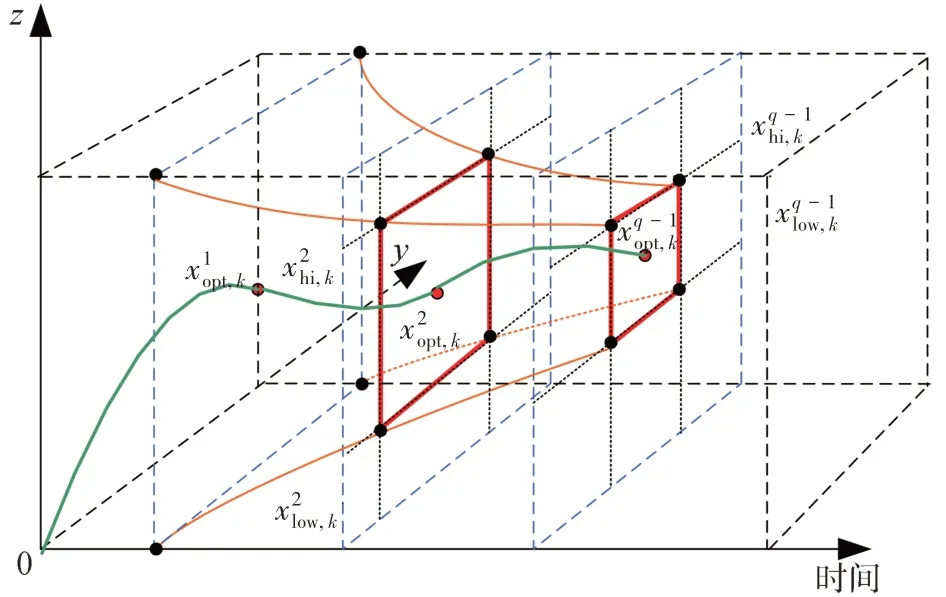
图7 迭代动态算法边界收敛图

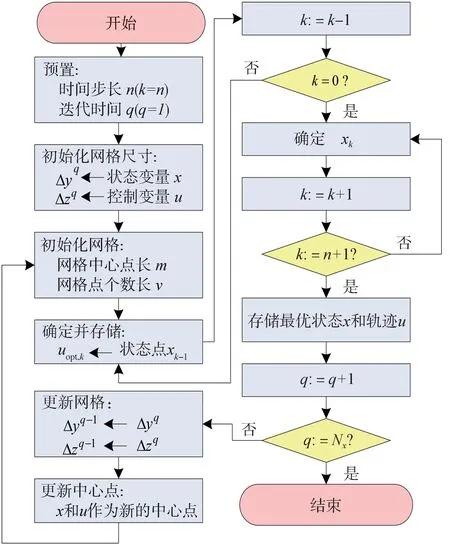
图8 迭代动态规划算法流程图

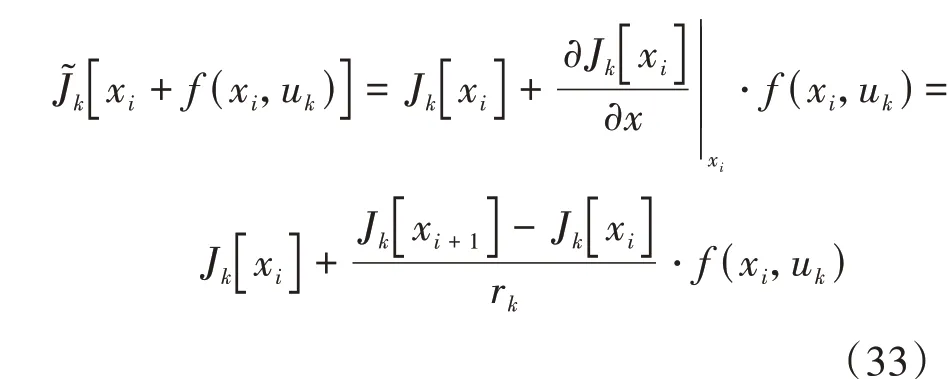
设状态变量迭代次数为，衰减因子为，则最优轨迹的上下边界表示为

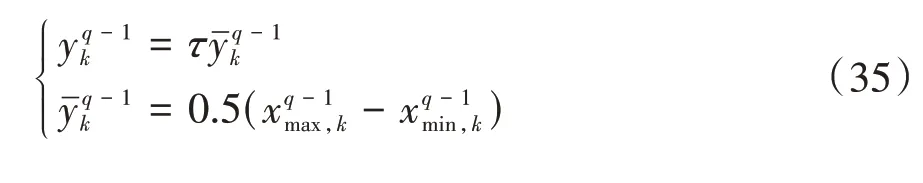
3 电池组热管理系统IDP 优化策略验证

通过Matlab-AMESim 联合仿真验证IDP 优化策略的有效性，针对温度对电池的影响确定温度的代价函数，以最小能耗作为性能指标，冷却液流速作为系统控制量，电池温度作为状态量。锂离子电池初始温度设为313 K，冷却液初始温度设为298 K，目标温度设为303 K。分别在恒流3C 和合成工况下对比PID 算法和DP 算法的优化效果。热管理系统电池组IDP冷却优化策略设计框图如图9所示。

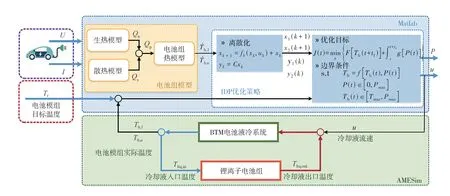
图9 IDP冷却优化策略设计框图

3.1 电池组温度性能对比

在恒流3C 下，传统PID 方法经过多次调试确定、、的参数，当= 0.1、= 0.0001、= 0.1时，得到较好的控制效果。通过仿真，得到1 号模组和7 号模组在PID 算法、DP 算法和IDP 算法下的电池温度如图10 所示，温度曲线的响应参数值见表2。

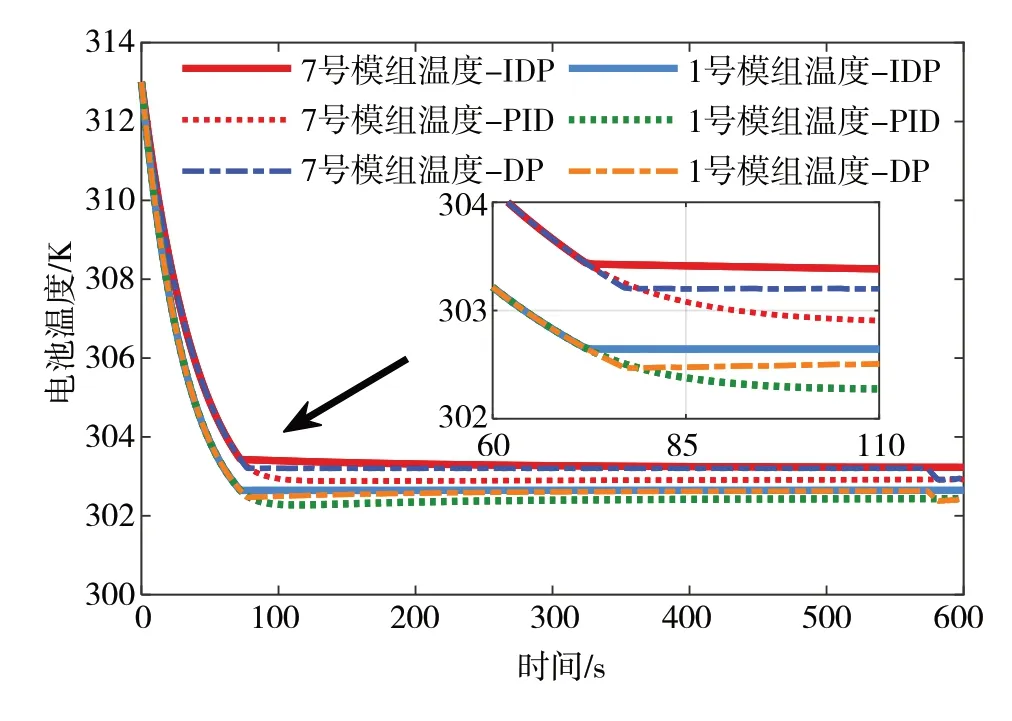
图10 恒流3C下温度结果对比

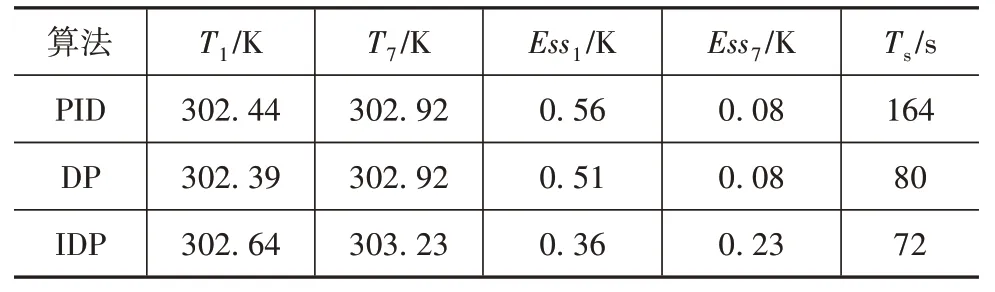
表2 恒流3C温度曲线的响应参数

通过图10 可以看出，在初始72 s 内冷却效果无明显差别。随着电池生热不断增加，IDP 优化策略最快做出反应。通过PID 算法得到的稳定时间是167 s，通过DP 算法的稳定时间为80 s，而在IDP 算法下仅为72 s。结果表明，本文提出的优化策略稳定时间更快，可更好地减少过多的冷却耗能。

为研究IDP 优化策略的抗干扰性，在合成工况下对其优化性能进行验证。由于本系统没有考虑空调回路等负载，故选取测试中其余负载均处于关闭状态的一个NEDC 工况和两个US06 工况合成一个2 383 s 的测试工况（U_N_U 工况）去验证实际的优化性能，其车速与电流如图11 所示。设置传统PID参数为= 0.05、= 0.001、= 0.01 时，控制效果最好。在整个工况下通过对比，1号电池模组与7号电池电阻的温度如图12 所示，6 条温度曲线的反应参数值见表3，可以看出，与PID 算法和DP 算法相比，IDP 算法误差和超调量最小，稳定时间也是3 种方法中最快的，仅仅为55 s。结果表明，以终端电池来看，本文提出的优化策略将温度稳定时间提高了76.49%，最大温度误差减小了52.79%，且超调量减小了53%。通过图13 可以看出，在不同循环测试下电池组最大温差始终保持在2 K 以内。综上，基于IDP 的优化策略冷却速率更快，最终值更接近目标温度。

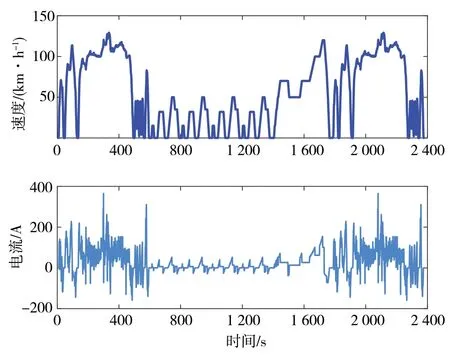
图11 U_N_U 合成工况车速与电流

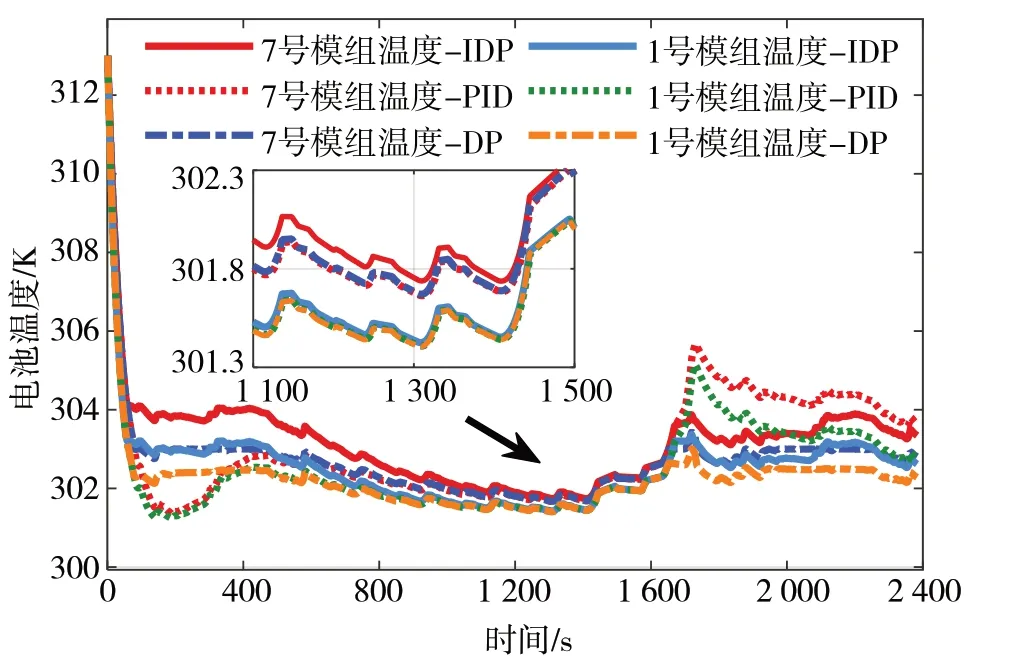
图12 U_N_U工况下温度结果对比

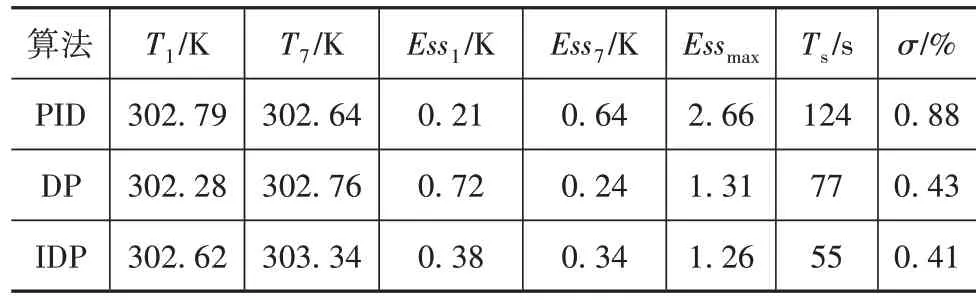
表3 U_N_U工况温度曲线的响应参数

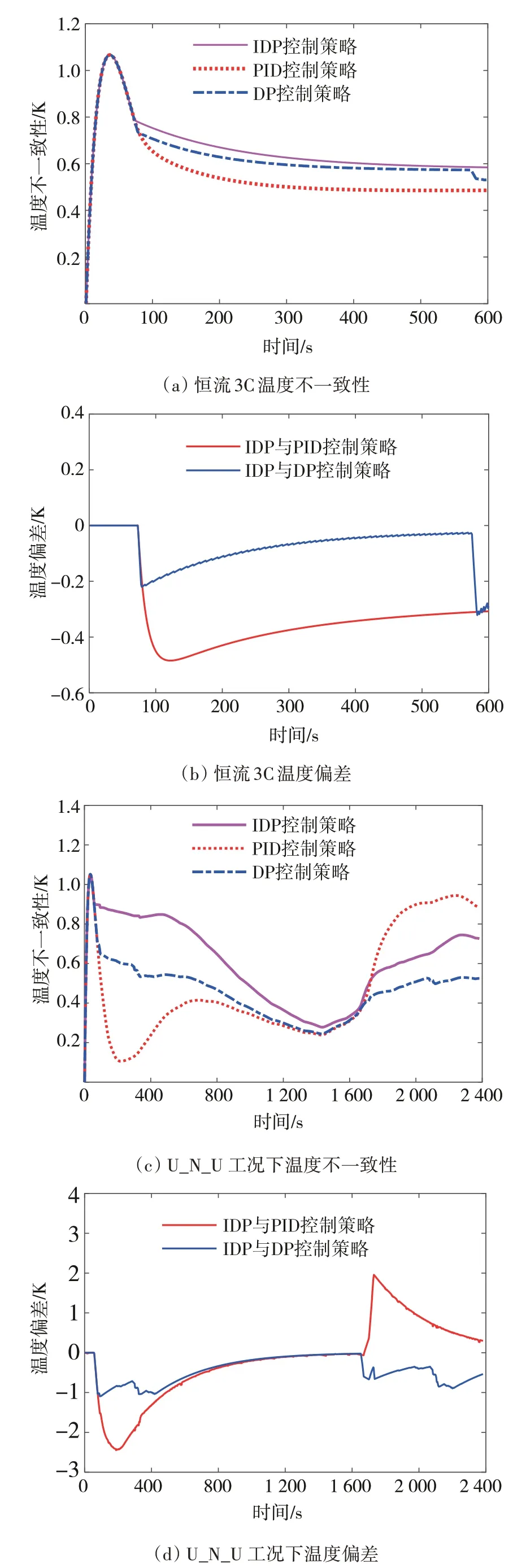
图13 恒流3C和U_N_U 工况下温度不一致性与偏差

3.2 冷却液流速与系统能耗结果对比

为验证IDP 优化策略能有效减少能量消耗，在恒流3C 下得到冷却系统的冷却液流速与系统能耗对比曲线，如图14 所示。并分别取图中对应时间点计算3 种方法下的瞬时能耗进行对比，如图15（a）所示。

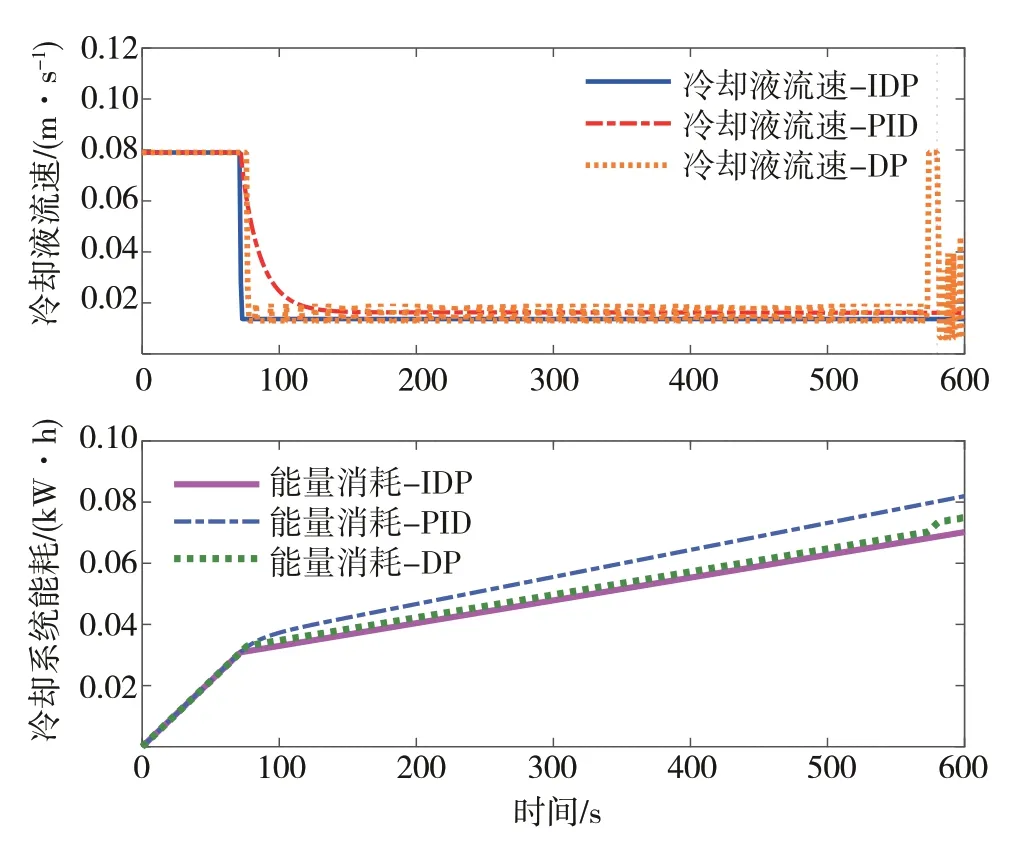
图14 恒流3C冷却液流速与能量消耗对比

仿真结果表明，在=72 s 前3 种方法的能耗相同，但是IDP 算法下的流速变化最快，而且稳定后的流速低于PID 方法下的冷却液流速。由于DP 算法略慢于IDP 算法，且流速稳定后有明显震荡现象。因此，随着能量消耗的累计，由图15可以看出在3种方法中，基于IDP 优化策略的能量损耗的全程累积趋势低于其他两种方法，且计算整个测试周期下的能耗结果显示，本文中提出的基于IDP 优化策略的能耗为252.39 kJ，比传统PID 方法下294.74 kJ的能耗降低了14.35%，比基于DP 方法的能耗降低了6.41%，减小能耗的优势较为明显。

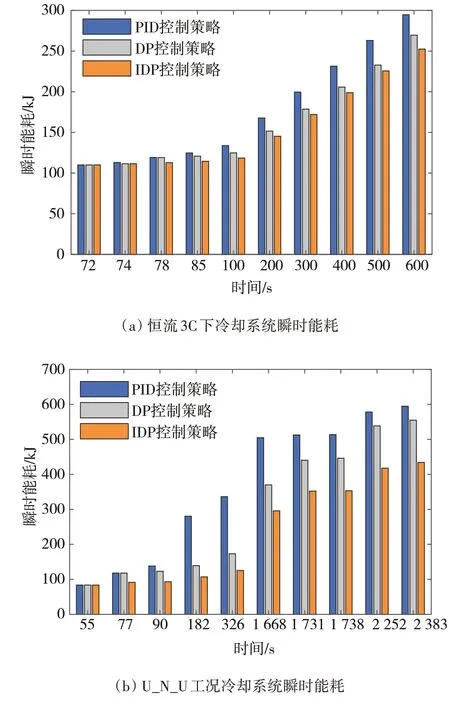
图15 恒流3C和U_N_U工况下冷却系统瞬时能耗

从U_N_U 工况下的流速与能耗的仿真结果（图16）可以看出，本文提出的方法具有良好的适应性。在=55 s 之前，3 种方法下的能耗几乎无差，基于IDP 算法下的冷却液流速在=55 s 时发生变化，而DP 方法和PID 方法下的冷却液流速以最大流速分别维持到了77 和193 s，直到=239 s 流速下降到相同值。流速的差值直接导致能量累积的不同，在U_N_U 工况下，经过低速运行后，如图16中所示，车速在=1637 s时开始加速，引起电流激增，导致电池的生热率也发生变化。由于电池的温度是一个累积量，所以导致冷却液流速发生了31 s的延迟，流速在=1668 s 时变大进行电池的降温。而从能耗上看，由于能量消耗是之前时刻值的叠加，所以能量有变化但波动不大。图15（b）中对应点瞬时能耗与恒流3C的结果相似，随时间的增加，基于IDP方法的能耗与另外两种方法下能耗差值也呈不断增大的趋势。

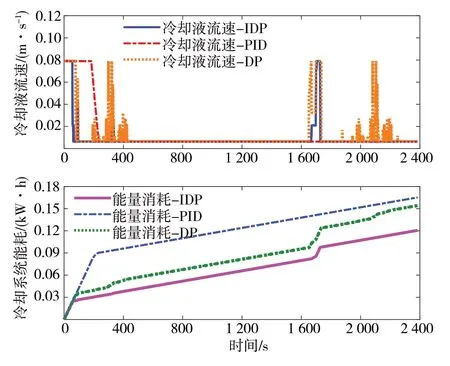
图16 U_N_U工况冷却液流速与能量消耗对比

在整个测试周期，基于IDP 方法的能量损耗为433.98 kJ，比PID方法下的594.53 K降低了27%，比基于DP 方法下的能耗降低了22%，如图17 所示。以上结果表明，基于IDP 优化策略在不同工况下都能更快地将电池温度稳定在目标温度附近，且能很好的减少能量损耗。

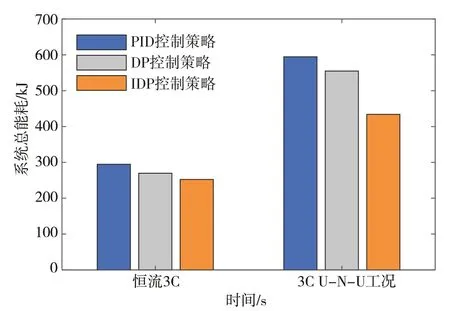
图17 冷却系统总能耗

4 结论

由于汽车行驶的实际工况十分复杂，加速、制动、上下坡等操作将带来复杂多变的动态负载，导致动力电池的散热需求增加。针对目前热管理系统中侧重电池的温度控制会导致系统能量过度损耗的问题。本文中提出了IDP 优化策略，以能耗最小为目的，使动力电池工作在最适合的温度范围。首先，建立了锂离子电池组集中质量热模型，在不同工况下与AMESim 中建立的动力电池液冷系统模型的输出进行对比，两者之间最大温差小于0.7 K，证明了模型的准确性。其次，将IDP 优化策略应用于锂离子电池组热模型，在恒流3C 和U_N_U 工况下，与PID方法和DP方法结果进行比较。仿真结果表明，本文中提出的基于IDP 优化策略在测试工况中，不仅大大缩短了温度调节时间，减小了稳态误差和超调量，而且总能耗降低了27%和22%，为系统节省了大量电能。结果表明，IDP 优化策略在具有高效性的同时，大大降低了冷却系统的能量损耗。本文被控对象针对电池冷却回路，没有考虑空调冷却回路和驾驶舱冷却回路，忽略了3 个回路的相互影响，只将负载所带来的影响归结至整车电流的波动中，将在后续研究中考虑3者之间的耦合关系。