公路弃土场边坡的稳定影响因素敏感性分析
2022-06-07丁文洁马祥配彭永和别凤华杨超解露茜
丁文洁,马祥配,彭永和,别凤华,杨超,解露茜
(山东省第八地质矿产勘查院,山东地矿局有色金属矿找矿与资源评价重点实验室,日照地质地理信息大数据研究院,日照市土地质量评价与污染修复重点实验室,山东 日照 276826)
0 引言
随着我国经济建设的加快,基础设施建设不断加强。在公路建设中由于受道路运输等条件的限制,不可避免的会产生大量弃土弃渣,因而,在公路建设时必然要设置一定的弃土场来满足弃土处置的需要[1]。
公路弃土场由于其欠固结、多孔隙、非饱和等结构特点[2],在降雨及动力荷载的影响下极易发生失稳滑坡[3]。研究弃土场边坡的稳定性,可以尽可能减小弃土场的潜在破坏性,对避免由于弃渣产生次生灾害、减少水土流失具有重要意义。在弃土场的选址、支挡措施等设计中就可有针对性地采取相应的措施,达到安全、经济和有效的目的。
目前,我国针对公路弃土场开展的研究很少。谭鹏[4]分析了弃土场失稳破坏机理并研究提出了弃土场稳定性分析方法,沈明祥[5]通过现场调查和计算分析评估了贵州省六盘水至威宁高速公路弃土场稳定性,郑鹤丹[6]运用Geo Studio软件对弃土体边坡稳定性进行了评估,分析正常工况和非常工况条件下弃土体边坡的稳定性,李研[7]对高速公路弃土场的处置方案进行了研究。以上文献从分析机理、现场调查、计算分析、风险评价、处置方案设计等方面研究了高速公路弃土场的相关问题,但均缺乏稳定影响因素敏感性的分析。因此,在实际工作中,有必要结合具体工程实例对高速公路弃土场进行稳定影响因素敏感性分析,预防地质灾害的发生。
公路弃土场在填筑过程中,需要根据弃土场的用途、稳定性,以及综合经济性等多种因素确定压实控制标准。本文以日照市岚山区某弃土场为例,通过MIDAS GTS NX进行数据模拟,在不同压实控制标准的情况下,归类分析高度和坡度对边坡稳定性系数的变化规律,从而找到边坡失稳的敏感因素。
1 敏感性分析原理
影响边坡稳定的因素有坡角、坡高、黏聚力、内摩擦角、含水率、重度以及地震、降雨等,各因素对边坡失稳的破坏程度是不同的,因此,通过边坡稳定影响因素的敏感性分析,可以找出影响弃土场边坡稳定的敏感因素,分析影响边坡稳定性各因素与边坡安全系数之间的相关性,即分析各因素的变化对于边坡安全系数的影响程度[8]。
敏感性分析是系统分析中对系统稳定性的一种不确定性分析方法[9-10]。
本文通过MIDAS GTS NX进行模拟,计算出不同条件下的安全系数,然后选取任意一个影响因素在可能范围内变化,且保持其他影响因素不变来计算安全系数,最后计算各影响因素的敏感性。
2 弃土场现状
日照市岚山区某弃土场,坡脚距实验小学边坡坡顶约10m。整个弃土场坡面平缓,坡面未见滑坡,坡顶未见裂缝、坍塌现象,整个坡面完整性好。
弃土场堆土岩性为素填土,最大厚度约6.0m,中密,湿,成分以回填风化岩碎屑为主;其下为残积成因砂质黏性土,硬塑状;底部为晋宁期花岗片麻岩,强风化,变晶结构,片麻状构造,主要成分为石英、长石及其他暗色矿物,岩体呈致密的砂砾状及角砾状(图1)。坡顶植被不发育。
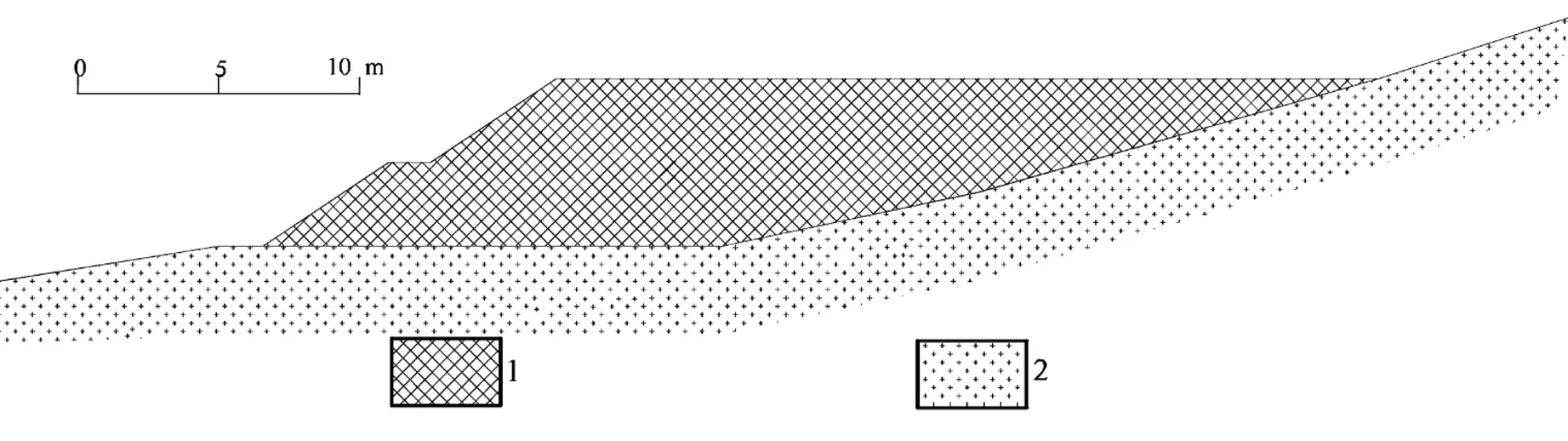
1—填土;2—强风化花岗岩图1 弃土场剖面图
3 建立基本模型
3.1 建模
本文根据实际的边坡坡面形态、各岩层岩性及其物理力学特征构建模型[12-14]。采用MIDAS-GTSNX软件中的有限元强度折减法(SRM)[15-18]算出边坡的等效应变塑性区及安全系数,以此分析边坡稳定性。
模型分为两个部分,分别是弃土场基底区A和弃土区B(图2、图3、图4),图中单位为m,计算时线网格控制间距0.5m。
约束条件:模型左右两侧为水平约束,底部固定,上部及坡面为自由边界。
本构模型:根据土体的应力应变特性,选取本构模型为Mohr-Coulomb模型。
初始应力:仅考虑自重应力产生的应力场。
计算收敛标准:收敛误差小于定值10-6,最大迭代次数1000次,计算终止。重力加速度选取9.80665m/s2,几何误差0.0001。
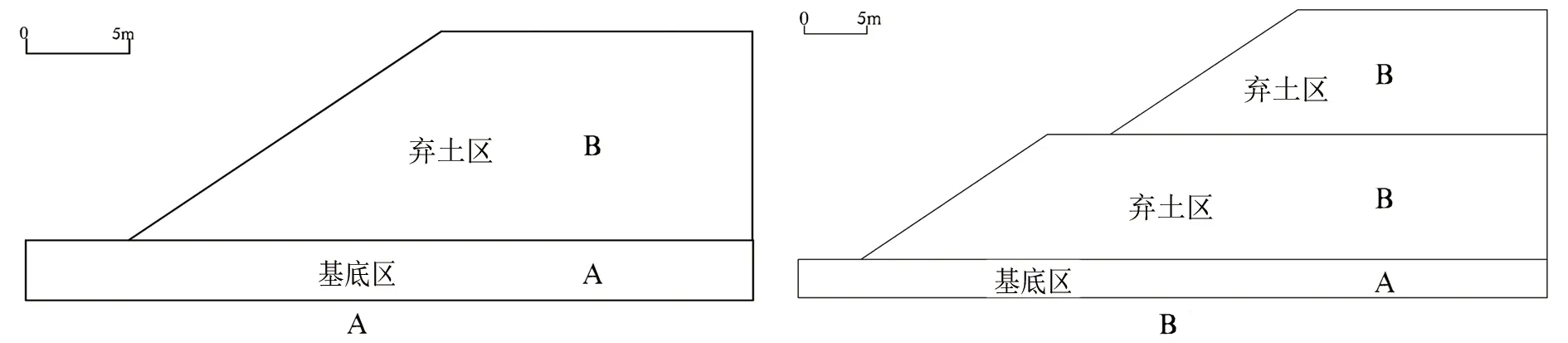
图2 一级边坡二维模型(A)二级边坡二维模型(B)
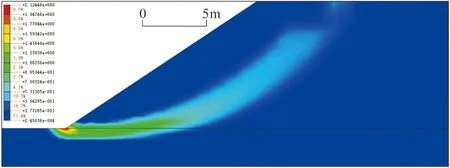
图3 一级边坡剖面等效应变云图
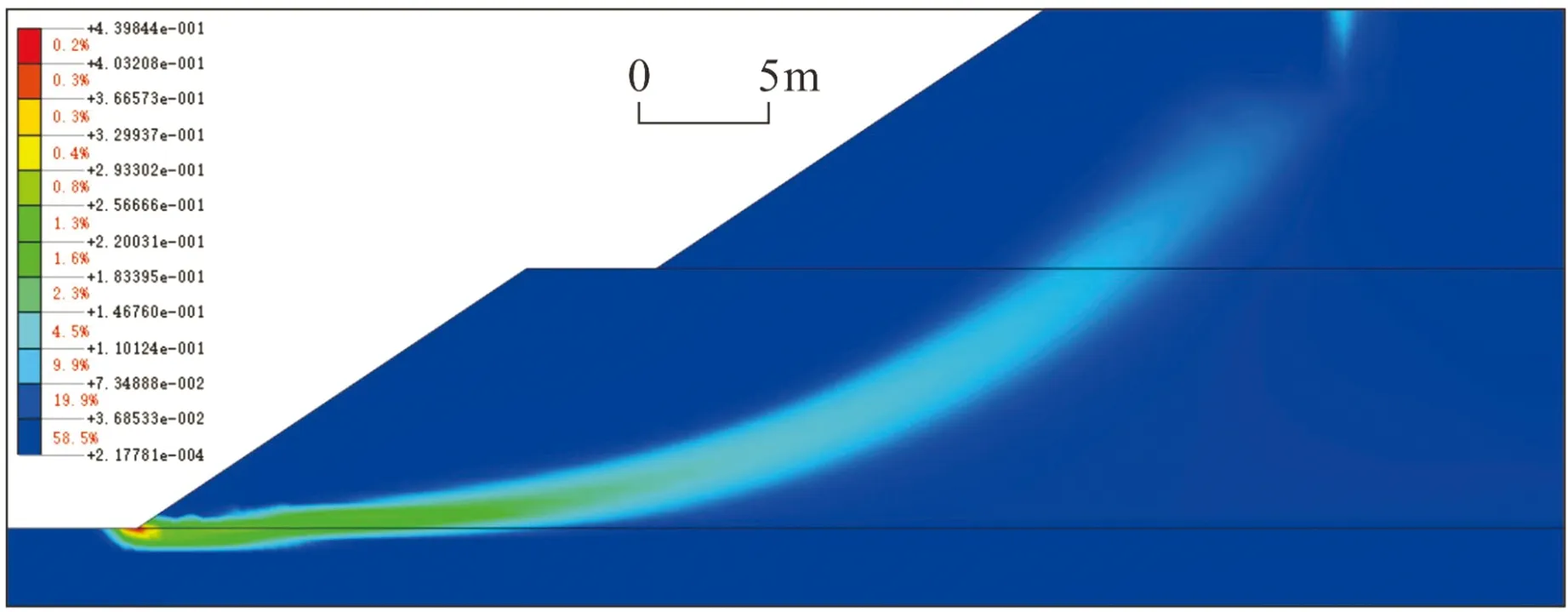
图4 二级边坡剖面等效应变云图
3.2 软土强度参数试验
堆放于弃土场的土主要为坡积粉质黏土,开展了直剪试验[19],得到了不同压实度下的黏聚力、内摩擦角值和容重值(表1)。
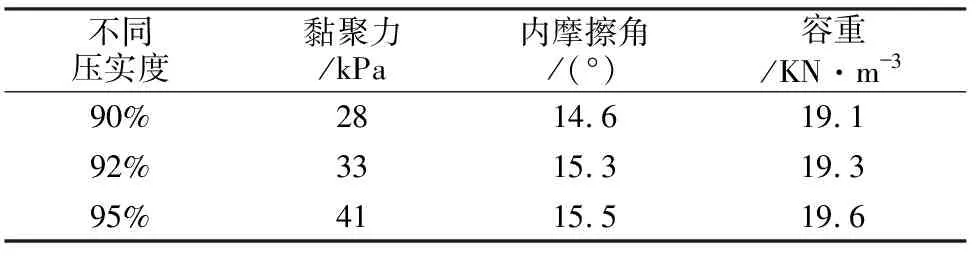
表1 直剪试验结果一览表
4 模拟计算
根据前人[20]对工程边坡进行过的研究,整理总结并通过现场工程地质勘查分析,影响边坡稳定性的因素有很多[21],主要影响因素有坡脚角度、边坡高度、岩(土)体的抗剪强度性指标内摩擦角和岩(土)体的黏聚力[22]。压实度决定了岩(土)体的抗剪强度性指标内摩擦角和岩(土)体的黏聚力,本文主要分析在不同压实控制标准的情况下,研究坡脚角度、边坡高度对边坡稳定性系数的影响。
本文采用控制变量法[23]来探究边坡稳定性,运用MIDAS GTS NX进行安全系数计算。假设该边坡为均质土层,在不同压实控制标准的情况下,选取不同的坡角β、坡高H,来获得不同的安全系数,并对获得的稳定系数进行分析。
(1)压实度为90%时,黏聚力为28kPa,内摩擦角为14.6°,坡高分别选取5m、6m、7m、8m、9m、10m,坡比分别选取1∶0.5、1∶0.75、1∶1.00、1∶1.25、1∶1.50,得到相应的安全系数,详见表2、表3。
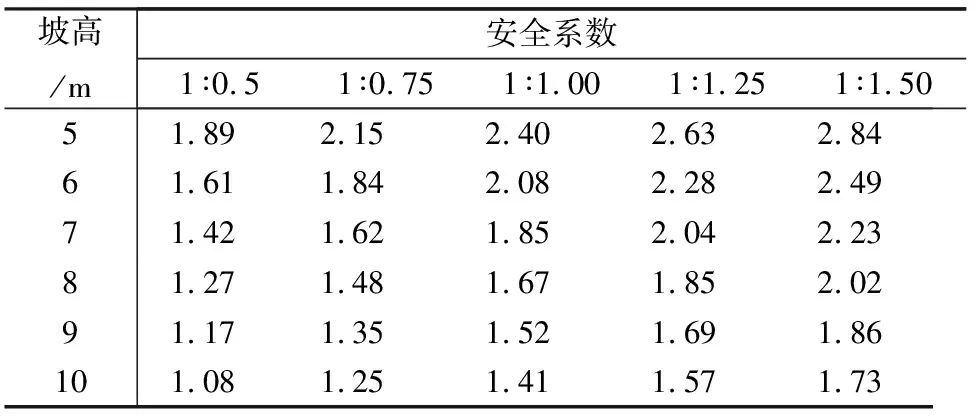
表2 90%压实度下不同坡高、坡比对应的安全系数(一级坡)
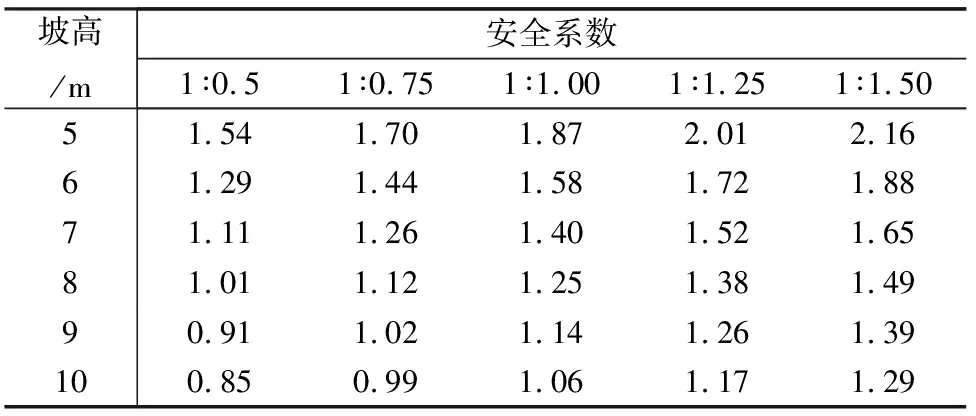
表3 90%压实度下不同坡高、坡比对应的安全系数(二级坡)
(2)压实度为92%时,黏聚力为33kPa,内摩擦角为15.3°,坡高分别选取5m、6m、7m、8m、9m、10m,坡比分别选取1∶0.5、1∶0.75、1∶1.00、1∶1.25、1∶1.50,得到相应的安全系数,详见表4、表5。
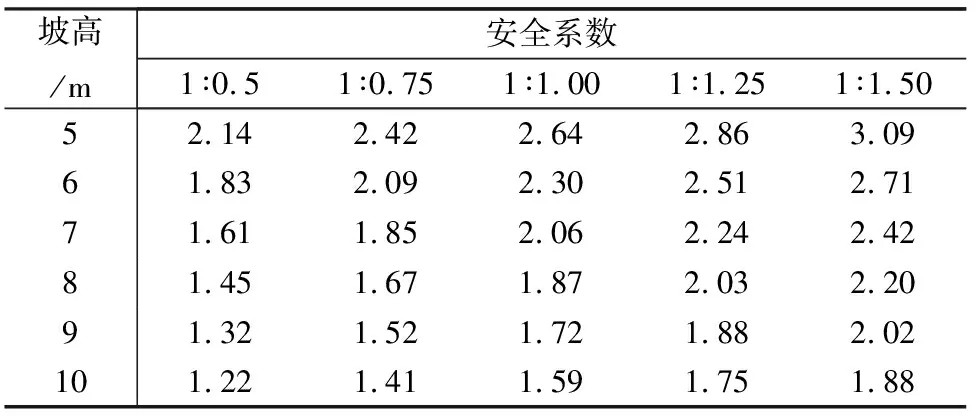
表4 92%压实度下不同坡高、坡比对应的安全系数(一级坡)
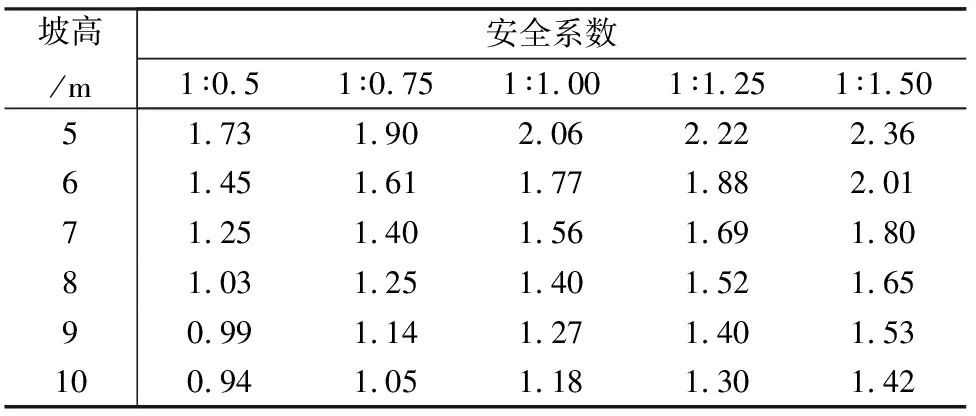
表5 92%压实度下不同坡高、坡比对应的安全系数(二级坡)
(3)压实度为95%时,黏聚力为41kPa,内摩擦角为15.5°,坡高分别选取5m、6m、7m、8m、9m、10m,坡比分别选取1∶0.5、1∶0.75、1∶1.00、1∶1.25、1∶1.50,得到相应的安全系数,详见表6、表7。
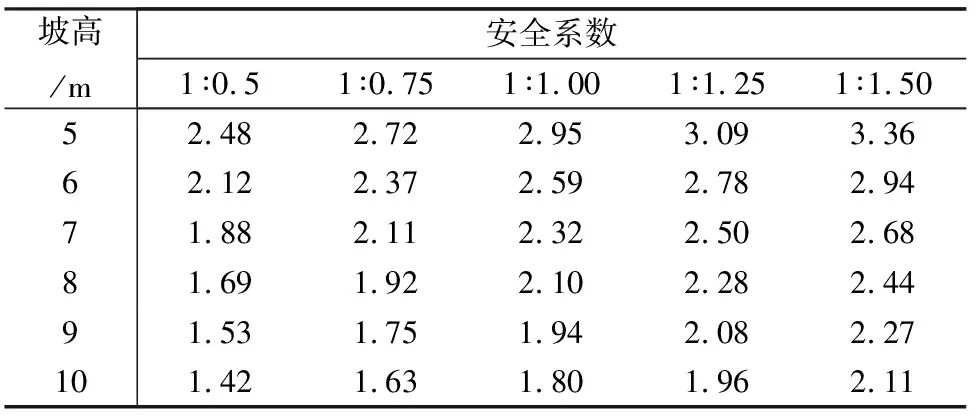
表6 95%压实度下不同坡高、坡比对应的安全系数(一级坡)
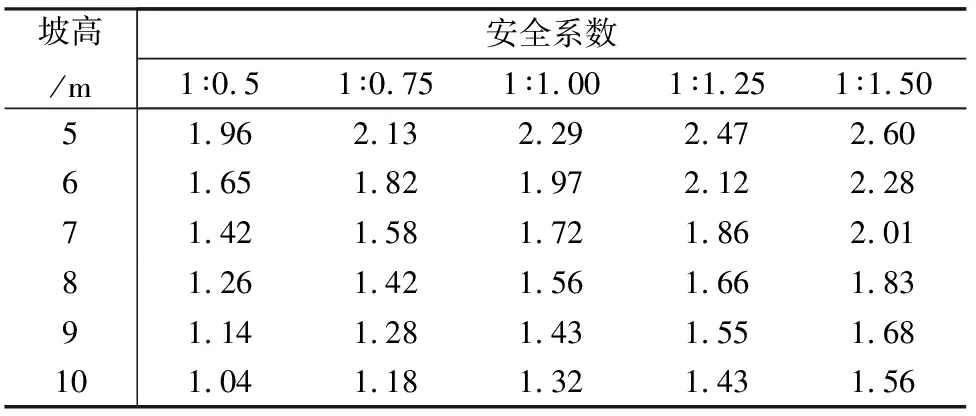
表7 95%压实度下不同坡高、坡比对应的安全系数(二级坡)
5 边坡稳定性影响因素的敏感分析
公路弃土场在填筑过程中,已经根据实际需要确定了压实控制标准。由于不同压实控制标准决定了岩(土)体的内摩擦角和黏聚力,所以本次工作选取在不同压实控制标准的情况下,改变坡高H、坡角β,进行影响因素的敏感分析。
5.1 边坡高度的敏感性分析
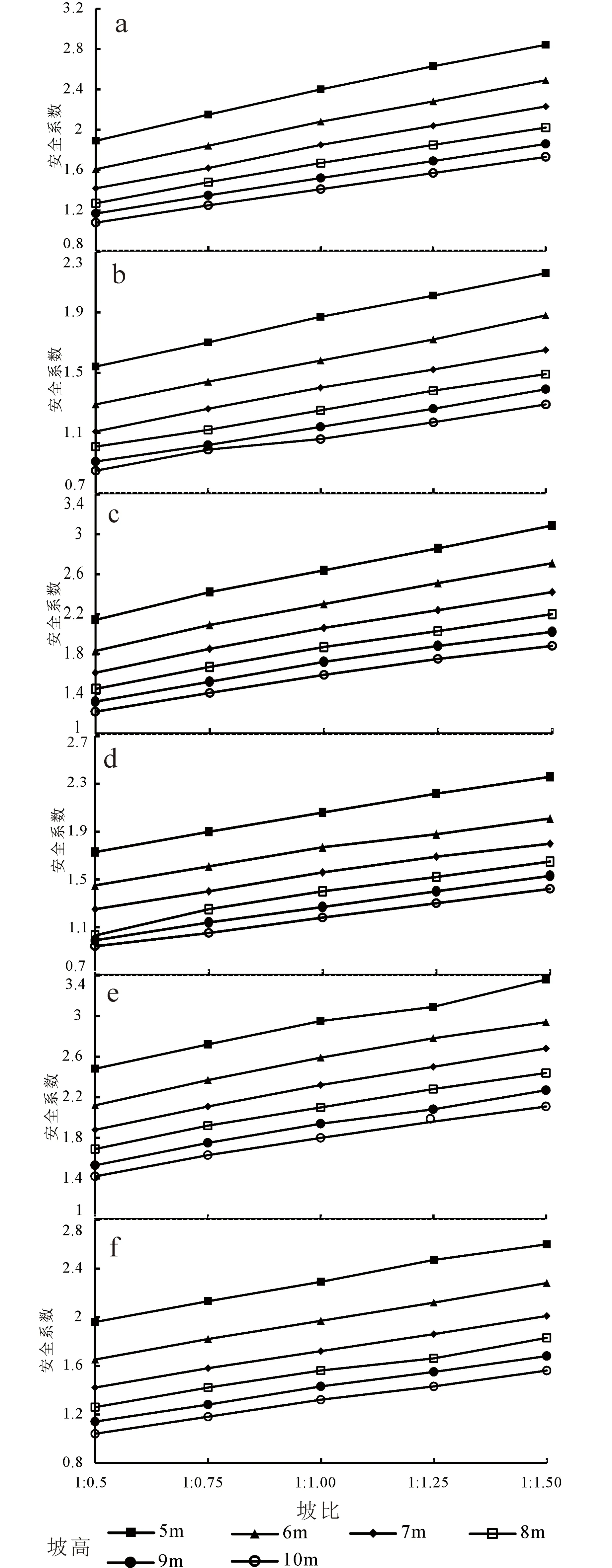
利用数值模拟的结果(表2—表7),绘制坡高H与安全系数的关系图(图5)。通过图5知,在相同的坡比下,坡高与安全系数呈向上凹的抛物线关系,且随着坡高的增加,边坡安全系数在不断减小。坡高在5~7m范围逐渐增大时,边坡安全系数降低很快;在坡高在7~10m之间增大时,安全系数降低速率相较于稳定性系数在5~7m范围内的变化要小。
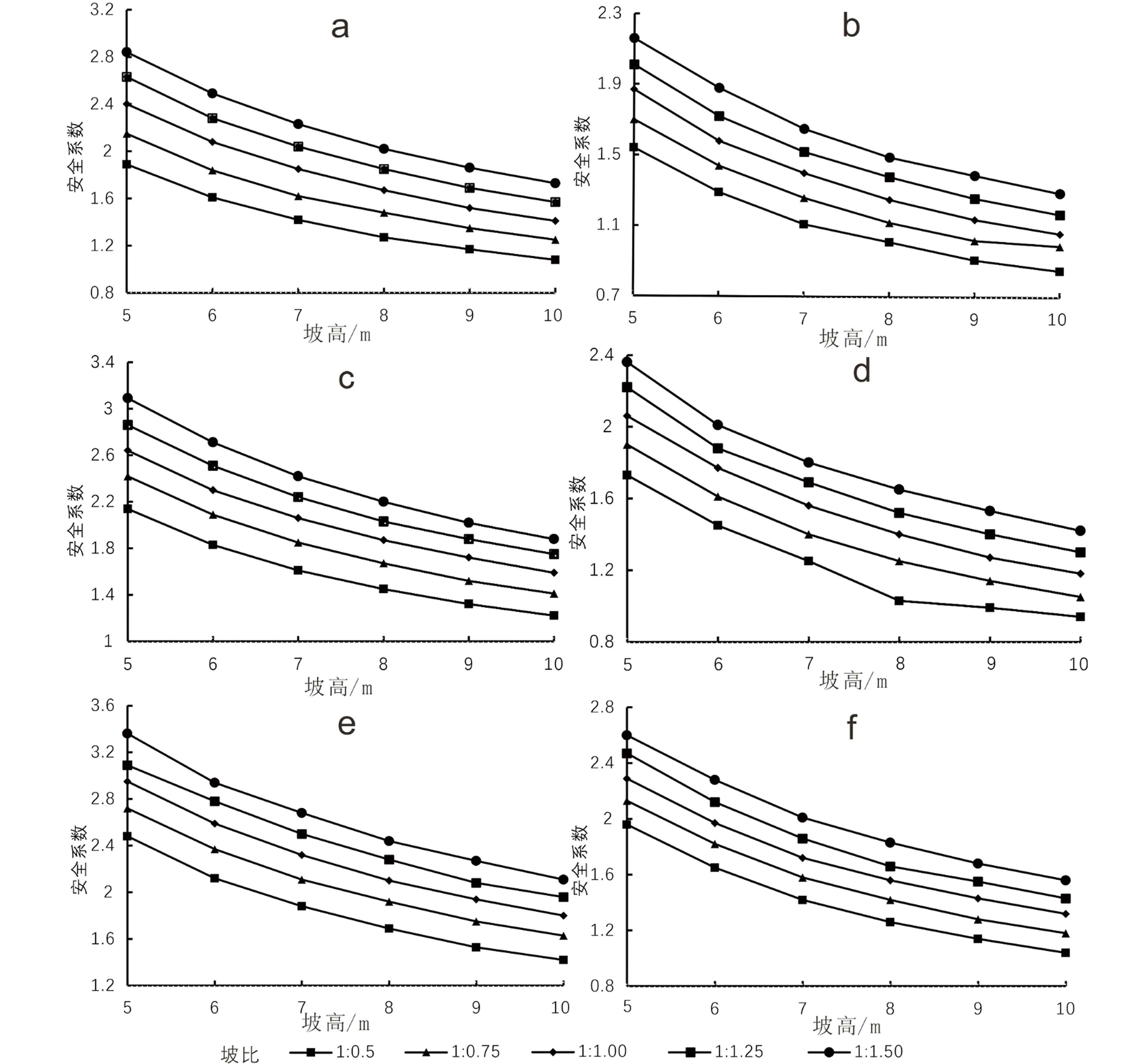
a—90%压实度一级坡坡高与安全系数关系图;b—90%压实度二级坡坡高与安全系数关系图;c—92%压实度一级坡坡高与安全系数关系图;d—92%压实度二级坡坡高与安全系数关系图;e—95%压实度一级坡坡高与安全系数关系图;f—95%压实度二级坡坡高与安全系数关系图图5 不同类别下坡高与安全系数关系图
根据敏感度原理,计算出不同类别下弃土场坡高的敏感度,例如:90%压实度一级坡,坡比为1∶0.5,当高度从7m减少到5m(降低约为28.57%)时,安全系数由1.42增加至1.89(增加约为33.10%),弃土场坡高的敏感度约为1.158,而高度从7m增加到10m(增加约为42.86%)时,安全系数由1.42减小至1.08(降低约为23.94%),弃土场坡高的的敏感度约为0.559。各个类别下的敏感度计算如表8。
(1)弃土场边坡高度下降敏感度数值远大于边坡高度上升敏感度数值,由此可以得出:弃土场边坡高度下降对安全系数影响比弃土场边坡高度增加对安全系数影响敏感。
(2)随着坡比的减小,无论边坡高度下降还是增加,坡高对安全系数的影响有减小的趋势,即说明随着坡比的减小,边坡高度的变化对稳定性的影响在减小。
(3)相同条件下,压实度越大,无论坡高减小还是增加,坡高对安全系数的敏感度有下降的趋势,说明压实度越大,边坡高度对安全系数的影响在减小。
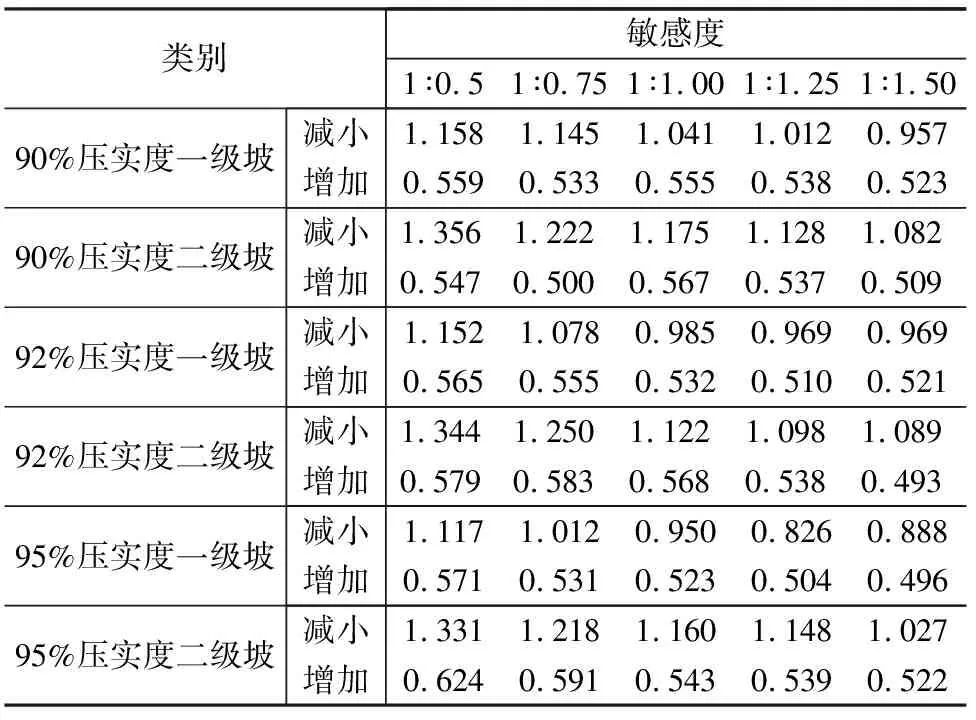
表8 弃土场坡高敏感度统计表
5.2 边坡坡比的敏感性分析
利用数值模拟的结果(表2—表7),绘制坡比与安全系数的关系图(图6)。通过图6知,在相同的高度下,坡比与安全系数呈一定的线性关系,且随着坡比由1∶0.5变化到1∶1.5,边坡安全系数在不断增大。
(1)弃土场坡比减小敏感度数值大于坡比增加敏感度数值,由此可以得出,弃土场坡比减小对安全系数影响比弃土场坡比增加对安全系数影响大。
(2)随着高度的增加,无论坡比增加还是减小,坡比对安全系数的敏感度呈增加的趋势,说明随着高度的增加,坡比对安全系数的影响在增大。
根据敏感度原理,计算出不同类别下弃土场坡比的敏感度,例如:90%压实度一级坡,坡高为5m,当坡比从1∶1.00增加到1∶0.50(增加约为100%)时,安全系数由2.40减少至1.89(减少约为21.25%),弃土场坡高的敏感度约为0.213,而坡比从1∶1.00减小到1∶1.50(减小约为33.33%)时,安全系数由2.40增加至2.84(增加约为18.33%),弃土场坡高的敏感度约为0.550。各个类别下的敏感度计算如表9。
(3)在相同高度下,压实度越大,无论坡比增加还是减小,坡比对安全系数的敏感度减小,说明相同高度下,压实度越大,坡比对安全系数的影响减小。
a—90%压实度一级坡坡比与安全系数关系图;b—90%压实度二级坡坡比与安全系数关系图;c—92%压实度一级坡坡比与安全系数关系图;d—92%压实度二级坡坡比与安全系数关系图;e—95%压实度一级坡坡比与安全系数关系图;f—95%压实度二级坡坡比与安全系数关系图图6 不同类别下坡比与安全系数关系图
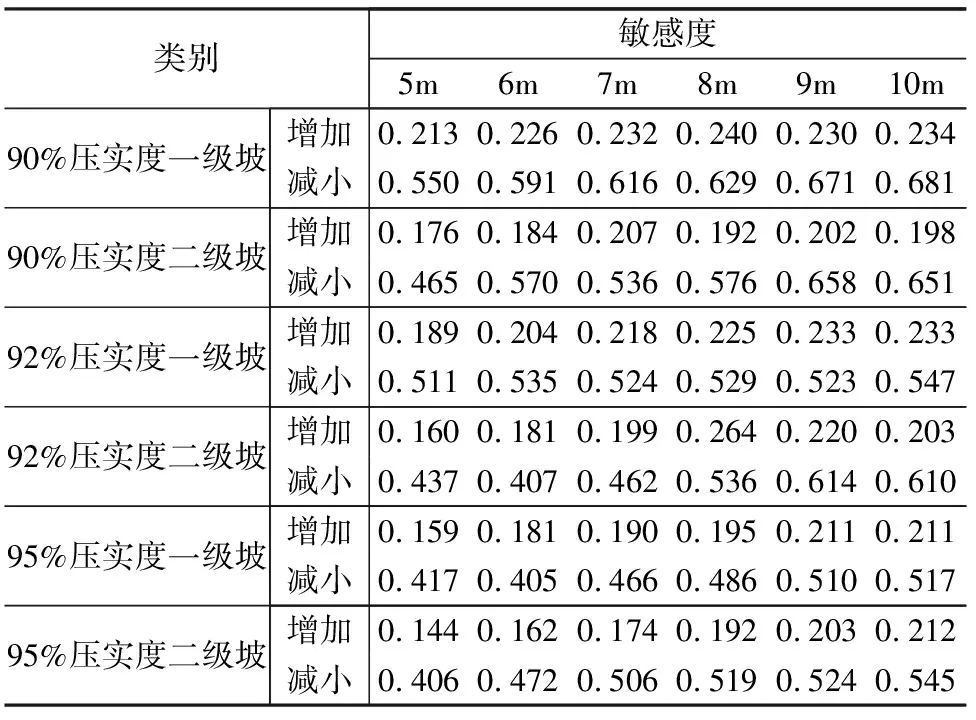
表9 弃土场坡比敏感度统计表
6 结论
利用MIDAS GTS NX软件,对压实度分别为90%、92%、95%,高度为5~10m,以及坡角为1∶1.50~1∶0.50的一级坡和二级坡进行了模拟,系统的对边坡稳定性进行了分析。利用控制变量法,分析了在坡高和坡比单独变化下边坡的稳定性。利用敏感度,分析了在不同压实控制标准下,坡高和坡比对安全系数的影响。以下为本文的主要结论:
(1)弃土场边坡高度下降比弃土场边坡高度增加对安全系数影响敏感;弃土场坡比减小比弃土场坡比增加对安全系数影响敏感。
(2)随着坡比的减小,边坡高度的变化对稳定性的影响在不断减小;随着高度的增加,坡比的变化对安全系数的影响增大。
(3)相同条件下,压实度越大,边坡高度和坡比对安全系数的影响越小。
