基于差分进化-模糊PID的风电机组变桨复合控制策略
2022-06-07邵宜祥胡丽萍黄俊杰
邵宜祥,刘 剑,胡丽萍,过 亮,方 渊,黄俊杰
(南瑞集团有限公司,南京 211106)
0 引言
大型变速变桨风力发电机组(以下简称“风电机组”)运行在额定风速以上大多采用PID(比例积分微分)变桨距控制方式[1-3],通过调整桨叶的桨距角,改变气流对叶片的攻角,从而改变风电机组的风能捕获率,使其输出功率保持稳定。由于风速变化随机性较大,PID 控制往往不能保证系统的鲁棒性。为了改善风电机组运行性能,文献[4]提出了一种预报-校正变桨控制策略,该控制策略在高风速时可以降低变桨动作频率,改善风电机组运行性能;文献[5]提出了一种新型的异步变桨控制策略,有效地减少了风轮转矩的波动;文献[6]提出将模糊控制与Smith 预估补偿控制相结合构成模糊Smith预估控制方法,实现了风电机组的恒功率控制,但未考虑初值对PID控制器的影响;为了实现对桨距角进行精确调整并使输出功率快速稳定到额定值附近,文献[7-8]提出了基于自抗扰控制器的变桨控制策略,具有较快的响应速度及较好的抗扰动能力。文献[9]提出了基于模糊控制的变速变桨控制方法,虽然模糊PID 控制可以动态地调节PID 控制器参数,提供系统对扰动的适应性,但模糊PID 控制器属于反馈控制器,具有时滞性,只有当系统出现误差时,控制器才开始工作。为此,文献[10]提出了一种有效风速估计的前馈与传统PID反馈结合的变桨距控制策略,前馈控制[11-12]可以动态补偿桨距角,通过前馈控制给出相应的桨距角前馈值,以提前修正桨距角,提高系统响应速度,但是其忽略了PID 控制器的初始参数对系统的影响。
本文提出了一种基于DE(差分进化)-模糊PID 的变桨复合控制策略,即前馈控制和DE-模糊PID 结合的控制策略。该控制策略中,反馈控制器采用模糊PID控制器,采用DE算法对PID初始参数进行优化,根据专家经验设计了模糊规则库,使PID 控制器参数可根据偏差和偏差变化率动态修正;将风速信号作为前馈引入控制系统中,实现桨距角动态补偿,以提高风速扰动下系统的响应速度。以2 MW 直驱风电机组为研究对象,以DE-模糊PID 控制和模糊PID 控制为参照,分别在湍流风、阵风及存在安装误差扰动、叶片弯曲扰动情况下,对控制系统的性能进行了仿真对比研究。仿真结果表明:相较于DE-模糊PID 控制和模糊PID 控制,本文所提复合控制策略可使风电机组的输出功率更稳定,对安装误差、叶片弯曲等扰动的抑制效果更好。
1 风电机组的气动特性
风力发电机的组成主要包括机械系统和电气系统结合空气动力学和贝兹理论的分析,风电机组从风能中捕获的机械功率为:
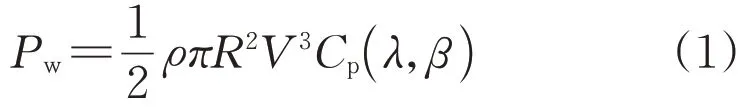
式中:ρ为空气密度;R为风轮半径;V为风速;β为桨距角;λ为叶尖速比,λ=,ωtur为风轮角速度;Cp(λ,β)为风能利用系数,其曲面如图1所示。
从图1可以看出,对于每一个桨距角,风能利用系数Cp(λ,β)都有一个最大值,该点对应的λ值就是最佳叶尖速度。当外界风速小于额定风速时,桨距角为定值。为了保持最大的风能利用率,应根据风速调整发电机转速,以达到最佳叶尖速度。当外界风速大于额定风速时,电机转矩和气动转矩不能平衡,应改变桨距角以保持风电机组稳定。
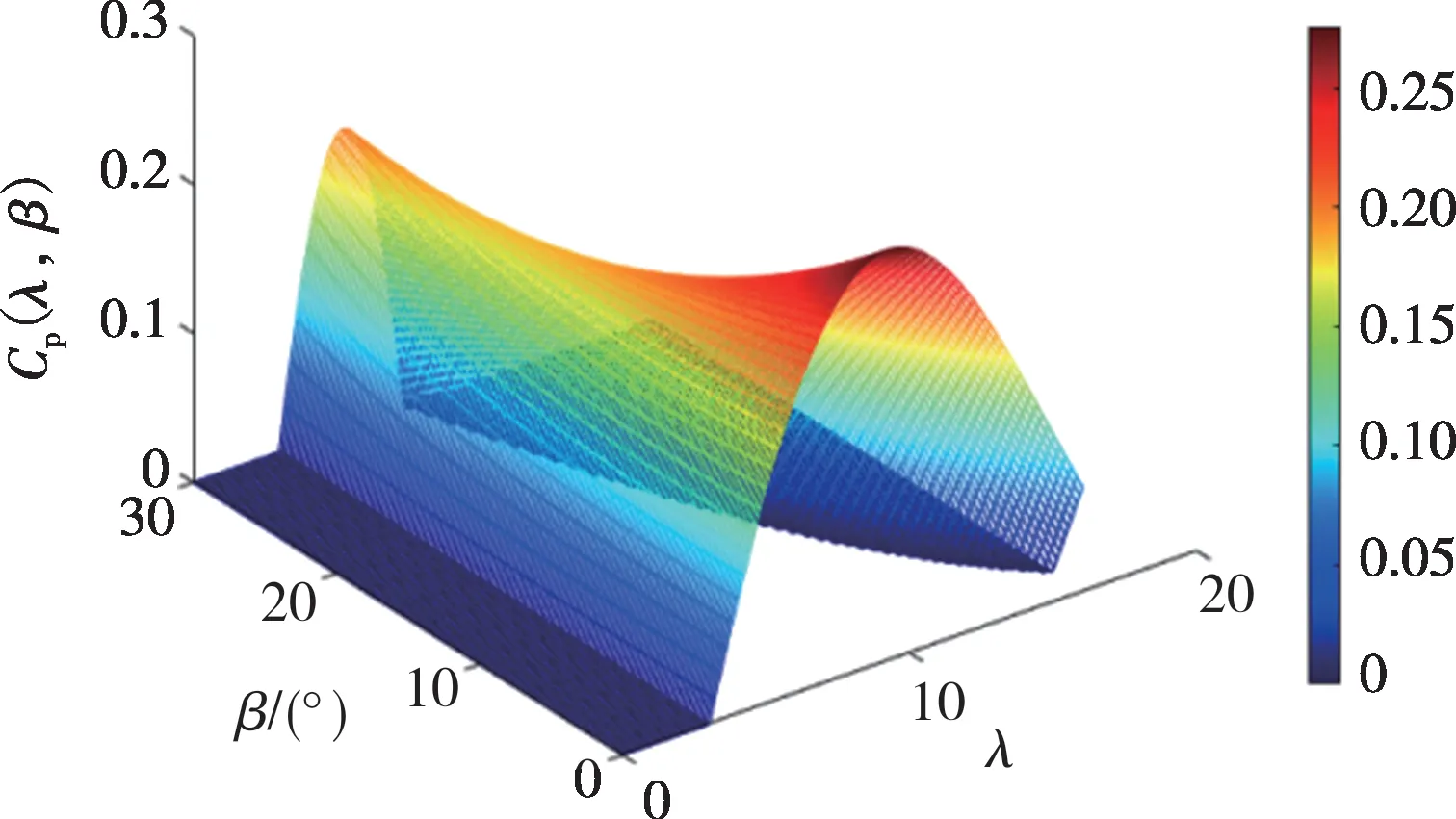
图1 风电机组的风能利用系数
2 变桨距风电机组的模型
2.1 传动系统模型
风电机组的传动链常通过如图2所示的两质量块模型进行模拟,将风轮和永磁同步发电机分别视为一个质量块,并通过柔性传动链将之连接。
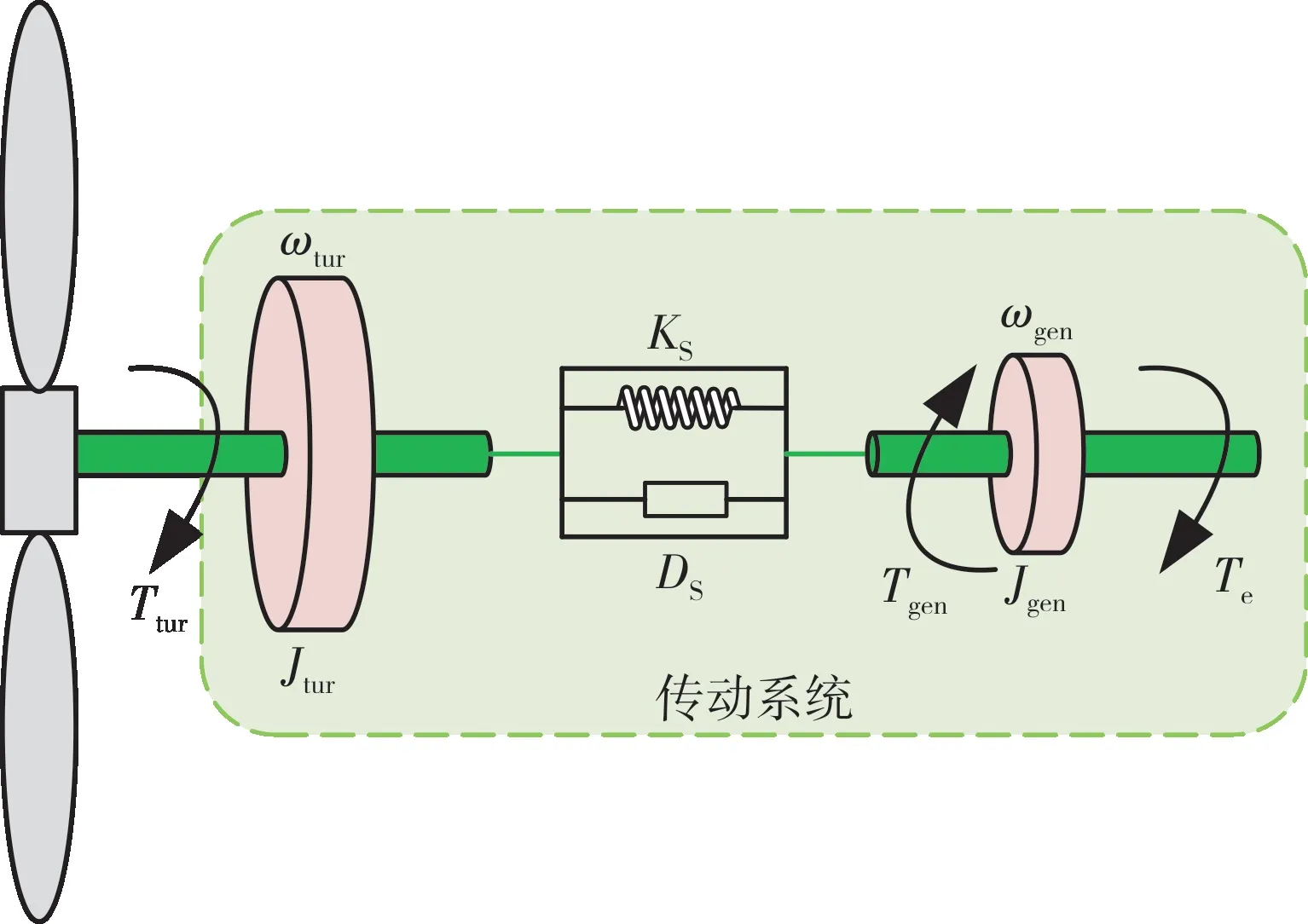
图2 风电机组传动系统两质量块模型
根据弹簧阻尼系统的动力学模型,传动系统的模型可以表示为:
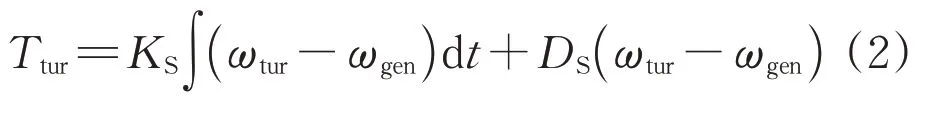
式中:KS和DS分别为传动系统的刚度系数和阻尼系数;Ttur为风电机组的转矩;ωgen为发电机转子的转速。
风电机组在气动力矩Ttur的作用下以一定的角速度运行。风电机组运动方程可表示为:
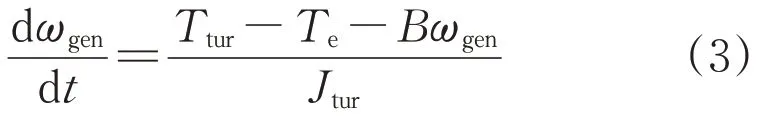
式中:B为电机转动粘滞系数;Te为电磁转矩;Jtur为风轮转动惯量。
2.2 永磁同步机的数学模型
以永磁转子磁极中心线为d轴,沿转子旋转方向超前d轴90°电角度为q轴,d-q坐标系随转子同步旋转。经过坐标变换后得到发电机在d-q坐标系中的数学模型为:
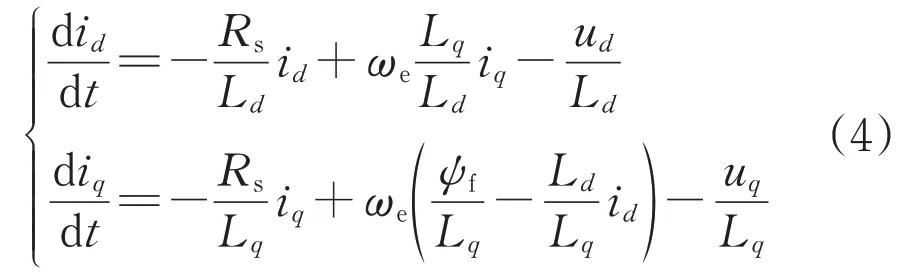
式中:u和i分别为定子电压和电流;下标d、q为经过坐标变换后的d、q轴分量;ωe为电角速度;Rs为定子电阻;ψf为永磁体磁链。
2.3 变桨系统模型
目前,液压驱动系统常被用于大型风电机组的变桨系统。因此本文采用一阶惯性连杆来模拟变桨执行器的动态特性,其表达式为:

式中:βref为桨距角给定值;Tβ为变桨执行器的时间常数,通常采用实际变桨距系统的运行数据确定Tβ。
3 DE优化算法原理
DE算法是一种基于种群进化的全局智能优化算法,利用种群个体间的差异引导个体变异,通过交叉和贪婪选择使适应度更高的个体保留至下一代,随着进化过程,种群逐步达到最优解状态。令xi(t)是第t代的第i个个体,则xi(t)=是搜索空间,N为种群规模。DE 算法的具体步骤如下:
1)生成初始种群,生成初始种群公式为:
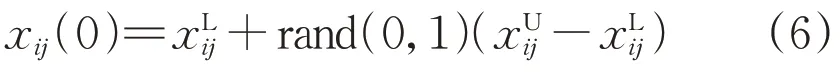
2)变异操作,生成变异个体的方法为:
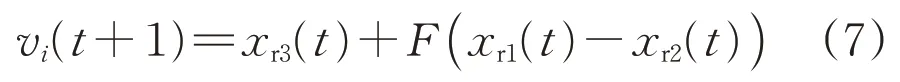
式中:vi(t+1)为第t+1 代变异个体;xr1、xr2、xr3为从种群中选取与当前个体不同且互不相同的整数;F为变异率,其控制差分量(xr1(t)-xr2(t))的放大和缩小。
3)交叉操作,其作用是增加种群的多样性,将变异生成的个体vi(t+1)和当前的个体xi(t)进行二项分布交叉操作,生成杂交个体ui(t+1),即:
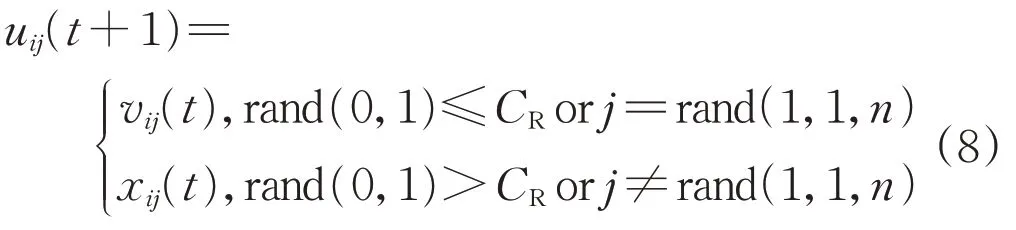
式中:CR为交叉概率,其范围为[0,1];rand(1,1,n)是[1,n]之间的一个随机整数。
4)选择操作,通过调用适应度函数对向量uij(t+1)和向量xij(t)进行比较,做出选择,如式(9)所示:
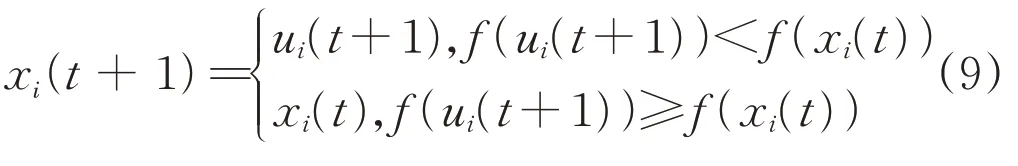
4 控制策略设计
本文所提的基于DE-模糊PID 的变桨复合控制策略框图如图3 所示。其中,βf(s)为桨距角前馈值,V(s)为风速,GF(s)为前馈控制器的传递函数,风速为前馈信号,用以动态补偿桨距角;模糊PID 控制器为系统的主控制器,PID 初始参数通过差分进化算法优化,并通过模糊规则对其动态修正。
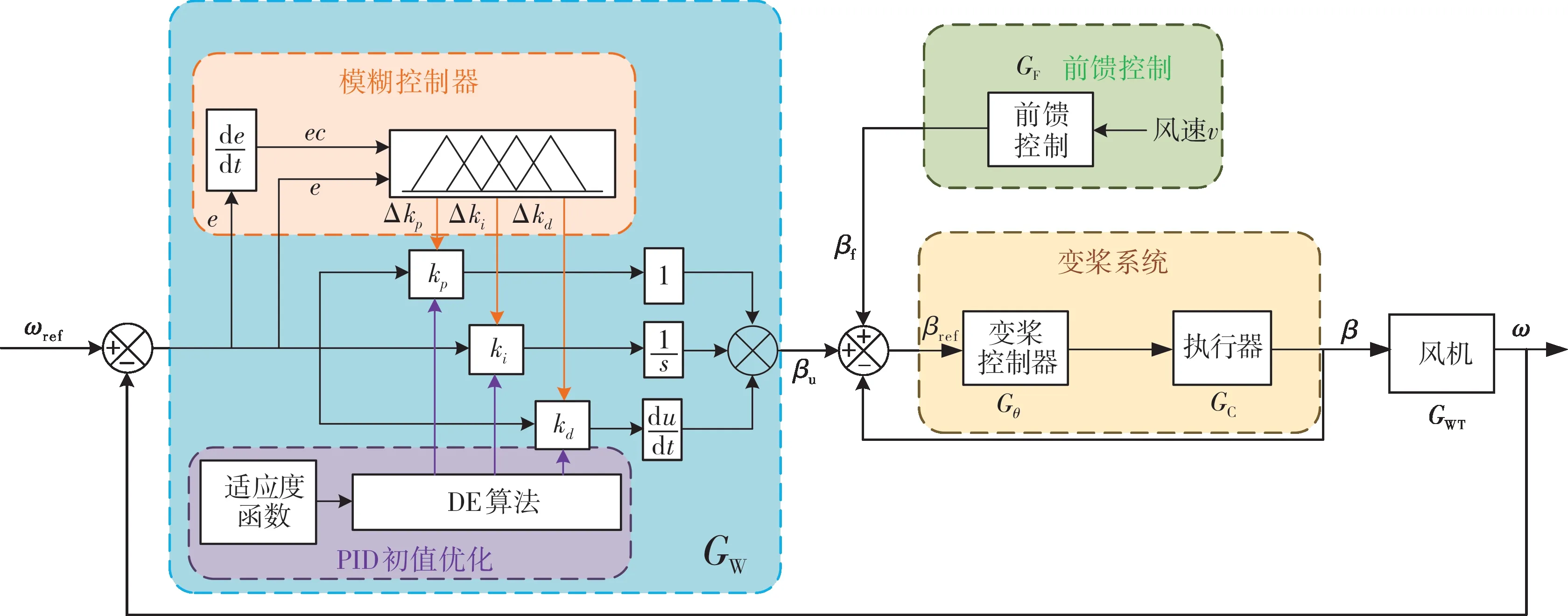
图3 基于DE-模糊PID的变桨复合控制框图
4.1 DE-模糊PID反馈控制器设计
传统的变桨PID 反馈控制能够在额定风速附近处取得良好的控制效果,但是在风机运行中,由于风速变化范围大、变化速度快,而常规PID由于控制参数固定,当外界风速变换较大时很难保证风机稳定运行。模糊控制具有良好的抗干扰能力,但模糊控制器在控制点附近容易出现盲区和死区导致稳态误差大。将模糊控制与PID 控制相结合,通过模糊控制对PID 参数进行动态修正可弥补两种控制器的缺点。PID初始参数kp0、ki0、kd0是影响控制系统性能的重要因素,若kp0、ki0、kd0选择不当,则会导致系统消除静差时间过长、静差过大、震荡次数过多甚至系统发散等问题,传统的工程整定方法很难达到理想的控制效果。DE 算法是一种基于种群进化的全局智能优化算法,因此,本文采用DE 算法优化PID 初始参数,以确保控制器性能。在本文中选择积分时间绝对误差作为适应度函数,其公式为:
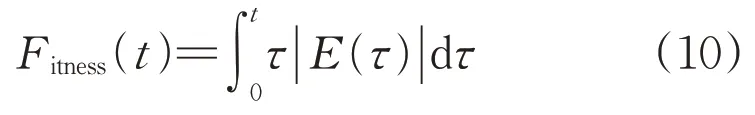
式中:E(τ)为风轮给定转速与实际转速的差值。具体优化步骤如下:
Step1:将PID控制器参数kp、ki、kd分量构成一个差分进化算法的个体,设置DE 算法参数,如:种群数N和放缩因子F。
Step2:根据式(6)随机产生初始化种群。
Step3:根据式(7)—(9)进行变异、交叉、选择操作。
Step4:判断是否是最大迭代次数,若是,则输出结果;若否,则转到Step3继续迭代。
模糊PID 控制器以误差E和误差变化率EC(dE/dt)作为控制器的输入,如图4 所示。模糊控制的输入和输出论域均为[-3,3]。模糊子集为{NB,NM,NS,ZO,PS,PM,PB}。NB和PB处采用高斯隶属度函数,其余采用三角隶属度函数。误差和误差变化率的隶属度函数如图4所示。
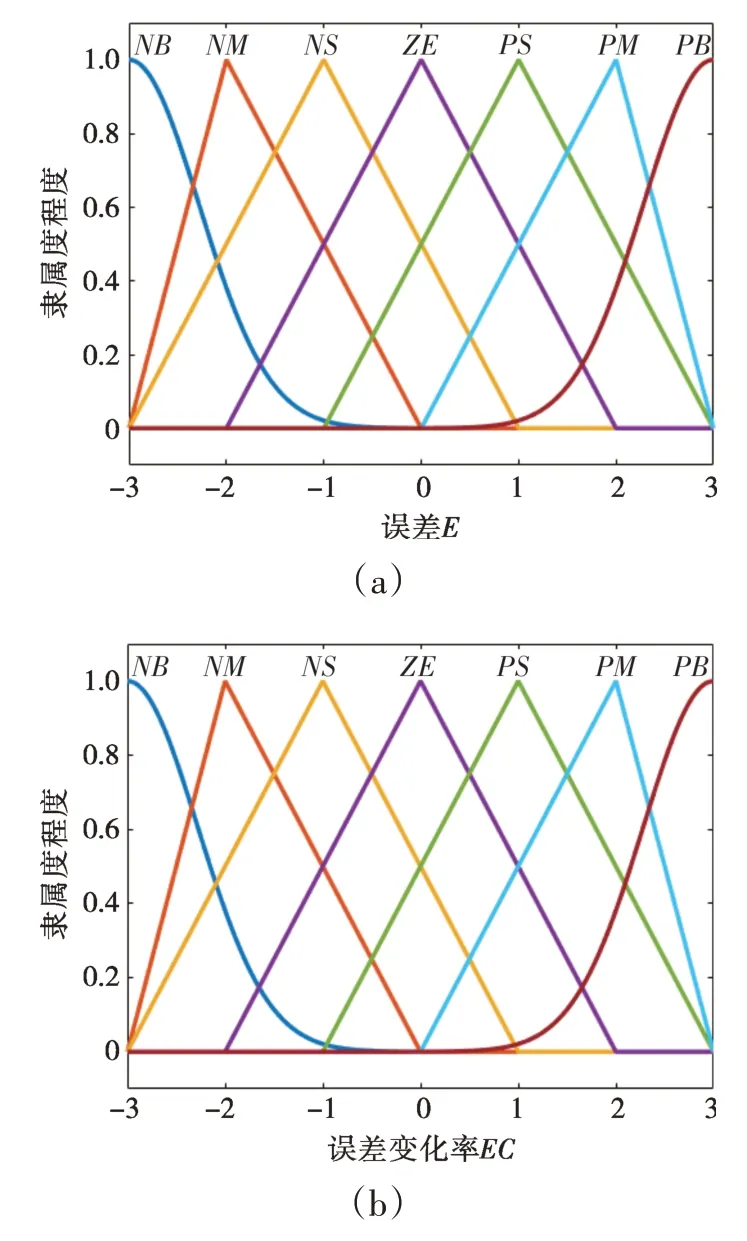
图4 模糊控制器输入量的隶属度函数
模糊控制器将输入量转化为相应的模糊变量值以实现模糊化,并根据制定的模糊规则对模糊输入做进一步模糊推理,解模糊后得到PID 控制器参数的修正量Δkp、Δki、Δkd。模糊控制器规则如表1所示。
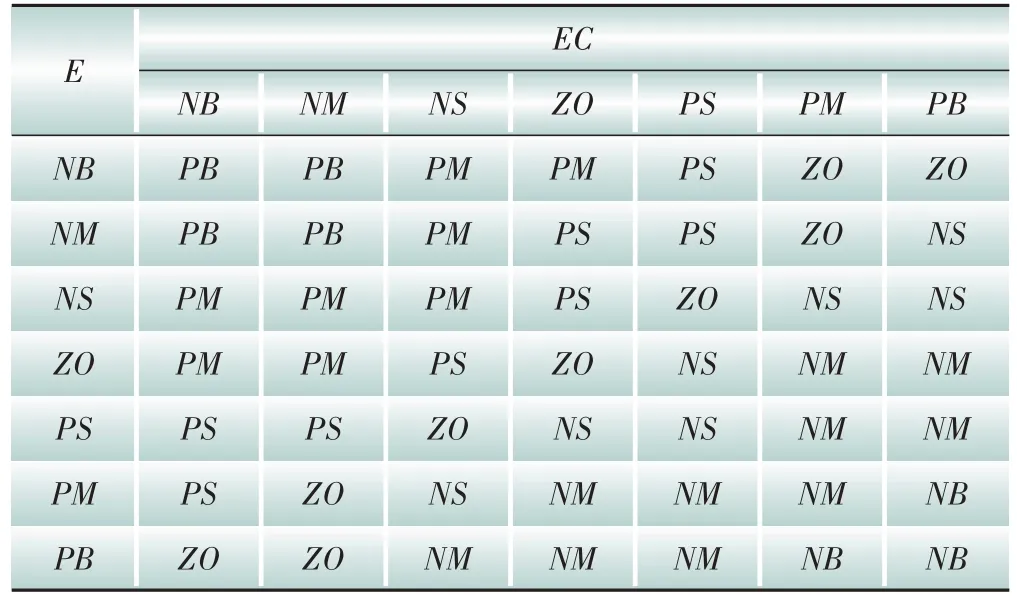
表1 模糊控制器的模糊规则
4.2 前馈控制器设计
前馈控制器将风速作为输入信号,输出桨距角前馈值以动态补偿桨距角,从而使风电机组的输出功率保持稳定。桨距角前馈值的大小与风速变化量呈正相关,即风速增大时,桨距角前馈值增大,桨距角随之增大,风能利用率下降;反之则桨距角前馈值减小,桨距角随之减小,风能利用率增大。
βf(s)、V(s)、GF(s)有如下关系:
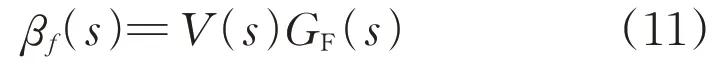
风轮转速ω(s)和βu(s)有如下关系:
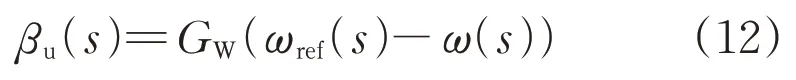
式中:GW为反馈控制器的传递函数;βu(s)为反馈控制器输出的桨距角值。
βu(s)与变桨系统的输出值β(s)关系为:
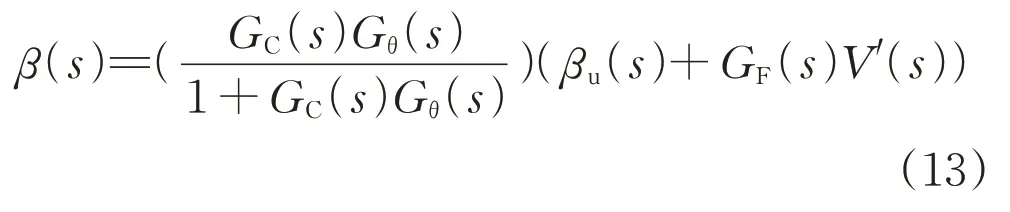
变桨系统输出值β(s)、实际风速V(s)与转速ω(s)的关系为:
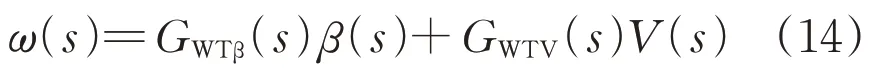
式中:GWTβ(s)为桨距角β(s)到风轮转速的传递函数;GWTV(s)为风速到风轮转速的传递函数。
通过式(11)—(14)可求解出前馈控制器传递函数为:
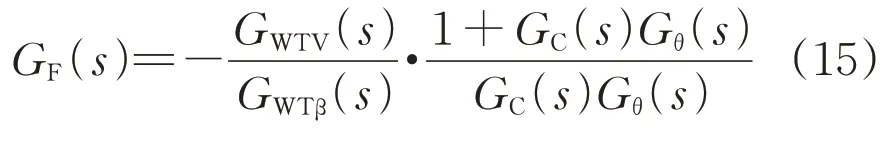
5 仿真分析
为了验证本文所提控制策略的有效性,通过仿真对比验证其性能,并通过施加不同扰动测试控制策略的抗扰性。仿真均基于一台2 MW 直驱风力发电机,其切入风速、额定风速和切出风速分别为3 m/s、11 m/s和22 m/s;风轮直径和高度分别为93.4 m和80 m;叶片长度为45 m;风轮额定转速为12.1 r/min。
1)在阵风工况下,基本风速为11 m/s,最大风速为14 m/s,风速曲线如图5所示,对比3种控制策略的效果。
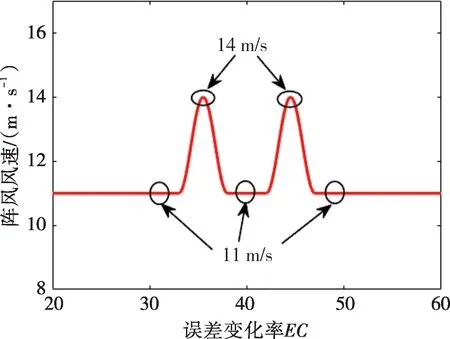
图5 阵风风速曲线
图6为阵风下的桨距角对比。其中,在34 s附近处风速增加和38 s 附近处风速减小,控制系统中有前馈控制时,桨距角变化幅度大于不加前馈控制的桨距角变化幅度。在DE-模糊PID控制下,桨距角的变化幅度也大于模糊PID 控制下桨距角的变化幅度。
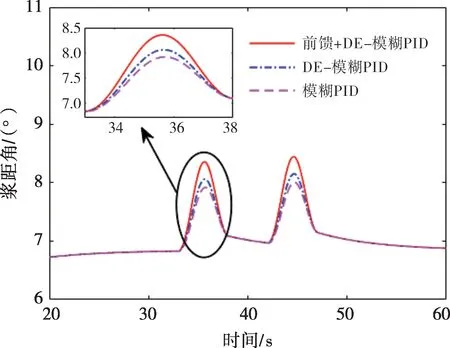
图6 阵风下的桨距角对比
图7和图8分别为阵风下的风轮转速和输出功率对比。在前馈控制的作用下,风轮转速和输出功率的波动幅度小于另外两种控制策略。在50 s附近处,在前馈控制下,风轮转速和输出功率可以更快地恢复到额定值。在模糊PID 控制下,经过DE优化控制的转速和功率波动幅度小于未经优化的,并且DE-模糊PID 控制下的转速和功率更接近额定值。
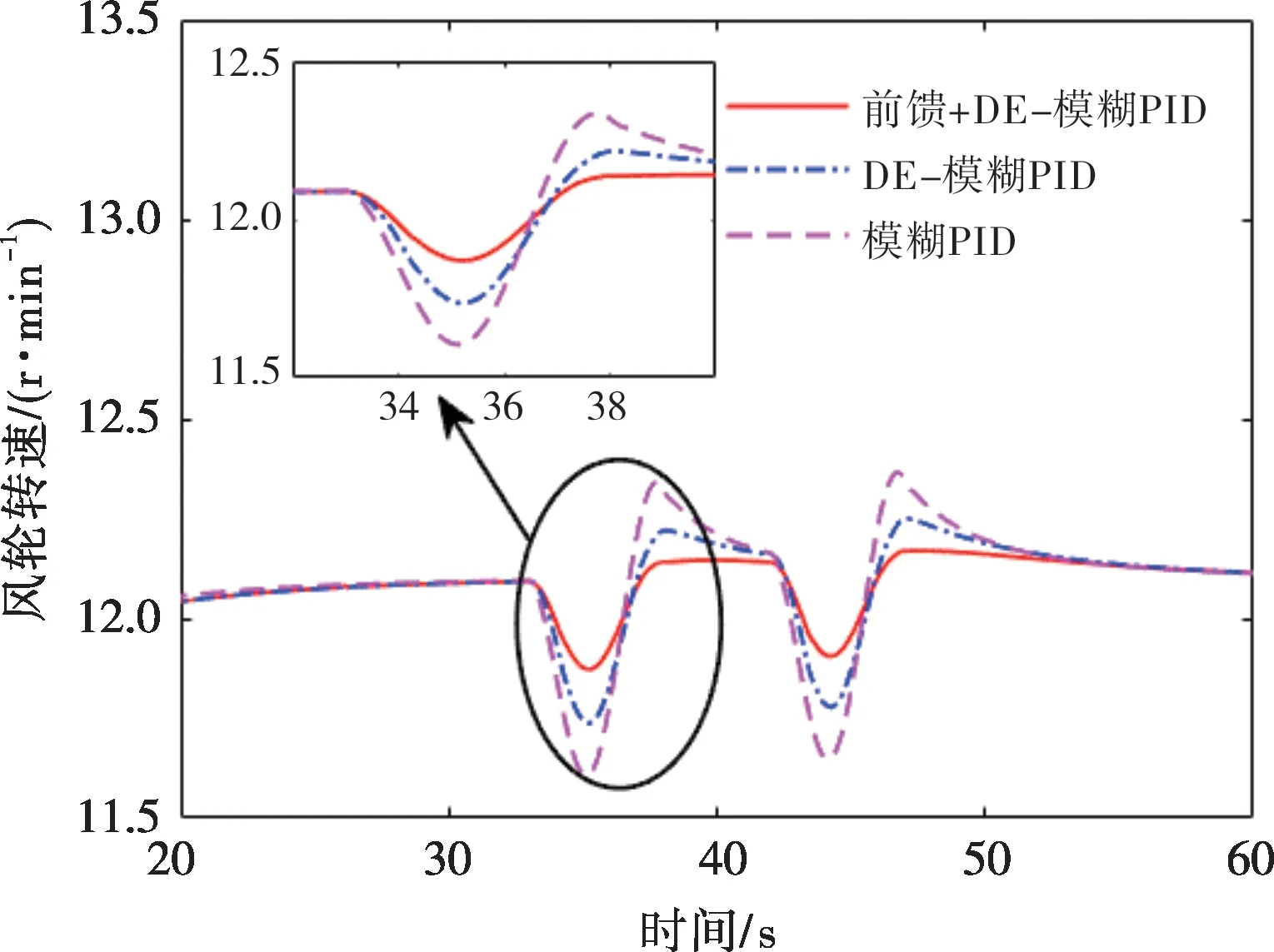
图7 阵风下的风轮转速对比
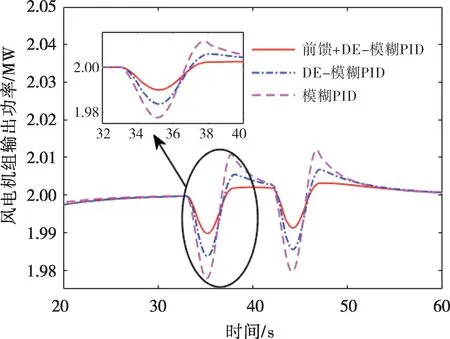
图8 阵风下的风电机组输出功率对比
2)在湍流风工况下,风速曲线如图9所示,平均风速为11 m/s,湍流强度为0.1,其在62 s附近处风速变化较大。对比前馈+模糊DE-PID控制、DE-模糊PID控制和模糊PID控制的效果。
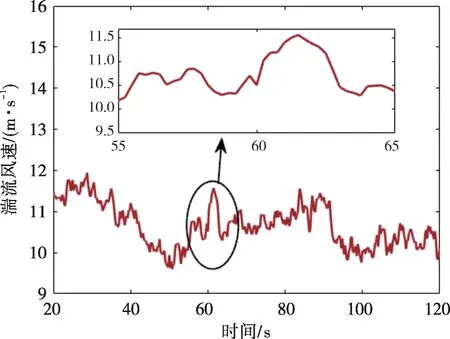
图9 湍流风速曲线
图10 为湍流风下的桨距角对比。其中,当风速增加或减小、控制系统中有前馈控制时,桨距角的变化幅度大于不加前馈控制的桨距角变化幅度。而在DE-模糊PID 控制下,桨距角的变化幅度要大于模糊PID控制下的桨距角。
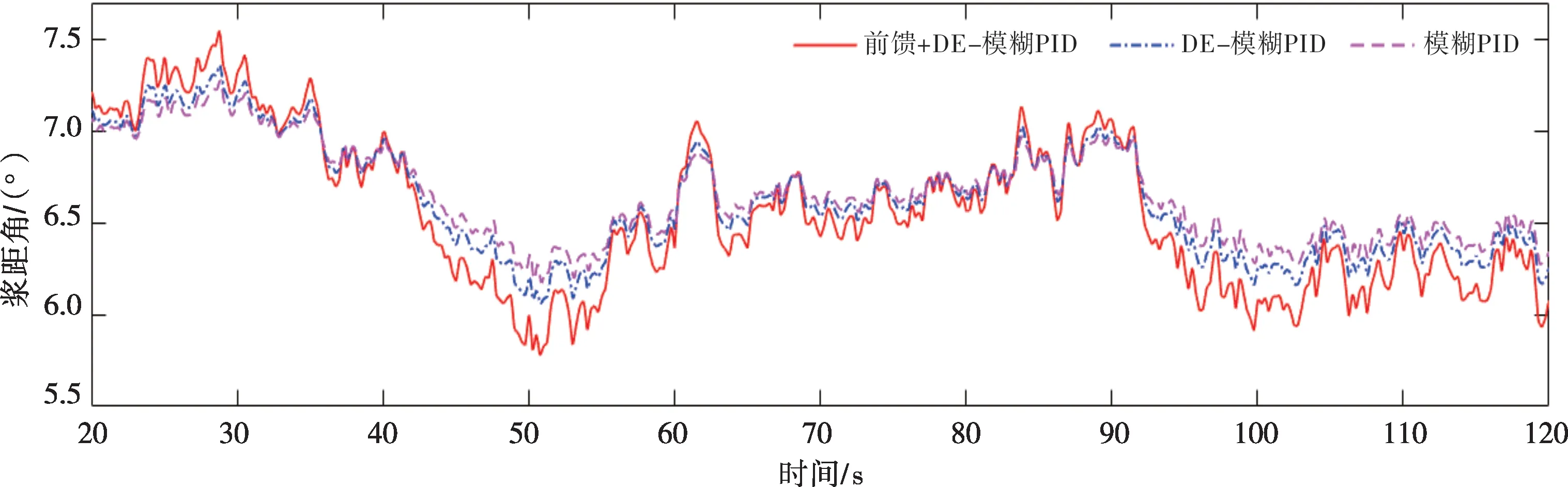
图10 湍流风下的桨距角对比
图11和图12分别为湍流风下的风轮转速和输出功率对比曲线。在前馈控制的作用下,风轮转速和输出功率的波动幅度均小于另外两种控制策略,并且与额定功率的误差更小;在模糊PID 控制下,经过DE初始参数优化的控制策略波动幅度小于未经初始参数优化的波动幅度;在风速变化最大的62 s 附近处,与模糊PID 相比,DE-模糊PID控制下的转速和功率更接近额定值。
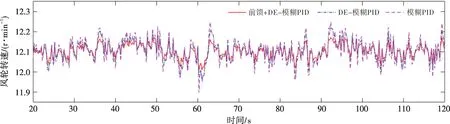
图11 湍流风下的风轮转速对比
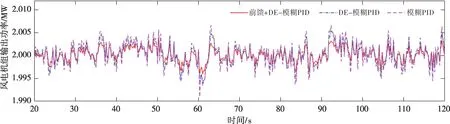
图12 湍流风下的风电机组输出功率对比
3)对系统施加常见的风电机组扰动,扰动包括叶片弯曲形变、安装误差和外部风速变化。在湍流风工况下,对比分析3种控制策略的扰动抑制效果,为便于观察,监测55~65 s风速变化最大时的系统响应,湍流风速如图9所示。
图13—15分别为风电机组施加安装误差扰动、叶片弯曲扰动和风速变化扰动时风电机组的桨距角、风轮转速和输出功率对比曲线。从图13—15可以看出,本文所提控制策略可以有效抑制常见扰动,且该控制策略可使风电机组输出功率更平稳。相较于模糊PID 控制,在DE-模糊PID 控制下风电机组输出功率和风轮转速的波动也略微减小。
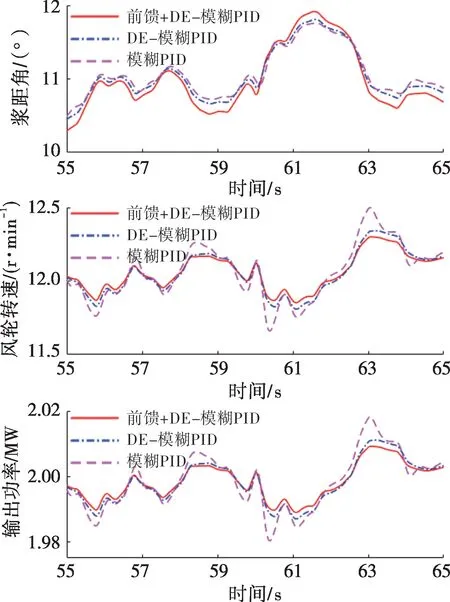
图13 安装误差扰动下的仿真曲线
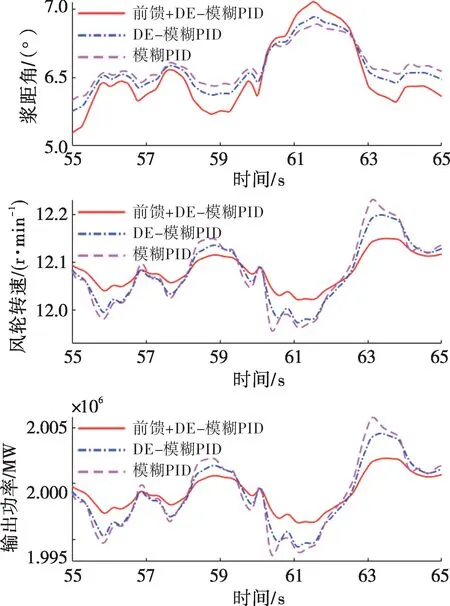
图14 叶片弯曲扰动下的仿真曲线
6 结论
本文针对风电机组变桨控制系统,提出了DE-模糊PID 控制的变桨复合控制策略,即前馈控制与DE-模糊PID 相结合的控制策略。在湍流风、阵风及存在安装误差扰动、叶片弯曲扰动工况下,与DE-模糊PID 控制和模糊PID 控制进行了仿真对比,得出如下结论:
1)在模糊PID控制器的基础上,引入DE算法优化初始参数可使风力的风轮转速和输出功率更平稳,提高了系统的稳定性。
2)将前馈控制与反馈控制结合起来,可以动态补偿风电机组桨距角以弥补反馈控制时滞性,相较于DE-模糊PID 控制和模糊PID 控制,该复合控制策略减小了风轮转速和输出功率的波动幅度。
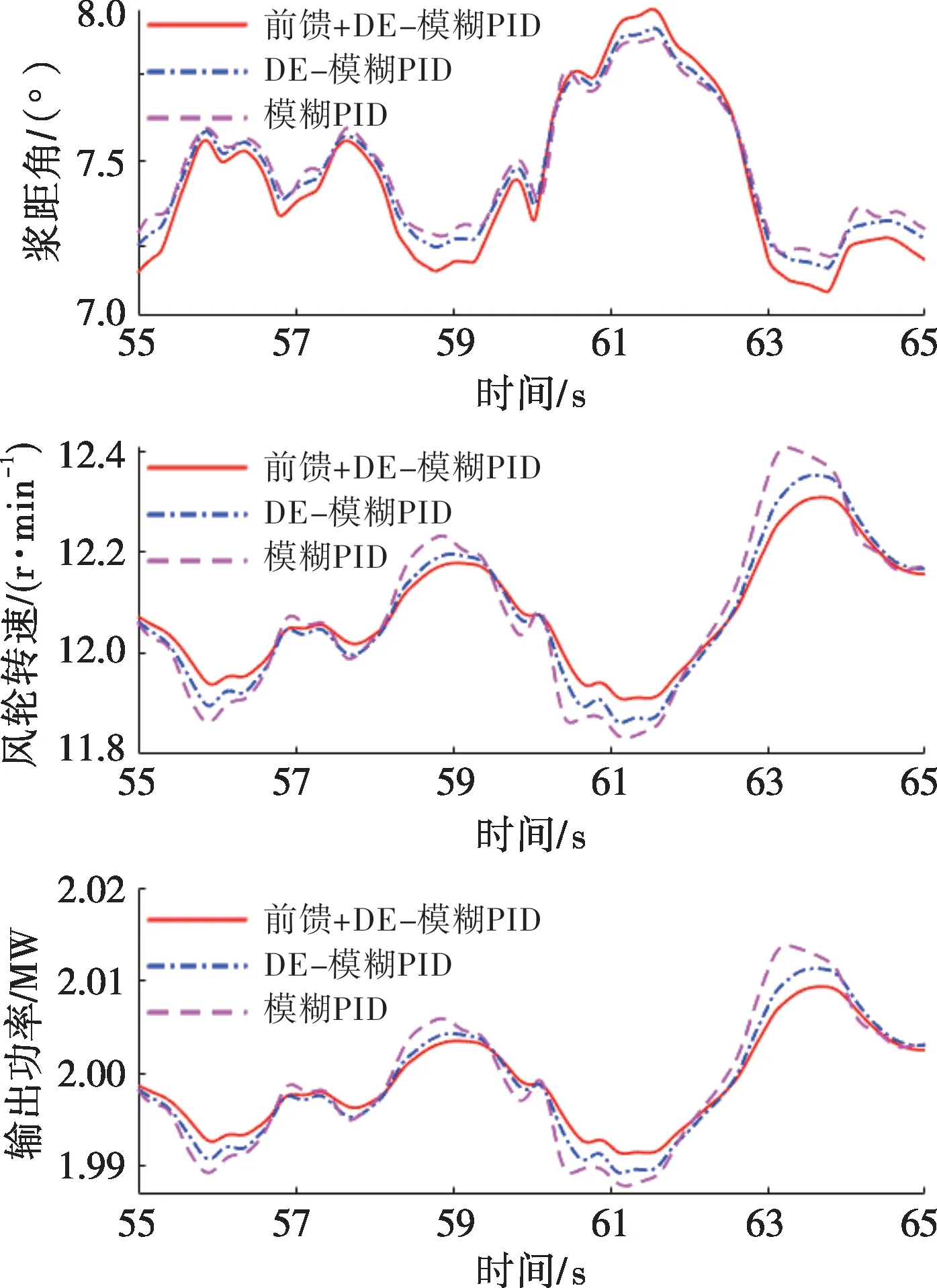
图15 风速变化扰动下的仿真曲线
3)当风电机组受到不同类型的扰动时,前馈+DE-模糊PID 控制均可以起到良好的抑制效果,并且与DE-模糊PID 控制和模糊PID 控制相比,风电机组的风轮转速和输出功率最稳定。
