QM和QDM方法对中国极端气候的高分辨率气候变化模拟的误差订正对比
2022-06-07童尧韩振宇高学杰
童尧 韩振宇 高学杰
1 中国科学院大气物理研究所气候变化研究中心,北京 100029
2 中国科学院大学,北京 100049
3 辽宁省营口市气象局,辽宁营口 110001
4 中国气象局国家气候中心,北京 100081
1 引言
气候模式的模拟结果与观测数据往往存在着一定的系统偏差,若将气候模式结果直接应用于作物模型或者水文模型中,其偏差会对模拟产生很大的影响,因此需要对气候模拟结果进行误差订正(Piani et al., 2010; Yang et al., 2010; Sun et al., 2011)。例如,积温是作物生长发育的重要指标,大部分作物模型中的生育期模型直接与温度或积温相关(Wang et al., 2015)。如果气候模式中温度的模拟存在误差,会对积温产生影响,直接导致作物的生育期延长或缩短,进而影响结实率、灌浆速率等因子,最终影响产量 (Gunarathna et al., 2019)。
常用的误差订正方法是分位数映射方法(Quantile Mapping, QM)(Eden et al., 2012; Maraun, 2013;Ngai et al., 2017)。在建模时段内,计算观测的累计概率分布函数(Cumulative Distribution Function,CDF),并通过构建的传递函数(Transfer Function,TF)使模式数据的CDF与观测尽量接近。发现当基于经验概率分布建立传递函数时(Ashfaq et al.,2010; Teutschbein and Seibert, 2012),尤其是采用非参数转换的方法建立传递函数,不需要对原始数据的概率分布做前提假设,其适应性更广(Boé et al.,2007)。虽然QM方法能够有效地减少模式的偏差,不仅对平均值、年际变化还对极端事件的偏差情况有所改善 (Wood et al., 2004; 童尧等, 2017; 韩振宇等, 2018),但QM可能会人为地改变气候变化信号,如改变模式预估的未来气候趋势(Li et al.,2010; Gudmundsson et al., 2012; Ahmed et al., 2013;Bürger et al., 2013; Switanek et al., 2017)。在气候变化模拟和误差订正研究中,气候变化信号一般是不希望被这种完全基于数学统计关系的误差订正而改变的,因此需要一种能够有效保留预估模拟中未来变化趋势的误差订正方法。目前有越来越多的研究去开发保留趋势的误差订正方法,如delta分位数映射方法(Quantile Delta Mapping, QDM)(Cannon et al., 2015; Tong et al., 2020)、等距累计分布函数方法(EquiDistant Cumulative Distribution Function,EDCDF)(Li et al., 2010)、等比累积概率分布函数匹配方法(equiratio CDF)(Wang and Chen, 2014a, 2014b)、分位数变化方法(delta change, DC)(Olsson et al.,2009)等,这些方法能够基本不改变预估模拟中CDF在未来的相对或绝对变化。
此前已有研究针对区域气候模式模拟的气温和降水的平均态和极端指数,评估了QM方法的订正效果(童尧等, 2017; 韩振宇等, 2018),并对比分析了QM和QDM方法对平均气温和降水模拟值的订正效果(Tong et al., 2020)。在气候变化研究领域,ETCCDI(Expert Team on Climate Change Detection and Indices)极端气候指数(Zhang et al.,2011)被广泛地用以表征极端气候事件。本文旨在利用QM方法和QDM方法对气温和降水的ETCCDI极端指数的订正效果进行分析比较,以便更好地将误差订正方法应用于气候变化模拟预估等研究上。
2 数据与方法
2.1 数据
本文采用的气候变化模拟结果来自区域气候模式RegCM4.4,是意大利国际理论物理中心(the Abdus Salam International Center for Theoretic Physics,ICTP)研发的RegCM4系列中的v4.4版本(Giorgi et al., 2012)。模拟区域为联合区域气候降尺度协同试验东亚第二阶段(CORDEX Phase II East Asia)的推荐区域,覆盖整个中国及其周边的东亚地区。模式的水平分辨率为25 km,模式垂直方向是18层,层顶高度为10 hPa。韩振宇等(2015)更新了中国土地覆盖数据,其他具体的参数设置参见 Gao et al.(2016, 2017)。RegCM4所需的初始和侧边界条件,来自全球气候模式CSIRO-Mk3-6-0(Rotstayn et al., 2010)、EC-EARTH (Hazeleger et al., 2010)、HadGEM2-ES(Collins et al., 2011)、MPI-ESM-MR (Stevens et al., 2012; Jungclaus et al.,2013)和 NorESM1-M (Iversen et al., 2013; Bentsen et al., 2013)。本文用到的模拟数据,包括了历史时段(1981~2005年)以及在RCP4.5情景下(Moss et al., 2010)未来的时段(2006~2098年)(Gao et al., 2018)。5个全球模式驱动下的RegCM4模拟分别简写成CdR、EdR、HdR、MdR和NdR,模式的集合平均用ensR表示。
首先分别对模式输出的日最高气温、日最低气温和日降水数据进行误差订正,然后对模式结果和订正结果分别计算气候极端指数。本文研究内容所选择的ETCCDI极端指数有日最高气温极大值(TXx)、日最低气温极小值(TNn)、连续干旱日数(CDD)和最大日降水量(RX1day)。其中CDD定义为每年日降水量小于1 mm的最大连续日数,RX1day定义为每年最大的日降水量。
用于检验模式结果以及订正效果的观测资料是格点化观测数据集CN05.1,其水平分辨率为0.25°(纬度)×0.25°(经度)。该数据集是基于2400余个中国地面气象台站观测,通过“距平逼近”方法插值建立的,时间是1961~2015年 (吴佳和高学杰, 2013)。CN05.1数据集是基于CN05(Xu et al., 2009) 对700余个中国站点资料进行插值制成的数据集基础上建立发展起来的。由于受站点观测资料的限制,数据集不包括香港、澳门特别行政区及台湾地区。
2.2 误差订正方法
本文选择的QM方法是基于非参数的鲁棒经验分布(Non-parametric quantile mapping using robust empirical quantiles, RQUANT)建立传递函数(Gudmundsson et al., 2012)。该方法是假设经验累积分布函数(CDF)不随时间的变化而变化,具体计算方法和订正原理详见童尧等(2017)。选择的QDM方法 (Cannon et al., 2015)是保留了分位数的变化,即CDF在未来时段的分布发生了变化。其订正原理是,对应每一个分位数,先做一个去趋势的处理,之后再将建模时期构造的传递函数通过QM方法对模式的模拟结果进行订正,最后再将模式的趋势预估值叠加回订正结果中。由于这种相对或绝对变化在误差订正计算中一直被保留,因此QDM订正方法在减小模拟偏差的同时,也可以较好地保留原始模拟结果中的气候变化信号 (Cannon et al., 2015; Tong et al., 2020)。基于同一套观测数据CN05.1,分别采用QM和QDM两种订正方法,对5组RegCM4模拟结果进行订正。订正结果的集合平均,相应地记为ensR_QM和ensR_QDM。
本文的分析主要分为两部分,分别是订正方法的历史时段验证以及未来预估模拟的订正对比分析。在订正方法验证时,受观测资料和模拟数据的时段限制,将1981~2000年(共20年)作为建模期,2001~2015年(共15年)作为检验订正效果的验证时期。Reiter et al.(2016)的研究指出,建模期的长度与订正效果有关,通常长度缩短,订正效果就会降低;因此在实际应用于未来气候变化模拟订正时,会选择尽可能长的历史时段作为建模期。本文在未来预估模拟的误差订正时,选择1981~2015年共35年作为建模期,订正并分析了未来到21世纪末特别是21世纪末期(2079~2098年)相对于1986~2005年气候参照期的变化,讨论订正方法对未来气候变化信号的影响。
2.3 分析方法
本文选择空间相关系数(COR)和均方根误差(Root-Mean-Square Error, RMSE)来衡量数据之间的空间相关性和差异性。在验证时段,用COR和RMSE来检验模式模拟结果以及订正结果与观测之间的偏差情况;在未来预估时段,用两个指标来判断订正结果的未来变化与原始模式结果的未来变化之间的差异和空间相关性,以此来判断是否较好地保留了模式的气候变化信号。另外使用泰勒图(Taylor, 2001)和泰勒评分S(Peng et al., 2020)来定量表现各个模式的模拟性能以及两种误差订正方法对极端指数的订正效果。在计算模拟偏差和未来变化时,RX1day的用相对偏差和相对变化的百分比表征,其他指数的则用绝对变化。
3 结果
3.1 订正结果
3.1.1 温度指数
图1给出了验证时段中国地区TXx和TNn多模式集合平均的模拟偏差以及使用QM和QDM两种方法订正后的结果与观测的偏差。可以看出,模式模拟的TXx在我国大部分地区是偏多的,尤其在西北地区,其偏差在2°C以上;而在内蒙古中东部、青藏高原东南部地区存在较明显的冷偏差,且5个模式模拟的结果较为一致(图1a)。经过误差订正后,偏差在中国大部分地区都集中在±1°C以内;且两种订正方法的误差空间分布相似,都是在我国的中部和东部地区有一定冷偏差,东北地区和青藏高原东部有一定暖偏差(图1b、1c)。
模式模拟的TNn偏差明显大于TXx(图1d),尤其在青藏高原地区偏差值超过了-10°C。模式模拟的冬季气温在青藏高原往往呈现明显的冷偏差(韩振宇等, 2018),年极端最低气温常出现在冬季,因此造成该地区TNn偏差较大。在高纬度地区,除一些山脉附近地区外(如长白山脉、天山山脉和太行山脉等),都为明显的暖偏差。经过QM方法订正后(图1e),其偏差在我国大部分地区都减少到±1°C以内。QDM订正后也能有效地减少模式模拟的偏差情况(图1f),但在中部和南部地区偏差较QM方法大,误差在-5~-2°C之间。在观测中,相较建模时段,验证时段的TNn在内蒙古和新疆等地有一定程度减小而其余地区增加;模式未能较好地模拟这种变化的空间分布,对QDM订正结果产生影响,因而造成QDM在验证时段的订正效果略差(图略)。误差订正对模拟结果中气候变化信号的影响将在后面的3.2节中详细讨论。
表1给出了相对于观测的TXx和TNn,模式模拟结果和两种订正结果在中国范围的RMSE和COR。同时计算了ensR、QM和QDM三者之间的差异显著性以及它们与观测之间的差异显著性,并用显著差异的格点占全国百分比来表征(表1)。ensR模拟的 TXx要好于 TNn,RMSE分别为1.76°C和 7.32°C,经过 QM和 QDM订正后,使RMSE都减少到1°C以下。ensR与观测数据的差异在我国大部分地区都通过了95%显著性检验,而QM和QDM与观测的差异在我国有较少地区通过显著性检验。对于气温极端指数的订正,QDM方法对TXx的订正结果与观测之间的RMSE较小,为 0.59°C,QM 的为 0.62°C;而对于 TNn,则是QM的RMSE较小,为0.79°C,QDM的值为0.92°C。两种误差订正方法都能够有效地减小TXx和TNn与观测结果之间的RMSE。ensR模拟TXx、TNn的空间分布型与观测十分接近,与观测的空间相关系数分别是0.98和0.91,全部通过了95%信度的检验;经过误差订正后,与观测的COR都接近1.00。ensR分别与QM和QDM之间的差异在我国半数格点以上都通过了95%显著性检验,而QM和QDM方法之间则几乎很少地区通过检验,说明两种方法的误差订正效果是显著的,同时两种方法的订正效果无显著差异。
3.1.2 降水指数
模式集合平均对于CDD的模拟(图2a),在准格尔盆地和吐鲁番盆地有极大的正偏差,偏差值大于50 d,在塔里木盆地和我国东南地区也有一定程度的正偏差;此外在中国大部分地区模拟的CDD都是偏少的,尤其在青藏高原和内蒙古地区,负偏差达到了35 d,这是由于模式模拟的冬季降水系统性偏多,造成CDD模拟偏短(童尧等,2017)。模式集合平均结果与观测的RMSE为39.11 d,相关系数为0.46(表1)。经过误差订正后(图2b、2c),有效地减小了模式模拟的偏差,其结果在我国大部分地区的偏差都在±15 d以内,且5个模式偏差的正负一致性较好。两种方法使其订正结果与观测的RMSE分别减小到8.66 d和9.53 d;空间相关系数也都得到了提高,都达到了0.97(表1)。
对于RX1day的模拟结果(图2d),除在西北的盆地地区以及我国的东南地区有一定程度的偏少外,模式的集合平均结果在我国的整个西部和北部地区模拟的都是明显偏多的,尤其在喜马拉雅山脉和横断山脉交界处,其偏差值超过了250%,这可能是受到RegCM系列模式对这些区域降水模拟整体偏多的影响 (Gao and Giorgi, 2017; Gao et al.,2017),也与格点观测资料在站点稀疏地区的不确定性有关 (吴佳和高学杰, 2013)。经过QM和QDM的订正后(图2e、2f),其偏差在我国的大部分地区都集中在±25%之间,其中QM方法的订正结果相对较好(图2e)。通过表1的数值可以更清楚看出误差的订正效果,订正后将ensR与观测的RMSE(23.30%)分别减少到6.88%(QM)和7.92%(QDM),空间相关系数也从0.77分别提高到了0.98和0.97。对于降水极端指数的订正,两种订正方法的效果无明显差别,只是QM方法的全国平均RMSE较小一些。有关降水指数模拟误差和订正效果的显著性检验结果与温度指数类似(表1),其中COR也均通过了95%显著性检验。

图2 同图1,但为连续干旱日数(CDD)和最大日降水量(RX1day)Fig.2 Same as Fig.1, but for the Consecutive Dry Day (CDD) and Max 1-d precipitation amount (RX1day)

表1 验证期(2001~2015年)模式集合平均(ensemble RCM, ensR)和订正结果(QM和QDM)与观测之间的均方根误差(RMSE)和空间相关系数(COR),ensR、QM和QDM三者之间及与观测之间的显著差异的格点占全国百分比Table 1 Root-mean-square error (RMSE) and spatial correlation coefficient (COR) between the simulation of ensemble RCM (ensR) and bias corrections and the observation during the verification period (2001-2015), as well as the percentage of grid points with significant differences among the observation, ensR, QM, and QDM over China
从给出的5种区域气候模式集合平均结果的泰勒图(图3a)能够看出,模式对于气温指数的模拟效果要好于降水,其中对TXx模拟的偏差最小且空间相关系数最高。经过误差订正后,使各指数的偏差都明显减小,空间相关系数也得到了有效的提高,所有指数的COR都达到0.97以上,对气温指数的订正结果相对于降水指数更加靠近观测值(REF),相关系数接近1.00。图中还能看出,两种误差订正方法的订正效果无明显差异。

图3 验证期(2001~2015年)误差订正前后模式在中国地区的模拟性能:(a)泰勒图;(b)空间相关系数;(c)S评分Fig.3 Skills of simulations and bias correction in the extreme climate indices over China during the verification period (2001-2015): (a)
3.1.3 不同模式的模拟性能及其订正效果
基于5组模拟结果及其QM和QDM方法订正后结果,分别计算极端气候指数,并进行误差的定量评估(图3b和3c)。在模式模拟的极端气候指数中,对TXx模拟的空间相关系数最高(都超过0.95),其中HdR的COR值最大。相对而言,TNn模拟值与观测的COR(0.8~0.95)都低于TXx的,RX1day模拟值的COR相对更低(0.6~0.9),也是HdR的模拟效果较好。CDD模拟值与观测的COR相对最小;其中EdR的COR值最高,也仅为0.5左右;MdR模拟的最差,与观测的COR在0.30以下。经过误差订正后,无论是QM方法还是QDM方法,都对不同模式不同极端指数与观测的COR得到了有效地提高,尤其是对TXx和TNn,在5个模式和集合平均结果中其COR都达到了0.99;对于降水指数CDD的订正结果COR提升到了0.95以上;RX1day的订正结果则是除CdR模式外,其余与观测的COR也都达到了0.95以上(图3b)。
在泰勒评分S图(图3c)中,也能更清楚地看出,模式对于降水指数的模拟技能较差,尤其是CDD,其中对CDD的模拟中CdR和MdR模式评分在5个模式和集合平均中较低,在RX1day的模拟中CdR和NdR的评分较低。经过误差订正后,对于气温极端指数TXx和TNn,无论是哪种订正方法,在各个模式中评分都达到了1.98以上;降水极端指数的订正结果评分虽然较温度低,但评分整体都有了大幅度的提高了。总体来说,QM和QDM方法都能够针对不同的模式结果进行订正,使订正后的结果与观测更为接近。
3.2 未来变化
3.2.1 气温指数
图4给出了中国地区模式集合平均及其订正结果在21世纪末(2079~2098年)的极端气温指数变化,预估TXx和TNn未来在整个中国地区都是显著增加的。多模式集合平均模拟TXx的未来变化值多在2.1~3.0°C之间,全国平均值为2.45°C(图4a)。经过QDM订正后(图4c),其结果在大小和空间分布上都显示与ensR非常接近,全国平均增加2.58°C;而在ensR_QM中则发现较大的差异(图4b),除西北的盆地地区增温幅度较ensR小外,在我国大部分地区的增温都较大,造成了在中国地区平均增温值也变大,为2.67°C。通过表2也能进一步量化说明,ensR_QM与ensR的变化之间的RMSE为0.59°C,相关系数为0.34,而ensR_QDM与模式的结果更为接近,RMSE为0.20°C,相关系数达到 0.80。

图4 21世纪末(2079~2098年)的TXx(左列)和TNn(右列)变化(相对于1986~2005年):(a、d)ensR;(b、e)ensR_QM;(c,f)ensR_QDM。图中左下角给出了整个中国的区域平均值且整个中国区域全部通过了95%显著性检验Fig.4 Projected changes in TXx (left panel) and TNn (right panel) at the end of the 21st century (2079-2098 in relation to 1986-2005): (a, d) ensR;(b, e) ensR_QM; (c, f) ensR_QDM.The regional mean over the entire China is provided in the lower-left corner of the panels.All the changes over China are statistically significant at the 95% confidence level
相对于TXx,ensR预估的TNn未来变化幅度更大,增幅多在2.4~4.0°C之间(图4d)。从TNn的模拟结果与订正结果未来变化分布图来看,ensR_QDM很好地保持了ensR的原始信号,ensR_QM则没有(图4e、4f)。模式集合平均对TNn未来预估的全国平均值是增加3.20°C(图4d),经过QM订正后的TNn未来变化结果是整体偏小的(图4e),全国平均值仅为2.20°C,与订正前模式预估值的RMSE为1.21°C,空间相关系数仅为0.55,偏差较大(表2);而ensR_QDM无论从空间分布情况还是变化幅度上都较QM结果与模式原始模拟的未来变化都更为接近(图4f),全国平均增加2.95°C,与订正前模式预估值的RMSE为0.34°C,相关系数达到了0.96(表2)。表2给出了ensR、QM和QDM预估结果三者之间的差异显著性。其中,QM与QDM方法之间的显著差异的格点占全国百分比,TXx和TNn分别达到了46%和56%;而QDM与ensR的未来变化结果更为接近(显著差异比例仅为11%和3%),可以说明,在对未来气候变化信号的保留中,QDM方法较优。
总而言之,QM方法明显改变了原始模式的TXx和TNn变化信号,而QDM方法可以很好地保留它。
3.2.2 降水指数
图5是ensR、ensR_QM和ensR_QDM的降水指数CDD和RX1day 在21世纪末的变化。ensR模拟的未来CDD在高纬度地区是减少的,而在低纬度地区是呈现增加的趋势,减少的大值区在塔里木盆地、柴达木盆地和内蒙古高原西部,因此造成全国平均的CDD变化为负值,即-1.87 d(图5a)。经过误差订正后,无论是ensR_QM还是ensR_QDM都能够再现CDD的未来变化是高纬度减少低纬度增加,但减少幅度较ensR大,尤其是QM方法,其全国平均变化值为-5.22 d,而ensR_QDM的平均变化值为-3.87 d,与ensR更为接近(图5b、5c)。从统计指标来看,ensR_QM与ensR变化之间的RMSE为 6.07 d,相关系数为 0.56;ensR_QDM与ensR变化间的RMSE为4.00 d,相关系数为0.66;因此QDM方法的预估结果更接近ensR。
对RX1day的ensR模拟中,在我国大部分地区未来变化是增加的,且无明显的区域差异,全国平均变化幅度为12.32%(图5d)。QM方法误差订正能一定程度地保留ensR模拟的RX1day的气候变化信号,但在喜马拉雅山脉和昆仑山脉等区域的未来变化增加更为明显,达到35%以上,全国平均变化为 16.08%(图5e)。而 QDM能较比QM方法在数值和分布上更接近ensR的情况,但也有一定程度上偏多趋势,全国平均的未来变化为14.50%(图5f)。表2的统计分析显示,QDM和QM在保留RX1day的气候变化信号上RMSE都较小,空间相关系数较高;但相比而言,QDM方法的预估结果更接近ensR,ensR_QM和ensR_QDM与ensR的RMSE分别为8.51%和6.37%,相关系数分别为0.68和0.75。对于CDD和Rx1day的未来变化,QM与QDM之间的存在显著差异的格点比例较小,但以ensR表征的未来变化为基准,QM与其显著差异的格点比例仍略高于QDM的。因此全国平均变幅、RMSE、COR和差异显著性等多个方面的评价都显示,对于降水极端事件的气候变化信号保留,仍是QDM方法较好。
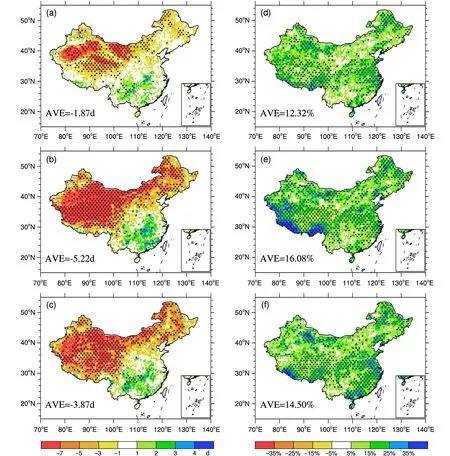
图5 同图4,但为CDD和RX1day。打点区域表示为通过95%显著性检验Fig.5 Same as Fig.4, but for the CDD and RX1day.The dot area indicates that they are all statistically significant at the 95% confidence level

表2 21世纪末(2079~2098年)极端指数变化(相对于1986~2005年)在订正结果QM和QDM与未订正模拟结果ensR中的RMSE和COR以及ensR、QM和QDM三者之间显著差异(95%信度)的格点占全国百分比Table 2 RMSEs and CORs of the changes (2079-2098 in relation to 1986-2005) in the extreme indices between the QM/QDM and ensR, as well as the percentage of grid points with significant differences (95%) among the ensR, QM, and QDM over China
3.2.3 未来变化的时间序列
图6给出的是1981~2098年中国地区极端指数相对于1986~2005年平均的距平时间序列,从图中能够看出全国平均的4个极端指数在1981~2098年间都表现出明显的线性变化趋势和年际及年代际变化特征。对于气温指数,整体呈现明显的线性增加(图6a、6b)。在TXx中,QM和QDM订正结果的变化与ensR的变化基本一致,全国平均序列的变化趋势也接近(图6a)。表3给出的是ensR和QM以及QDM在全国平均序列的变化趋势值(均通过了95%显著性检验)和两种订正方法与ensR之间的RMSE。ensR模拟的变化趋势是0.27°C/10 a(表3),ensR_QM 的结果为 0.30°C/10 a,与 ensR的 RMSE为 0.17°C;而 QDM的结果与ensR更为接近,为0.28°C/10 a,RMSE也减少到0.12°C。对于TNn来说(图6b),其变化曲线波动振幅较大,年际变化更为明显。在2040年以后,ensR_QM的增幅与ensR相差较大,整个时段的RMSE为0.65°C(表3),而 ensR_QDM的变化特征与ensR更为接近,RMSE为0.27°C(表3)。ensR模拟TNn变化的趋势是0.36°C/10 a,ensR_QM预估的变化趋势较小,为0.25°C/10 a,而ensR_QDM的结果与ensR更为接近,为0.33°C/10 a(表3)。因此对于气温极端指数的全国平均变化序列的订正,QDM方法较好。

表3 全国平均时间序列的变化趋势及订正结果QM和QDM与未订正模拟结果ensR的RMSETable 3 Linear trends in future changes in the regional mean over the entire China and the RMSE between the QM/QDM and ensR

图6 极端指数变化的时间序列:(a)TXx;(b)TNn;(c)CDD;(d)RX1dayFig.6 Time series of extreme index changes: (a) TXx; (b) TNn; (c) CDD; (d) RX1day
CDD则表现更为明显的年际和年代际变化特征,且呈现减小的线性趋势(图6c),ensR预估的全国平均序列变化趋势为-0.22 d/10 a(表3)。ensR_QM和ensR_QDM在2040年之后的变化都较ensR的变化有明显偏低的情况(图6c),因此两种订正方法的变化趋势值偏低,分别为-0.59 d/10 a和-0.43 d/10 a(表3)。其中QDM方法的偏差较小,RMSE为1.40 d,而 QM方法相应的RMSE为 2.25 d(表3)。对RX1day的变化序列图中能看出(图6d),其变化有明显线性增加趋势,ensR的线性趋势值为1.36%/10 a(表3),在2020年之后ensR_QM和ensR_QDM的变化较ensR是偏多的,且ensR_QM的偏差较大(图6d)。通过表3更能清楚地说明这一现象,ensR_QM和ensR_QDM的变化趋势分别为1.74%/10 a和1.57%/10 a,且QDM与模式的RMSE更小,为2.77%(QM为3.15%)。在降水极端指数的全国平均变化序列的订正中,仍然是QDM方法较好。
4 结论和讨论
本文主要是基于5个全球模式驱动下RegCM4.4模式的气候变化模拟结果,采用QM和QDM两种误差订正方法对模拟的气温和降水数据进行订正,然后分别计算模式结果和订正结果的极端气候指数并进行了对比分析。气温的极端气候指数选取了TXx和 TNn,降水的极端指数选取了CDD和RX1day。首先介绍了模式对4个极端气候指数的模拟偏差,并对两种订正方法进行评估,包括针对多模式集合和各个模式的订正对比;然后分析误差订正方法对气候变化信号的影响,包括未来变化幅度、变化的空间分布以及全国平均值的距平时间序列等。
历史时期ensR的偏差情况与其他GCM和再分析数据驱动的模式结果具有一致性(Tong et al.,2020; Wu and Gao, 2020)。气温指数中对TNn的偏差更大,尤其在青藏高原地区有明显的冷偏差。而对降水指数的模拟中,对CDD除了在准格尔盆地和吐鲁番盆地有极大的正偏差,以及我国东南地区的正偏差外,在我国大部分地区的模拟结果都是偏小的,而对RX1day的模拟在我国北方大部分地区是偏多的,这可能也与RegCM系列模式对我国北方降水模拟整体偏多有关。对于不同模式,气温指数的模拟效果普遍较好,而降水指数的模拟效果相对较差,尤其是对CDD的模拟。QM和QDM两种订正方法都可以有效地减少这些误差,使得订正后的模拟结果与观测更为接近,降低RMSE的同时也很大程度的提高了与观测的空间相关系数;并且两种方法的订正结果差异较小,无明显优劣之分。这一结论对于多模式集合和各个单独的模拟结果都是适用的。
对于气温极端指数未来变化的结果中,QM方法改变了模式原始模拟值预估的TXx和TNn变化信号,而QDM方法可以很好地保留它,ensR_QDM无论在变化幅度还是变化的空间分布上都十分接近ensR。对于降水极端指数的未来变化中,两种方法在一定程度上都保留了气候变化信号,但对未来CDD在我国北方减少和RX1day大范围增加的变化幅度有一定高估,相较而言仍然是QDM方法的保留效果较好。
在极端指数的未来变化序列图中能够看出,4种指数,除了CDD是呈减小的线性趋势外,都是表现明显的线性增加,并且有年际和年代际的特征。在TXx中,两种方法与ensR的变化都比较接近;对于TNn和CDD,在2040年之后,QM与QDM的波动变化与ensR的偏离明显,其中QM方法偏差更大;在RX1day中,在2020年之后偏差就比较明显,也是QM方法偏差更大。变化趋势的定量比较以及相较ensR的RMSE分析显示,QDM方法与ensR的变化更为接近。
综上可以得出,QDM方法在对气候变化模拟误差订正中的优势更为突出,不仅能减少模拟偏差,也能有效保留极端指数在未来的气候变化信号,使时间序列的变化趋势也与模式原始预估值接近。值得注意的是,误差订正方法并不能提高模式本身的模拟和预估技巧。模拟技巧的提高依赖于模式的改进和输入数据的精度提高等,预估技巧的提高在模式改进的基础上还依赖于对气候系统内部变率的深入理解和未来社会经济情景的合理设定,QDM方法正是保证了在误差订正的同时不引入额外的预估不确定性。QDM方法可广泛用于其他的全球和区域气候模式,但其订正效果及与QM方法的对比还有待评估;同时,未来工作中将进一步改进订正效果的检验方法,如采用交叉验证方法等。
