逆极限以及双重逆极限空间中利普希次跟踪性和几乎周期点的研究
2022-06-07冀占江陈占和张更容
冀占江,陈占和 ,张更容
(1.梧州学院 大数据与软件工程学院,广西 梧州 543002;2.梧州学院 广西高校行业软件技术重点实验室,广西 梧州 543002;3.梧州学院 广西高校图像处理与智能信息系统重点实验室,广西 梧州 543002;4.广西大学 数学与信息科学学院,广西 南宁 5430004;5.湖南第一师范学院 数学与计算科学学院,湖南 长沙 410205)
0 引言
逆极限空间是动力系统研究的一个分支,它为构造复杂空间和映射提供了有力的工具,跟踪性在动力系统中占有重要的地位,与计算机和生物数学的发展有着密切的关系,很多学者对逆极限空间和跟踪性的动力学性质进行了深入的研究,得到有价值的研究成果[1-11]。例如,文献[1]指出若每个映射fi具有逐点伪轨跟踪性,则其诱导映射f∞具有逐点伪轨跟踪性;文献[2]证明了自映射f具有渐近伪轨跟踪性当且仅当移位映射σ具有渐近伪轨跟踪性;文献[3]证明了若每个映射fi具有遍历跟踪性,则其诱导映射f∞具有遍历跟踪性;文献[4]证明了f具有平均跟踪性当且仅当对任意的q∈[0,1),f具有平均跟踪性。 然而以上文献中并未涉及逆极限空间中利普希次跟踪性的动力学结果,为了完善逆极限空间的理论,本文在逆极限空间中研究了自映射f与移位映射σ在利普希次跟踪性方面的关系,得到移位映射σ具有利普希次跟踪性当且仅当自映射f具有利普希次跟踪性。
随着研究的深入,当我们研究复杂问题时,会发现逆极限空间的有限个符号已经难以解决生活中遇到的实际问题,而双重逆极限空间是极限空间的推广,因此研究双重逆极限空间[12-15]就成了一项有意义的工作。但是目前有关双重逆极限空间的文献并不多,理论也有待学者进一步探讨和研究,本文根据逆极限空间中几乎周期点的概念,提出双重逆极限空间中新几乎周期点的概念,然后在双重逆极限空间中研究了它的拓扑结构和拓扑特征,得到移位映射的几乎周期点集等于自映射在其几乎周期点集上形成的双重逆极限空间,从而丰富了双重逆极限空间中的理论成果,为双重逆极限空间在实际中的应用提供了理论依据。
1 基本定义
定义1 设X,Y是拓扑空间,称f是一个同胚映射,如果f:X→Y是一个一一映射,并且f和f-1都是连续的。
定义2 设(X,d)是紧致度量空间,且f:X→X是连续映射。若令

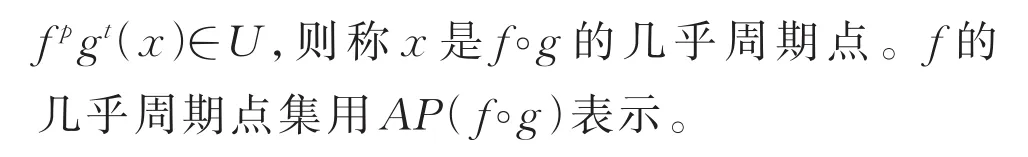
定义6 设 (X,d)是度量空间,f:X→X 连续。 若存在常数L>0与δ>0,对任意的0<ε<δ,使 得 当是 f的 ε-伪 轨 ,∃x∈X,xLε-跟踪{xi}∞i=0,则称f具有利普希茨跟踪性。
定义7[16]设(X,d)是度量空间,f:X→X 连续。若存在L>0,对任意的x和 y∈X有d(f(x),f(y))≤Ld(x,y),则称 f是利普希茨映射,L为f的利普希茨常数。
2 引理
引理 1[15]设 (X,d)是 紧 致 度 量 空 间 ,f:X→X,g:X→X 同 胚 映 射 ,f◦g=g◦f,则∀i,j∈Z,∀m,n≥0,有 πi,jσfnσgm=fngmπi,j。
3 主要定理
定理1 设(X,d)是紧致度量空间,Xf是X的逆极限空间,f:X→X 连续满射,σ:Xf→Xf是移位映射。若f是常数为L的利普希映射,则f具有利普希茨跟踪性当且仅当σ具有利普希茨跟踪性。

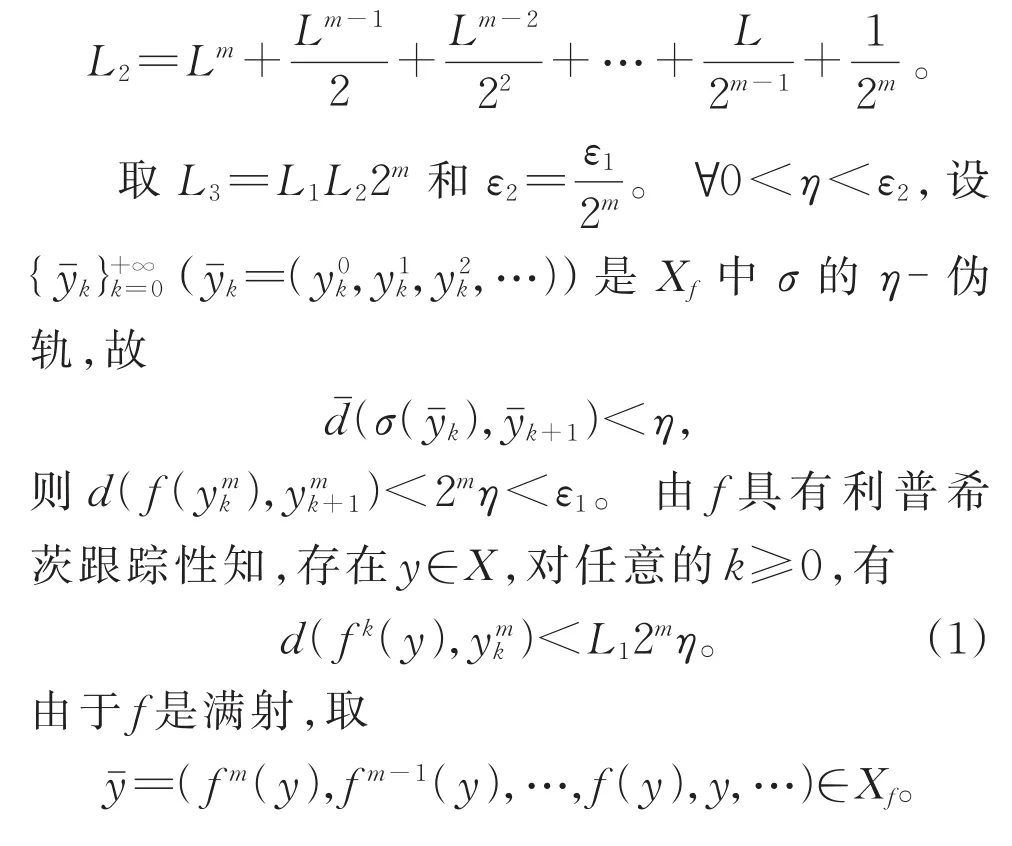

4 结论
本文在逆极限空间中研究了利普希茨跟踪性的等价性,然后在双重逆极限空间中研究了几乎周期点集的拓扑结构,所得结果推广了逆极限空间中跟踪性和几乎周期点的结论。
