线性矩阵方程AXB+CXD=F的斜埃尔米特迭代解

杨 吉, 黄光鑫, 尹 凤

(1.成都理工大学 数学地质四川省重点实验室，成都 610059； 2.成都理工大学 数理学院,成都 610059；3.成都理工大学 计算机与网络安全学院(牛津布鲁克斯学院),成都 610059)

针对线性矩阵方程组

AXB+CXD=F

(1)

的斜埃尔米特矩阵解的求取，提出了2个基于梯度的松弛算法，其中矩阵A、C∈r×n，B、D∈n×s和F∈r×s是已知的，而X∈Sn×n是未知的。

线性矩阵方程(1)在应用数学和控制理论的一些领域中发挥着重要作用[1]。Sylvester矩阵方程在线性系统理论中有很多应用，如极点特征结构配置[2]、鲁棒极点配置[3]、观测器设计[4]、模型匹配问题[5]、广义系统的正则化[6]、干扰解耦问题[7]和非交互控制[8]。Ding F.等[9]提出了一种求解矩阵方程AXB=F与Sylvester矩阵方程组(1)的迭代方法；Yuan S.F.等[10]讨论了分裂四元数矩阵方程(1)的埃尔米特解；Yuan S.F.等[11]利用四元数矩阵的复杂表示，推导了四元数矩阵方程组(1)的2种特殊的最小二乘解：Moore-Penrose广义逆和矩阵的克罗内克积。

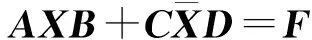
1 迭代算法

首先研究方程(1)有斜埃尔米特解的充要条件。在此基础上，提出了求解方程(1)的斜埃尔米特解的改进的梯度迭代算法。

引理1[1]矩阵方程(1)有唯一的斜埃尔米特解XS∈Sn×n的充分必要条件是矩阵方程组

(2)

有唯一的解，且通解X*∈n×n和

根据引理1，我们构造一种改进的梯度迭代算法来求解矩阵方程(1)的斜埃尔米特解。对于复矩阵方程AXB=F，有如下基于梯度的迭代算法[9,15]。

引理2对于复矩阵方程AXB=F，如果A是列满秩矩阵，B是行满秩矩阵，则基于梯度的迭代算法生成的迭代解X(k)，对于任意初始矩阵X(0)

X(k+1)=X(k)+μAH(F-AX(k)B)BH

(3)

收敛于精确解X*(limk→∞X(k)=X*)，当且仅当

(4)

记扩展后的矩阵方程(1)为以下2个线性矩阵方程形式

AXB=F-CXD，CXD=F-AXB

(5)

Ding F.等[9]提出了下面这个算法求解矩阵方程组(1)。

X1(k)=X(k-1)+μAT{F-AX(k-1)B
-CX(k-1)D}BT

(6)

X2(k) =X(k-1)+μCT{F-AX(k-1)B
-CX(k-1)D}DT

(7)

这里X(k)是X1(k)和X2(k)的平均值，即

(8)

据文献[9]，只要μ满足

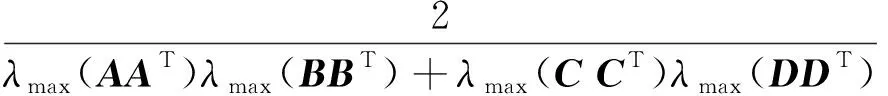
(9)

则(6)式和(7)式所表示的梯度迭代算法收敛。利用算法(6)式和(7)式的思想，可以得到求解矩阵方程(1)的斜埃尔米特解的改进迭代算法。

算法1求解矩阵方程(1)斜埃尔米特解的梯度迭代算法。

步骤1： 给定任意2个初始近似解块向量X1(0)，X2(0)，并且X(0)=(X1(0)+X2(0))/2。

步骤2： 对于k=1,2,…,n， 直到收敛。

步骤3：X1(k)=X(k-1)+μ[AH{F-AX(k-1)B-CX(k-1)D}BH+CH{F-AX(k-1)B-CX(k-1)D}DH]。

步骤4：X2(k)=X(k-1)+μ[B{-FH-BHX(k-1)AH-DHX(k-1)CH}A+D{-FH-BHX(k-1)AH-DHX(k-1)CH}C]。

步骤5：X(k)=(X1(k)+X2(k))/2。

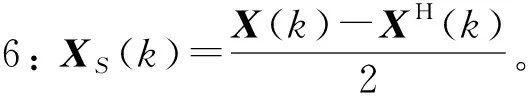
步骤7： 结束。

定理1如果矩阵方程(1)是相容的并且有唯一解X*，那么只要μ满足

(10)

则由算法1生成的迭代序列X(k)就收敛到X*，即对于任意初始值X(0)，limk→∞X(k)=X*或X(k)-X*收敛到0(零矩阵)。进一步地，序列{XS(k)}收敛XS，这里XS是矩阵方程(1)的唯一斜埃尔米特解。

证明将估计误差矩阵定义为

(11)

对于k=1,2,…,n, 并且

(12)

利用上述误差矩阵(11)和(12)以及算法1和矩阵方程(1)，很容易得到

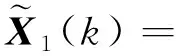
-CX(k-1)D}DH]

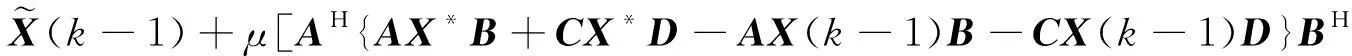
+CH{AX*B+CX*D-AX(k-1)B-CX(k-1)D}DH]

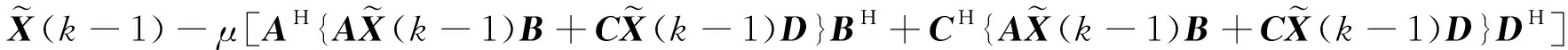
(13)

与(13)式类似，可以得到

(14)

取(13)式和(14)式两边的Frobenius范数，就得到下面结果

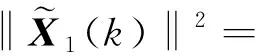
-η(k-1)}BH‖2+‖CH{-θ(k-1)-η(k-1)}DH‖2]

+ηH(k-1){-θ(k-1)-η(k-1)}]+μ2[‖AH{-θ(k-1)-η(k-1)}BH‖2

+‖CH{-θ(k-1)-η(k-1)}DH‖2]

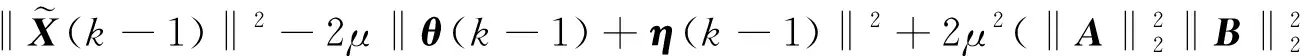
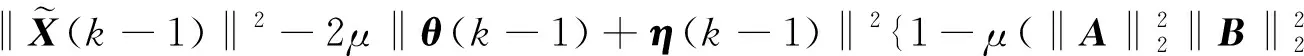
类似地，有

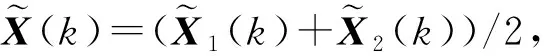
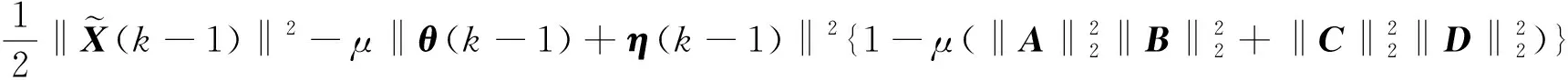
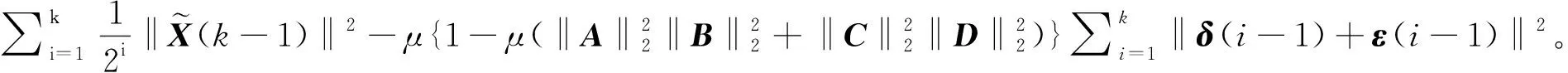
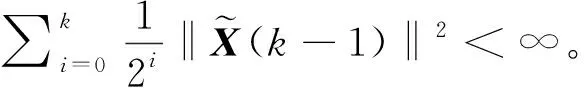
那么有

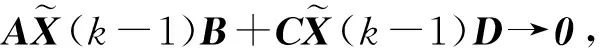
证毕。

算法2求解矩阵方程(1)斜埃尔米特解的改进梯度迭代算法(MGI)。

步骤1： 给定任意2个初始近似解块向量X1(0)，X2(0)，并且X(0)=(X1(0)+X2(0))/2。

步骤2： 对于k=1,2,…,n, 直到收敛。

步骤3：X1(k)=X(k-1)+μ[AH{F-AX(k-1)B-CX(k-1)D}BH+CH{F-AX(k-1)B-CX(k-1)D}DH]。

步骤4：X(k-1)=[X1(k-1)+X2(k-1)]/2。

步骤5：X2(k)=X(k-1)+μ[B{-FH-BHX(k-1)AH-DHX(k-1)CH}A+D{-FH-BHX(k-1)AH-DHX(k-1)CH}C]。

步骤6：X(k)=[X1(k)+X2(k)]/2。

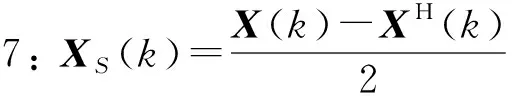
步骤8： 结束。

下面给出算法2的收敛性。

定理2如果矩阵方程(1)是相容的并且有唯一解X*；那么只要(满足

(15)

则由算法2生成的迭代序列X(k)就收敛到X*，即对于任意初始值X(0)，limk→∞X(k)=X*或X(k)-X*收敛到0。进一步地，序列{XS(k)}收敛到XS，这里XS是矩阵方程(1)的唯一斜埃尔米特解。

证明将估计误差矩阵定义为

(16)

对于k=1,2,…,n,有

(17)

利用上述误差矩阵(16)和(17)以及算法2和矩阵方程(1)，很容易得到

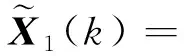
-CX(k-1)D}DH]

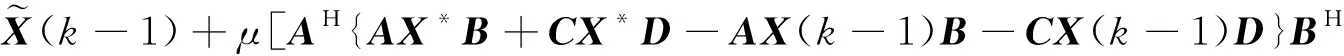
+CH{AX*B+CX*D-AX(k-1)B-CX(k-1)D}DH]

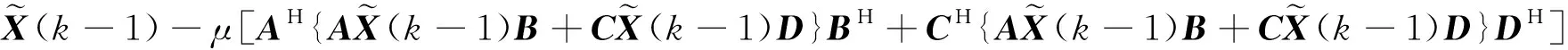
(18)

类似地，有

(19)

取(18)式和(19)式两边的Frobenius范数，则

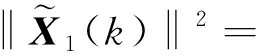
-η(k-1)}BH‖2+‖CH{-θ(k-1)-η(k-1)}DH‖2]

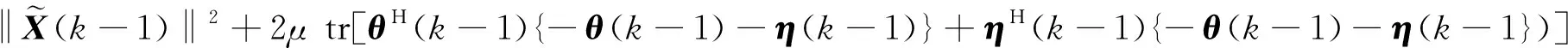
+μ2{‖AH(-θ(k-1)-η(k-1))BH‖2+‖CH(-θ(k-1)-η(k-1))DH‖2}

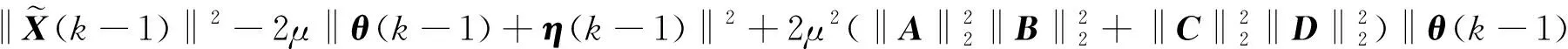
+η(k-1)‖2

类似地，有

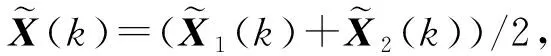
那么有

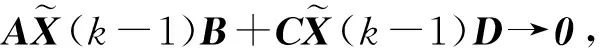
证毕。

2 数值实例

给出2个数值实例用于说明算法1和算法2。所有的测试都使用MATLAB R2014a实现。

例1算法1和算法2求矩阵方程(1)的斜埃尔米特迭代解，其中

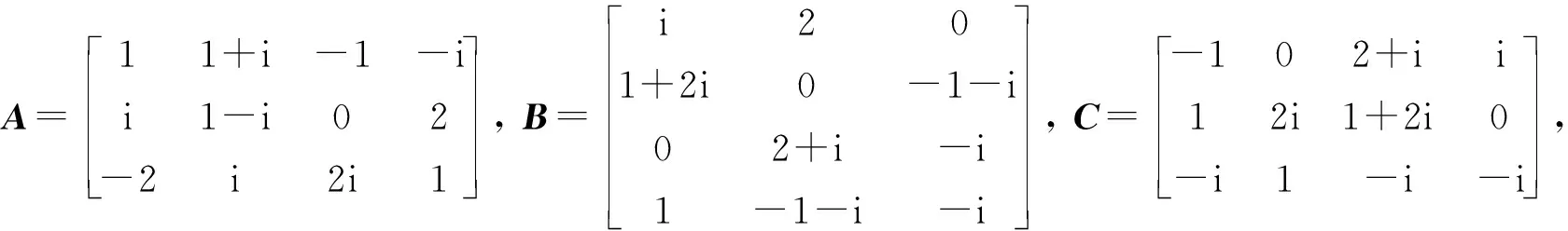
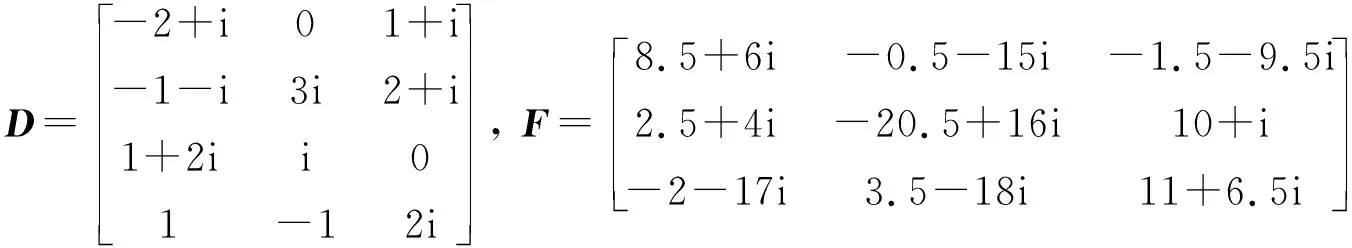
初始矩阵选择为

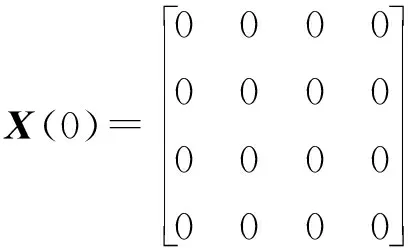
容易验证，该矩阵方程(1)具有唯一的斜埃尔米特解

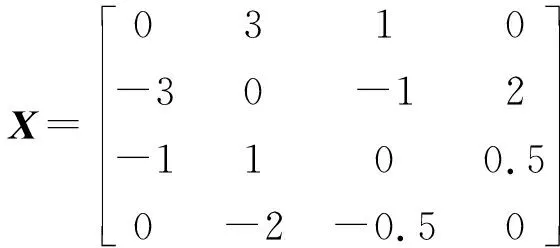
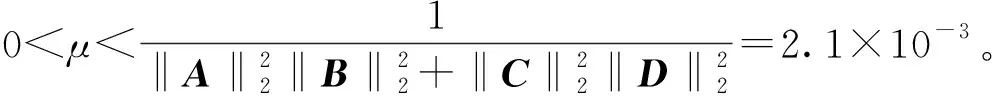
例2考虑大型矩阵方程(1)的斜埃尔米特迭代解，其中

A=round(rand(20,20)*2)-1-i*round(rand(20,20)*5)-1;

C=round(rand(20,20)*2)-1-i*round(rand(20,20)*5)-1;

B=round(rand(20,20)*2)-1-i*round(rand(20,20)*5)-1;

D=round(rand(20,20)*2)-1-i*round(rand(20,20)*5)-1。

式中：rand(m,n)生成m×n阶均匀分布的随机矩阵；rand(k)表示对数k四舍五入取整；i为虚数单位。

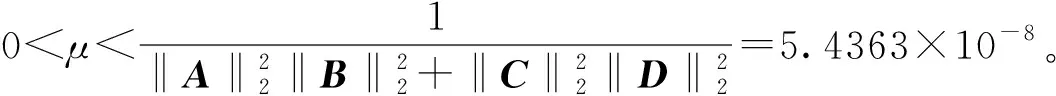
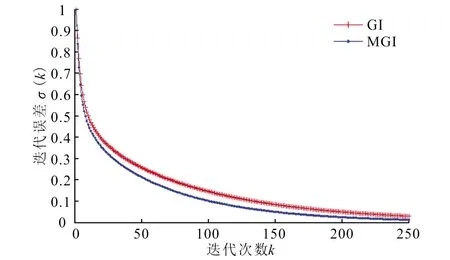
图1 GI算法和MGI算法的收敛性能Fig.1 Convergence performance of GI algorithm and MGI algorithm

图2 GI算法和MGI算法的收敛性能Fig.2 Convergence performance of GI algorithm and MGI algorithm

3 总 结

本文提出了2种求解线性矩阵方程AXB+CXD=F的斜埃尔米特解的梯度形松弛迭代算法，即梯度迭代(GI)算法和改进的梯度迭代(MGI)算法，并分析了算法的收敛性，数值实例说明了算法的有效性。