层状软岩隧道非对称大变形控制解耦方法

韦 猛, 林 宇

(地质灾害防治与地质环境保护国家重点实验室(成都理工大学)，成都 610059)

中国西部山区的地质构造极其复杂，区域内广泛分布着层状变质软岩。随着隧道建设在该区域大规模展开，层状软岩各向异性特征[1]导致的隧道非对称大变形现象大量出现，如汶马高速鹧鸪山隧道[2]、成兰铁路茂县隧道[3]等。因此，层状软岩隧道开挖稳定性控制是山区隧道建设面临的重大挑战。

国内外学者对层状软岩隧道形变控制措施开展了大量的研究。沙鹏等[4]通过兰渝铁路两水隧道的现场试验，得到了深埋层状岩体的挤压形变特征，并提出了对应的形变控制措施；徐国文等[5]以汶马高速鹧鸪山隧道为依托，对两台阶与三台阶开挖条件下千枚岩地层隧道的形变特征及支护结构受力特性进行了研究，结果表明，两台阶开挖围岩来压快，洞周变形值及围岩与初期支护压力值相对偏大，钢拱架安全储备相对不足；曲懋轩[6]基于对倾斜薄层状围岩巷道失稳机理的统计分析，提出了通过施作长短锚杆相结合的支护方式来控制围岩大变形；任耀文[7]分析了陡倾小交角层状岩体隧道的典型失稳特征，提出以优化锚杆长度和角度为核心的非对称支护方法；李磊等[8]基于成兰铁路杨家坪隧道，对高地应力陡倾互层千枚岩地层隧道大变形特性进行了研究，提出了针对非对称大变形的优化断面轮廓、注重围岩加固、控制锚杆角度、减少开挖分部、增加支护刚度的形变控制措施；吴迪等[9]以蓝家岩隧道为例，对高地应力深埋层状围岩隧道非对称变形受力机制进行了研究，提出在最不利位置施作压力型锚索或局部加强支护来解决围岩的非对称大变形问题；郭健等[10]基于现场实测，对炭质板岩隧道围岩非对称大变形与衬砌受力特征进行了研究，提出合理地释放围岩应力是有效控制隧道非对称大变形的关键；张俊儒等[11]针对层状围岩的非对称变形特征，对高地应力陡倾板岩隧道的合理洞型选择展开了研究，得到了单线隧道最优高跨比。

通过上述分析发现，目前对于层状岩体隧道大变形控制的研究，较少对岩体大变形的复合机制进行针对性的研究，也就鲜有对基于非对称复合大变形机制的形变控制措施的研究。因此，针对目前研究的不足，本文首先建立能考虑锚杆拉伸断裂及钢支撑压弯破坏的数值计算模型，然后以汶马高速鹧鸪山隧道为对象开展现场测试，并对层状软岩隧道非对称大变形控制解耦方法进行研究。通过采用非对称支护与优化开挖方法，将岩体的复合形变力学机制转换成单一形变力学机制，然后再进行针对性的支护控制。研究结果可以对层状软岩隧道大变形控制的设计与施工提供一定的指导。

1 数值方法

1.1 支护体系的建立

1.1.1 锚杆断裂力学模型

锚杆是一种重要的维持围岩稳定的主动支护方式；但实际工程中，大变形条件下锚杆断裂的案例较为普遍。以深部巷道为例，其锚杆破断失效的情况非常严重，部分回采巷道的锚杆破断率高达65%以上(图1-A)[12]。因此，在数值计算中，需要考虑到锚杆的断裂失效，否则会夸大锚杆的支护能力。

李为腾等[12]提出了锚杆拉伸断裂的模拟方法，本文在其研究基础上，通过FLAC3D内置fish语言编程，实现了锚杆拉伸断裂的模拟。FLAC3D中，锚杆杆体单元为典型的理想弹塑性单元，其杆体结构的内力-位移曲线关系如图1-B所示，内力-位移关系的表达式为

(1)

图1 锚杆力学行为Fig.1 Mechanical behavior of rock bolt

式中：u为锚杆杆体的拉伸或者压缩位移；Ft为锚杆杆体单元的抗拉强度；Fc为锚杆杆体单元的抗压强度；k为锚杆杆体单元的轴向拉压刚度。

当锚杆的形变值超过其极限形变值时，锚杆杆体会产生断裂，断裂处锚杆的轴力变为0，锚杆对围岩的支护作用就会有极大程度的减弱。因此，引入锚杆的拉断准则对锚杆断裂行为进行描述[9]

F=0， (u(i)≥umax)

(2)

式中：u(i)为锚杆任一单元的长度；umax为该单元所对应的极限长度。

因此，考虑杆体断裂的锚杆轴向本构关系为

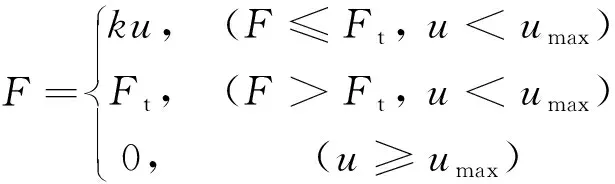
(3)

1.1.2 钢拱架断裂力学模型

对于软弱地层而言，钢拱架支护容易进入塑性变形阶段，甚至产生扭曲变形、接头张开等大变形现象[13](图2)。因此，在数值计算时，需要考虑钢拱架的塑性力学行为。FLAC3D自带的beam单元，其轴力随着应变的增大而线性增长，无屈服阶段；其弯矩随着弯曲应变的增加体现出理想弹塑性特征。可见，beam单元的力学行为不能反映钢拱架的塑性特性。

因此，本文在模拟时引入钢拱架截面的广义屈服条件[14]。

当n≤Aw/A(即中性轴位于腹板内)时

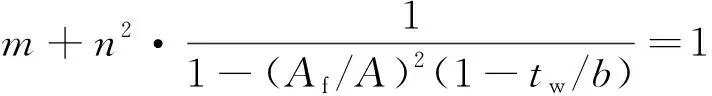
(4)

当n>Aw/A(即中性轴位于翼缘内)时

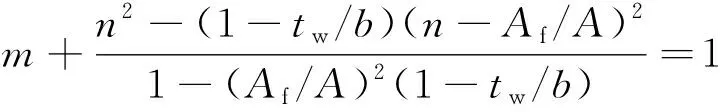
(5)

式中：A、Af、Aw分别为工字钢的截面总面积、翼缘板面积与腹板面积；tw、b分别为工字钢的腹板宽度、翼缘宽度；n、m为构件内力的无量纲系数。

图2 钢拱架大变形Fig.2 Large deformation of steel arch(据周艺[13])

n=N/Nu

(6)

m=M/Mu

(7)

式中：N、M分别为钢架的实际轴力、弯矩；Nu、Mu分别为钢架轴力、弯矩的极限值。

1.1.3 超前注浆小导管

本文数值模型中，不建立超前注浆小导管，而是将小导管的加固作用通过提高围岩的参数来实现，具等效方法为[15]：

等效加固圈的容重在围岩与浆液容重之间取值，计算公式为

γsg=mγg+(1-m)γs

(8)

式中：γs、γg分别为围岩、浆液的容重；γsg为等效加固圈的容重。

小导管对围岩参数的影响可按下式计算

(9)

式中：φs、cs、Es分别为围岩的内摩擦角、黏聚力和弹性模量；φsg、csg、Esg分别为等效加固圈的内摩擦角、黏聚力和弹性模量；Rt为导管的抗拉强度设计值；A为导管的截面积；e、i分别为导管群的纵向、横向间距。

1.2 层状岩体各向异性力学模型

采用FLAC3D中的遍布节理模型[16]对层状岩体的各向异性特征进行描述。其中，对于岩石基质体，服从图3-A所示的Mohr-Colulomb准则

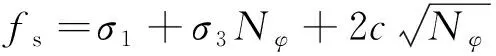
(10)

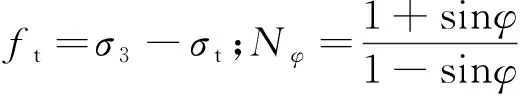
(11)

式中：fs为剪切破坏准则；ft为拉伸破坏准则；c、φ、σt分别为岩石的黏聚力、内摩擦角及抗拉强度。

对于软弱面，破坏准则为

fs=τ+σ3tanφj-cj(拉伸)

(12)

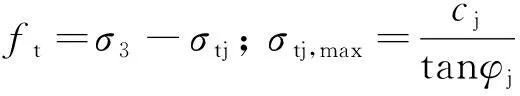
(13)

式中：cj、φj、σtj分别为节理的黏聚力、内摩擦角及抗拉强度。

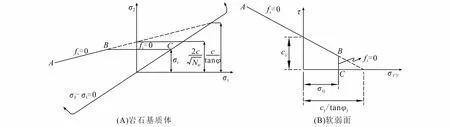
图3 遍布节理模型Fig.3 Ubiquitous Joint model

2 数值模型的建立

2.1 工程概况

鹧鸪山隧道左线长 8 808 m，右线长 8 778 m，最大埋深 1 392 m。该隧道位于阿坝藏族自治州理县与马尔康市交界处，进口与国道317线相邻，地理位置如图4-A所示。隧道洞身围岩以三叠系新都桥组、侏倭组及杂谷脑组炭质千枚岩和板岩为主(图4-B)，属于软弱岩层，高地应力条件下极易发生大变形，如喷射混凝土开裂、隧道轴线两侧非对称变形以及钢拱架扭曲以及二次衬砌开裂等(图5)。

为了对层状围岩地层结构的力学行为进行研究，在现场典型断面埋设了土压力盒对围岩压力进行测试。同时，在二次衬砌的主筋上埋设混凝土应变计对二次衬砌的受力进行测试(图6)。可以看出，测试结果体现出较为明显的各向异性特征。具体而言，围岩压力在左拱肩位置最大，该位置开挖轮廓线的切线与层理面方向近于平行。对于二次衬砌而言，正弯矩(向隧道内侧弯曲)在左拱肩与右拱脚出现最大值，而负弯矩(向隧道外侧弯曲)在右拱肩与左拱脚附近出现最大值。截面全环范围内轴力均为正值，最大值位于右拱肩与左拱脚附近。可见，对于层状岩体而言，开挖轮廓线的切线与层理面方向近似平行的截面承担最大的围岩压力，最大的正弯矩及较小的轴力。因此，该位置为隧道结构安全的薄弱环节。

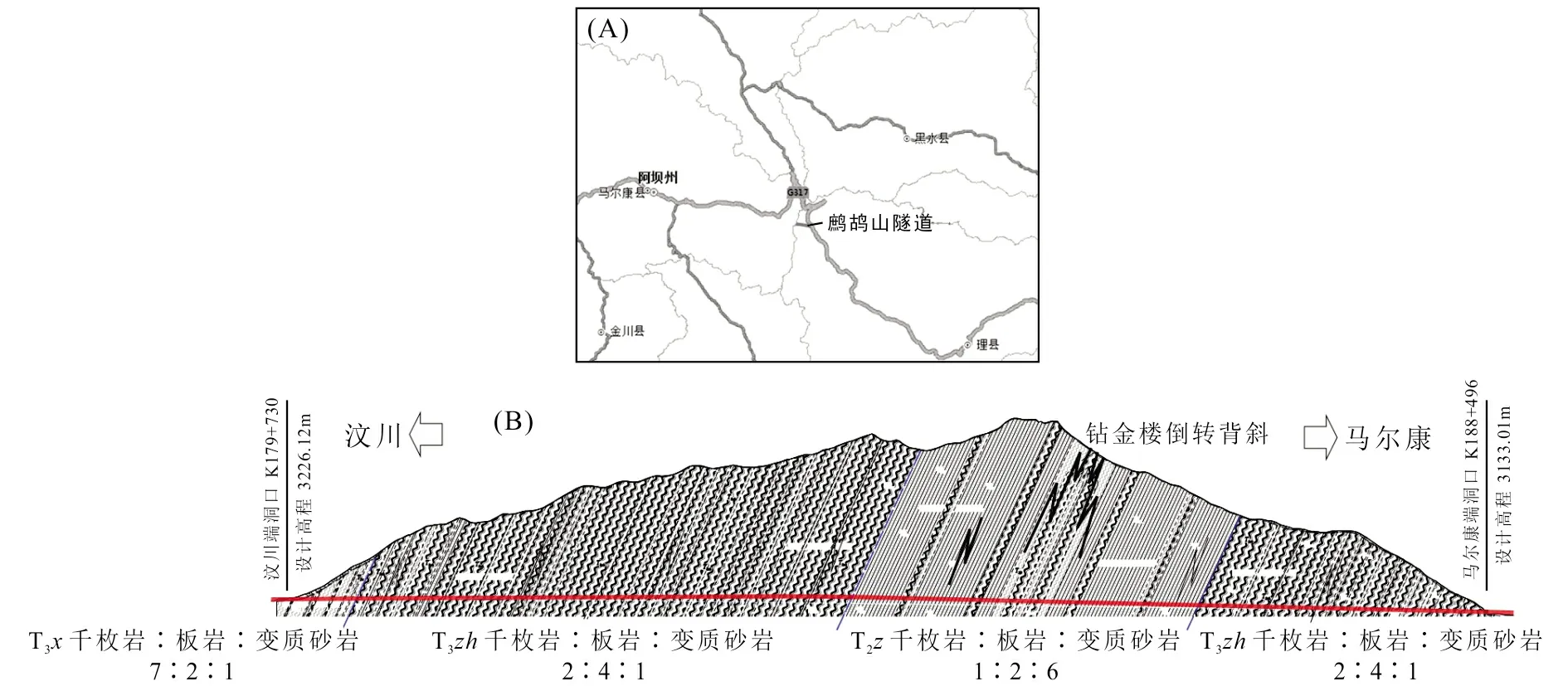
图4 鹧鸪山隧道位置与地质纵断面图Fig.4 Location and profile of the Zhegushan tunnel

图5 鹧鸪山隧道典型围岩大变形特征Fig.5 Typical large deformation in the Zhegushan tunnel

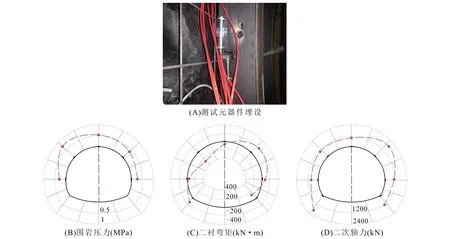
图6 现场测试Fig.6 Site test

2.2 数值模型的建立

以鹧鸪山隧道为对象，采用FLAC3D开展针对性数值模拟，以研究层状软岩隧道大变形控制解耦技术。建立的计算模型如图7所示，为消除边界效应的影响，模型的长度与高度均为40 m，纵向为20 m, 取模型纵向中部截面进行分析。模型的上表面为自由边界，其余5个面约束边界节点的法向位移。锚杆、钢拱架的力学参数如表1、表2所示。喷射混凝土为C20素混凝土，厚度为20 cm，采用满足摩尔库伦准则的实体单元进行模拟，力学参数如表3所示。层状千枚岩的力学参数如表4所示。

图7 数值计算模型Fig.7 Numerical calculation model

表1 锚杆与注浆体力学参数Table 1 Mechanical parameters of rock bolt and grouting

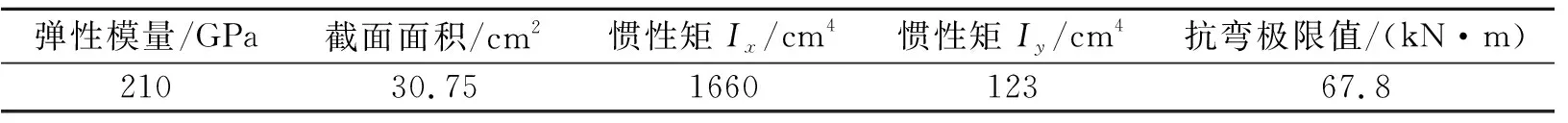
表2 钢拱架力学参数Table 2 Mechanical parameters of steel arch

表3 喷射混凝土力学参数Table 3 Mechanical parameters of shotcrete

表4 层状岩体力学参数Table 4 Mechanical parameters of layered soft rock

根据《汶马高速鹧鸪山隧道高地应力及岩爆、大变形防治研究》[17]，鹧鸪山隧道通过板岩、千枚岩地层。千枚岩单轴抗压强度值为5～12 MPa，本文取千枚岩强度为5 MPa进行研究。根据地应力反演结果，地应力工况为：σx(水平方向主应力)取值为10 MPa、15 MPa或20 MPa；λ(侧压力系数，λ=σy/σx)=0.5、1.0或1.5。具体工况如表5所示(注：计算工况中，岩石的挤压程度根据Hoek提出的挤压因子确定[18]，计算公式为Nc=σcm/p0，式中：σcm为岩体单轴抗压强度，p0为原岩地应力)。当Nc<0.11、 0.11≤Nc<0.16、 0.16≤Nc<0.22、 0.22≤Nc<0.36、Nc≥0.36时，围岩的挤压程度分别为极严重、严重、中等、轻微、不明显。

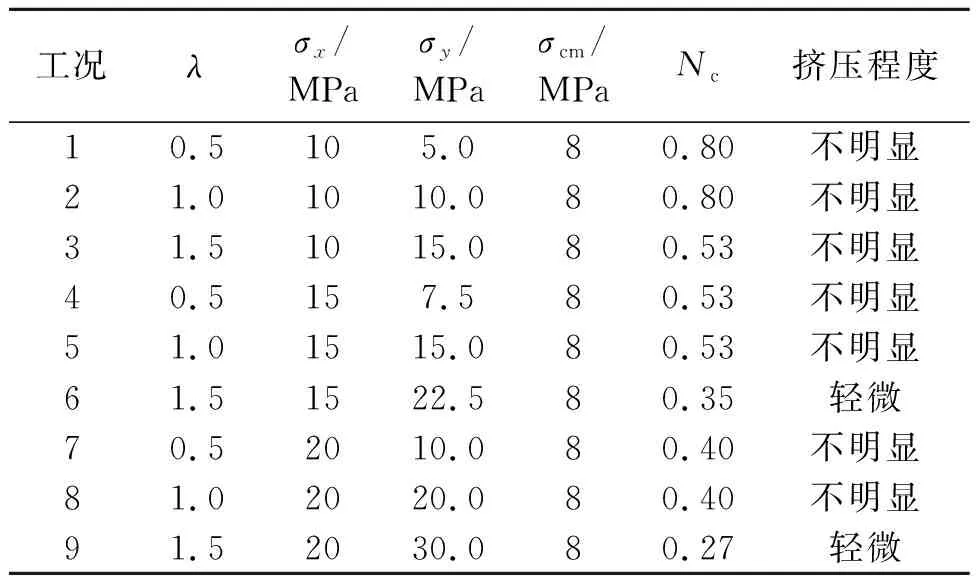
表5 计算工况表Table 5 Studied cases

3 计算结果分析

3.1 两台阶常规支护计算结果

当开挖方式采用两台阶开挖时，台阶长度为2 m；且支护结构中锚杆长度为3 m，纵环向间距为1 m，钢拱架型号为I20，纵向间距为0.6 m；初期支护为C20喷射混凝土，厚度为20 cm；超前小导管注浆支护范围为拱顶周边60°。此时，工况1～工况5支护结构未出现断裂失效，工况6～工况9支护结构均出现断裂失效。

3.1.1 层理面倾角的影响

可以看出，当β=15°时(β为层理面与水平方向的夹角，图7)，围岩塑性区主要分布在左拱肩与右拱脚附近(图8)；当β=45°时，塑性区主要分布在拱顶与拱底附近(图9)；当β=75°时，塑性区主要分布在右拱肩与左拱脚附近(图10)。各种角度下，位移最大值均分布在左右拱腰附近，但较大位移区域中心的连线会随着层理面的方向偏转。从锚杆受力来看，当β=15°、45°和75°时，锚杆受力较大区域分别分布在左拱肩、拱顶与右拱腰区域，且这些区域均为对应各角度下塑性变形显著区域。从钢支撑受力来看，轴力较大位置也与塑性形变显著的区域重合，且全环范围内弯矩均较小。对支护结构的受力分析可以看出，各种工况下初期支护均处于弹性变形阶段，说明对应的支护结构可以较为有效地控制围岩的变形。

图8 层理面倾角对隧道开挖的影响(β=15°)Fig.8 Influence of inclined angle of structure plane on tunnel excavation (β=15°)

图9 层理面倾角对隧道开挖的影响(β=45°)Fig.9 Influence of inclined angle of structure plane on tunnel excavation (β=45°)

图10 层理面倾角对隧道开挖的影响(β=75°)Fig.10 Influence of inclined angle of structure plane on tunnel excavation (β=75°)

3.1.2 支护结构失效行为

以工况9围岩倾角β=45°为例，对支护结构失效行为进行分析，计算结果如图11所示。从图11-A中可以看出，围岩的塑性区主要分布在左右拱腰区域。由图11-B可知，围岩的最大位移分布在右拱腰与左拱脚附近，最大值为327 mm。系统锚杆中，总共有8根锚杆产生了拉断，拉断顺序是：11、3、19、12、10、18、2、1，主要集中在右拱腰与左拱脚(图11-C)。同时，钢拱架轴力分布较大的区域也出现在左拱脚与右拱腰附近，且钢架的部分截面也产生了断裂失效，说明两台阶开挖条件下，对应的常规支护结构不能有效地控制围岩的变形。

图11-F为锚杆断裂过程。从图中可以看出，断裂锚杆的受力经历了3个较为明显的变化阶段：首先，锚杆的轴力波动上升；当锚杆轴力达到其轴力极限值时，锚杆的受力保持不变；最后，当锚杆的拉伸长度达到其极限拉伸长度时，锚杆发生断裂，断裂截面处锚杆的轴力立即变为零。图11-G为钢支撑典型断裂截面的内力变化曲线。从钢支撑轴力变化特性可以看出，钢支撑的轴力先线性增加，当接近其极限轴力值时，轴力量值保持不变；而对钢支撑弯矩而言，随着时间的增加，其量值非线性减小，最终变为零。

从上述分析可以看出，层状岩体隧道中，围岩的变形与支护结构的受力都体现出明显的各向异性特征。隧道开挖后，由于层理面的回弹效应，导致垂直于层理面方向的围岩产生较大的塑性区与塑性变形，进而导致在该部分围岩附近的锚杆与钢拱架发生大变形而失效。

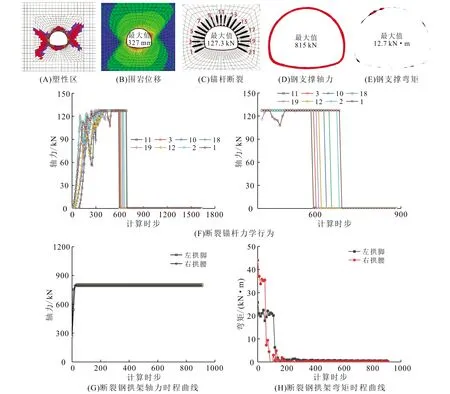
图11 工况9计算结果(β=45°)Fig.11 Numerical calculation results of case 9 (β=45°)

3.2 非对称大变形解耦技术

从上述分析可以看出，对鹧鸪山隧道而言，层理面对围岩大变形特征有较大的影响，因此，结构变形型大变形是隧道大变形的主要类型；同时，由于塑性区的剪切滑移效应，塑性区的扩容也较为明显：因此，其大变形是由结构变形型与应力扩容型共同作用导致。所以，本文提出的大变形复合变形力学机制向单一变形力学机制转化的控制技术如下：①优化施工方法，将应力扩容型与结构变形型复合大变形转化为结构变形型单一大变形；②若仅优化施工方法难以有效地控制大变形，则在此基础上优化支护措施。通过非对称支护手段，对结构变形型单一大变形进行控制。上节数值模拟中，当采用两台阶开挖及常规支护时，工况6～工况9中支护结构均出现了大变形失效，难以对围岩的形变进行有效控制。因此，本节基于上述大变形控制思想，对围岩的大变形进行控制。

3.2.1 优化施工方法

对于工况6而言，将两台阶开挖转换为三台阶开挖，台阶进尺、支护参数与两台阶一致。以β=15°为例，得到的计算结果如图12和图13所示。从图中可以看出，当改变开挖方法以后，围岩的塑性区与位移都有所减小，最大位移值从242 mm减小到203 mm；同时，支护结构都处于弹性状态，锚杆轴力最大值为120 kN，钢拱架轴力最大值为765 kN，弯矩最大值为12 kN·m：说明改变开挖方式后，支护结构能有效控制围岩的变形。因此，对于该工况而言，仅改变开挖方式就可以有效控制围岩的应力扩容型大变形，而常规的支护手段可以控制围岩的结构型大变形。

对工况6当β=45°时在两台阶开挖下的支护措施与开挖措施进行参数分析，得到的结果如表6所示。作为标准对比的支护手段如3.1节所示。在进行参数化分析时，只改变单一参数，其余参数与标准组相同。

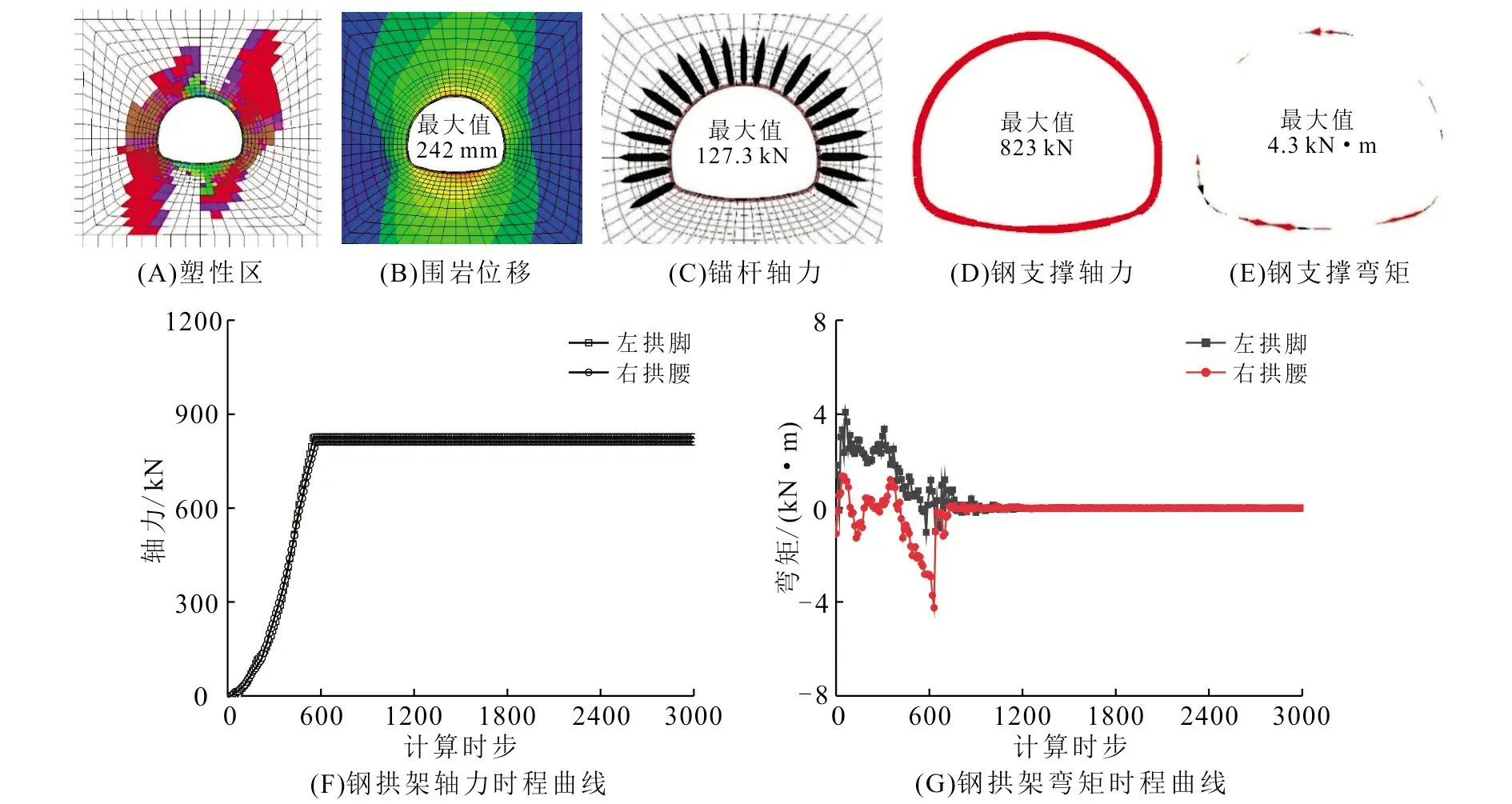
图12 工况6二台阶常规支护计算结果(β=15°)Fig.12 Numerical calculation results of case 6 with two-bench excavation method (β=15°)

图13 工况6三台阶常规支护计算结果(β=15°)Fig.13 Numerical calculation results of case 6 with three-bench excavation method (β=15°)

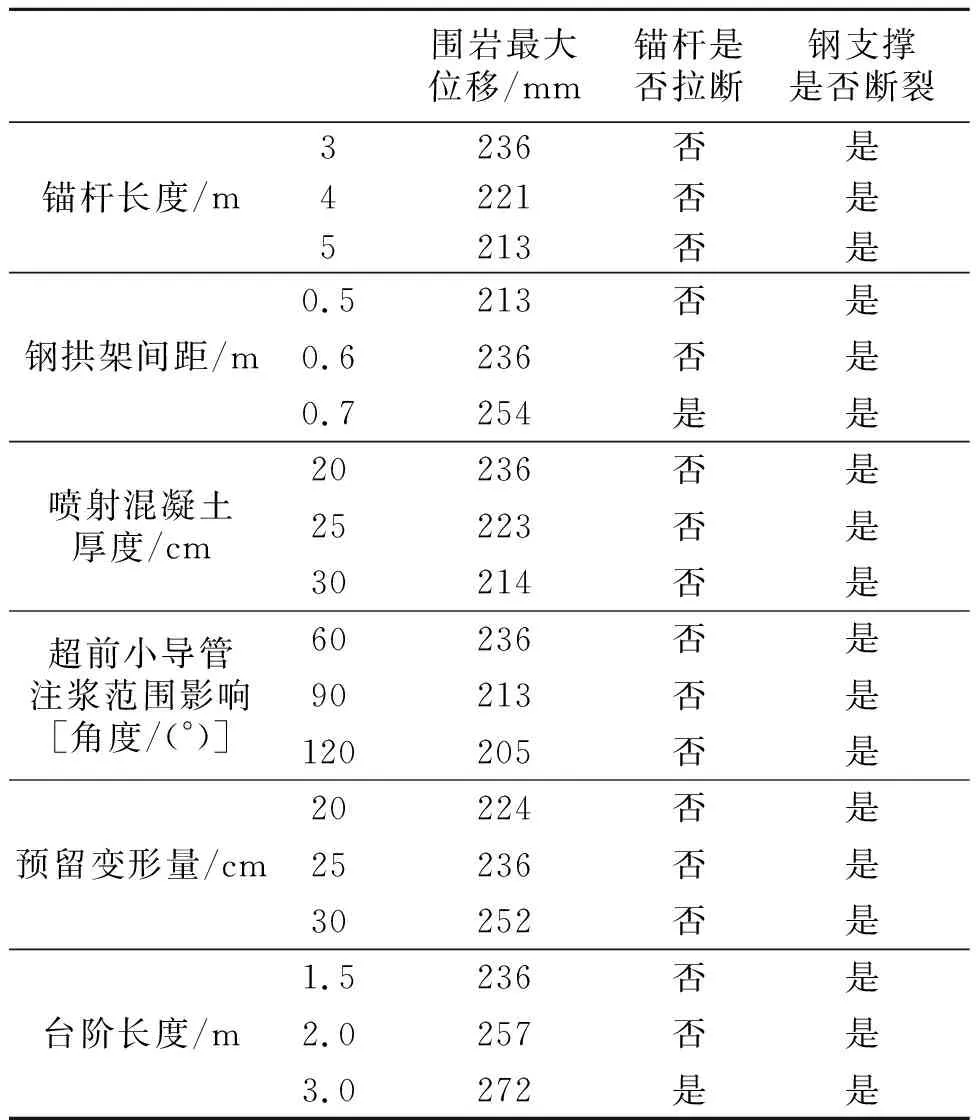
表6 支护与开挖参数影响Table 6 Influence of the mechanical parameters of primary lining and excavation method on tunnel excavation

从表6中可以看出，强化支护结构或减小台阶开挖长度，可以减小围岩的位移；但多数情况下，支护结构依然会产生大变形破坏。因此，在该种工况下，改变开挖方法是较为合理的大变形控制措施。

3.2.2 优化施工方法与支护手段

对于工况9中β=45°而言，首先将两台阶开挖转换为三台阶开挖，台阶进尺不变，得到的计算结果如图14所示。与图9对比可以看出，当改变开挖方法以后，围岩的塑性区与位移都有所减小，最大位移值从327 mm减小到287 mm。系统锚杆中仅拱顶正上方锚杆出现了断裂。同时，钢拱架轴力较大区域分布在左右拱腰，钢拱架也多处出现了断裂。说明相对于工况9(轻微挤压大变形)而言，仅改变开挖方法，难以有效地控制围岩大变形。

因此，在三台阶开挖的基础上，在围岩形变较大的区域设置长锚杆，即采用非对称锚杆支护，计算得到的结果如图15所示。与图11-A对比可以看出，当采用非对称锚杆支护以后，围岩的塑性区域位移都有进一步的减小，最大位移值从287 mm减小到251 mm。系统锚杆与钢支撑均处于弹性受力状态，未产生断裂破坏。

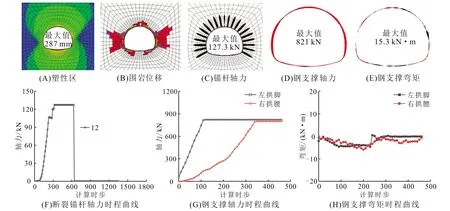
图14 工况9三台阶开挖方法计算结果(β=45°)Fig.14 Numerical calculation results of case 9 with three-bench excavation method (β=45°)

4 结 论

本文以汶马高速鹧鸪山隧道为工程背景，对层状软岩隧道大变形控制的解耦技术进行了研究，得到的主要结论如下：

a.考虑锚杆及钢拱架断裂的数值模型可以较好地反映初期支护在围岩大变形条件下的断裂失效，能更为准确地表征支护结构的实际支护力学行为。

图15 工况9三台阶开挖+长锚杆计算结果(β=45°)Fig.15 Numerical calculation results of case 9 with three-bench excavation method and lengthened rock bolt (β=45°)

b.对于大变形而言，若仅强化支护结构或减小台阶开挖长度，可以减小围岩的位移；但多数情况下，支护结构依然会产生大变形破坏。

c.对于挤压因子较大的不明显挤压工况，采用常规支护+双台阶(短台阶)施工方法可以较好地控制围岩大变形；对于挤压因子较大的轻微挤压或挤压因子较小的不明显挤压工况，采用常规支护+三台阶施工方法可以较好地控制围岩大变形；对于挤压因子较小的轻微挤压工况，采用非对称锚杆支护+三台阶施工方法可以较好地控制围岩大变形。