跟踪微分器频率特性分析

牛宝良

（中国工程物理研究院总体工程研究所，四川 绵阳 621999）

数字微分计算是一种比较常用的运算，比如在速度计算、数字PID伺服控制中就要用到。简单的数字微分器是全频带的微分，在完成微分功能的同时，也会放大信号中的噪声，影响微分器的应用。韩京清等在1994年提出了跟踪微分器，具备了微分、降噪功能，但是此时的跟踪微分器还不完善，对于阶跃输入进入平稳期仍然有持续的震荡。韩京清等在1999年提出了跟踪微分器的离散形式，其实是一种改进版，彻底消除了震荡，这才具有了良好的工程应用性。此后，各种应用逐渐增多，也有多种不同的改进版本。文献[3]列举了4种版本，分别是开关型跟踪–微分器（STD）、快速型跟踪–微分器（FTD）、线性跟踪–微分器（LTD）、离散最速型跟踪–微分器（DFTD）。其中STD就是最早的版本，DFTD就1999年文献[2]提出的改进版。文献[4]提出了自适应TD。目前应用最多的还是DFTD，不特别说明的情况下，TD就是指DFTD。

TD的应用很多，涉及控制、信号处理等众多领域，也有一些关于TD频率特性的研究，这些文献揭示了TD的频率特性。比如无共振峰，高频段斜率是–40 dB/dec，转折频率附近相位滞后快速增加等，但是转折频率与TD的参数存在怎样的定量关系并未涉及。

在伺服控制系统中，通常用频率响应特性来描述系统的快慢。一个TD用于伺服控制系统，希望能准确知道它的频率范围，或者指定工作频带来设计一个TD，或者将一个TD用于信号分析与处理，也希望知道它适用处理什么频率范围的信号。本文将回答这些问题。

1 跟踪微分器方程

文献[2,6]都有较大篇幅介绍跟踪微分器，参数包括（速度因子），（滤波因子），积分步长。参考文献[6]，本文给出公式如下（文献中的变量、、，用、代替，取==）：

式中：为一个常数；为采样间隔，也是积分步长，s。

式中：、、、、、、是中间变量；()是输入信号；()是输入信号的跟随值，或者叫低频分量；()是()的微分，即速度；()是()的二次微分，即加速度；表示当前时刻，-1表示上一时刻。

把公式(2)用Simulink表达，如图1—3所示。其中in对应式（2）的()，acc对应式（2）的()。

图1 跟踪微分器的仿真模型Fig.1 Simulink model of TD

图2 acc Subsys模块Fig.2 Simulink model of acc Subsys

图3 w1 Sub模块Fig.3 Simulink model of w1 Sub

图1 与文献中的形式有所不同，实质未变，但是更容易分析其物理意义，而且通过仿真发现，这个形式在高频优于文献中的形式。首先，用代替以往文献中的、，取消，在这就是采样间隔。当系统的工作频率范围确定了，相应的采样间隔也就确定了，不用再与关联。其次，从图1可以看到，其实TD与单自由度系统的仿真模型形式上是相近的，参数实际是对计算的加速度进行饱和限幅，它具有加速度量纲。由于acc Subsys的输入是位移量纲，所以TD的与单自由度系统的弹簧刚度相当，因此有：

这样，就把与TD的工作上限频率联系起来了。

2 跟踪微分器频率特性分析

第1节建立了TD的参数与TD工作频率上限的关系，本节将通过仿真来验证这一关系。由于TD具有强的非线性特性，因此用时域仿真方法来验证。

2.1 仿真模型简介

建立的仿真模型如图4所示。频率发生器、波形发生器用来产生扫频信号及其对应的微分信号。TD为跟踪滤波器，输出、、acc值3个信号。平滑滤波器作为对照，也输出3个信号。平滑滤波器是一个阻尼比为1的低通滤波器，其共振频率取TD的3（仿真发现3倍与TD效果接近）。波形发生器生成信号（方波、正弦），也生成相应的理想微分信号。理想微分信号用来观察TD微分、平滑滤波器的误差情况。

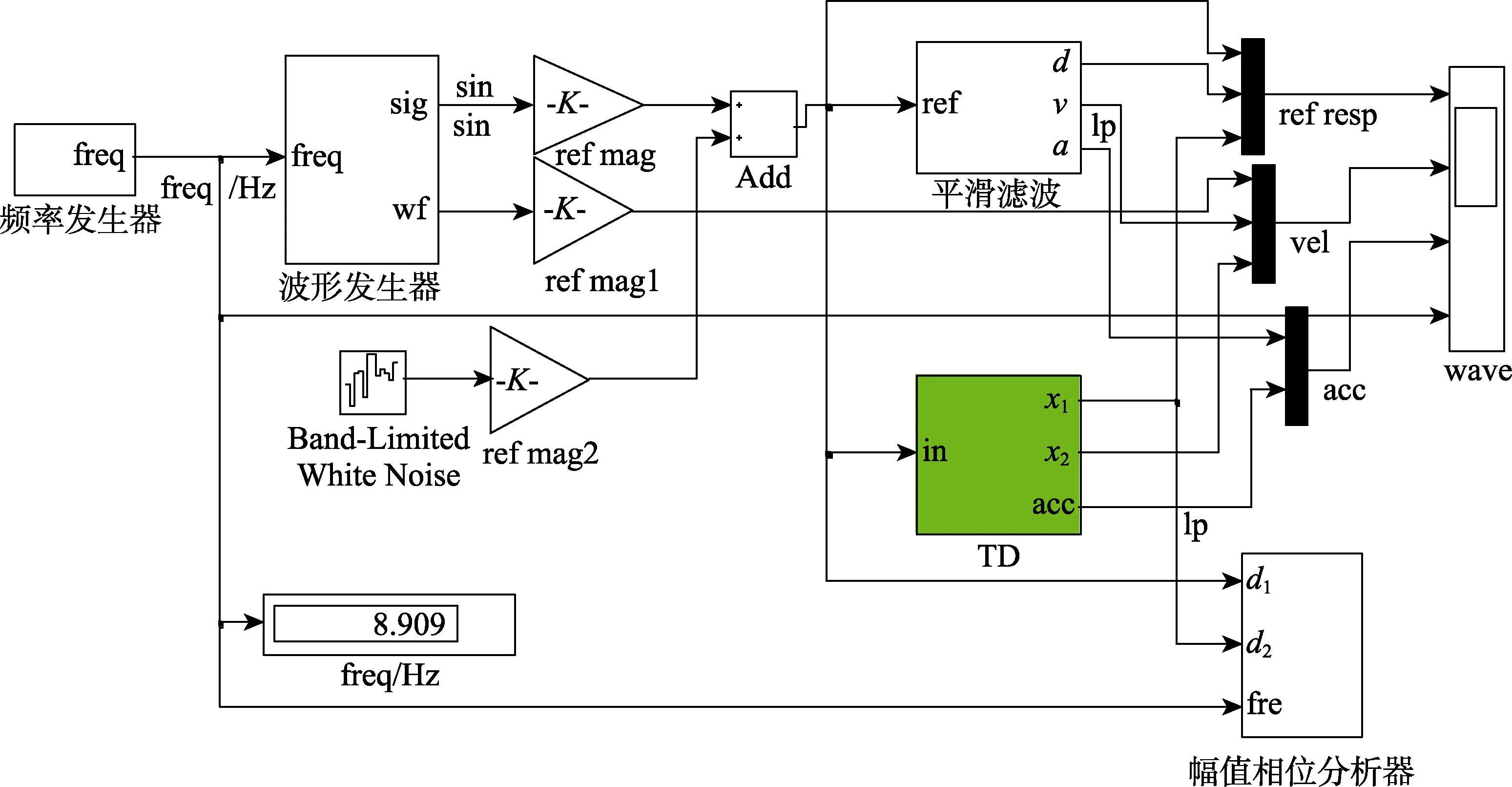
图4 扫频仿真模型Fig.4 Simulink model of sweep sin simulation

2.2 方波仿真

仿真采样间隔取50 μs。跟踪微分器的上限频率取10 Hz，=3 947.8。输入信号幅值为1，频率为4 Hz，仿真结果如图5所示。跟踪信号无超调达到目标值，TD得到的速度波形是规则的等腰三角形，即0速度起始，0速度结束，过程很平稳，它的加速度充分利用了限定的范围(－,)。在伺服控制器输入处，设置一个TD，它自动按限定的加速度范围给出最快过程曲线作为控制目标曲线。平滑滤波器也能在相近的时间无超调达到目标值，但是加速度已经超出范围。仿真表明，幅值为1、信号频率≤，都能很好地跟随。

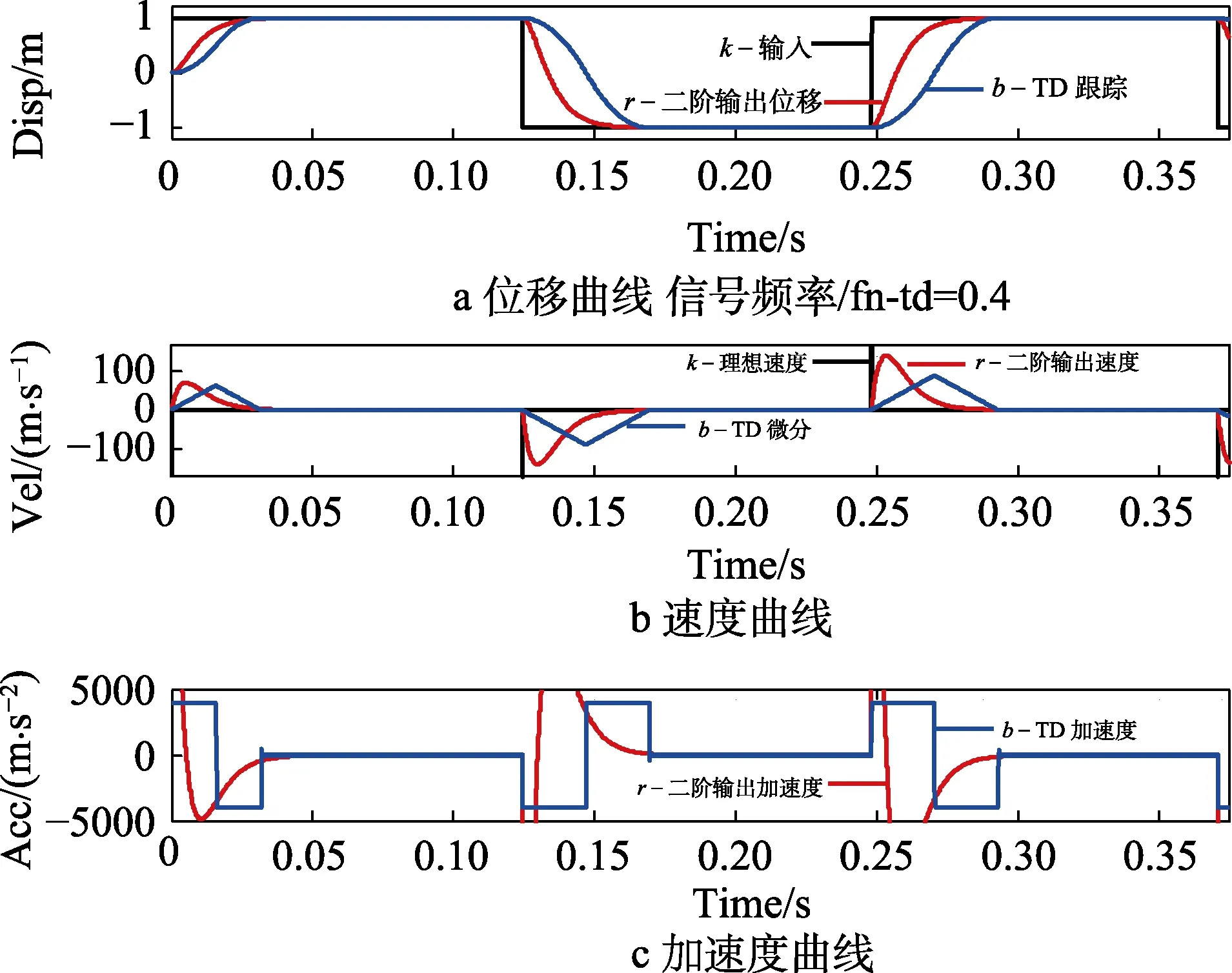
图5 TD方波仿真曲线Fig.5 Waves of square wave simulation on TD: a) displacement carve; b) velocity curge; c) acceleration curve

2.3 扫频仿真

TD参数取10 Hz，=3 947.8。输入信号幅值取0.1、0.25、1，频率取5~100 Hz，得到的频率特性曲线见图6，特征参数见表1。设置TD的频率上限为10 Hz，跟踪信号在10 Hz处幅值能保持1，跟踪信号与输入信号的相位滞后小于30°（10.37 Hz 滞后30°）。–30°~–90°是快速变化的，即设置10 Hz上限，TD就能工作到10 Hz。随着输入信号幅值的减小，幅频、相频的截止频率扩大了。0.25输入相比1输入时扩大了1倍，0.1输入相比1输入时扩大了3.16倍。从图6也可以看出，斜线是重合的，输入为1时的频率特性实际上是个包络，其他更小幅值的输入被限定到这个范围。当设置跟踪微分器的上限频率为其他值（不超过0.1 fs）时，所得的频率曲线也是与图6相似，即式（3）对于TD是普遍可用的。

图6 TD的频率特性（上限频率fn=10 Hz）Fig.6 Frequency characteristics of TD (fn=10 Hz): a) nonlinear frequency characteristics; b) phase frequency charactenistics

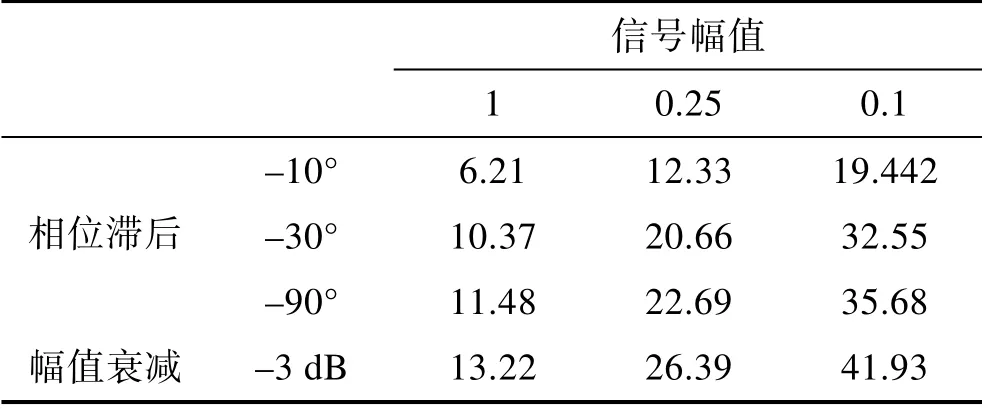
表1 不同输入幅值时的特征频率Tab.1 Characteristic frequencies of TD as different input magnitude Hz

信号频率等于TD上限频率时的时域曲线如图7所示。1 V输入时，TD跟踪信号与输入信号有明显可见的滞后，但是优于平滑滤波器（截止频率为3）输出；微分信号滞后也小于平滑滤波器微分输出，但是波形有失真，这是它相位上优于平滑滤波器微分输出的代价。在加速度波形上，两者的区别特别显著。0.1 V输入时，TD跟踪信号与输入信号重合，平滑滤波器输出则有明显滞后；TD的微分信号也是与理想微分信号也是重合的；在加速度波形上，TD的加速度在峰顶峰谷有毛刺和跳变，平滑滤波器输出则是规则正弦。这是TD相比平滑滤波器的优点，信号幅值减小时，频带扩大。

图7 信号频率等于TD上限频率fn时的时域曲线Fig.7 Time waves while sin wave signal frequency equal TD fn: a) input 1 V; b) input 0.1 V

2.4 含有噪声时仿真

实际信号中常常含有噪声。为此，加入一定的白噪声，来观察效果。图8a的信号频率比较低，为TD上限频率的1/2，TD跟踪幅值好，相比平滑滤波器输出占有优势。图8b信号频率达到TD上限频率，TD跟踪幅值较好，但是相位反而滞后平滑滤波器（无噪声时相位是优于平滑滤波器，可见噪声带来了不利影响）。从加速度曲线可以看到，正常情况下加速度直接到负最大或正最大，由于噪声影响，从负最大到正最大震荡一段时间才能保持在正最大。图8c的信号频率也TD上限频率的1/2，信号幅值减小到0.1，输入信号的信噪比很差，出现一个比较反常的现象，TD跟踪信号、TD微分信号上出现了一个震荡信号，震荡信号的幅值与有用信号相当，而平滑滤波器的跟踪信号、微分信号更好。

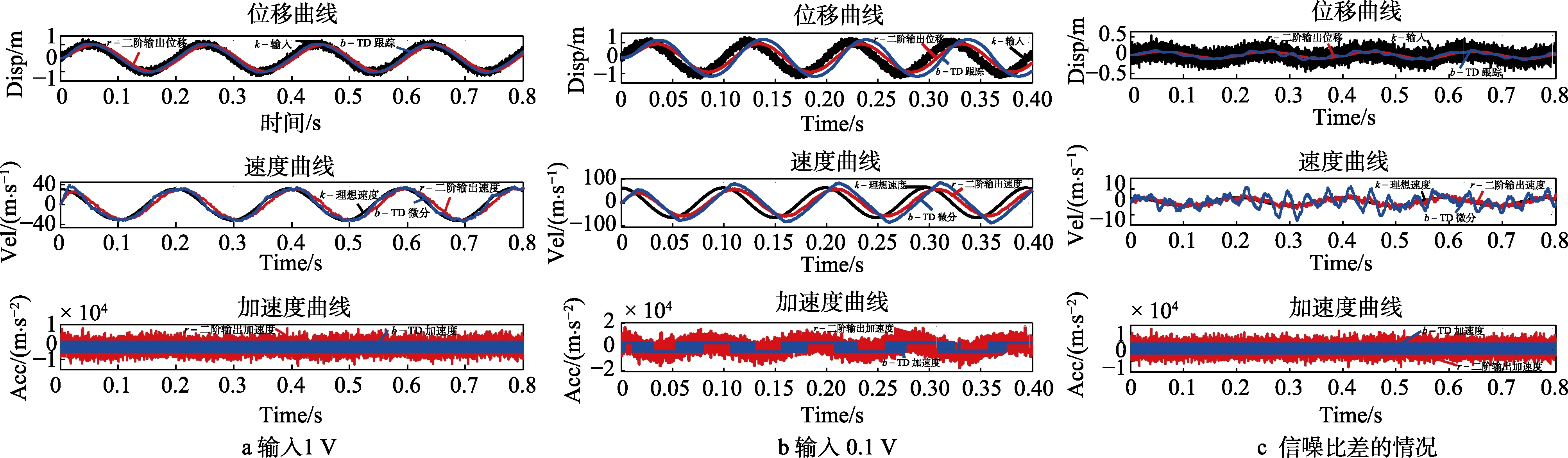
图8 有噪声信号频率等于TD上限频率fn时的时域曲线Fig.8 Time waves with noise while signal frequency equal TD fn: a) input 1 V; b) input 0.1 V; c) poor signal-to-noise ratio

3 跟踪微分器的应用

第2节已经分析得到，TD的上限频率与有关，同时还与输入幅值有关。对于输入为1的TD，上限频率与满足式（3）。在工程应用中，假设输入信号的范围是±，在TD的前后分别加一个比例环节，TD前的比例是1/，TD后的比例是。这样，既能满足输入信号范围，又能满足指定的频率范围。

关于的取值，其实与TD的关系不大，通常由伺服控制系统的上限频率决定。假设伺服控制系统的上限工作频率为，则数字伺服控制系统的采样频率、采样间隔由式（4）计算得到。

4 减小跟踪信号滞后的改进

TD生成的跟踪信号，总是存在一定的滞后，信号频率/TD上限频率越大，滞后越大。在仿真中发现，一个小小改进可以减小1拍的滞后。如图9所示，从积分器（integrator1）输出再接一个积分器（integrator3），积分方式选为后向欧拉法，用它来替代，比原可以提前1拍。仿真结果如图10所示，采样频率为100 Hz，TD截止频率为5 Hz，输入方波频率为1 Hz。

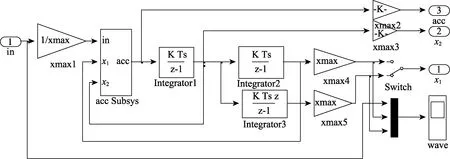
图9 改进后的TDFig.9 Improved TD

图10 改进后TD 的跟踪信号与原信号比较Fig.10 Compare wave of improved TD with wave of TD

5 结论

本文研究了TD的频率特性，提出了输入幅值为1时频率上限与TD参数之间的关系。通过时域仿真验证了该关系的正确性，解决了定量确定TD的参数问题。

TD的频率特性随输入信号幅值的改变而变化，幅值越小，频带越大，高幅值的幅频曲线包络低幅值的幅频曲线。对于输入幅值不是1时，宜进行归一化处理，在TD之后再恢复原量级，这样可以达到跟踪微分的目的，同时带宽刚刚好，因此滤波效果好，抑制噪声最佳。

信号频率小于TD的上限频率时，幅频、相频特性都比较好。输入幅值为1，信号频率等于0.62时，相位滞后不大于10°；信号频率等于时，相位滞后26°。相频曲线在1.1附近呈现快速变化的特征，1.15时滞后达90°。因此，建议信号频率在0~0.62为佳，最多取到0~。在微分信号后新增一个后向欧拉积分器，可以获得跟踪信号在相位上提前1拍的效果。多数情况下，TD的幅频、相频优于平滑滤波器，但是在信噪比很差时，平滑滤波器反而优于TD。

综上所述，明确积分步长与系统采样间隔相一致，建立参数与TD工作频率上限之间的关系后，将极大方便TD的设计，也将推动TD更多应用。