跨介质航行器高速斜入水跳弹现象研究
2022-06-07周可黄振贵陈志华刘想炎王浩
周可,黄振贵,陈志华,刘想炎,王浩
(南京理工大学 瞬态物理国家重点实验室,南京 210094)
随着跨介质航行器的发展,近来越来越多的国家开始研究跳弹现象,能在飞行过程中反复出入水面,对作战计划的隐蔽性有很大的提升。跳弹现象也已经在军事上得到应用,也就是“跳弹桅顶轰炸”。早在二战时期,W.Barnes就利用跳弹轰炸德国鲁尔水坝,随后在太平洋战争中,美国也效仿英国的跳弹,对日军舰队进行轰炸。相比于高空投射,低空的跳弹有着更好的隐蔽性和精准性,因此航行器的跳弹现象也得到了更大的关注,如果能较好地掌握这一现象的规律,就能开发出一种突防能力更好武器。
入水问题的研究最早开始于19世纪末,Worthington等利用闪光照相机对刚性球体垂直入水过程中发生的一系列现象进行了试验研究。对于物体入水稳定性方面的研究,侯宇等通过试验探究了射弹小角度高速入水时产生的超空泡对射弹的弹道轨迹的影响,以及高负载对弹体的损伤。胡青青探讨了4种头型、3种长径比射弹高速入水时的稳定性和空泡形态,并分析了其对入水过程的影响。黄鸿鑫等通过数值模拟方法,从空泡形态、速度衰减以及俯仰角变化探讨了射弹头部形状和质心位置对高速入水稳定性的影响。郑磊基于STAR-CCM+和ABAQUS联合仿真对弹体进行了垂直和倾斜入水双向耦合计算,分析了在入水过程中弹体的动力学特性、弹体表面变量以及应力应变情况。
跳弹现象则是物体入水失稳方面的一种表现,对于跳弹问题的系统性研究最开始以刚性球体为研究对象。Richardson研究了圆球倾斜入水跳弹的问题,讨论了当球体倾斜入水后弹跳时所涉及的机制和力。Miloh等通过数学方程的推导得出了椭圆球体入水发生跳弹的临界角的经验表达式。Soliman等用钢球和硬铝球射入浅水深度和干沙中,总结了不同介质下跳弹发生的临界角,临界角随着速度的增加而减小,但存在一个截止角,在任何速度下都不会发生弹跳。Johnson探究了旋转和非旋转球形弹丸对跳弹行为的影响。随着研究的进一步深入,圆柱体以及射弹等回转体的入水跳弹现象开始被关注。Nguyen等通过数值模拟计算,探究了圆柱体入水时的角度和速度对跳弹行为的影响,总结出了每个入水角都有一个临界速度发生跳弹。Hutchings提出了一种弹跳理论,该理论允许考虑弹丸自旋的影响,计算了球体和旋转圆柱体的弹跳临界角,并将旋转圆柱体的理论应用于第二次世界大战期间开发的“巴恩斯·沃利斯”跳弹炸弹。Moxnes等通过试验分析和数值模拟计算总结了不同类型的射弹在水中发生跳弹的规律。Gold等利用UZI冲锋枪发射9 mm子弹,探究了相同速度下不同角度子弹高速入水下的跳弹规律。
综上所述,目前对于物体跳弹现象的研究着重于球体、圆柱体和射弹,而对航行器入水时发生跳弹现象的研究还较少,特别是高速入水。公开的文献仅有Chen等通过数值模拟计算了不同头型的航行器入水后的跳弹行为,得出锥鼻形头部更容易改变轨迹。袁绪龙等提出了跨介质航行器高速入水过程中产生的巨大法向过载和弯矩。李永利等利用数值模拟技术研究了航行器在不同顶角下小角度低速入水时的跳弹现象。陈国明等通过试验和数值仿真研究了航行器发生跳弹现象的条件和规律。本文通过数值模拟方法,模拟了航行器在高速斜入水后产生跳弹现象的运动过程,讨论并分析了不同入水角、不同速度对高速倾斜入水时航行器跳弹行为的影响,揭示产生跳弹的机理,为航行器高速入水跳弹的设计提供参考。
1 数值计算理论
1.1 流体基本控制方程
VOF多相流模型是建立在欧拉网格下的界面追踪方法。该方法中,互不相容的流体组分共用一套动量方程,并通过引入相体积分数这一变量来实现对计算域内相间界面的追踪,更加适用于捕捉流体自由面的变化和求解气液相的比例。其中表示相的体积占所在网格体积的比值,0表示为空气相,1表示为水相,0<<1表示为交界面。VOF方法就是通过求出整个计算域内各网格单元的相分数,从而构建出界面,如图1所示。

图1 VOF交界面示意图Fig.1 Interface of the VOF: a) phase fractional spatial distribution; b) interface reconstruction
对于每个控制单元,其连续性方程为:

式中:为整体网格单元内的平均数学密度。VOF多相流模型中,密度的定义为=+,和分别为空气和水的密度,和为水和空气在单元格的密度。
动量守恒方程为:
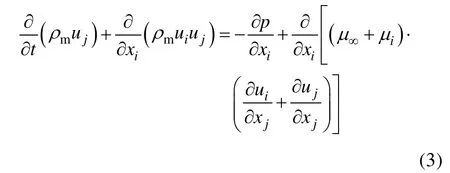
式中:为网格单元的动力黏性系数;为网格单元的湍流黏性系数,=+。
两相之间采用的质量传输方程为Schnerr-Sauer空化模型。该空化模型的计算效率高,稳定性强,模拟效果好。相关计算表达式为:
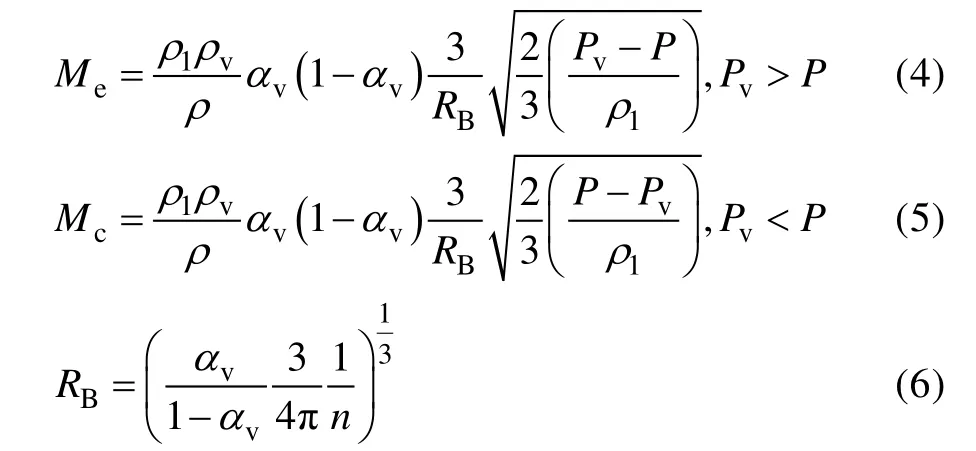
式中:分别代表蒸发率和冷凝率;、分别为蒸汽相的体积分数和密度;为气泡半径;为单位体积空泡数。
1.2 湍流模型
采用Realizable-模型,它是基于标准-模型发展而来的,基本思想和-模型一致。其用某种数学方式建立湍动黏度和湍动能以及湍流耗散率的数学联系,并分别以湍动能和湍动耗散率建立运输方程,最终实现方程的封闭。
湍动黏度的表达式为:


湍动能和湍动耗散率的输运方程为:

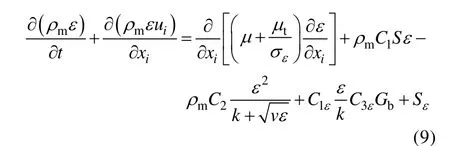

1.3 六自由度弹道模型
本文利用DFBI模块耦合重叠网格模拟刚体复杂的六自由度运动。在全局惯性坐标系下,刚体绕质心的运动方程为:


在局部坐标系下,DFBI旋转运动方程为:

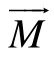
1.4 重叠网格技术
重叠网格技术是对计算区域和部件区域单独划分设计网格,主要由背景网格和组件网格相互重叠而成,如图2所示。两者之间会有一部分重叠区域,但不存在连通关系,在初始化的时候会进行布尔运算,计算域外的网格会被删除并排除在外,使该部分网格不进行数据交换。根据布尔运算剩余的重叠网格区域,建立插值关系,并且建立相应的数学关系进行数据交换。相比动网格技术中持续的网格更新,重叠组件中组件网格随物体一起运动,不需要网格变形,也不需要重新生成网格,只需要定义组件运动规律和网格重叠边界条件,即可实现对物体在流域中运动的流体力学问题的模拟,避免因网格变形、网格单元生成或消失带来的计算误差,具有较大的优越性。

图2 重叠网格插值示意图Fig.2 Overset interpolation diagram
2 数值模拟方法
2.1 计算模型
计算模型的几何尺寸如图3所示,全长=1.28 m,弹径=0.128 m,质量为16.991 kg,分布均匀,头部为30°的拱形,尾部为线性截断体。

图3 航行器物理模型Fig.3 The physical model of the vechicle
采用的计算软件为STAR-CCM+,基于N-S方程,选用Realizable-湍流,欧拉多相流模型,用VOF流体域体积模型捕捉自由液面的变化和Schnerr and Sauer空化模型模拟空化过程,引用重叠网格技术耦合六自由度方程来捕捉航行器的入水运动。为了减少计算量,本文预估了航行器的大致轨迹,并在轨迹附近的网格进行加密作为计算域。网格截面如图4所示,轴由纸面向外。计算域如图5所示,长10,宽3.9,水域深2.7,空气域为1.2。计算域四周以及底部为压力出口,压力根据水深依据公式=设置,顶部设置为速度进口,速度幅值为0。湍流运输方程采用二阶迎风格式,-湍流求解选用STAR-CCM+内嵌的AMG线性求解器,松驰方案选用高斯–赛德尔。时间上采用隐式非稳态,时间步长为2×10s。分别对航行器在初始入水角为15°和入水速度为100、150、200 m/s,以及初始速度为150 m/s,入水角为8°、15°、25°一共5个工况进行数值模拟计算。

图4 Z=0截面网格Fig.4 Schematic diagram of Z=0 section mesh
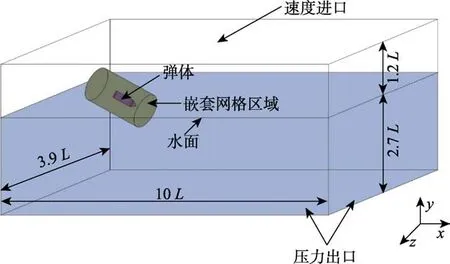
图5 计算域及边界条件设置Fig.5 Computational domain and boundary condition settings
2.2 数值计算方法验证
为了验证本次数值模拟方法的有效性,本文选取参考文献[22]中的试验结果作为对照。本次验证模型采用文献中直径为6 mm、长为24 mm的回转圆柱体,质量为4.88 g,入水速度为106.6 m/s,水箱尺寸为310 mm×310 mm×660 mm,水深为600 mm。在数值模拟中,模型质量、几何尺寸、入水速度与试验保持一致。通过对比圆柱体的速度衰减和位移变化以及不同时刻的空泡演化来验证模拟的有效性。
速度曲线的数值模拟和试验结果对比如图6a所示,最大误差约在5%,并且在入水时刻速度的剧烈变化,数值模拟能很好地捕捉。圆柱体的位移变化曲线如图6b所示,最大误差也约在5%,在误差允许范围之内。
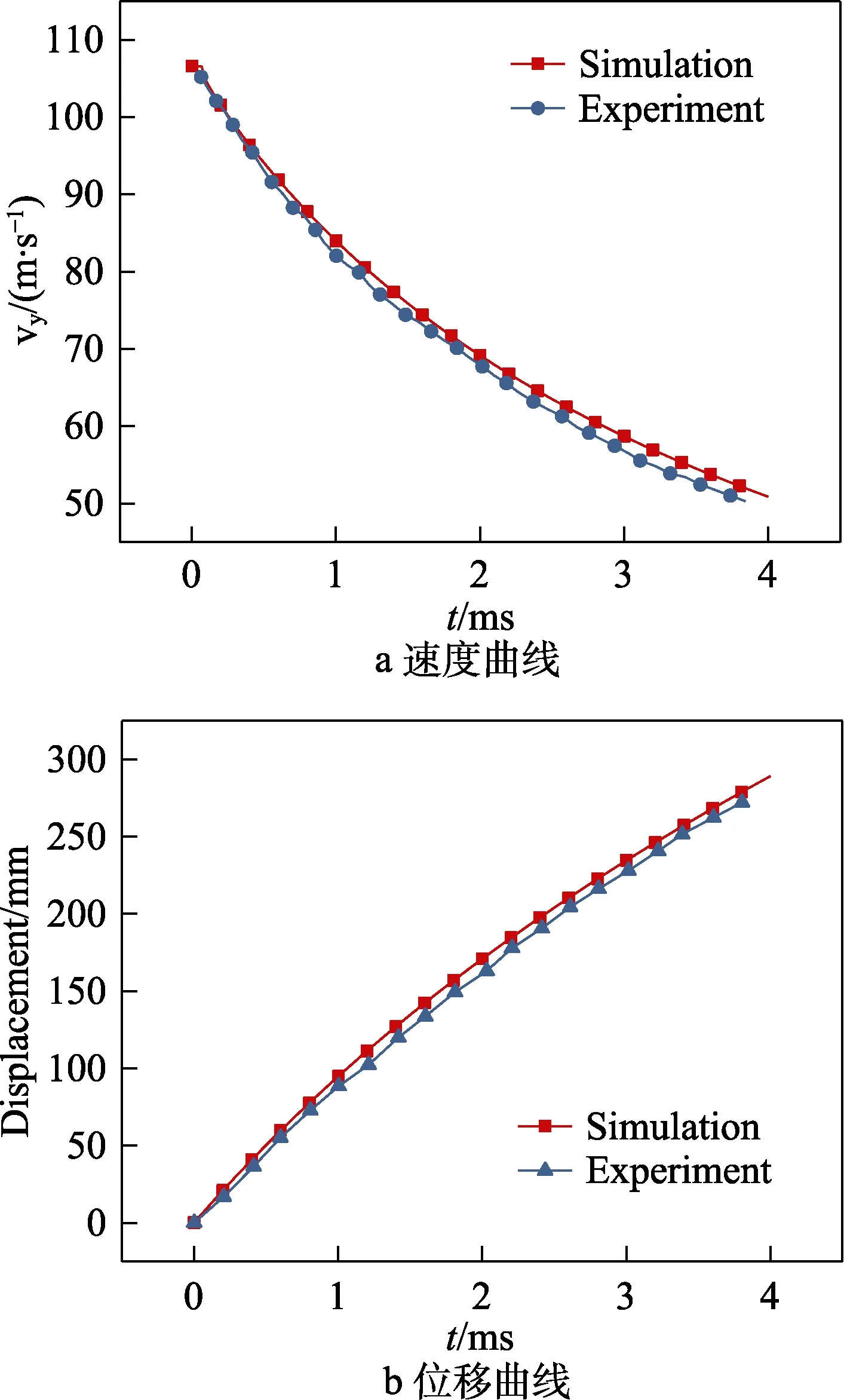
图6 试验数据与模拟数据对比Fig.6 Comparison of experimental data and simulation data:a) velocity curve; b) displacement curve
圆柱体入水时在=0.8 ms和=2 ms空泡轮廓的对比如图7所示。图7清楚地展示了空泡的产生以及闭合2种状态。在=0.8 ms时,空泡完全包裹了圆柱体。随着圆柱体继续的下落,空泡逐渐的被拉长。在=2 ms时,空泡出现了闭合。通过与试验图像的对比可以发现,模拟结果与试验结果较为一致,进一步验证了模拟方法的有效性。

图7 空泡演变图Fig.7 Cavitation evolution: a) experiment; b) simulation
为了避免网格数量对计算结果产生的影响,在数值计算之前建立了3种不同的网格密度来对网格无关性进行检验。基于不同网格密度计算下航行器入水深度的变化曲线如图8所示。可以看出,在下潜阶段,网格密度的影响不大,在后期上升过程中,不同网格密度之间有一定的差距,随着网格的加密,差距也越来越小。网格数量330万以上的时候,曲线几乎重合,相差较小。从计算成本和计算结果的准确性综合考虑,本文采用330万网格数量进行数值计算。
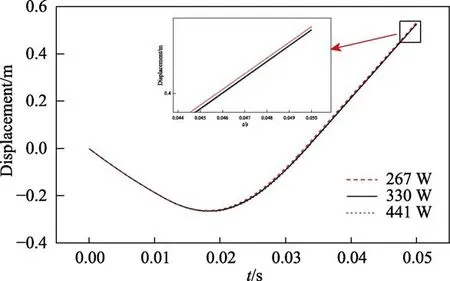
图8 不同网格密度下航行器深度变化Fig.8 Vehicle depth variation at different mesh densities
4 结果及讨论
4.1 航行器跳弹机理分析
通过数值模拟计算航行器在150 m/s,入水角为15°工况下的跳弹现象来阐述跳弹发生的机理,整个跳弹现象过程如图9所示。首先,航行器的头部接触水面时,头部会受到很大的冲击载荷,同时产生喷溅和溅水。因为航行器头部为卵圆形,使得头部两侧受力不均匀,其中下半部远大于上半部,以此产生对航行器较大的俯仰力矩,如图10所示。此力矩会使得航行器产生一个逆时针方向的俯仰角速度,它随时间的变化曲线如图11所示。可以看出,俯仰角速度在入水后呈现增加的趋势,且方向一直为正方向,航行器的俯仰角增大,弹道发生弯曲。航行器头部沾湿面积逐渐增加,使得航行器受到的流体动力变大,俯仰力矩持续增加。随着航行器继续前行,在=0.128 s时,尾部也开始出现沾湿。因为头部和尾部的沾湿面出现在质心两端,所以两端对质心的力矩是反向的,使得航行器在该节点出现力矩减小,致使角速度也减小。最后航行器两端都受力的情况下达到力矩平衡,维持在386 N·m左右。此后俯仰角速度大小呈平稳增长趋势,航行器以较为平稳的速度抬升,然后冲出水面。当航行器头部离开水面瞬间,头部受到的流体动力消失,俯仰力矩开始迅速减小。

图9 航行器入水出水过程Fig.9 Schematic diagram of the process of entering and exiting water of the vehicle

图10 俯仰力矩变化曲线(v=150 m/s,α=15°)Fig.10 Change of pitch moment curve (v=150 m/s, α=15°)

图11 俯仰角速度变化曲线(v=150 m/s,α=15°)Fig.11 Change of pitch angular velocity curve(v=150 m/s, α=15°)
通过上述分析可将航行器的跳弹运动过程分为3个阶段:第一阶段为入水,航行器头部撞击水面,头部下缘受力,给航行器一个逆时针方向的俯仰力矩;第二阶段为浸水,此时航行器两端的沾湿面积逐渐增加,使得航行器俯仰力矩出现微波动直至稳定;第三阶段为出水,此阶段航行器俯仰力矩维持稳定,航行器以较为平稳的速度冲出水面。
从图9可以看出,航行器的空泡经历了入水撞击、空泡形成、开空泡和空泡闭合几个阶段。航行器头部撞击液面,形成了不对称空泡。这是因为撞击水面时,下表面的沾湿面积大于上表面,所以下表面的空泡形成快于上表面,同时尾部只有下表面沾湿,使得航行器两侧受力不同。随着航行器的姿态和运动轨迹的变化,空泡变得越来越不对称。同时,可以观察出空泡呈现先扩张、后收缩的趋势,空泡后半段在扩张到最大直径后,水压开始挤压空泡壁,空泡收缩并开始闭合。
4.2 航行器初速度对跳弹行为的影响
航行器在不同入水速度下水相的变化如图12所示。从图12中可以直观地看出3种工况下航行器在水中发生跳弹的全过程对比,不同速度下航行器的出水时间有着明显区别,随着速度的增加,出水时间节点就越早。其深度和水平位移如图13所示(图13b中箭头标注为航行器出水时间节点),也能看出3种入水速度下出水时间的差异,并且航行器最大下潜深度随着速度的改变变化不显著,但出水时的水平位移随着速度的增加而减小。速度的变化趋势如图14所示,不同入水速度下速度变化的斜率有所不同,初始速度为200 m/s的速度变化最快。由表1可知,虽然三者速度改变的快慢不同,但是在出水时它们的出入水速度比几乎一致,这是由于它们出水时间不一致所致。
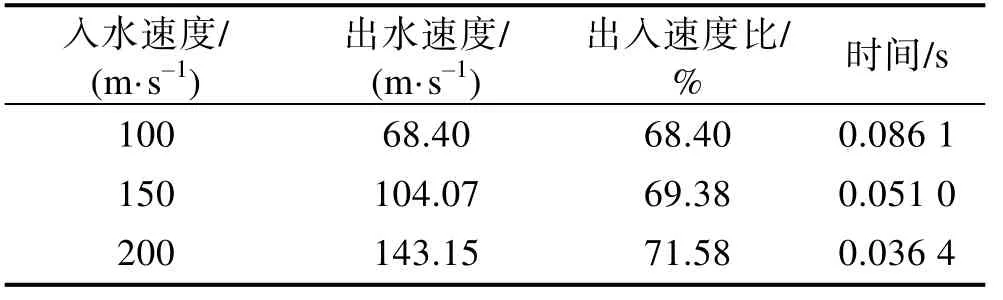
表1 不同入水速度下入水出水速度、时间变化Tab.1 Change of water inflow and outflow speed and time under different water entry speeds
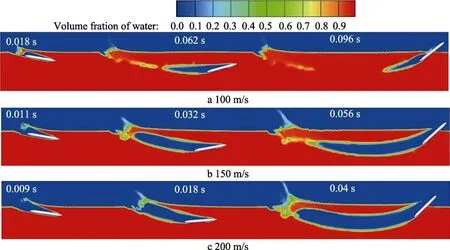
图12 不同速度工况下的水相图Fig.12 The water phase diagram of different speed conditions
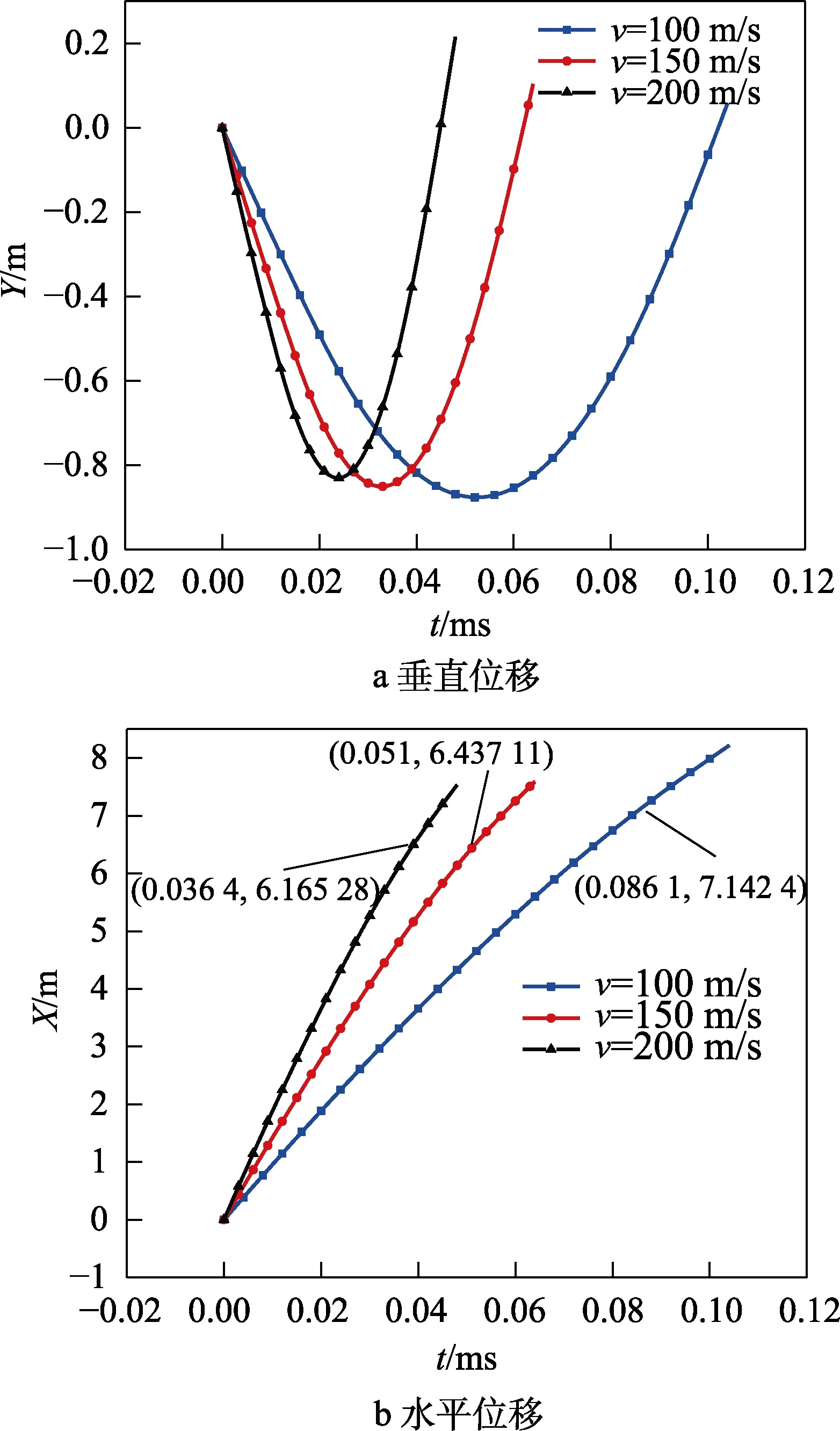
图13 不同速度工况的位移变化曲线Fig.13 Change of displacement curve under different speed conditions a) Vertical displacement; b) Horizontal displacement

图14 不同速度工况的速度变化曲线Fig.14 Change of velocity curve under different speed conditions
俯仰力矩的变化如图15所示。可以看出,入水阶段的俯仰力矩峰值随着速度的提升而明显增加,在从浸水阶段进入出水阶段的过渡时间明显缩短。初始速度越快,在该阶段越能快速稳定俯仰力矩,这有利于缩短出水时间。最后在出水阶段时,俯仰力矩随着速度的增加而提升。俯仰角速度变化的如图16所示。不同速度工况下,除了在浸水阶段俯仰角速度有一小段下降外,在出水前的其他时间段呈增加趋势。这是因为尾部受力增大,使得俯仰力矩为负,从而使得俯仰角速度减小。最后俯仰角速度发生骤降,标志着航行器头部已经离开了水面。由此可知,入水速度对跳弹现象有着明显的影响,并且可推测当初始速度低于某一临界点时,航行器在该角度就无法跳出水面。

图15 不同速度工况下俯仰力矩的变化曲线Fig.15 Change of pitch moment curve under different speed conditions
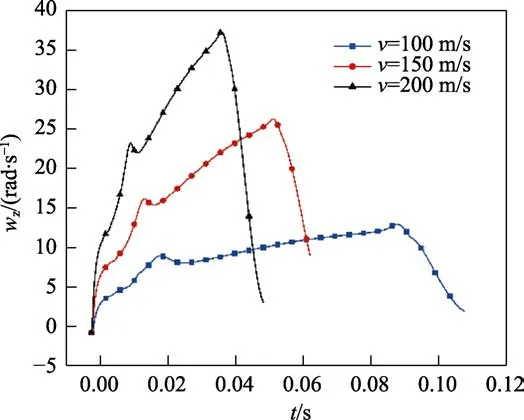
图16 不同速度工况下俯仰角速度的变化曲线Fig.16 Change of pitch angular velocity curve under different speed conditions
4.3 不同入水角对跳弹行为的影响
在航行器初始速度为150 m/s下研究入水角对跳弹行为的影响,其仿真结果水相图如图17所示,俯仰角角度大小变化如图18所示。可以看出,随着航行器入水角的增大,最后出水时的角度也有着明显增大。由表2可知,入水角越大时,角度改变量也会明显增加。
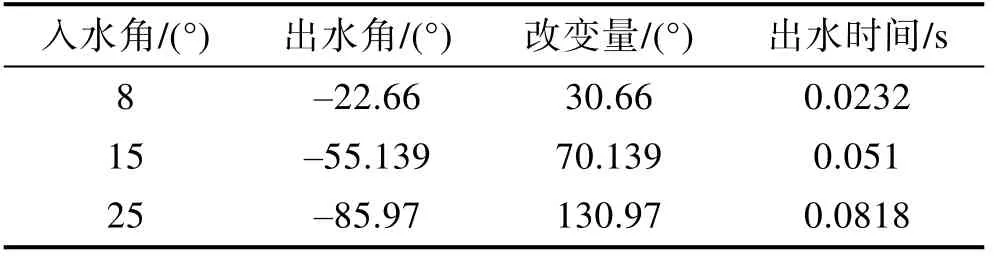
表2 不同入水角入水出水时角度的变化量Tab.2 Variation of angle when entering and exiting water at different entry angles
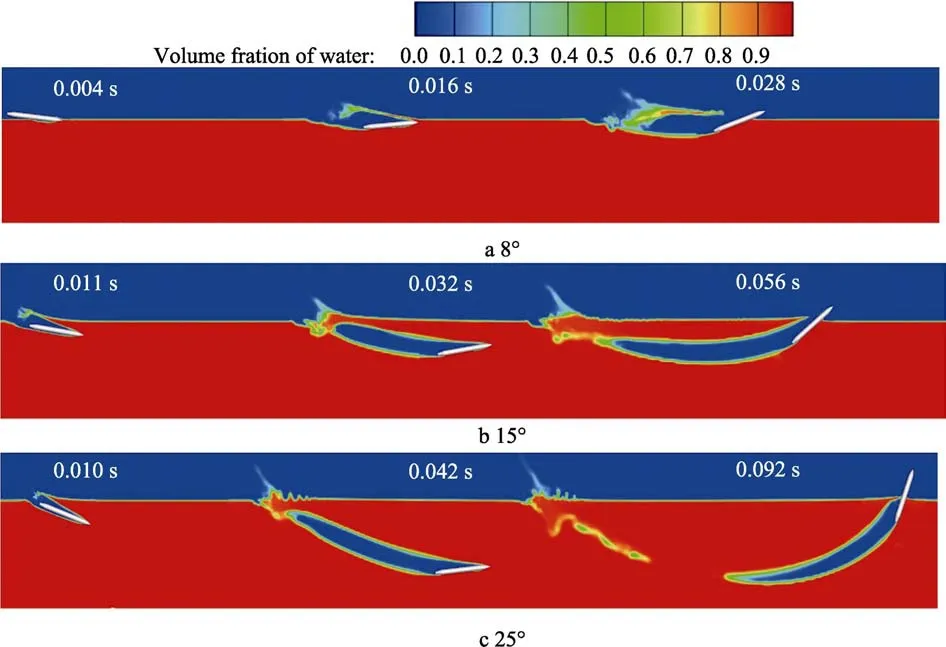
图17 不同入水角度工况下的水相图Fig.17 Water phase diagrams at different water entry angle angles

图18 不同入水角度工况下俯仰角的变化曲线Fig.18 Change of pitch angle curve under different water entry angle conditions
不同入水角下航行器质心垂直位移和水平位移变化趋势如图19所示。从图19a可以看出,3种入水角中,航行器质心垂直位移有着较大差异,其中25°入水角的最大垂直位移几乎为8°入水角的8倍。图19b中,3种工况在出水前的水平位移较为一致,但是因为出水时间的不同,使得它们的出水点位移有着较大差别,入水角为8°、15°、25°对应的出水点位移分别为3.31、6.43、8.78 m。由此可知,入水角度对航行器下潜深度的影响比初始速度大。
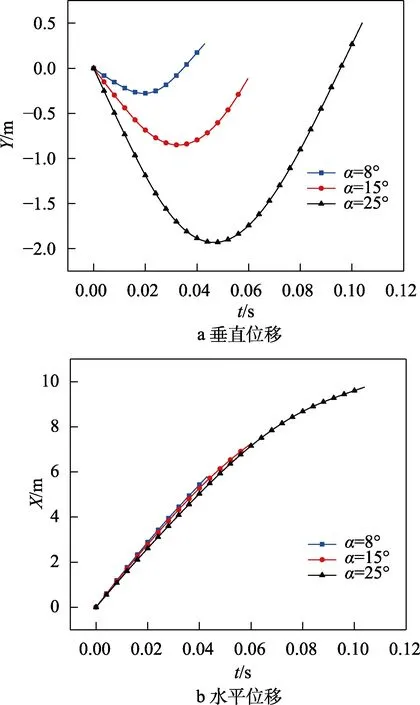
图19 不同入水角度工况下位移的变化曲线Fig.19 Change of displacement curve under different water entry angle conditions
进一步分析不同入水角带来的差异性。入水瞬间,25°和15°入水角工况的俯仰力矩峰值相差不大,但是都远大于8°的工况。在浸水阶段,不同角度的俯仰力矩变化趋势几乎一致,在该阶段不同角度的俯仰力矩几乎都维持在386 N·m,而8°入水角的浸水阶段时间较短,俯仰力矩还未稳定就进入了出水阶段,离开水面。从图21也能看出,这一阶段俯仰角速度的增加较为匀速,航行器偏转较为平稳。航行器在刚入水时,角速度迅速增加,当尾部触碰空泡壁沾湿后,3个工况角速度均出现下降过程。随着航行器姿态的改变,入水角为15°和25°的工况,航行器头尾两端作用力相互作用,使得力矩稳定,角速度平稳增加,直至最后离开水面;而入水角为8°的工况因为没有经过力矩平衡这一过程,在角速度下降后,又迅速增加,然后离开水面,整个过程中角速度大小随入水角的减小而增大。
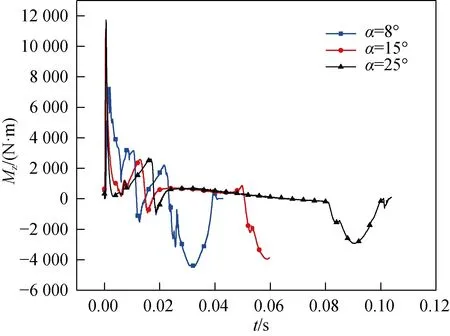
图20 不同入水角度工况下俯仰力矩的变化曲线Fig.20 Change of pitch moment curve under different water entry angle conditions

图21 不同入水角度工况下俯仰角速度的变化曲线Fig.21 Change of pitch angular velocity curve under different water entry angle conditions
5 结论
本文采用数值模拟的方法对跨介质航行器的小角度入水的跳弹过程进行了研究,分别研究了入水速度和入水角的变化对跳弹行为带来的影响,分析对比了不同工况下航行器的位移、俯仰力矩和俯仰角速度变化以及出水时间的差异,得到以下结论:
1)航行器高速入水时,发生跳弹的主要原因是航行器上下以及头尾两侧受力不均,形成了向上的偏转力矩,改变了航行器的俯仰角,会形成不对称空泡。整个跳弹过程可以分为入水阶段、浸水阶段和出水阶段3个阶段.
2)相同入水角,不同入水速度下,速度越大,越容易发生跳弹现象,出水时间也越早,航行器出水时的速度约为入水速度的70%。航行器在水中下潜的深度受速度的影响不大,但是在出水点位移随着速度的增加而减小。入水速度越大,航行器所受到到的俯仰力矩越大,俯仰角速度越大。
3)相同入水速度,不同入水角工况下,入水角越小,越能促进跳弹行为的发生,航行器出水时角度改变量越小。入水角的改变对航行器位移的变化更加明显,随着入水角的增加,航行器的下潜深度和出水点位置也随之增大。
