基于高阶复合曲面单元的非均匀大薄板装配偏差计算模型

厚度非均匀分布的非规则大型薄壁结构件具有重量轻、强度高等优点，广泛运用于航空航天、船舶等领域.非规则大型薄壁结构件的几何特征造成其结构刚度的非均匀分布，在加工和装配过程中易产生变形以及转动耦合的非线性翘曲变形，导致结构存在较大偏差.结构的复杂性使得利用解析法求解其非线性变形十分困难.而在数值仿真中，为满足精度要求，传统有限元法受单元线性假设限制，离散结构需要大量单元而导致计算效率低.因此，针对非规则大型薄壁结构，构建合理的高阶单元模型以及采用有效的结构离散方法是描述其翘曲变形并提高计算效率的关键.

非均匀大型薄壁结构的变形和应力的高精度分析一直是其制造偏差精确计算的难点.现有有限元法主要采用三维实体单元模型或基于板壳理论的二维壳单元模型对结构进行离散.三维实体单元能够精确计算结构变形及力学特性，但对存在凸台和承受弯曲变形区域的计算效率低；二维壳单元的单元自由度和数量较少，计算效率较高，但忽略了截面变形且用于厚度非均匀结构的建模存在局限.

利用等效单元法和复合单元法可以解决壳单元离散的局限性并减少单元数量.等效单元法通过内力等效将附加厚度结构的作用等效至主体结构，但无法描述两者之间的变形耦合；复合单元法将主体及附加厚度结构等效为单元叠加，通过单元间变形协调及连续性条件构建复合单元模型.针对板类结构，Carrera总结了两种常用的板壳叠层结构建模方法, 其中假定各层单元均以单层板形式变形的单一板模型忽略了柔性结构的非线性大变形特征，Layer-wise模型(一种预训练语言模型)通过在各单层板接触界面处插入高阶边界条件提高计算精度，但结构自由度的增加导致计算效率低，且该模型常用于复合材料结构建模及变形计算.目前的复合单元主要基于小变形和小转动假设，在针对大变形和大旋转的非线性问题方面，Shabana等提出绝对节点坐标法(ANCF)，用斜率坐标替代传统的转角来精确描述单元截面变形，并提出非线性弹性力和大变形的计算方法；Matikainen等通过在厚度方向引入二阶位移插值构建高阶ANCF板单元，克服了弯曲产生的泊松锁定；Ebel等通过增加单元节点消除前者产生的附加剪切锁定现象，提高了计算精度.Abbas等通过修正板单元的形函数构建变厚度的板单元模型，消除了ANCF对规则单元模型的限制，并利用模态分析以及ANSYS软件的对比结果验证了单元模型的正确性.基于复合单元法，Yu等考虑板单元间接触界面的变形协调条件，构建全参数的板/板单元模型来离散含筋板结构，消除了筋板穿透现象且具有较高的计算精度，但该单元在描述弯曲单元时会产生泊松锁闭问题.现有的ANCF单元主要用于离散厚度非均匀的规则薄壁结构或单一厚度的非规则薄壁结构，而针对厚度非均匀且形状非规则薄壁结构离散的高阶单元模型研究较少.

基于ANCF，构建非规则高阶曲面复合单元模型并计算单元非线性刚度矩阵，精确描述结构的非线性翘曲变形；利用非规则高阶曲面单元及复合单元组合离散非规则大型薄壁结构，解决不同厚度单元间节点连接和变形耦合问题；基于连续介质力学建立非规则薄壁结构装配协调变形计算模型.对重型火箭箱底瓜瓣结构进行装配偏差变形计算仿真，并研究边缘加厚区域尺寸对瓜瓣装配偏差和结构刚度的影响.

1 非规则高阶曲面复合单元建模

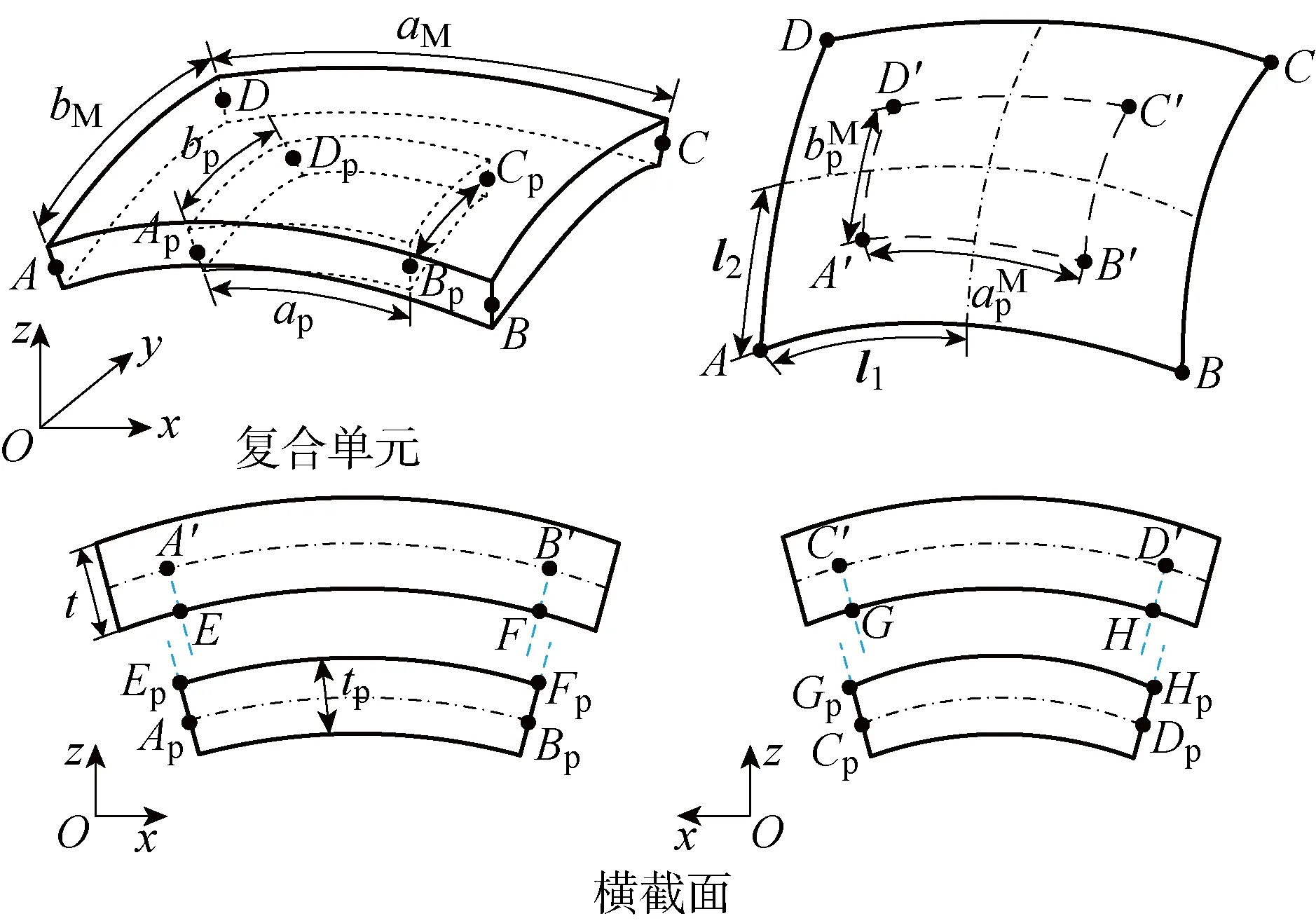
1.1 非规则大型薄壁结构离散方法

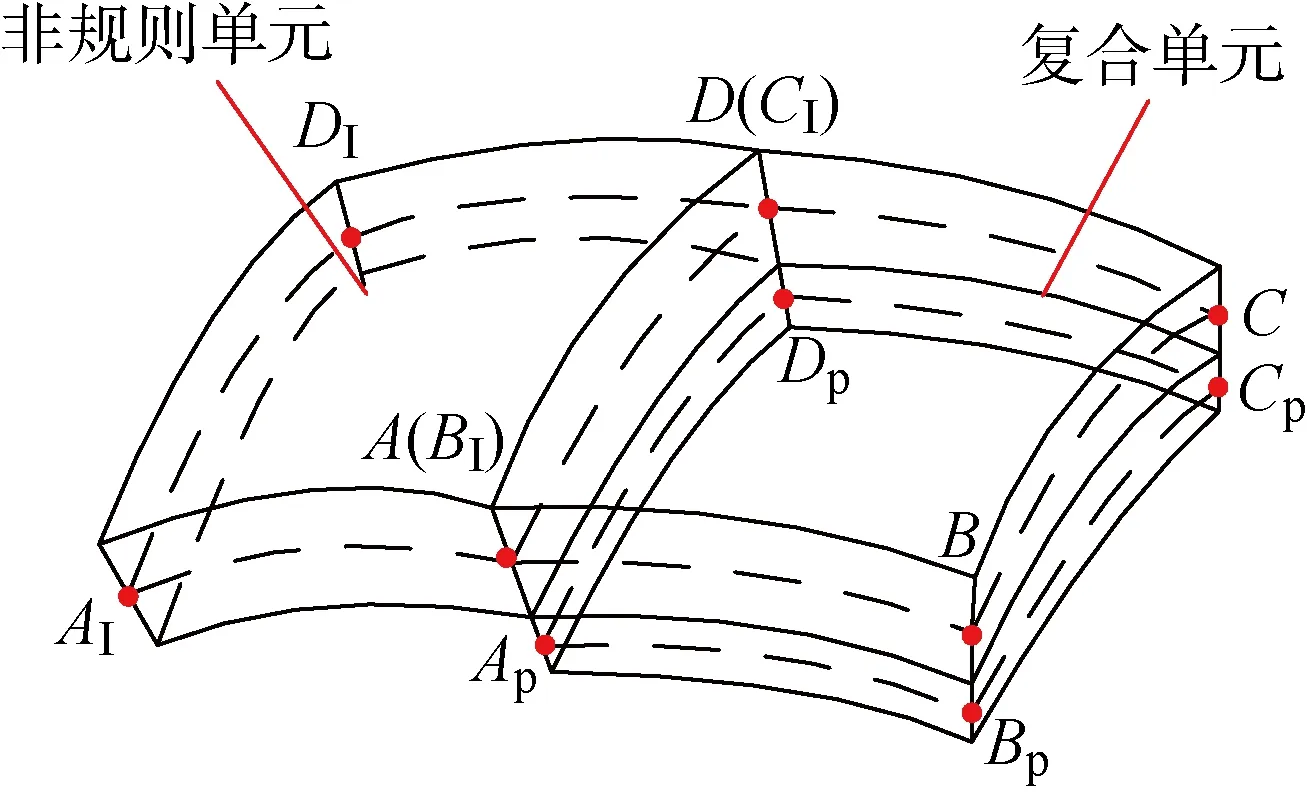
工程中复杂的薄壁曲面结构常由对边不等且各区域厚度不同的非规则大型薄壁加工装配而成.针对非规则的形状特征，为保证模型准确性并减少单元数量，引入高阶插值函数并改进单元形函数，构建边长可独立变化的高阶曲面单元.而采用同一类型的曲面单元离散存在厚度变化的曲面结构时，不同厚度区域单元间的共用节点不在同一中性面上，导致单元间无法使用共同节点进行连接.因此，需要根据厚度分布将非规则大型薄壁结构划分为多个区域进行离散.最小厚度区域使用非规则高阶曲面单元进行离散，而其余区域均使用非规则高阶曲面复合单元进行离散.不同厚度单元间的耦合建模如图1所示，其中(上)下标P表示下层单元.上层单元与最小区域单元的厚度相同，并通过公共节点()和() 连接， 而下层单元节点通过转换矩阵由上层单元表示因此曲面结构变形可以通过最小区域单元节点(～)和复合单元的上层单元节点(～)表示.

2+2+2-1)

纳入标准：（1）均为接受产前检查的孕妇；（2）参与本次研究的孕妇，研究人员应与其讲述本次研究的全部过程，同时孕妇家属应在场，对于本次研究的全部过程清除了解后，孕妇属于自愿参与，并签署知情同意书；（3）孕妇的意识清晰、表达能力优良、精神状况佳；（4）ECGO评分处于0～1分。

1.2 非规则高阶曲面单元模型

基于ANCF，构建非规则高阶曲面单元模型，如图3所示.其中，、和(=1, 2, 3, 4)是可独立变化的单元边长，和分别为变形前后单元上任意一点的广义位置坐标，点为单元上任意一点.单元边长可独立变化且由于引入高阶插值函数，各边均由高阶曲线描述，并能用较少数量单元描述复杂的非规则曲面结构.

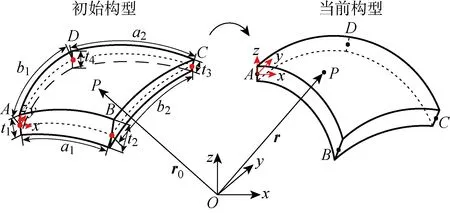
非规则高阶曲面单元的4个节点、、和由位置坐标和斜率坐标两部分组成沿单元厚度方向增加代表二次斜率坐标的高阶项能够减弱泊松锁闭问题并提高数值仿真准确性，因此单元每个节点坐标包含3个位置坐标和12个斜率坐标，单元共有60个节点坐标，定义为

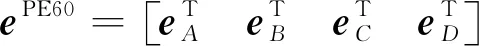
(1)

式中：

另一种方法就是采用子空间跟踪技术[13]。在强干扰环境下，由于接收机接收的GPS有效信号能量很弱，干扰和白噪声占据了接收数据的主能量子空间。而有效信号的检测主要依靠扩频增益，它对消除白噪声的影响很有效，但对强干扰却未必有效，所以接收信号处理的关键是抑制强干扰。基于子空间投影的干扰抑制是一种有效方法，其基本过程是首先找出干扰子空间，再将接收信号投影到干扰子空间的正交子空间当中，投影后的信号即为去除干扰后所求信号，如图2所示。

(2)

=,,,

故单元上任意一点坐标可以表示为形函数矩阵与节点广义坐标的乘积：

通过改善设施结构，不断更新品种，认真执行无公害蔬菜生产技术规程等综合配套技术的推广与应用，大幅度提高保护地生产效益，推动保护地建设的发展，保证农民收入持续稳定提高。

=

(3)

式中：

对非规则大型薄壁结构进行离散，分别得到非规则高阶曲面单元和非规则高阶曲面复合单元的非线性刚度矩阵，复合单元的下层单元节点通过转换矩阵由上层单元表示，进而下层单元刚度矩阵可由上层单元节点求得.利用图1所示的单元间耦合方法，非规则结构的刚度矩阵可由上层单元和单层单元节点推导得到.

[…]

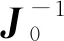
(4)

式中：为60×60的单位矩阵，且

=(2+1)(-1)(2+1)(-1)

=(-1)(2+1)(-1)

=(-1)(2+1)(-1)

=(-1)(-1)

全球金融周期有十年一循环的说法，“逢七见顶，逢八必跌”是近三十年的金融周期新常态，2018年逢八魔咒再度被验证。

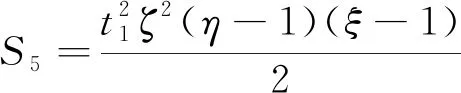
=-(2-3)(2+1)(-1)

=(-1)(2+1)(-1)

=-(2-3)(-1)

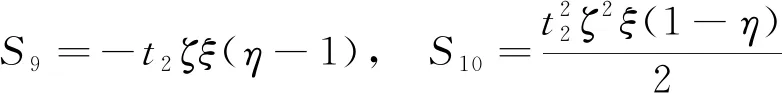
=(2-3)(2-3)

另外，就是要落实农田灌溉工程的运行维护经费补贴。刚才庄先委员提了直补的问题，现在对于到底是直补好，还是补给农田水利的运行管理部门，补他们电费和运行成本，有两种不同的意见。我个人认为，还是补给农田水利的供水单位比较好，这样可以避免水费收取不到位的问题。现在甘肃和南方的一些省，他们的省财政已经对排灌站的电费运行支出和管理支出给予补贴，这样也可以降低农民的水费支出。

=-(-1)(2-3)

=-(-1)(2-3)

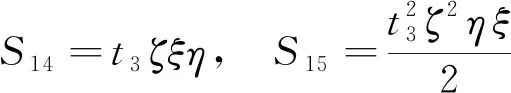
=-(2+1)(-1)(2-3)

=-(-1)(2-3)

=(-1)(2+1)(-1)

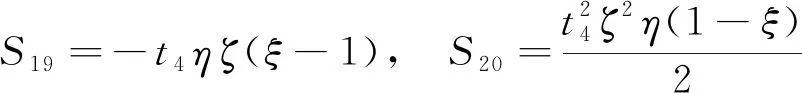
(5)

式中：=、=和=为无量纲变量.

1.3 非规则高阶曲面复合单元模型

基于ANCF，构建非规则高阶曲面复合单元模型，如图4所示.其中，(上)下标M表示上层单元，和为上层单元中性面边长的一半.在上层单元与下层单元间引入高阶斜率约束条件，使得单元间的几何连续性达到连续，消除单元间变形耦合出现的穿透问题，保证复合单元的合理性并提高数值计算精度.

定义下层单元与上层单元接触点分别为和、和、和以及和，交于上层板单元中性面的点′，同理可得点′、′和′

以点和为例，在上层单元与下层单元间的接触点处添加协调变形条件，保证几何连续性.接触点坐标需满足：

(6)

式中：和分别为点和的位置坐标根据式(3)，得到点和的全局坐标：

这幅图事实上很好理解：x1～xn可以看作不同的输入，而w1～wn是这些输入的权重。1则是用于调整的偏置值，一般记为b但可以看作一个输入永远为1的带权值的向量，此时b =w0。Σ是加权的不同输入的和(就是简单的和)，而这一值最终由一个“激活函数”处理，也就是我们说的阀门。整个结构被称为一个“神经元”(感知器)，包含输入部分和输出部分，但从这一点来看，它与普通的数学函数无异。但在一个神经元的内部可以看到，除了输入值不可控和激活函数被预先给定以外，不论是任何一个输入值的权重，以及偏置值都是可以任意更改的，这也是神经元的灵活性之所在。

(7)

(8)

=

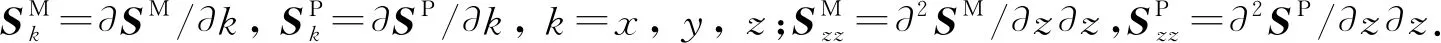
(9)

对于点和、和以及和，同理可得：

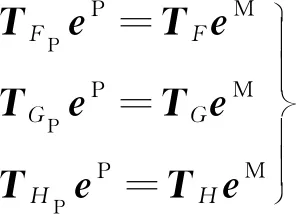
(10)

矩阵形式为

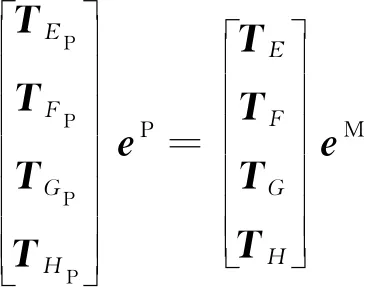
(11)

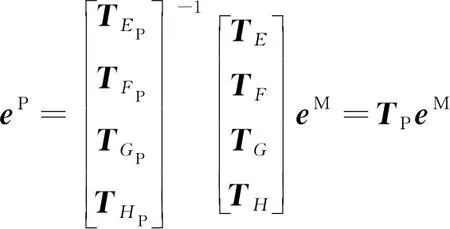
(12)

2 非规则大型薄壁结构装配变形协调模型

2.1 非规则高阶曲面复合单元刚度矩阵

基于非线性连续介质力学理论，推导非规则高阶曲面单元的刚度矩阵.ANCF中的单元计算定义均基于当前构型，单元刚度矩阵随构型变化，因此可以准确描述结构的非线性大变形.定义高阶曲面单元的变形梯度为

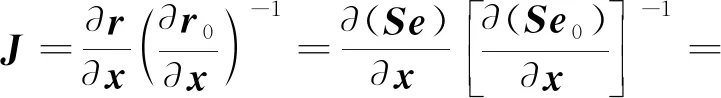
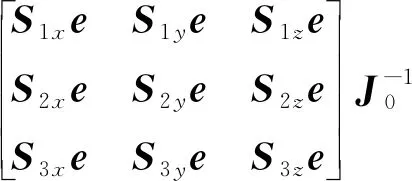
(13)

文献[10]提出了包含风、光、储和电动汽车等的微电网经济调度模型,分析了电动汽车对微电网经济性的影响。文献[11]给出了储能充放电模型。文献[12]以智能住宅内的微电网系统为研究对象,建立了以发用电总成本最小为目标的优化模型。文献[13]建立了电动汽车功率需求的统计模型。文献[14]考虑了电动汽车能量的双向流动,以投资成本最低为目标,同时参与电网的削峰填谷,分析了电动汽车双向充电对电网产生的影响。文献[15]在已有光储电站储能容量配置研究的基础上,针对储能设备选型、光储电站的调度模式、容量配置方法以及光储电站的全寿命周期经济可行性等进行了评价。

(14)

基于相对构型，利用变形梯度推导格林-拉格朗日应变张量为

(+)+(+)+

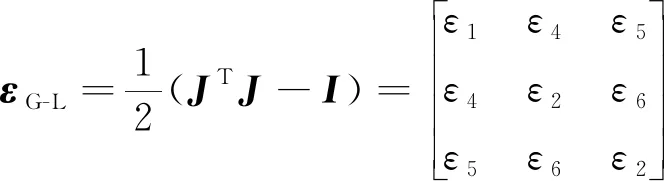
(15)

式中：

红花（Carthamus tinctorius L.）是一种油花两用的经济作物。红花籽含油量为40%左右，其中亚油酸含量为74%～86%，富含维生素A、E和类胡萝卜素等，是一种优质食用油。红花花瓣可作药用，也可提取天然黄、红色素，用于食品着色及配色。同时，红花耐旱、耐寒、耐盐碱、抗病，喜欢阳光充足、气候干燥的条件[7]，河套灌区特别适宜红花的种植。红花生育期一般在120 d左右，一生中采花需要4～5次，费工费力，因此，发展红花产业必须加强基地建设，规模化、机械化是今后的发展方向。

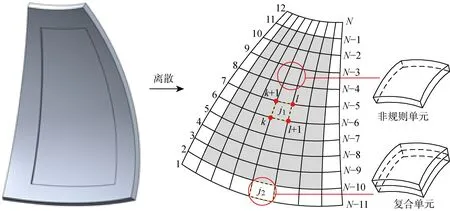
以贮箱箱底瓜瓣结构为例，其离散过程如图2所示.其中，为节点数，为非规则单元，其4个节点编号分别为、+1、和+1，为复合单元.其中间区域与边缘区域的厚度不同，因此分别采用非规则高阶曲面单元与复合单元进行离散.非规则高阶曲面单元和复合单元组合离散非规则大型薄壁结构能够有效解决单层单元无法离散厚度非均匀结构的问题.

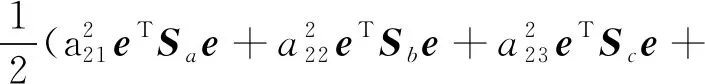
2+2+2-1)

2+2+2-1)

(+)+(+)+

(+))

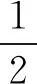
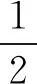
[3]湖南大学岳麓书院文化研究所编：《岳麓书院一千零一十周年纪念文集（第一卷）》，长沙：湖南人民出版社，1986年，第97页。

“让我拍一张菜单，研究上面有什么角色是名存实亡的？”喜欢看侦探卡通的我对儿子说：“应该带放大镜来探索，看看哪样菜色被斩草除根。啊，千万别是你爱吃的肉。”

综上所述，本实验成功构建了LncRNA-GHET1过表达胃癌细胞株 MGC803，为进一步研究 LncRNA-GHET1基因过表达对胃癌细胞增殖、侵袭及转移等行为学的影响奠定重要基础。

(+))

(+)+(+)+

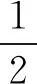
在本地区7家疾病预防控制机构水质检测能力的调查中,常规指标检测能力均达到中级;非常规指标检测能力为低级6家,高级1家;全项指标检测能力为低级6家,高级1家。如表1所示:

如维护服务标的物基本情况、服务人员与服务时间要求、维护服务内容，要求、标准响应时间、服务质量考核制度、数据采集管理、技术咨询及培训服务、指定联系人、联系方式、投标人应在全国范围内具备同类设备维保项目经验、投标人不得转包，分包、外包投标标的主体的要求、所需的服务等。

(+))

(16)

式中：

(17)

应变张量具有对称性，因此应变可表示为包含6个独立应变分量的向量：

(18)

与应变张量对应，选取基于相对构型的应力张量，即第二类皮奥拉-基尔霍夫应力张量()表示曲面单元应力.在弹性变形阶段，与遵循广义胡克定律，因此两者关系为

=||-=:

(19)

式中：为曲面板单元的弹性矩阵，可由拉梅常数和表示为

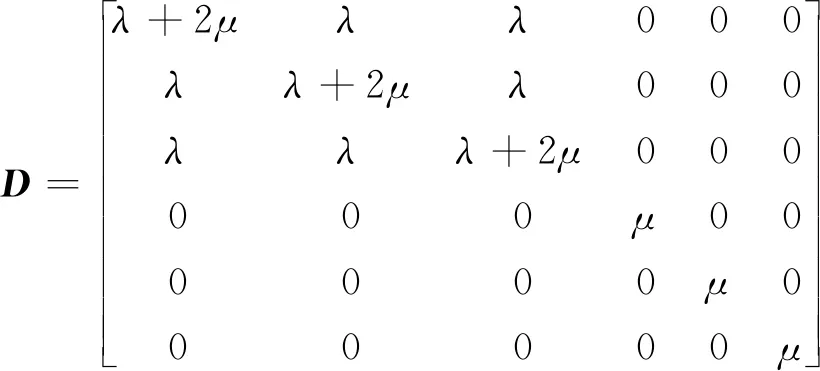
(20)

式中：

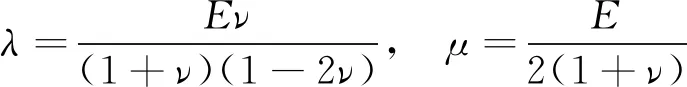
(21)

和分别为材料的弹性模量和泊松比.根据广义胡克定律，曲面单元的弹性应变能为

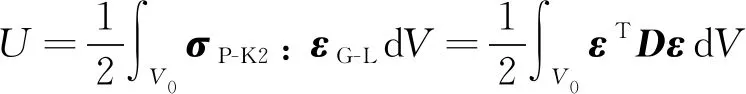
(22)

式中：为初始构型中单元的体积.令式(22)对求偏导，得到单元广义弹性力：

(23)

从而得到与当前构型相关的刚度矩阵：

=(+2)+λ+4μ

(24)

式中：

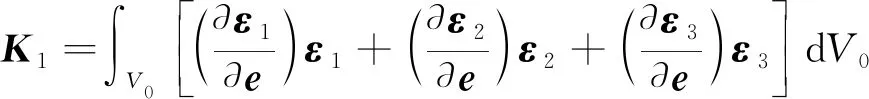
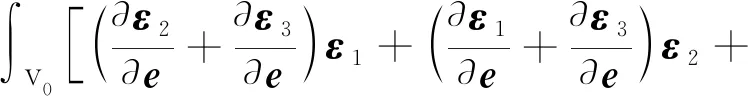
针对构建的非规则高阶曲面复合单元模型，根据式(24)可分别得到上下层单元的刚度矩阵和.结合式(12)，利用转换矩阵将下层单元刚度转换至上层单元局部坐标系内：

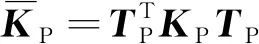
(25)

则非规则高阶曲面复合单元的刚度矩阵表示为

(26)

由式(23)及(24)可知，单元刚度矩阵为节点坐标的函数，与当前构型相关，为非线性的刚度矩阵.因此，利用单元刚度矩阵能够计算非线性大变形.

2.2 非规则大型薄壁结构刚度及广义弹性力

=

典型非规则大型薄壁结构的离散同图2所示.设结构I被划分为个单层单元和个复合单元，单层单元和上层单元共有个节点定义的节点与结构I所有节点之间的对应关系为

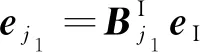
(27)

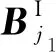
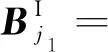
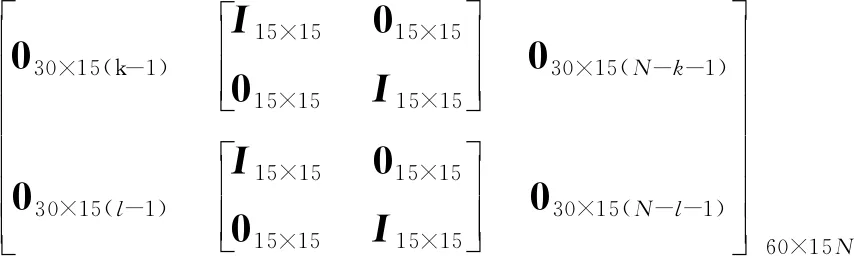
(28)

同理得到的上层单元与结构I所有节点之间的对应关系为

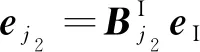
(29)

利用转换矩阵进行刚度组装，得到结构I的刚度矩阵为

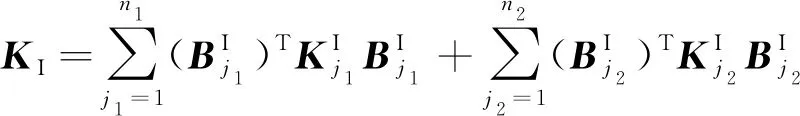
(30)

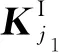
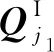
(31)

2.3 非规则大型薄壁结构装配变形协调模型

在装配非规则大型薄壁结构时，一般先利用外加载荷将具有偏差零件的装配区域校正至标准位置后再连接结构，装配结束后释放外加载荷.大型结构具有柔性特征，装配体结构因弹性应变能释放而发生回弹变形.忽略由连接工艺引入的应力影响，假定装配过程中产生的应力均由外加校形载荷作用产生且为弹性力，则取消外力加载后，应力能够完全释放，导致处于标准位置下的装配体发生变形.因此，非规则大型薄壁结构的装配过程可等效为校形回弹过程.计算结构校形到标准零件位置所产生的外力，在装配结束后释放该外力，即可得到非规则大型薄壁结构装配后的结构偏差.

含初始偏差的结构I和结构II的装配过程如图5所示.和′′为装配过程中的约束边，校形力和分别将和′′校形至标准位置.

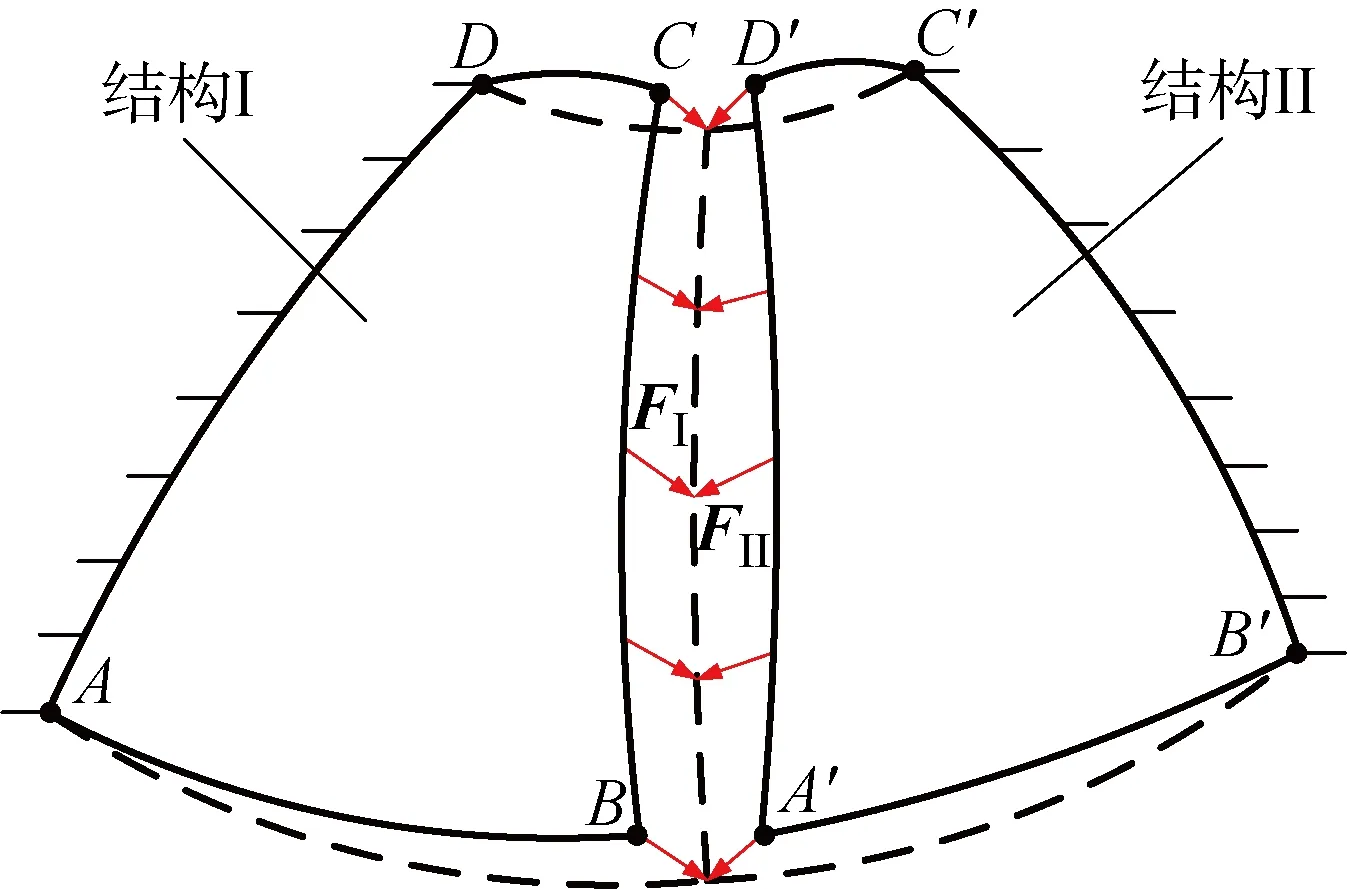
由校形回弹产生的广义弹性力和与相对应的和大小相等、方向相反.校形后，标准装配体结构I-II的刚度矩阵为

(32)

式中：和分别为结构I和结构II相对于结构I-II的坐标变换矩阵，参照式(28)定义.在总回弹力()作用下，标准装配体发生回弹变形，与总校形力大小相等、方向相反.因此，装配过程中的装配体变形协调静力学平衡方程为

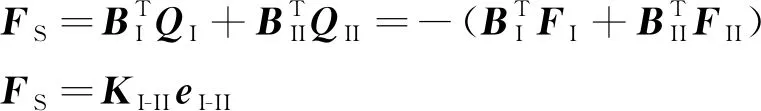
(33)

式中：为装配体结构由标准位置发生回弹后的节点坐标.由式(23)、(24)和(32)可知，为的函数，因此式(33)为非线性方程组.利用数值迭代法求解，根据式(3)并结合单元形函数计算得到非规则大型薄壁结构任意一点的装配后变形.

3 不同厚度分布下瓜瓣结构装配仿真分析

3.1 瓜瓣结构厚度分布及初始偏差定义

基于所提非规则高阶曲面单元及其复合单元构建重型火箭箱底瓜瓣模型，并利用非规则大型薄壁结构装配协调变形计算方法计算装配偏差，分析边缘加厚区域尺寸对瓜瓣装配变形的影响.

重型火箭箱底瓜瓣结构如图6所示.其上下底边分别为直径为900 mm和 9 500 mm的1/12标准圆弧，假设结构最小厚度为18 mm，边缘区域厚度为25 mm，而边缘区域的宽度未知.将上底边加厚区域的宽度定义为从上边线沿母线方向的覆盖长度()，将加厚区域底边所在圆弧对应的圆心角()定义为其沿圆周方向的宽度尺寸，同理定义下底边加厚区域尺寸和.侧边加厚区域的宽度即为母线长度()，而沿圆周方向的宽度尺寸为其底边圆弧所对应的圆心角().

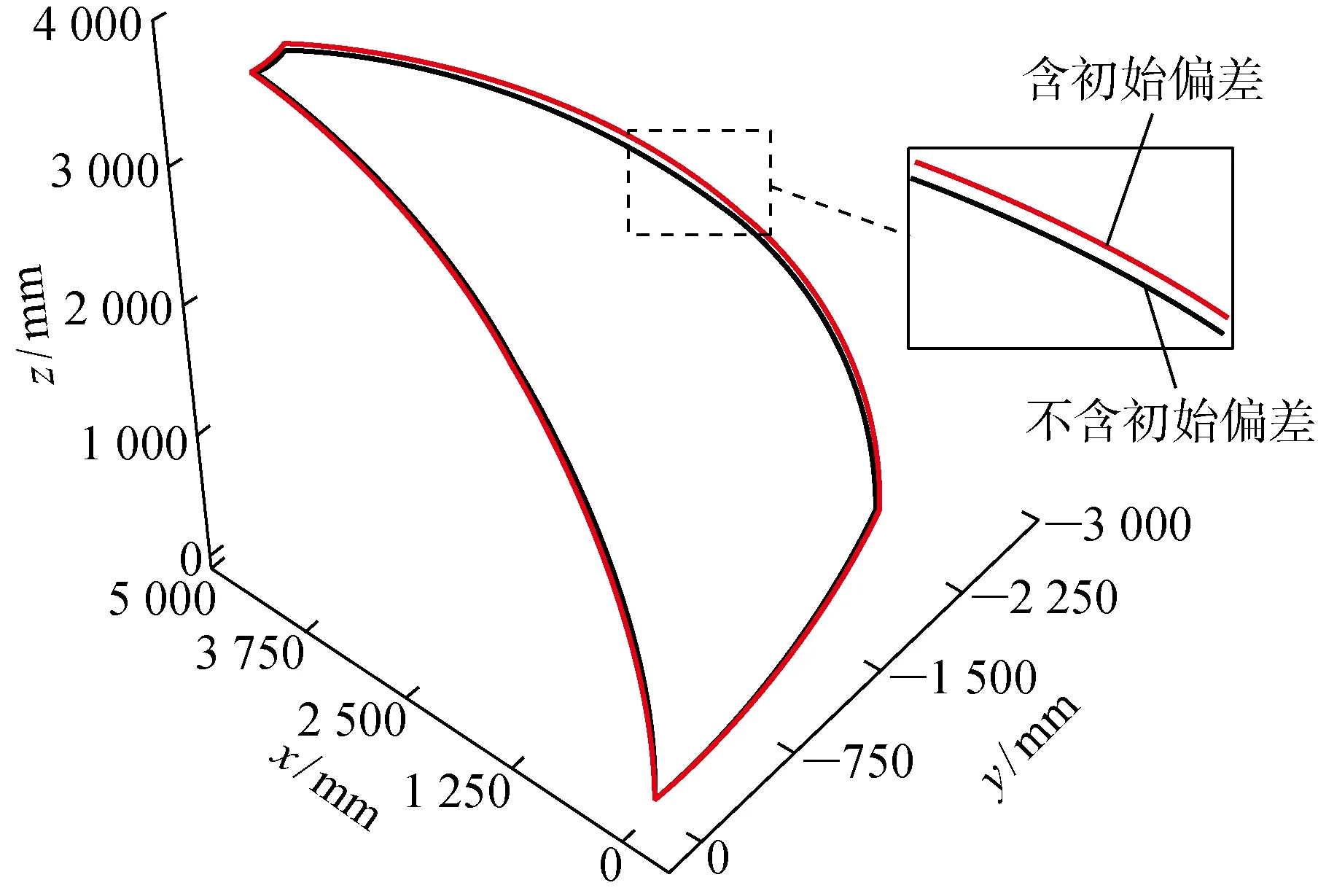
瓜瓣结构的初始偏差主要由加工成形过程的回弹产生.偏差受多因素影响，在一定范围内波动.根据瓜瓣几何型面特征选取关键控制点，按照零件的偏差波动范围得到各点的随机偏差值.利用关键控制点拟合偏差型面得到含有初始偏差的瓜瓣结构，如图7所示.曲面最大偏差为50.2 mm.装配过程参照图5，其中瓜瓣I存在初始偏差，瓜瓣II则为标准结构，两者的厚度分布及尺寸参数相同，可计算装配体的装配变形.

3.2 加厚区域宽度对瓜瓣装配变形影响

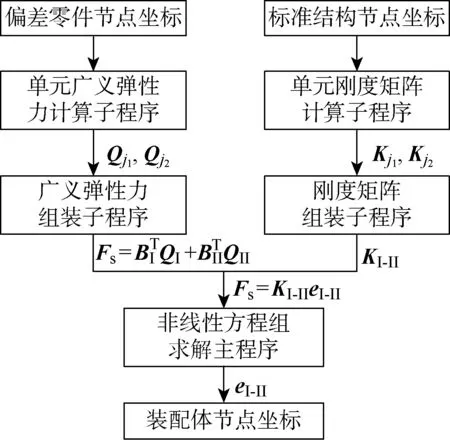
利用MATLAB仿真软件实现所提装配偏差计算模型的数值化，具体过程如图8所示.定义材料为2219铝合金，设=70 GPa，设定密度和泊松比.

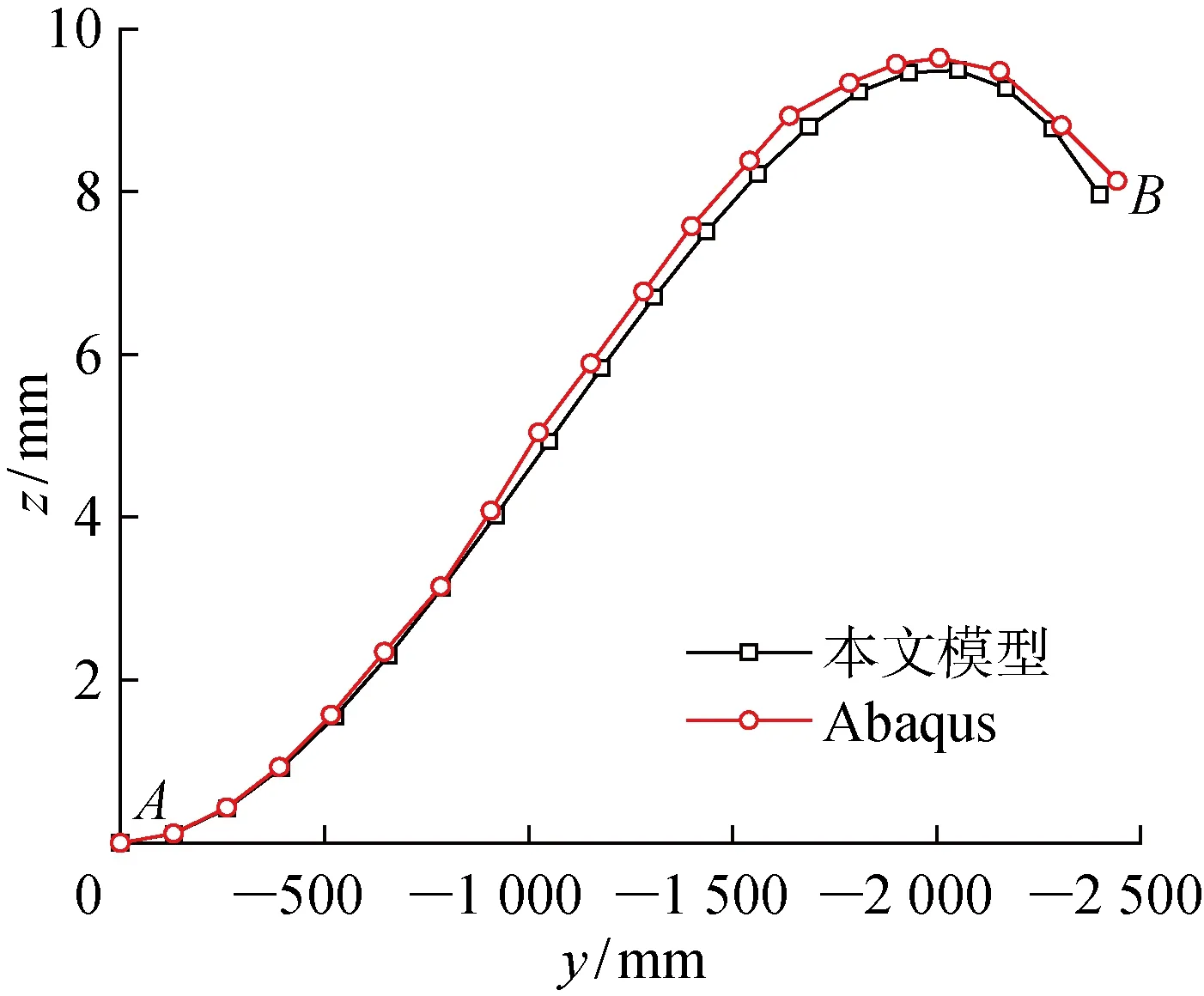
分别利用所提计算模型和Abaqus仿真软件对相同加厚区域尺寸参数的瓜瓣结构进行装配偏差仿真计算，其中，=3°，==250 mm，最大厚度为25 mm.两种方法计算得到的下底边装配后偏差曲线如图9所示.可知，所提装配偏差计算模型结果与Abaqus仿真结果相符，最大误差为3.2%，验证了装配偏差计算模型的准确性.而Abaqus仿真中采用三维实体单元离散结构，为保证计算准确性，模型沿厚度方向至少划分为3层单元.因此，相较于Abaqus的三维实体单元建模，所提方法能以更少单元数量进行建模仿真计算，降低了模型复杂度，同时保证了数值计算准确性.

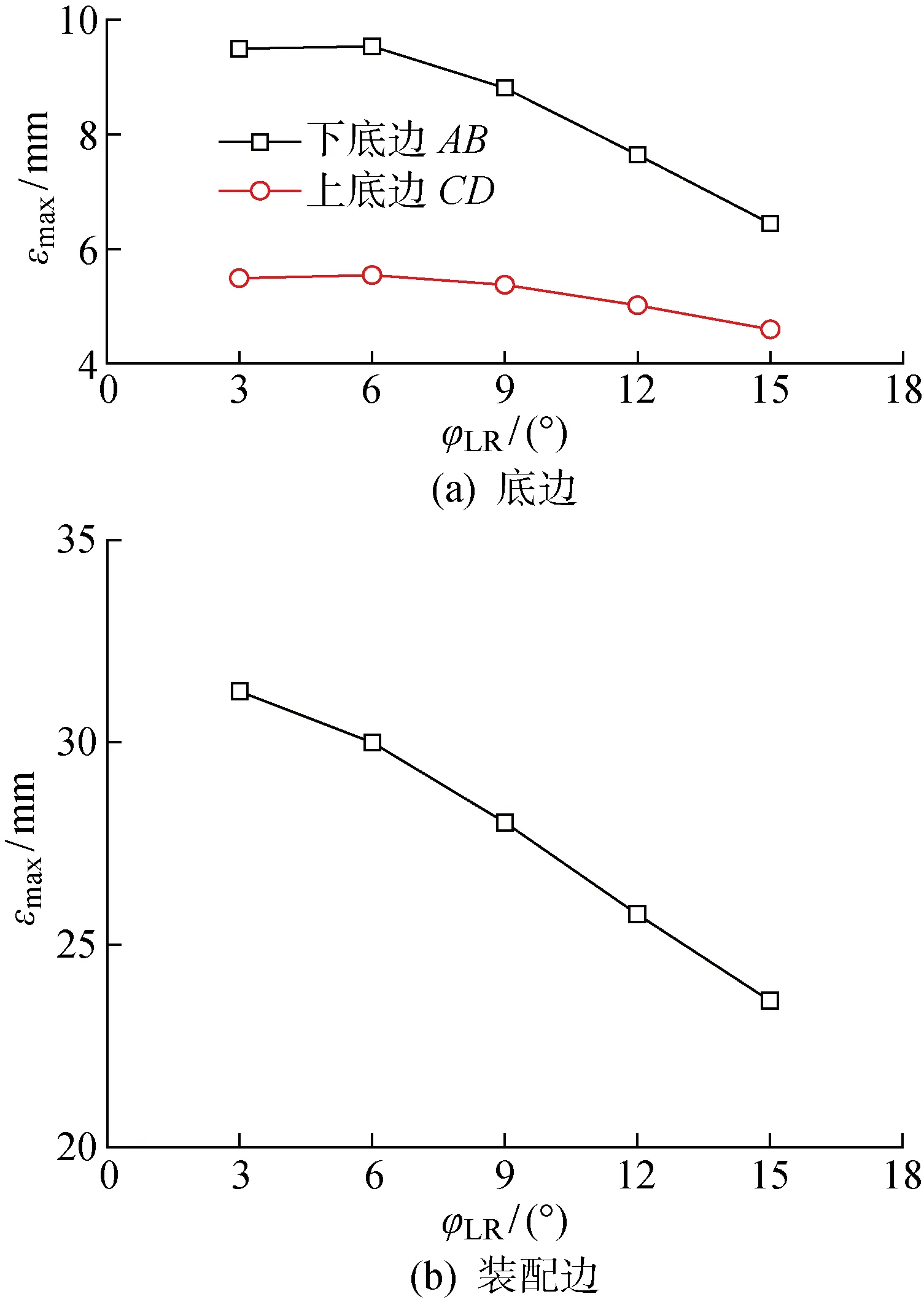
仿真计算不同侧边加厚区域尺寸对装配变形的影响，侧边加厚区域尺寸变化由值表示.图10为不同值对瓜瓣I各边装配偏差的影响.其中，为偏差最大值.可知，随着值变化，瓜瓣结构整体仍近似于大型薄壁结构，装配变形形式受加厚区域参数变化的影响较小；受边缘加厚区域影响，底边装配后最大偏差点出现在靠近装配边端点和处，而装配边装配后的最大偏差点出现在靠近底边端点处.

图11为不同值对瓜瓣I各边值的影响.可知，随着值增大，各边值均呈非线性减小，结构整体刚度增加.而在相同宽度尺寸下，与上底边相比，下底边加厚区域的增加量更大，因此下底边区域的装配变形减少和刚度增大更显著，即径厚比大的区域结构，其刚度受加厚区域宽度变化影响更显著.

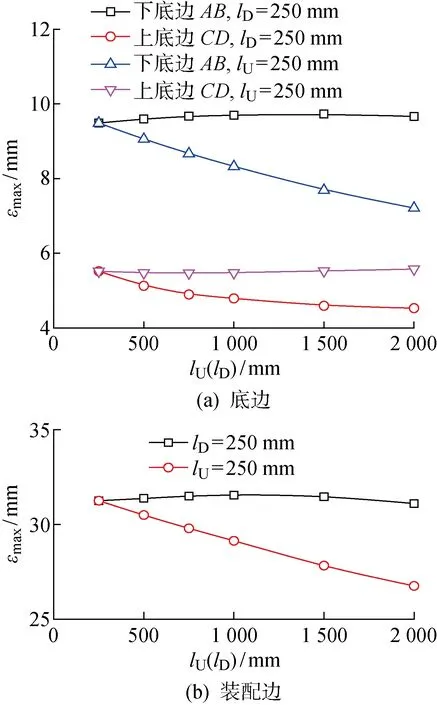
图12为和对瓜瓣I各边值的影响.可知，随着值增大，上底边的值呈非线性减小，而下底边和装配边的值基本保持不变；随着值增大，上底边的值保持不变，而下底边和装配边的值呈非线性减小.底边区域的结构刚度随对应加厚区域宽度增加呈非线性增加，而侧边区域结构刚度随值增大而非线性增加.由于大型薄壁结构的尺寸较大，局部尺寸变化对对应位置的影响显著，而下底边区域比上底边区域的覆盖面积更大，所以对整体的影响更显著.

3.3 加厚区域厚度对瓜瓣装配变形影响

瓜瓣结构的焊接区域厚度对焊后结构的强度影响显著，因此根据焊接区域厚度定义边缘加厚区域厚度.图13为不同最大厚度()对瓜瓣I各边值的影响.可知，随着值增大，上底边和装配边的值呈非线性减小，上底边区域刚度显著增加，厚度增加对局部(径厚比小)区域的刚度影响较大.

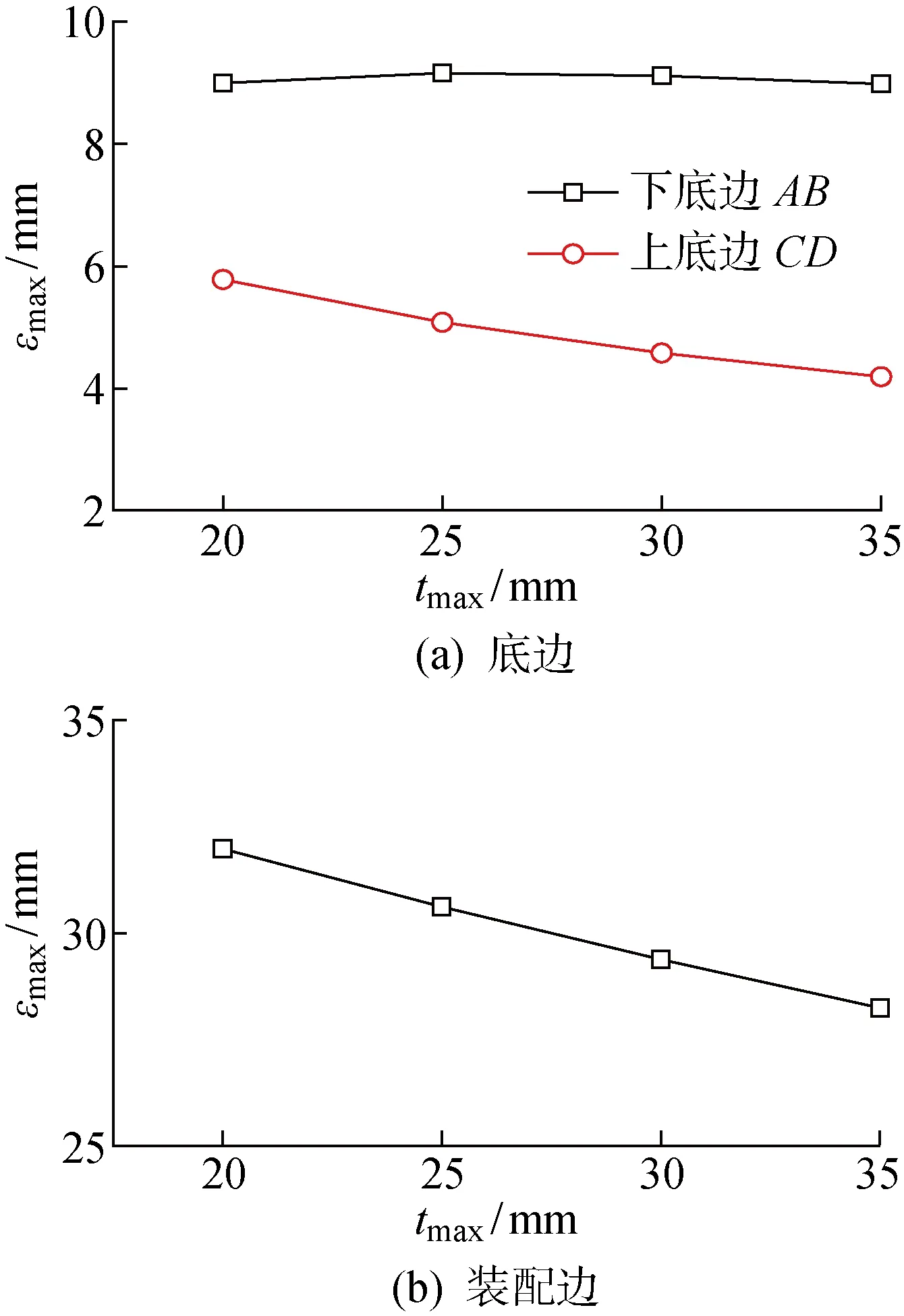
综上可知，在不同加厚区域尺寸参数变化影响下，值均呈非线性变化，且总体趋势为随着加厚区域尺寸增大，值减小，说明装配体整体刚度增加.考虑实际瓜瓣的轻量化设计，保证结构刚度并减少加厚区域体积，选取各结果曲线拐点，即值减小量最小处的尺寸作为结构设计参数.当=250 mm、=500 mm、=25 mm时，随着尺寸增加，刚度变化不显著.随着值增大，整体刚度增加量呈非线性增加，考虑实际轻量化设计及满足焊接区域宽度需求(200 mm)，选取=3°，能够减小装配过程中因整体柔性特征而产生的变形，增加整体结构刚度，减轻后续装配校形难度和工作量，同时满足实际结构设计轻量化需求.

4 结语

基于绝对节点坐标法，提出非规则高阶曲面单元及其复合单元模型；构建不同厚度单元耦合方法，用以离散存在厚度差异且对边不等的非规则大型薄壁曲面结构，有效解决了由单层单元离散曲面结构产生的节点连接问题，以此描述非规则大型薄壁结构的大变形；构建非规则大型薄壁结构装配协调变形模型并解决了装配偏差计算问题.

以重型火箭瓜瓣结构为例，利用构建的变形计算模型对瓜瓣装配偏差进行仿真分析，研究瓜瓣边缘加厚区域尺寸对装配偏差和结构刚度的影响.不同区域的刚度对结构参数变化敏感度不同.径厚比大的区域，其结构刚度受加厚区域宽度变化影响显著；而径厚比小的区域(局部区域)，其结构刚度受加厚区域厚度变化影响显著.根据分析结果提出合理的瓜瓣加厚区域尺寸参数组合，为重型火箭贮箱箱底设计提供指导.