让计算机重新学习加法运算

陈凯

“计算”与其说是计算机的强项，不如说是一个装置之所以被称为计算机的关键能力。人们可以利用计算机实施各类运算，如直接列出表达式做简单的算术题、利用特定算法解方程、通过符号运算推导数学公式等。当计算机强大的计算能力被人们充分利用的时候，它所具有的这种强大能力的一系列缘由却常常被掩盖起来。想象一下，某人在做物理习题时遇见加法运算，在实施运算时，虽然不一定会有意识地回想起自己曾经背诵过“八加六得十四”“八加七得十五”等此类事实，但只要一经提醒，就能明白自己能够完成加法运算的缘由：也许最早的时候不得不依靠摆积木或扳手指的方法，但到后来就能将固定的两个一位十进制数字加法的结果深深刻录在记忆中了，此后，这个深刻的记忆就形成一种运算规律，被灵活地应用到更复杂的加法运算中。再想象一下，若某人用计算机做加法，虽然很容易实施运算并得到结果，但计算机能进行加法运算的缘由，却是隐藏在幕后而不为常人知晓的，并且，也很少有计算机的用户会想到去主动探究。

计算机实施加法的过程与人有很大的不同，有一句流传很广的话这样说：“计算思维是人的思维，不是机器的思维。”仔细揣摩后能够发现，此话其实就已经隐含“机器能思维”的意味在其中，否则也就不至于要对人和机器的思维进行区分了，这颇能引发哲学上的思考：机器能够思维吗？继而还会引发关于怎样才算是机器等问题的讨论，这些不是本篇文章讨论的重点，笔者想请大家关注的是“计算思维是人的思维”这半句话中并没有明示出来的问题：计算思维到底是人的怎样的一种思维？既然这种思维不是机器的思维，它又是如何和机器发生关联的？——否则该论断也就不需要和所谓机器的思维做对比了。笔者希望能通过一些简单的用机器实现加法的例子，来逐步揭示问题的答案。

● 实现二进制加法的全加器电路

先来看一个十分常见的全加器的逻辑电路，它通常被称为全加器（如图1）。这个装置可以接受三個仅有一位的二进制数的输入，然后经过一系列的逻辑运算，得到两位的二进制输出值。如果三个输入中只有一个“1”，那么结果中高位是0，低位是1;如果三个输入中有两个“1”，那么结果中高位是1，低位是0;如果三个输入都是“1”，则结果的高位和低位都是1。

若是根据逻辑电路图，逐个跟踪各个逻辑元件输入和输出信号的变化，便可知这样一个电路的确能实现三个一位二进制数的加法的运算，然而并不能解答这样的疑惑：为什么它能够起作用？尽管整幅电路图如此清晰而直观地呈现在人们面前，但大部分人仍然很难通过观看这张电路图，就领悟机器的计算需要如此结构的原因。

即便是将电路图转化为逻辑表达式，如高位的输出值和三个输入值的关系为h=（a^b）&c|（a&b），虽然可以借由a、b、c值的输入和逻辑计算，看出这个表达式的确能实现加法运算后二进制高位的输出，同样很难看出，何以这个逻辑表达式能起作用。对于逻辑电路图也好，逻辑表达式也好，大部分人都能很轻松地经由推演和逐步跟踪的方式验证它的正确性，却很难在整体上领悟（很难，但并非不可以，笔者将在后续文章给出一种启发领悟的方法）它为何能够以这样的结构来运行。换言之，很难领悟这种能够正常工作的系统结构到底是怎么被设计出来的，一个简单的二进制加法装置尚且存在这样的困惑，更何况那些复杂很多的计算系统了。

● 重新推理出二进制加法逻辑电路

假设学生已经掌握了基本的逻辑运算，那么想要解释清楚怎样实现二进制加法运算，并不是非常困难的事，这个观点似乎和上面的事实有很大的矛盾，但由于计算方式是多样的，所以的确存在更容易理解的二进制加法电路。下面来说明一下。

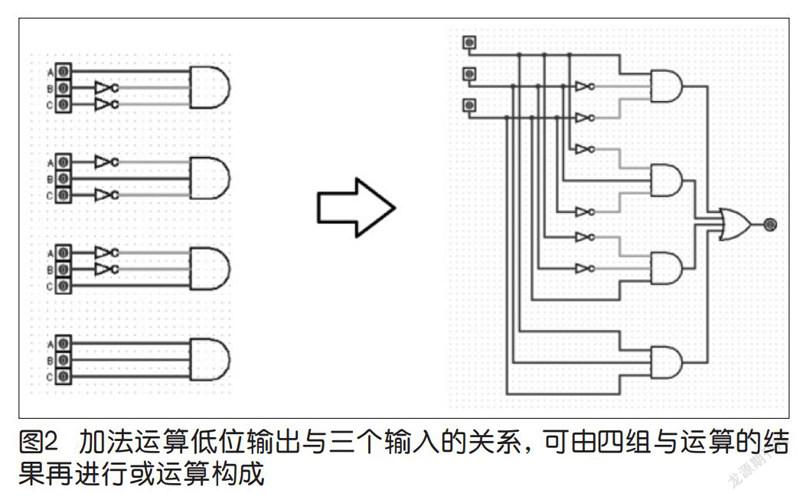
经由简单的逻辑推理可知，只有当a、b、c三个输入中仅有一个是1，或者全部是1的情况下，加法装置的低位才是1，否则是0。可以将这个逻辑判断过程用逻辑电路的方式来表达，从中可以看出一个大的部件是怎样由四组小的部件拼接起来的，绘制出来的图颇有一种规律性的美感，如图2所示。

另外，当a、b、c三个输入中有两个或三个1时，加法装置的高位是1，否则是0。也可以用逻辑电路以很有规律的方式表达出来。如图3所示。

笔者特意将图2元器件方向和图3元器件的方向设得不同，这样，就可以将两张有规律的图轻松合并在一起，组装成一张更大的图，然后就能实现二进制的加法了（如下页图4）。

这个加法器的逻辑电路图看上去颇有一种能够治愈强迫症的感觉，而且很容易用人的思维来理解它何以能够工作。它总共有19个逻辑元件，考虑到逻辑电路图中的逻辑门支持了多个输入，若是仅使用两输入的逻辑门，那么这个加法器实际上要用到31个逻辑元件。相对来说，图1所示的全加器电路只有5个元件。要是从“何以如此结构能够正常工作”的角度来发问，图1的全加器反而更让人难以理解。不过图1的全加器电路有其自身的优势，其中一方面的优势是显而易见的：因为结构简单，所以制作成本低，稳定性也高。其实还有另一方面的优势，在复杂的电路中，图1的全加器更容易实现封装和模块化，限于篇幅暂不展开。很显然，可以发现其中的矛盾：人容易理解的结构不是被实际广泛应用的结构。

● 机器的思维和人的思维

现在重新回到关于“人的思维”和“机器的思维”的讨论。有一个很著名的思想实验这样说：如果把一个钟的零件拆散，放进一个盒子反复摇动，那么只要时间足够久，而且零件也足够牢靠，最终盒子里的零件会自动组装成一个完整的钟。也可以反过来考虑，当人们打开一个盒子，发现里面是一个完整的钟，那么人的头脑认为更可能的情况，究竟这个钟是来自非常长的时间的摇晃而自动组装成功的，还是由人手工组装成功的？显然，前者可能性是极其微小的。可以试着做一个简单的调查，用常规的5个逻辑元件的加法器和笔者提供的29个元件的加法器作对比，问学生哪一个结构更可能是人工设计的，得到的答案更多的是后者，虽然实际上，人们在真正设计和制作电路时，却几乎总是使用前者的结构。如果换一种问法，问两种结构的机器，哪一种更可能是在盒子里摇晃而成的，那么得到的答案就明显倾向于前者。这让笔者忽然领悟到，相对于“人的思维”和“机器的思维”的区别的问题，更值得思考的，是“更像人的思维的机器的思维”和“不像人的思维的机器的思维”两者的区别。

这里给出另一个非逻辑电路的例子。图5是元胞自动机“生命游戏”中的一种图案，名称叫“滑翔机”。“生命游戏”的变化规则非常简单（相关变化规则可以方便地在网络上查阅到，这里不再说明），元胞自动机中的每一个格子的变化，都很容易根据预设的规则推演出来，但哪怕如图5左上角那样只有五个亮点组成的图案，人的头脑也很难凭空想象出这个图案在后续变化中会陷入周期性的重复模式，并在整体上仿佛滑翔机一样逐步漂移到原来位置的右下角。这个“滑翔机”图案还具有传递信息的作用，以至于可用于在“生命游戏”中构建起加法运算装置，图6是这个加法运算装置的局部（完整结构所占篇幅太大，这里就不展示了），尽管它在运行过程中的每一步都能依靠人的思维来跟踪，但除非是这个装置的创建者，其他人在看到这个装置时，仅仅能看出局部的图案具有某些规律性，在更长久的时间上，难以把握住图案的整体变化，也几乎无法判定结构中每个部件的作用、部件之间的关系以及整体的工作原理。

从全加器的例子到元胞自动机“生命游戏”的例子，可以看出人的思维的局限，人很容易接受简单的规则，然后用这个简单的规则构建起一个自动化工作的系统。但人在面对一个复杂的需求的时候，头脑仍然希望这个构建过程是具有某种规律性的，并希望每一個局部的构造动作都存在着目的。正是在这一点上，人的思维和非人类的“思维”产生出了重要的区别，一个自然的机器——假设把自然中的事物按规律运行视作某种机器的话——它的构建是生成性的，系统中的局部的结构并不存在目的性，而是在宏观的混沌的运行中涌现出了某种意义，这些并非以人惯常的思维运作的机器并不会产生出需要人去理解它的意愿。

然而，高效简洁的全加器恰恰是由人自己设计出来的;局部极其简单，整体却复杂混沌的“生命游戏”的加法装置也是由人自己设计出来的;更具有普遍性的例子是，虽然计算机底层的机器指令极其复杂，难以让人理解，但人却能够借助更接近人的思维的高级语言代码来实现复杂的计算。所以就必须追问一个问题：为什么人有这样的能力？

至少在当前，人并不按机器思维的方式来思维——这里暂不讨论在头脑中植入计算机的未来场景。但是人却有一种自由。选择A：构建一个按人惯常的思维方式来工作的机器;选择B：构建一个并不按人惯常的思维方式来工作的机器。于是人们发现这样的问题，人往往需要先选择B，然后才有可能选择A，并且越是在机器的底层，按B方式的思路越是容易构建出现实中真正的可用于计算的器物。计算思维不是这种器物的思维，而是构建这种器物的思维。所以，笔者这样来理解“计算思维是一种人的思维”，这种人的思维可以更具体地认为是一种“能够将机器按机器的思维模拟出某种人的思维”的人的思维。