基于加权动态规划算法的道路交通信号灯配时方案研究
2022-06-06廖菲菲贺春林陈毅红
廖菲菲,贺春林,陈毅红
(西华师范大学 a.计算机学院,b.物联网感知与大数据分析南充市重点实验室,四川 南充 637009)
随着经济的快速发展和汽车产业的日趋成熟,我国机动车人均保有量呈现大幅度上升的趋势。机动车给人们的出行带来方便的同时,也给城市交通增加了压力,大中型城市交通拥堵现象越来越严重。交通拥堵不仅增加了尾气的排放,还可能对参与交通的非机动车及行人安全造成影响。城市交叉路口交通信号灯在交通行为中扮演了重要的角色,合理有效的配时方案能有效缓解交通压力和预防拥堵[1]。城市道路建设决定了该路段的通行能力,但对于车流汇聚的交叉路口,交通信号灯的合理设置除了保障交通参与者的安全以外,还能保障路段的通行能力得到有效的发挥。
由于车流量的变化无法精准计算,因此当前对交通信号配时方案的研究重点主要是以分级的城市道路交叉口为基础的模糊控制方法以及两级模糊控制方法等非线性优化模型[2-4]。通过对车流量的预测和对平均延误时间的计算来实时调整配时,在交通流量具备一定规律的情况下,预测数据有比较好的指导意义,但面对如交通事故、道路破损、车道变化等非规律性事件时,预测数据无法做出准确判断,因此模糊控制方法在面对规律分布的车流时有较好的效果,但对非规律分布的车流情况下的拥堵改善提升有限。下面将提出一种利用动态规划算法,建立交叉路口车流动态规划模型,利用传感设备计算路段车辆饱和度,通过设置的阈值对信号灯周期实时调整。与非线性优化算法相比,动态规划模型可以通过采集实时交通流量进行配时调整,能很好地应对各种突发情况,适用性较非线性优化算法更强。
1 交通概念说明
1.1 信号相位
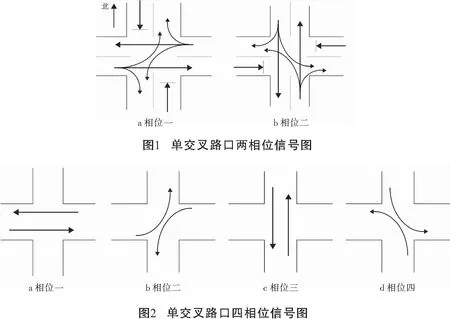
在我国现有交通通行原则下,一般道路均允许全时段右转,即右转绿灯常亮或无右转向灯。因此在单交叉路口中,信号相位一般分为两相位和四相位[5]两种,对应路口模型如下图1、图2所示。
图1所示为两相位信号,相位一为东西向允许直行和左转,南北向禁止直行和左转;相位二为南北向允许直行和左转,东西向禁止直行和左转。图2所示为四相位信号,相位一为东西向允许直行;相位二为东西向允许左转弯;相位三为南北允许直行;相位四为南北向允许左转弯。
两种相位信号的差别在于:两相位直行与左转同时进行,适用于车流量小且道路车道数少的情况;四相位直行与左转分离,因此车道数不少于3道,适用于车流量较大的情况。
1.2 时间参数
1.2.1 信号周期
信号周期(S)指同一相位下从绿灯开始到红灯结束这段时间的总和。S=Tg+Tr+Ty。式中,Tg表示绿灯持续时间,Tr表示红灯持续时间,Ty表示黄灯持续时间。根据不同相位及流量,一般信号周期设置为60~180 s[6]。
1.2.2 有效绿灯时间
实际情况下,从绿灯亮起至第一辆排队车辆通过停止线,通常需要一定时间,包括司机反应时间、车辆启动时间、车辆行驶时间等,该时间称为前损失时间。而在绿灯即将结束前一般会设置绿灯闪烁时间,用于提醒即将通过停止线的车辆减速停车,此时间称为后损失时间。绿灯持续时间减去前后损失时间即为有效绿灯时间(Teg),即允许车辆通过路口的时间。
1.2.3 等待时间

2 基于动态规划算法的交通信号灯配时模型
现有信号灯配时方案具备以下几个特性:(1)周期固定性:信号配时严格按照制定好的策略周期性变化,如:红-绿-红;红-绿-黄-红;红-黄-绿-黄-红等;(2)配时固定性:现有配时方案中,对信号灯变化时间间隔均为固定时间,如遇严重拥堵,可能需要交通警察现场手动操作信号灯;(3)相位固定性:十字路口通常分为4个固定相位,交通流向及规则均固定不变。
固定特征有助于交通参与者对下一时段的相位变化规律有较好的预测,但是由于交通流量的不确定性,因此固定特征对交通拥堵时车流量的迅速疏通不利。以下将建立基于动态规划算法的交通信号灯配时模型,旨在缓解交通拥堵情况。
2.1 阈值设置
由于车流的实时变化,很难用精确数据确定当前各个车道通行或待行车辆数,因此路口等待时间及平均等待时间也无法计算。此处可以使用阈值来近似判断待行车辆数,以一辆车车长5米、两车间隔1米计算:n辆车排队等待时,待行路段约6n米,利用压力传感器或光线传感器作为触发器,可设置为第一阈值;同理12n米为第二阈值,18n米为第三阈值。当第一阈值未触发时,认为该车道车流正常无拥堵,第二阈值触发为轻度拥堵,第三阈值触发为严重拥堵。
2.2 权值设置
为缓解拥堵,引入车道权重参数,该参数影响车道放行优先级。当车流稀疏时,所有路段权值相同,信号配时按初始方案执行;当某一车道产生轻度拥堵,则提升该车道优先级,按权重比例增加该相位绿灯补偿时间;若优先级超过设置阈值,即该车道严重拥堵时,可提升该车道放行频率,最大通行能力放行,以缓解拥堵。
2.3 延误模型
车辆排队延误时间由两个部分组成,第一部分为上一个绿灯周期未通过的车辆数与等待时间的乘积,第二部分为红灯周期新增车辆数与等待时间乘积。


一个完整信号周期内红灯时间r秒内和绿灯时间g秒内的平均车辆延误为:
车辆平均延误和总延误时间是交通信号灯配时的关键参数之一,决定了交通路口的通行能力和拥堵程度,是交通信号配时方案的最主要的评价指标。
2.4 评价指标
2.4.1 有效通行能力
从一个相位绿灯亮起到第一辆车通过路口所需时间为前损失时间T1。绿灯即将结束时车辆一般会提前减速等待,此段时间为后损失时间T2[7]。一个绿灯周期内该相位的有效通行能力为:
Q=f(v)·Teg=f(v)·(Tg-T1-T2)。
式中,f(v)表示该相位车流的速度函数。
2.4.2 饱和度
一个绿灯周期内通过路口的车辆数(q)与该相位最大有效通行能力(Q)的比值即为该相位的饱和度:γ=q/Q。饱和度是道路通行状态的评价指标,反映了该相位的交通负荷,当其数值范围为[0,100%]时,即说明在一个绿灯周期内,路口等待车辆均可通过路口;当其值大于100%时,说明等待车辆需等待多个绿灯,即发生拥堵。饱和度与交通流量、通信效率、发生拥堵概率成正比,可借助道路传感设备通过设置阈值来量化。
2.4.3 平均等待时间
交叉路口所有车辆从进入路口等待到通过路口花费的时间和与车辆数之间的比值,是评价交叉路口交通流量状态的重要指标,同时也是评价配时方案合理程度的关键指标[8]。
2.5 动态规划算法
动态规划算法是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决的一种算法思想。基于动态规划的信号灯配时模型对算法的决策部分进行应用,以相位饱和度为参数对该相位绿灯时间进行动态调整。为保障道路的通行能力和通行效率,一般控制饱和度在80%左右[9-10]。在本模型中,设置饱和度的最佳范围为[70%,90%],决策计算公式如下:
(1)
当饱和度不在最佳范围时,对Teg以常数c进行增减,确保相位处于最佳饱和度即最佳通行状态。常数c为整数,且取值范围为1到最小绿灯周期之间。
本模型的算法流程如下:
Step1 问题分解:将问题分解为4个子问题,4个相位分别计算;
Step2 确定4个相位的相互影响关系:4个相位绿灯周期切换次序依次为1-2-3-4;相位一与相位三的红绿灯周期相反,相位二与相位四的红绿灯周期相反;
Step3 根据决策计算公式分别计算各相位的红绿灯周期及切换时间,确定初始状态;
Step4 实时监测路口交通拥堵情况,一旦触发阈值控制器,则转至step3;
Step5 相位决策循环执行。
3 模拟实验

表1 模拟交叉路口信号周期
实验选取VISSIM智能交通仿真平台,版本为14.3。首先在VISSIM中建立一个双向六车道的十字交叉路口模型,并设置全时段允许车辆右转,即形成四相位交叉路口。
3.1 实验参数设置
初始状态下,该交叉路口的信号周期如表1所示。初始周期设置对本模拟实验结果无影响,随机设置周期时间为123 s。
3.2 模拟交通流量
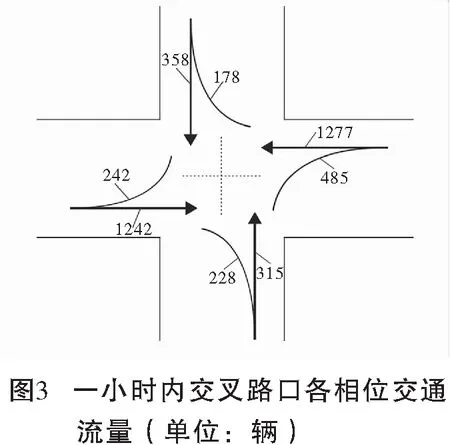
交叉路口车流量数据采集地点为某某市某十字路口,观测时间为2021年3月26日星期二上午7∶30—8∶30,该时段内路口交通流量如图3所示。
根据决策计算公式(1)对初始信号进行调整,常数c的取值选择从1 s到8 s,经过模拟实验,可知c的取值对算法的性能影响如图4所示。当c的取值增加时,平均等待时间也呈递增趋势,证明c值越大,算法的性能越差;但当c值递增时,算法的收敛速度提高。根据图4结果,在保证算法性能的同时尽可能使得收敛速度满足实时需要,选取c=3进行模拟。运行动态规划算法模型后,经8轮迭代后趋于收敛,迭代过程如表2所示。
表2中,经过对相位饱和度的计算确定优先级,对饱和度不在最佳范围的相位给予增加或减少绿灯补偿时间,以达到减少周期时长、提高通行能力、减少平均等待时间和平均延误时间的目的。表3为7∶30—8∶00的14个周期内,三种不同配时方案的平均等待时间表(与定时配时方案及基于GA的模糊控制优化算法[10]相比)。固定配时方案由于无法有效调整绿灯时间,导致相位三每个周期都有剩余车辆无法通过路口,持续积压后形成拥堵,平均等待时间不断增加;基于GA的模糊控制优化算法于第7周期收敛,最优值为65.04 s;基于动态规划的配时方案于第9周期收敛,最优值为60.58 s。实验证明,动态配时模型在收敛后,与固定配时相比,能减少68.97%的平均等待时间;与基于GA的模糊控制优化算法相比,在收敛速度上慢2个周期,但能有效减少6.86%的平均等待时间,对缓解交叉路口交通拥堵情况有较好的效果。
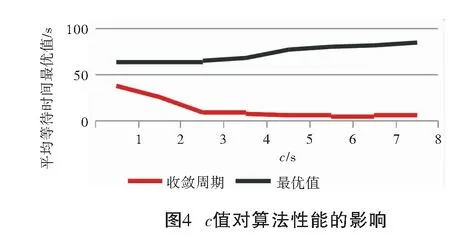

表2 动态配时模型信号周期
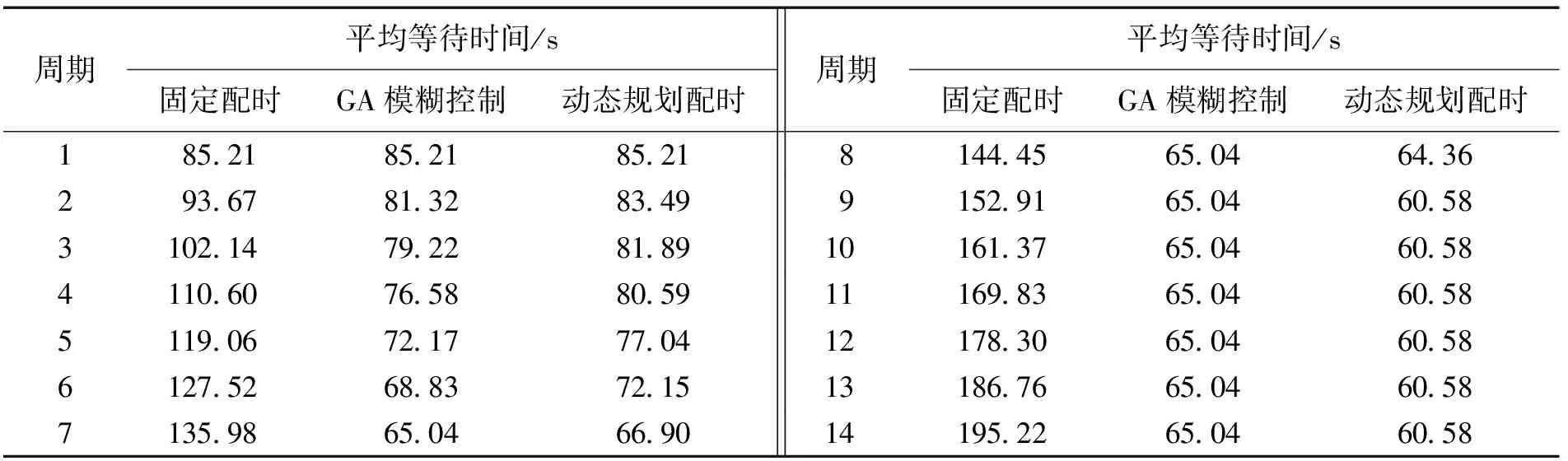
表3 三种算法平均等待时间
4 小结
基于动态规划的配时方案通过对道路交通流量的监控,根据饱和度确定相位的优先级,实时调整下一周期的信号灯绿灯周期,在模拟实验中能有效地预防拥堵现象,并对已发生的拥堵状况有明显的改善作用,具备一定的理论和现实意义。
通过模拟实验可知,虽然动态规划的配时算法有一定的效果,但收敛速度仍不够优秀,且最优值也并非最好,还有继续改进的空间。在今后的研究中,可以尝试对常数c的取值进行动态调整,可能会取得更优的算法。
