串并联系统中休止时间的随机比较
2022-06-06罗天奇
罗天奇
(兰州石化职业技术大学,兰州 730070)
将元件分配给串联系统中的元件是一种常见的方法,被广泛应用于提高系统的可靠性。在实际情况中,通常遇到两类基本系统:由旧元件组成的系统和旧的系统。过去几十年,系统热冗余分配问题被许多作者研究。Boland等[1-2]应用几种随机序研究串并联系统的这一问题,并取得了一些奠基性成果。后来,Singh和Misra[3]沿这一方向继续研究。最近,Valdés和Zequeira[4-5],Yan和Luo[6]进一步丰富了现有成果(其它更多的相关研究可参考文献[7-9])。前面的作者只考虑串联系统冗余分配问题,而我们考虑将旧元件分配到旧系统与新元件分配给新系统的休止时间问题以及由两个元件组成的串联系统的休止时间问题,也就是旧元件分配到旧系统系统失效所需的时间与新元件分配给新系统系统失效所需的时间哪个更长。
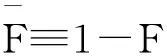
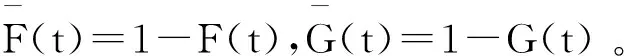
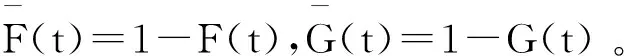

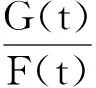

上面几种随机序之间有如下的蕴含关系:X≤hrY⟹X≤stY,X≤rhY⟹X≤stY。关于随机序更加详细的讨论请参阅参考文献[10]。Ruiz和Navarro[11]定义了由条件随机变量Xt=(t-X|X≤t)定义的休止时间(IT),表明了在元件寿命小于或等于t的情况下,失效所需的时间,随机变量Xt也可称为反向剩余寿命(或失效后的时间)。
具有寿命t≥0元件的休止时间表示为X(t)=(t-X|X≤t),旧元件组成的串联系统min(X(t),Y(t))、并联系统max(X(t),Y(t))、旧系统(min(X,Y))(t)、(max(X,Y))(t)。Li和Lu[12]证明X和Y同分布,min(X(t),Y(t))≤st(min(X,Y))(t),max(X(t),Y(t))≤hr(max(X,Y))(t)。Yan和Luo[6]证明X和Y不同分布max(X(t),Y(t))≥hr(max(X,Y))(t)。本文基于Yan和Luo[6]的工作,进一步研究冗余系统min(max(X(t),Z(t)),Y(t)),(min(max(X,Z),Y))(t)以及max(X(t),Y(t))≥rh(max(X,Y))(t),max(X(t),Y(t))≥lr(max(X,Y))(t)随机率序下的的随机比较问题。
1 一个元件分配到两个元件组成的串联系统组成串并联的休止时间
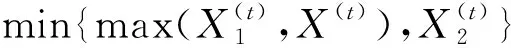
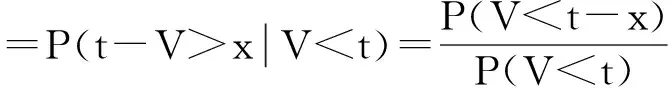
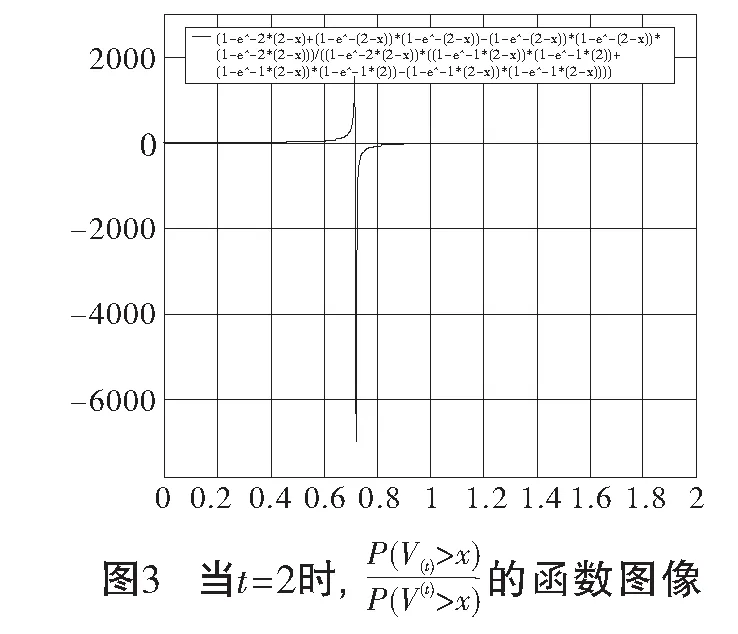
下面的例子显示在普通随机序下并不能得到V(t)≤V(t)或V(t)≥V(t)。


特别地,x=0.05时,P(V(t)>x)=0.998 447 595,P(V(t)>x)=1.004 387 475,即V(t)≤stV(t);x=0.15时,P(V(t)>x)=0.995 449 221,P(V(t)>x)=0.983 009 65,即V(t)≥stV(t)。


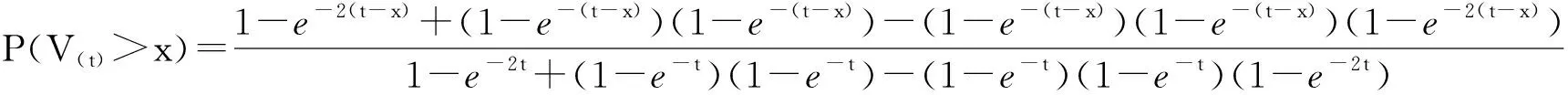
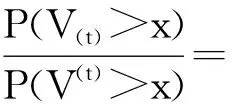

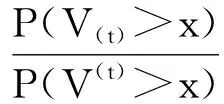

接下来的定理显示在一定条件下V(t)与V(t)可以随机比较。
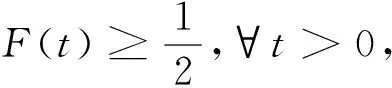
证明V(t)和V(t)的生存函数分别为

设g(x)=F(t)-F(t-x)+2F(t-x)[F(t)]2-F(t)F(t-x)=F(t)-F(t-x)(2F(t)+1)(1-F(t)),
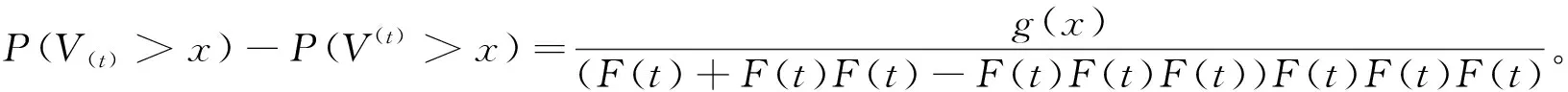
g′(x)=f(t-x)(2F(t)+1)(1-F(t))≥0,
gmin(x)=g(0)=F(t)-F(t)(2F(t)+1)(1-F(t))=F2(t)(2F(t)-1),

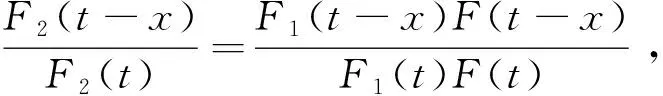
证明V(t)和V(t)的生存函数分别为

要证明V(t)≥stV(t),只需证明P(V(t)>x)≥P(V(t)>x),
P(V(t)>x)-P(V(t)>x)
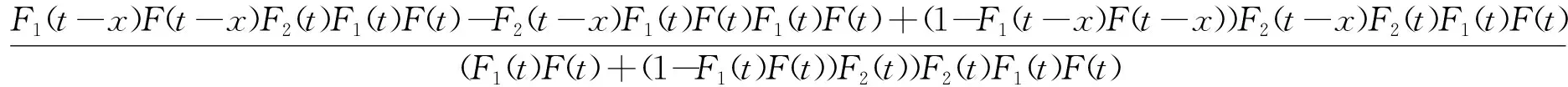
证明完成。
下面的定理显示一定条件下在失效率序下V(t)与V(t)的随机比较。
定理3 设随机变量X1,X2和X相互独立且有相同分布F(x),则V(t)≥hrV(t)。
证明V(t)和V(t)的生存函数分别为


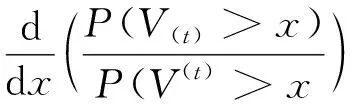
证明完成。
定理4 设随机变量X1,X2和X相互独立,且F1(t-x)F1(t-x)=F2(t-x)=F(t-x)F(t-x),则V(t)≥hrV(t)。
证明V(t)和V(t)的生存函数分别为


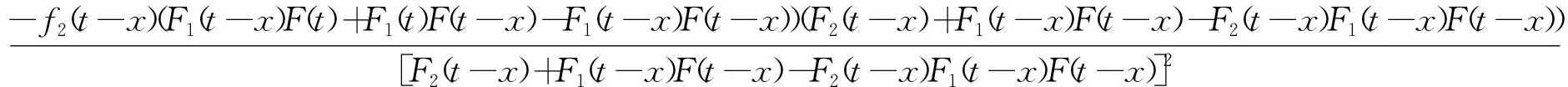

证明完成。
下面的定理显示一定条件下在普通随机序下V(t)与V(t)的随机比较。

证明要证明V(t)≥stV(t),只需证明P(V(t)>x)≥P(V(t)>x),
P(V(t)>x)-P(V(t)>x)
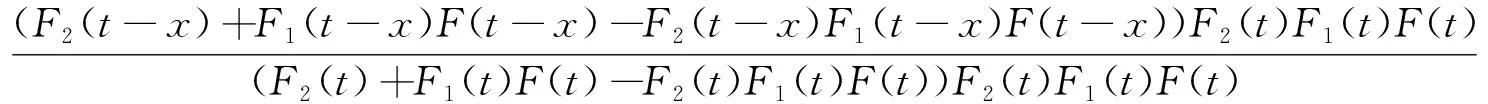


P(V(t)>x)-P(V(t)>x)

证明完成。
2 两个元件分配到两个元件组成的串联系统组成串并联系统的休止时间
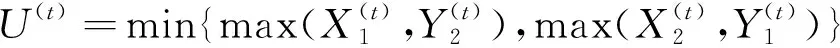
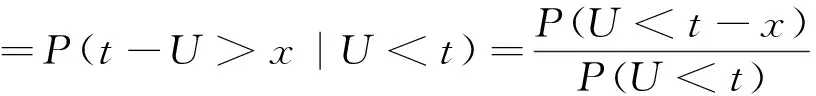
下面的定理显示一定条件下在普通随机序下U(t)与U(t)的随机比较。
定理6 设随机变量X1,X2和Y1,Y2相互独立有相同分布F(x),则U(t)≤stU(t)。
证明要证明U(t)≤stU(t),只需证明P(U(t)>x)≥P(U(t)>x)

证明完成。
3 并联系统的休止时间
设X和Y为相互独立随机变量,其分布函数分别为F(x)和G(x),设并联系统休止时间max(X,Y)(t),max(X(t),Y(t))分布函数分别为
F(x)=P(max(X,Y)(t)≤x)=1-P(t-max(X,Y)>x|max(X,Y) 接下来在反失效率序并联系统的休止时间进行比较。 定理7 设随机变量X,Y相互独立,则max(X,Y)(t)≤rhmax(X(t),Y(t))。 证明完成。 接下来在似然比序并联系统的休止时间进行比较。 定理8 设随机变量X,Y相互独立(不必同分布),则max(X,Y)(t)≤lrmax(X(t),Y(t))。 本文仅研究两个元件组成的串联系统独立情况下,将一个元件和两个元件分配到串联系统中组成串并联系统,得到了休止时间的随机比较结果;对于其它两个元件冗余分配的剩余寿命和休止时间问题可作进一步的研究工作。 致谢:感谢在本文写作过程中西北师范大学数学与统计学院颜荣芳教授给予的帮助!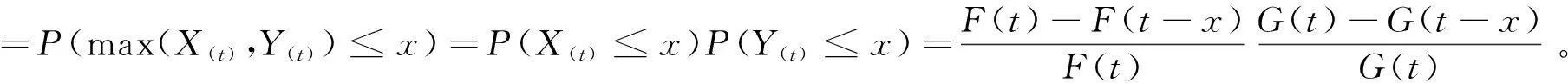




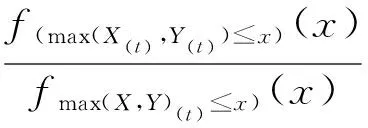


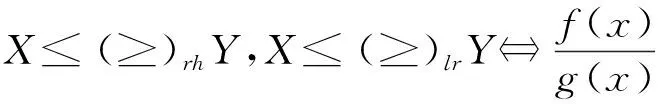
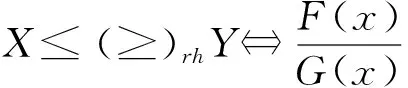
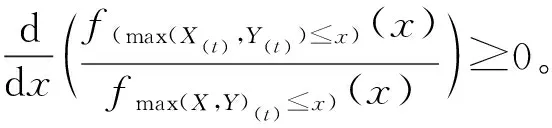
4 结 语
