基于改进教与学算法的含电能路由器的电力系统无功优化
2022-06-06从帆平周建萍茅大钧齐国庆黄祖繁
从帆平,周建萍,茅大钧,齐国庆,黄祖繁
(上海电力大学自动化工程学院,上海市 200090)
0 引 言
随着构建能源互联网战略的提出,风电、光伏等大量分布式能源的广泛接入,改变了电力系统潮流的分布,增加了电网安全稳定运行和优化控制的难度。因此提高电网优化控制能力是现代电力系统需要解决的重要问题之一。柔性交流输电系统(flexible alternative current transmission system,FACTS)是综合电力电子技术、微处理和微电子技术、通信技术和控制技术而形成的用于灵活快速控制交流输电的新技术。FACTS设备可以有效地控制电网的电压和功率,提升电网运行的灵活性。在众多FACTS设备当中,电能路由器(electric energy router,EER)由于具有控制潮流大小和方向、实现带故障隔离的中低压变换、独立设置相关端口电压、连接多层电力系统等功能,成为未来构建能源互联网的关键设备[1-5]。目前电能路由器在结构设计、瞬态仿真和控制策略方面的研究已经比较成熟,但将其应用在电力系统运行优化中的研究并不多见[6-8]。而近几年有多名专家学者提出了以固态变压器为能量交换核心的电能路由器稳态数学模型,这为电能路由器在电力系统运行优化方面的研究奠定了基础[9-10]。同时,面对日益提高的新能源渗透率为电力系统运行所带来的的新难题,将电能路由器引入电力系统,发挥其灵活的潮流控制能力,变得十分有必要。但是,电能路由器的接入使电力系统运行所受的约束条件更多,优化控制方面需要考虑电能路由器和传统电网的协调控制,为电力系统的运行优化带来了新的挑战[11]。近年来,大量专家学者对融合电能路由器的电网运行优化展开了研究。其中,计及电能路由器的电力系统无功优化成为研究人员关注的热点。
无功优化问题本质是含多变量、多约束条件的混合非线性规划问题,求解难度非常大,其求解方法大致可以分为两类:一类是传统的数学优化方法,如线性规划法、非线性规划法、内点法等;另一类是智能优化算法,如遗传算法(genetic algorithm, GA)、粒子群算法(particle swarm optimization,PSO)、人工蜂群算法(artificial bee colony,ABC) 、樽海鞘群算法(multi-objective salp swarm algorithm,MSSA)等[12-14]。随着人工智能技术的发展,智能算法处理非凸、非连续、多峰值问题方面的性能不断提高,逐渐引起了人们的重视。教与学算法(teaching-learning based optimization,TLBO)与其他优化算法相比,具有结构简单、参数少、优化效率高等优点,一经提出便得到了广泛的关注,并发展出了许多改进算法。文献[15]将牛顿法引入传统教与学算法中,利用局部搜索算子增强算法的局部搜索能力,丰富了算法的搜索模式和行为,提高了算法的搜索效率。文献[16]提出了一种自反省的教与学算法,在学习阶段引入一种自我反省的学习策略,实现对本地信息更细致的搜索。文献[17]为学生构建了更加完善的学习架构,在学生完成教学阶段之后,进一步对比与教师和最差学生的差异,自主完成多样化的学习操作,提高算法的寻优精度。但是以上算法在其优化过程中,对教师和学生的依赖性较强,在针对复杂多峰值优化问题时,教师和学生的选择效率较低,容易使算法陷入早熟[18-19]。
鉴于此,本文提出一种融合遗传思想的教与学算法(genetic thought teaching-learning based optimization,GTTLBO)。在教阶段,选择适应度值最高的个体为教师,学生根据与教师的差距调整各科成绩;在学阶段,提出利用遗传思想的轮盘赌选择策略,使每一个学生尽可能选择优秀的同学互相学习,避免无效学习,提高学习效率。在教学完成以后,借鉴遗传算法的变异思想,引入自适应柯西变异,增强学生种群的多样性,避免陷入局部最优。对改进的含电能路由器IEEE RTS-79系统进行仿真分析,以验证GTTLBO算法在无功优化中的可行性和有效性。
1 计及电能路由器无功优化模型
1.1 电能路由器模型
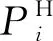
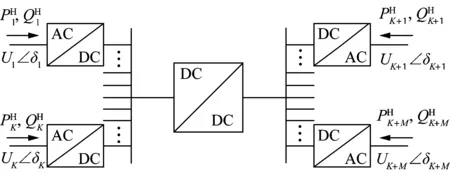
图1 电能路由器的通用拓扑结构
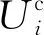

图2 电能路由器端口电力电子结构示意图
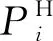
(1)
(2)
(3)
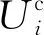
(4)
(5)
式中:ri为综合电压控制系数;μi和Λi分别为直流侧的电压利用率和AC/DC变换器的调制系数。由公式(1)—(5)可知,电能路由器可以通过改变内部参数μi和Λi来影响各个端口注入功率的大小和方向,从而调整与电能路由器端口相连线路的潮流大小与方向,减少潮流的拥塞。
电能路由器中间直流/直流能量交换层的每一侧需要满足有功功率平衡,其具体表达式如下所示:
(6)
电力系统中,电能路由器的控制方式可以选取如下两种基本控制方式之一:
1)维持电能路由器端口的有功和无功功率恒定。
2)维持电能路由器端口的有功功率和所连接的交流电网节点电压幅值恒定。
此外,对于电能路由器而言,需要松弛一个端口的有功功率来满足电能路由器的总体有功功率平衡,该端口被定义为松弛端口。
1.2 目标函数
考虑到电网运行的经济效益和电能质量,建立了以有功总网损F1和电压偏离度F2最小的目标函数,具体如下[22]:
(7)
(8)

(9)
1.3 约束条件
融合电能路由器的电网无功优化问题需要考虑的约束条件如下:
1)交流电网潮流方程。
(10)
(11)
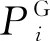
2)直流/直流母线的电压关系。
电能路由器的一次侧和二次侧直流电压满足下列关系:
(12)
(13)

3)电能路由器中间交换层有功功率平衡方程。
(14)
(15)
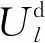
4)变量上下限约束。
无功补偿点的无功补偿容量和节点电压上下限约束:
(16)
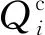
电能路由器端口注入功率上下限约束:
(17)
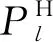
2 基于改进教与学算法的无功优化实现
2.1 基本教与学算法
TLBO分为2个部分,一部分是“教”阶段,即班级的每个学生都向最优个体教师进行学习,根据与老师的差距对各科成绩进行调整;第二部分是“学”阶段,即班级的学生之间进行相互学习,在提升学生成绩的同时可以增强班级种群的多样性。该算法分为以下几个步骤:
1)设置算法参数,初始化班级种群。
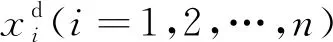
(18)
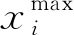
2)“教”阶段。
在班级中选择一位最优秀的个体为教师,其余个体为学生,并根据学生每个科目的平均成绩与教师的差异进行学习。教学阶段的更新公式如下所示:
(19)

完成教学后,对适应度值有所提高的学生进行更新,具体公式如下:
(20)

3)“学”阶段。
每一个学生在班级当中随机选取一位同学进行相互学习,通过相互比较分析进行更新,具体公式如下:
(21)
式中:i≠j,且采用随机的学习步长rand(0,1);xi和xj表示随机选取的2名学生。相互学习完成后,采用教学阶段的更新公式对学生进行更新。
4)如果满足结束条件,则输出结果;否则返回教学阶段继续优化。
2.2 融合遗传思想的教与学算法
2.2.1 “学”阶段改进
在原始教与学算法中,学习阶段随机选取2名学生进行互相学习,若选择的2名学生成绩均较差,则学习效率较低,影响算法的收敛速度。于是本文借鉴遗传思想,利用轮盘赌选择,根据学生的适应度值确定被选中的概率P(xi),使每一位学生尽可能选择较优秀的同学进行相互学习,提升算法的收敛速度。学生选择过程如图3所示,在种群中利用轮盘赌和顺序选择法挑选学生A和学生B进行互相学习,提高学生种群的成绩水平。

图3 轮盘赌选择示意图
轮盘赌选择策略操作流程如下:
1)根据式(22)计算每个个体被选中的概率。
(22)
2)根据式(23)计算每个个体的累计概率q(xi)。
(23)
3)在[0,1]区间产生一个随机数rand,如果0≤rand≤q(xi)或xi≤rand≤q(xi+1),则选择第i个个体。
2.2.2 自适应柯西变异
在该算法的教学阶段,学生只向最优个体与周围同学学习,若算法解集中的学生种群多样性较差,则种群容易向局部最优位置聚集,使算法陷入局部最优解。因此,借鉴遗传思想的变异操作,在教与学算法中引入柯西变异算子。相比于高斯变异,柯西密度函数位于中心点处的峰值更小,但两边趋于零的速度要比高斯变异慢,由此可见柯西变异具有更强的扰动能力,变异后的种群具有更强的多样性,从而较容易使算法跳出局部最优。
一维的柯西变异概率分布函数为:
(24)
式中:t为当前迭代次数。
已知的柯西变异的公式为:
xi=xi+β×C(0,1)
(25)
式中:β为算法的变异步长;C(0,1)为标准柯西分布函数。
在算法前期,较大的变异步长有利于算法的全局寻优。在算法后期,较小的变异步长有利于提高算法的寻优精度。因此,变异步长β应该随着算法迭代次数的增加而逐渐减小。改进的变异公式如下:
(26)
式中:titerationmax表示最大迭代次数。
综上所述,图4展示了改进教与学算法中学生种群的进化过程,其中学生j(j=1,2,3…,N)为初始班级中的学生,学生j′(j′=1,2,3…,N)为经历“学”阶段后的学生群体,学生j″(j″=1,2,3…,N)为经柯西变异之后的学生群体。
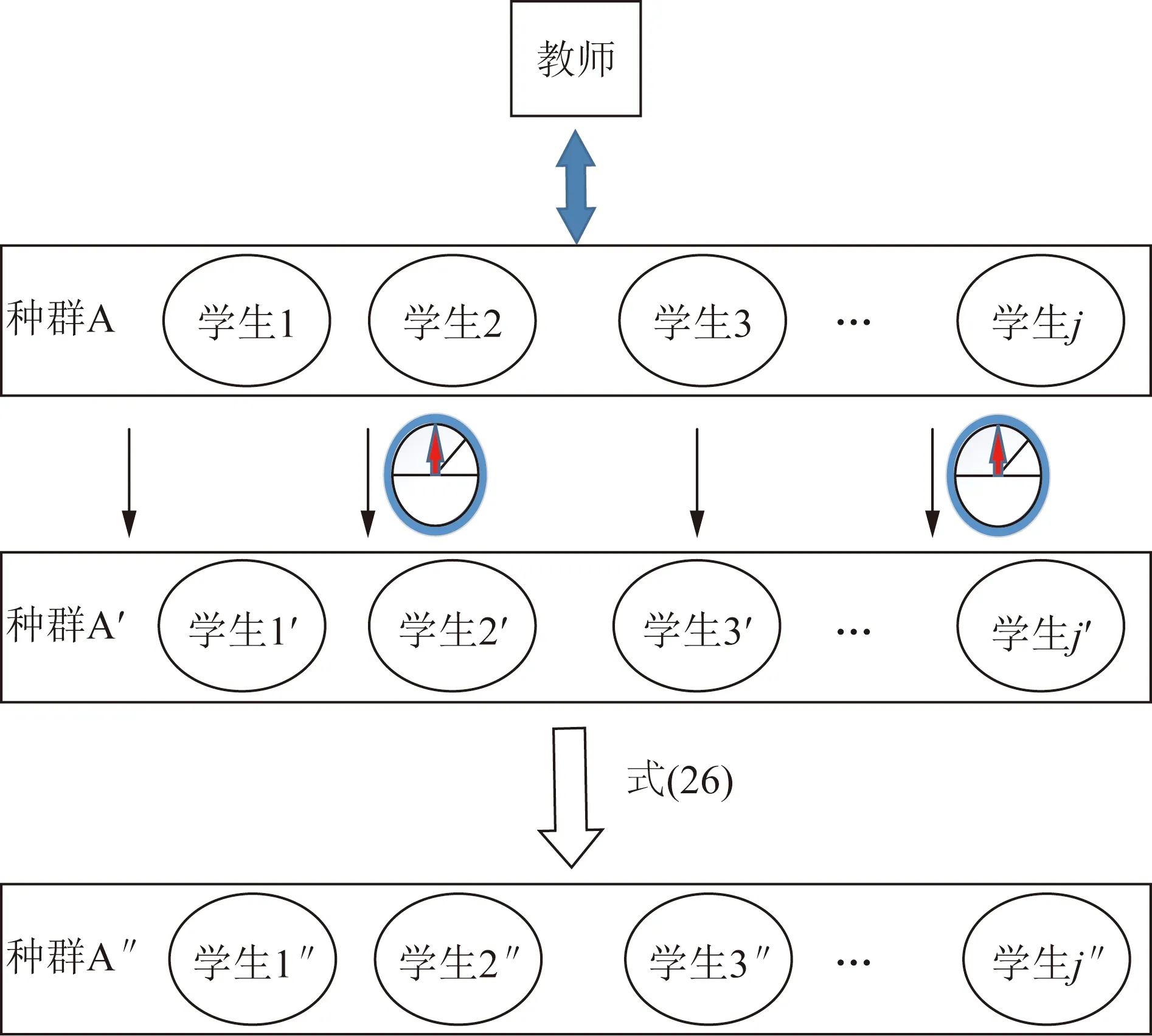
图4 种群进化过程
3 算例分析
3.1 IEEE RTS-79测试系统参数配置
本文采用修改后的IEEE RTS-79测试系统来验证所提出的电网无功优化算法。该测试系统的结构如图5所示,图6给出了系统中发电机出力情况,电网线路相关参数见文献[23]。
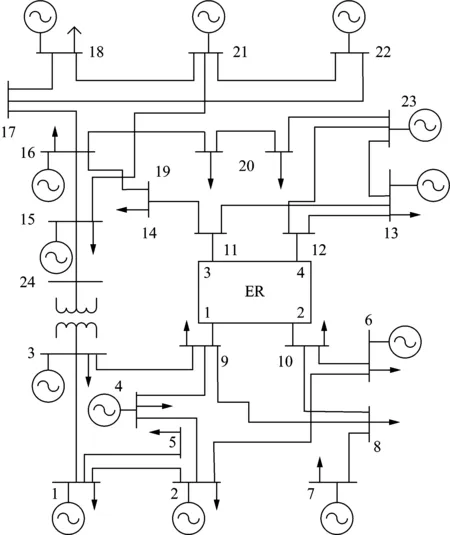
图5 修改后的IEEE RTS-79测试系统
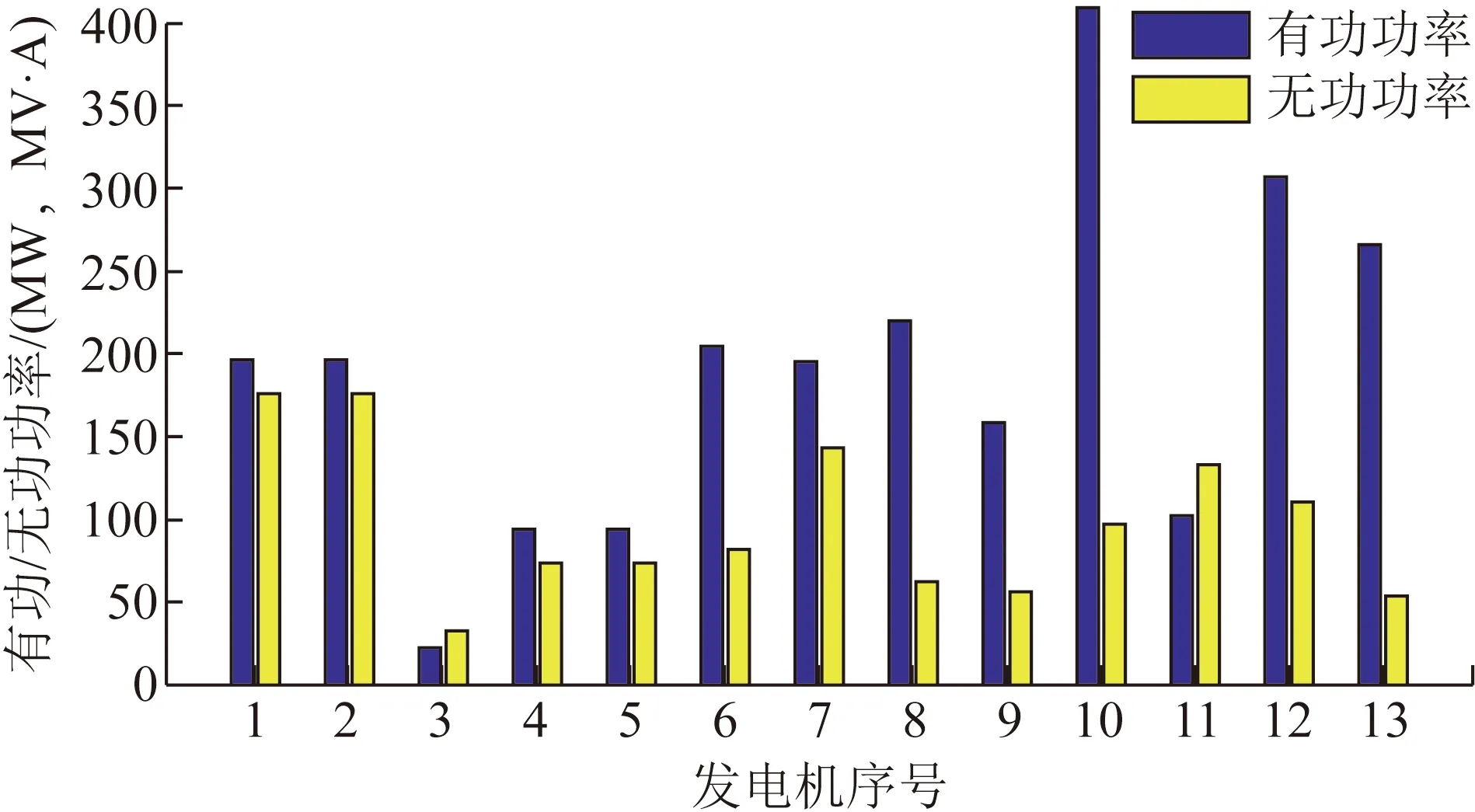
图6 发电机出力数据
本算例中电能路由器额定容量为350 MV·A,系统基准容量为100 MV·A,每个端口均采用恒定有功/无功功率控制模式,一次侧和二次侧的额定电压分别为138 kV和230 kV。节点7、节点15、节点22为无功补偿点,分别安装10组容量为5 MV·A的无功补偿器,补偿器的变化范围为0~0.5 pu。根据电能质量的要求,本文采用的节点电压范围为0.95~1.10 pu。
3.2 电能路由器功能分析
相对于传统电力系统需要通过调节发电机出力来改变线路潮流,含电能路由器的电力系统在潮流的优化控制方面具有一定的优势。算例测试了3种不同控制场景下的电网潮流计算结果,在这3种控制场景下,电能路由器的端口参数设置如图7所示。对于这3种场景,选择以下稳态参量作为观测对象:1)节点6到节点10之间线路的有功潮流;2)节点9的电压幅值; 3)系统的总有功损耗; 4)系统的总电压偏离度。
图8对比了融合电能路由器电网和原始电网相关端口和线路的潮流情况。通过分析基准场景和场景1可知,和电能路由器不参与运行的系统相比,通过引入电能路由器并将相关参数控制为图7中场景1具体控制值,可以使得节点6到节点10之间线路的有功潮流从56.42 MW降低到35.12 MW,并且节点9的电压幅值能从0.947 1 pu提升到1.007 5 pu。
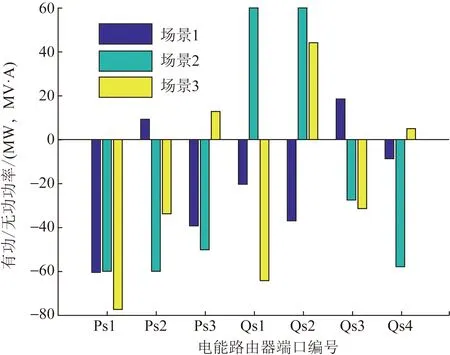
图7 电能路由器端口参数设置
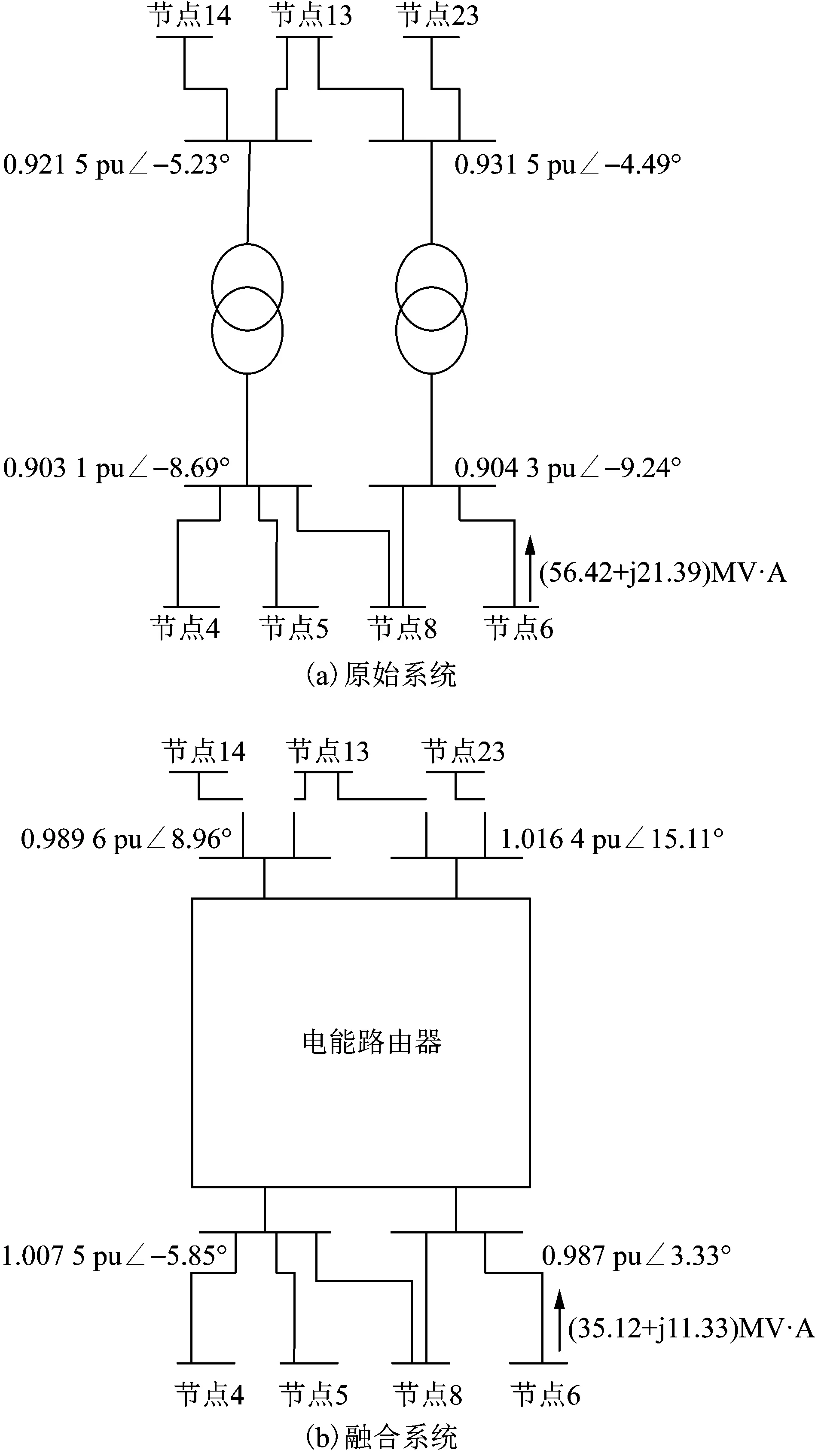
图8 原始系统和计及电能路由器系统的运行状态对比
表1对比了融合电能路由器电网和原始电网相关端口和线路的有功网损和电压偏离度情况。通过分析基准场景和场景1—3的计算结果可知,通过引入电能路由器并将相关参数控制为场景1—3具体控制值,系统有功网损和电压偏离度均实现了大幅下降。不同场景下的潮流计算结果表明,通过调节电能路由器的端口功率参数,可以改善系统运行状态,实现降低电网阻塞,提升节点电压质量,降低系统网损。
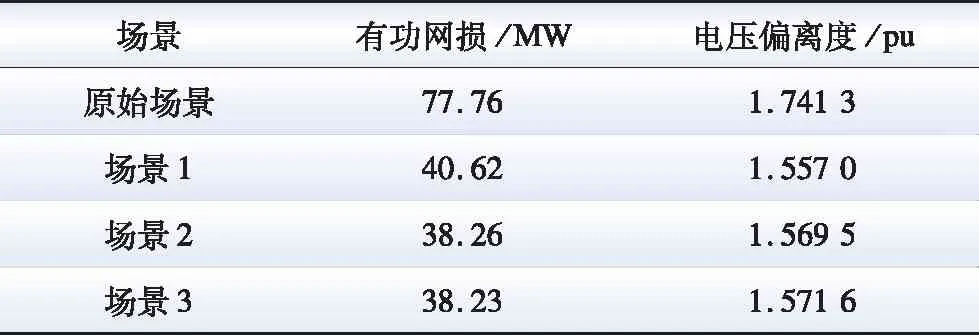
表1 不同场景下电能路由器端口参数的计算结果
为分析电能路由器在无功优化中的经济效益,对比了安装电能路由器前后电容器组的无功补偿容量,对比结果如图9所示。结果表明,安装电能路由器后,电力系统的总无功补偿容量降低了56.25%,极大地降低了电力系统的运行成本。
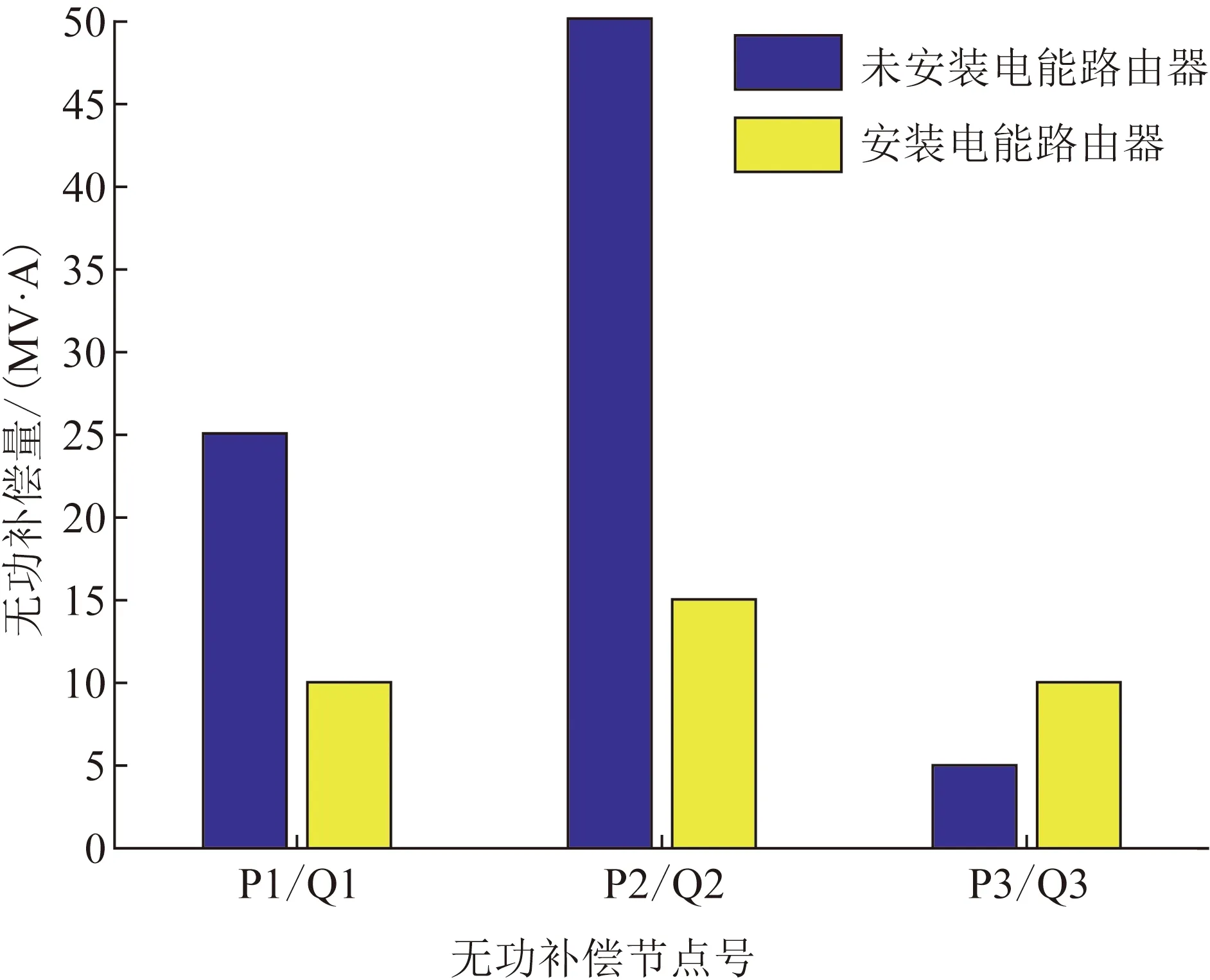
图9 电容器组的无功补偿容量
3.3 算法性能分析
为验证GTTLBO算法求解计及电能路由器电网无功优化模型的有效性,本文采用多种算法进行无功优化并对优化结果进行比较分析。不同的算法各自独立运行,得出的无功优化统计结果如表2所示。每种算法关于有功网损和电压偏离度的进化曲线如图10、11所示。
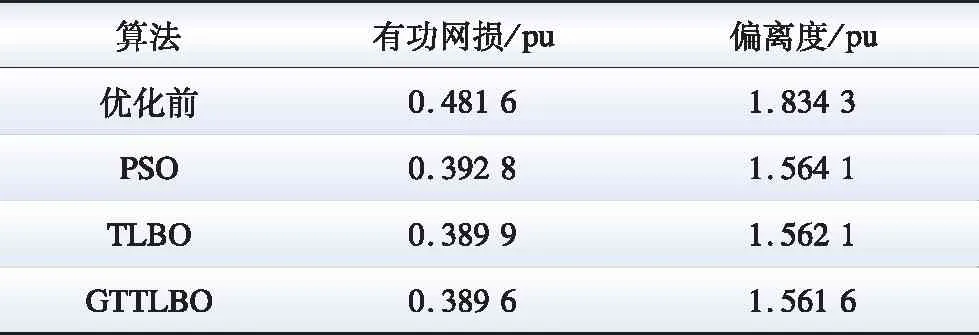
表2 无功优化的统计结果
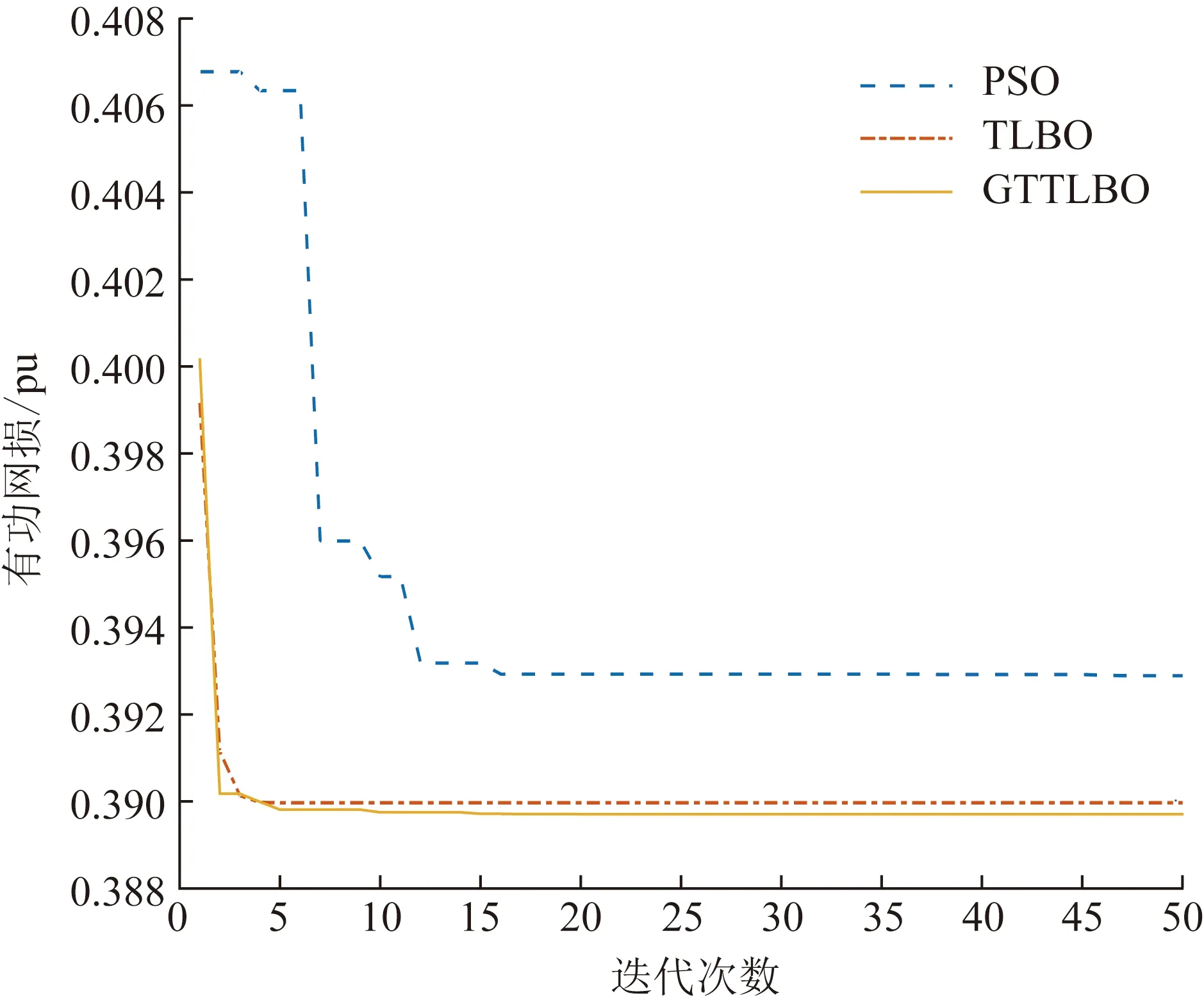
图10 IEEE RTS-79节点系统有功网损
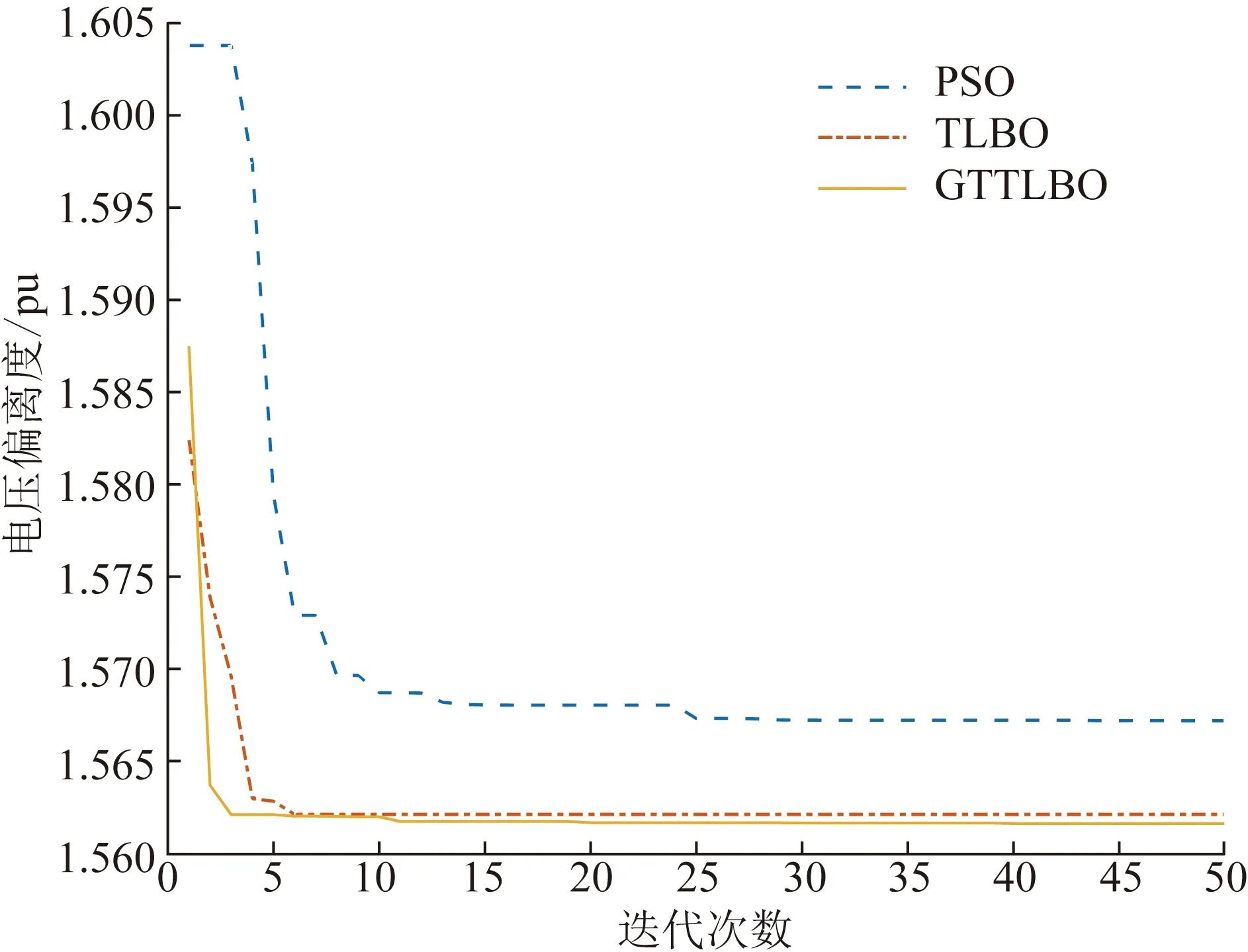
图11 IEEE RTS-79节点系统电压偏离度
从优化结果可以看出:
1)采用GTTLBO算法进行无功优化后的网损为38.96 MV·A,与优化前相比,网损下降了23.61%,电压偏离度为1.561 6 pu,与优化前相比下降了14.86%,优化效果均优于PSO算法和TLBO算法。
2)TLBO算法在进化过程中,虽然收敛速度较快,但是在进化到第3代时便陷入了局部最优,而GTTLBO算法在进化的过程中始终保持良好的种群多样性,在第7代和第11代搜索出最优解。
优化前后电力系统各节点电压对比如图12所示,发现仿真模型中设置的罚函数可以对出现越限情况的状态变量进行处罚。由数据结果可得,优化前节点14、19、20均低于安全电压下限,经过优化后,所有节点电压均维持在安全范围内。

图12 IEEE RTS-79节点系统各节点电压
4 结 论
本文建立了计及电能路由器的电力系统协调无功优化模型,基于IEEE RTS-79节点系统,以有功网损和电压偏离度最小为目标函数,采用改进教与学算法进行仿真分析,得到如下结论:
1)建立计及电能路由器的电力系统协调无功优化模型,得到系统最佳运行策略,能够有效减小系统的有功网损和电压偏离度,提高电网的运行效益和电能质量。
2)引入轮盘赌选择和自适应柯西变异策略,能够保持原始教与学算法收敛速度快的优点,同时解决容易陷入局部最优解的问题。
本文考虑的是某一时刻的无功优化问题,在后续的研究当中应考虑一段时间内的分布式能源出力不稳定性以及储能的功率约束。
