考虑碳税与碳交易替代效应的电力系统低碳经济调度方法

2022-06-06张菁林毓军齐晓光苗世洪张倩茅董家盛陈宇

电力建设 2022年6期

张菁，林毓军，齐晓光，苗世洪，张倩茅，董家盛，陈宇

(1. 国网河北省电力有限公司经济技术研究院，石家庄市 050024；2. 强电磁工程与新技术国家重点实验室(华中科技大学电气与电子工程学院)，武汉市 430074；3.电力安全与高效湖北省重点实验室(华中科技大学电气与电子工程学院)，武汉市 430074)

0 引言

随着人类社会工业化进程的不断推进，全球变暖问题日益严峻，给人类生存与发展带来的负面影响逐渐凸显。中国作为世界能源主要消耗国家，面向气候变化问题开展了大量节能减排工作。2021年，“碳达峰、碳中和”被写入政府工作报告，我国承诺“争取在2060年前实现碳中和”[1-2]。然而，我国产业结构仍以资源密集型和劳动密集型为主，经济社会的发展对高碳能源的依赖性仍然较强。国际能源署的调查报告指出，我国的二氧化碳排放主要来源于以煤炭为主的能源行业，其中，电力行业碳排放量约占全国碳排放量的一半[3-4]。因此，亟需对电力系统现有能源结构进行调整与优化，深入研究电力系统碳减排策略。

对于电力系统而言，碳排放具有负外部性，其本身对系统运行经济效益并没有直接影响[5]。因此，需要由政府主导制定碳规制来约束电力系统碳排放行为，从而提高系统减排积极性。目前大体上存在两类碳规制：碳税制和碳交易制。其中，碳交易制主要是通过市场碳交易价格调控来达到碳减排的目标；而碳税制则是对碳排放量强制收取税收，通过高昂的碳排放成本促使排放主体改变消费能源结构[6]。

针对碳规制影响下电力系统如何优化运行的问题，国内外学者已经开展了大量的研究。文献[7-8]通过建立考虑碳交易市场的虚拟电厂报价模型和风电储能协同优化模型，表明碳交易机制能够有效调整消费能源结构，提高清洁能源利用占比。文献[9]构建了发电-售电的电力供应链模型，识别了阶梯型碳税制对可再生能源投资决策的影响。文献[10-11]分析了碳税制对发电机组出力均衡以及碳排放水平的影响，证明了合理的运行方法可以提高碳税制下系统的碳减排积极性。

上述研究对碳规制背景下电力系统低碳经济调度模型的建立具有指导意义。然而，现有文献大多聚焦于单一碳规制下系统优化运行方法，较少研究涉及到碳税和碳交易替代效应的建模过程，且往往忽略了碳交易价格波动对电力系统低碳调度策略的影响。已有资料表明，以碳税与碳交易为主的复合碳规制已经在诸多国家和地区得到了积极应用。在2008年，挪威政府对能源行业、航空行业等大工业用户的碳排放政策进行了调整，在保持征收碳税的基础上将其覆盖进欧盟碳排放交易体系，通过结合2种机制更好地实现了碳减排的目标[12]。随后，丹麦、芬兰等国家在征收碳税的同时也将高排放工业纳入了欧盟碳排放交易体系[13]。结合实践经验，文献[14-15]研究表明碳交易与碳税复合策略较单一碳规制效果更优，协同应用碳税与碳交易两种碳规制，能够在保证减排目标实现的同时缓和碳减排压力与排放主体经济效益之间的矛盾。同时，文献[16]指出，碳价大幅度波动会给碳减排策略收益带来不确定性，影响碳减排主体的经济效益。因此，如何定量分析碳税和碳交易二者之间的替代效应，建立考虑碳价不确定性的系统优化运行模型，为制定低碳经济调度策略提供指导，仍有待进一步研究。

为此，本文首先采用随机场景法描述碳价不确定性，在此基础上，对阶梯型碳税与碳交易替代效应进行建模；其次，建立考虑灵活碳捕集设备与储能电站协调互动的两阶段低碳经济调度模型，并采用蝙蝠优化算法求得不同碳价场景下的最优解。最后，通过算例仿真，验证考虑阶梯型碳税与波动价格碳交易替代效应的优化模型可以有效提高电力系统运行的经济-环境联合效益。

1 阶梯型碳税与波动价格碳交易替代效应模型

1.1 系统碳排放成本模型

在碳交易与碳税复合碳规制环境下，电力系统根据火电机组的发电量获取无偿分配的初始碳排放配额[17]。本文采用基准线法确定系统的初始碳排放配额QGP，如式(1)所示：

(1)

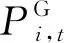
本文假定系统从电力市场购买的电量均来源于火电机组，因此，所考虑的电力系统碳排放量主要有2个来源，分别由外购的电力以及火电机组燃煤产生。为了便于求解，本文忽略了火电机组碳排放系数中的二次项，如式(2)所示：

(2)

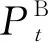
当一个调度周期内电力系统产生的碳排放量超过初始碳排放配额后。系统需要选择在碳交易市场中购买碳排放许可证或者为部分碳排放量支付碳税，从而产生额外的碳排放成本，如式(3)—(5)所示:

QT=QGP+QTA+QTR

(3)

QTR=μ(QT-QGP)

(4)

CT=CTA+CTR

(5)

式中：QTA为系统分配于支付碳税的碳排放量；QTR为分配于购买碳排放许可证的碳排放量；μ为替代系数；CT为总碳排放成本；CTA、CTR分别为碳税成本和碳交易成本。

1.2 碳交易成本函数

在碳交易市场中，受到市场供给、排放需求等众多因素的影响，碳排放许可证购买价格呈现出不确定性[18]。文献[19]通过实证分析表明碳价不确定性拟合度最优的是几何布朗运动，如式(6)所示：

dPctra(t)=ρPctra(t)dt+σPctra(t)dB(t)

(6)

式中:dPctra(t)为碳价的不确定性量；ρ为碳价的期望增长率；Pctra(t)为t时刻碳价；dt为时间增量；σ表示碳排放权交易价格波动率；B(t)为标准维纳过程，dB(t)为标准维纳过程增量。

考虑到碳价不确定性存在大量公开且具有可信来源的历史数据，且碳价波动主要影响系统运行的经济效益。因此，本文基于随机场景法对碳价不确定性进行建模。

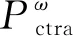
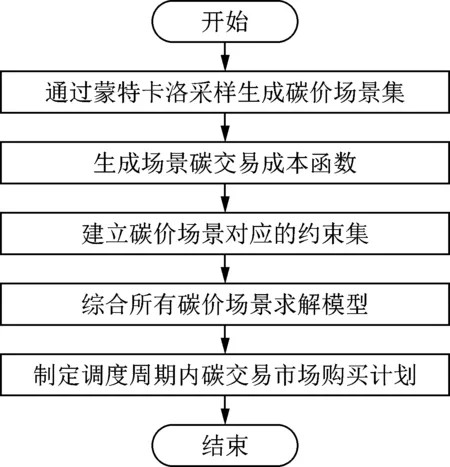
图1 基于随机场景法的碳价不确定性建模

(7)

基于碳交易成本函数，电力系统作为碳交易市场中的价格接受者，为每个碳价场景建立对应的约束集合。综合所有碳价场景下的约束集合和碳交易成本函数，系统统一求解低碳调度模型，获取调度周期内每个碳价场景对应的调度计划、替代系数以及分配于购买碳排放许可证的碳排放量，从而制定考虑碳价不确定性的碳交易市场购买计划。

1.3 阶梯型碳税成本函数

在现行的碳税制中，税率主要有两种计量标准：一种是以排放主体的排放量独立计量；另一种是按碳交易价格的比例进行计算[21]。本文采用第一种碳税标准，即碳税税率取决于系统分配于支付碳税的碳排放量，从而消除碳税成本与碳交易成本之间的耦合关系，便于分析碳税与碳交易两种碳规制之间的替代效应对电力系统运行效益的影响。

为了提高电力系统碳减排积极性，本文在构建碳税成本计算模型中引进阶梯型碳税，通过对系统超过初始配额的碳排放量收取阶梯式增高的碳税，从而充分挖掘系统低碳减排潜力。

阶梯型碳税税率示意图如图2所示。阶梯型碳税将系统分配于支付碳税的碳排放量分成多个区间。随着碳排放量的增加，阶梯型碳税的税率逐渐增大(图2中体现为各区间纵轴的函数值RTA)。

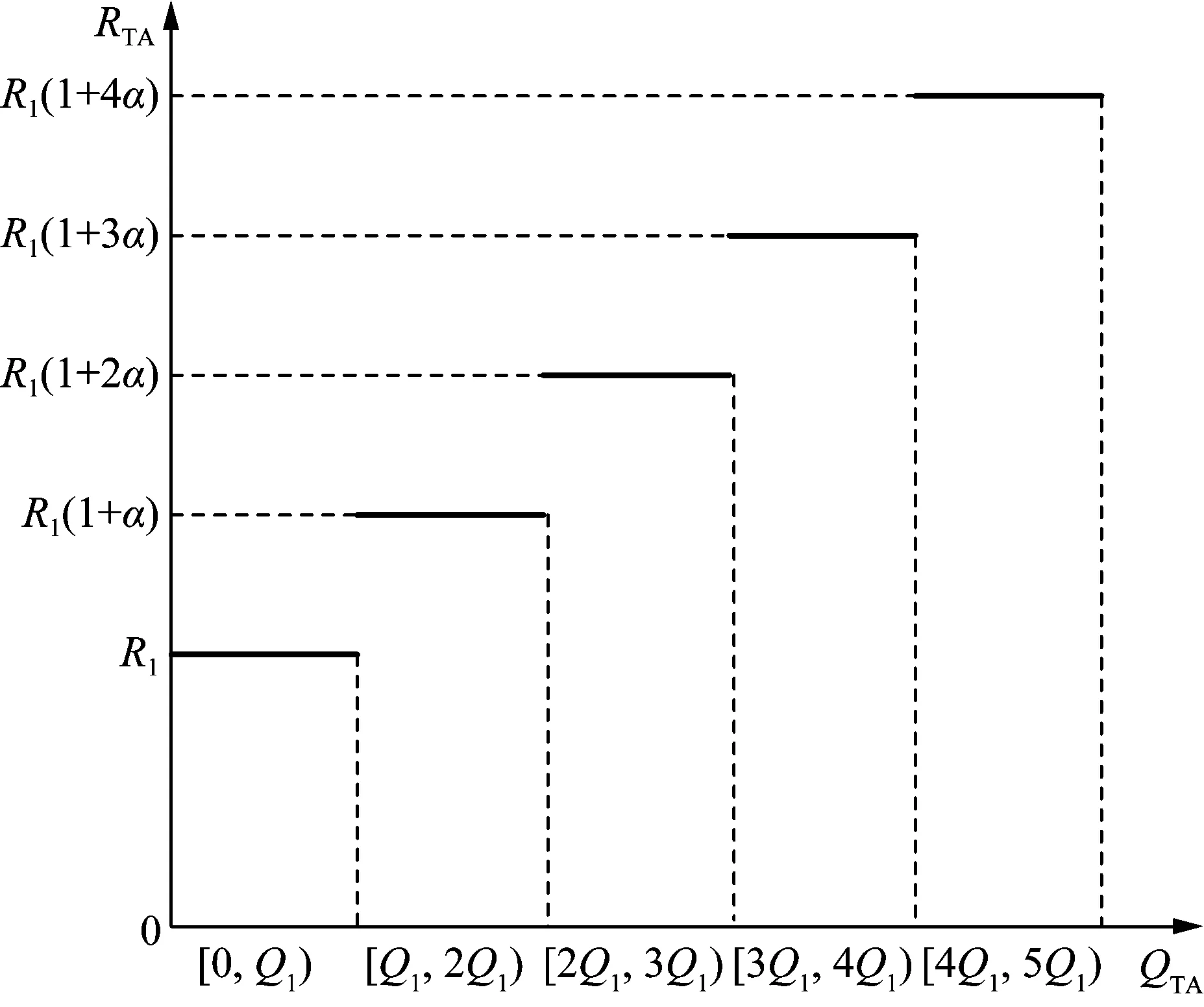
图2 阶梯型碳税

根据递进式的阶梯型碳税税率，可以获取碳税成本函数，如式(8)所示。

(8)

式中：R1为基础税率；Q1为碳税区间长度；α为税率增长幅度。

图2只列出了碳排放量大于零时的情景，对于初始碳排放配额充足的情景，系统只允许在满足自身碳排放量需求后在碳交易市场出售多余的碳排放权。

在构建波动价格碳交易成本函数和阶梯型碳税成本函数的基础上，只需对电力系统进行低碳经济优化，获取系统调度周期内碳排放量、碳排放配额以及替代系数后，即可求解系统支付的碳排放成本。

2 模型构建

2.1 模型目标函数

本文所考虑的电力系统主要由风电光伏机组、火电机组、储能电站以及碳捕集设备构成。系统以风光机组和火电机组为主要发电来源，同时，向互联电力市场购买电量来满足系统负荷需求。储能电站安装在风光出力侧，通过能量时移特性为风光机组出力波动提供电能补偿。碳捕集设备安装在火电机组侧，与火电机组一同构成碳捕集电厂，减少机组发电过程碳排放量。

其中，碳捕集设备采用灵活运行模式，并同时配备储液罐实现碳捕获能耗时移。

电力系统低碳经济调度模型的优化目标是在计及碳排放成本的基础上，使调度周期内系统总运行成本最小。考虑到系统中火电机组的启停状态在日前确定之后无法根据场景碳价的改变而做出调整。因此，模型将优化目标函数分为第一阶段的火电机组启停成本和第二阶段的火电机组运行成本、购电成本以及碳排放成本之和。

系统低碳经济调度模型的目标函数为：

(9)

2.2 模型约束条件

面向所研究的低碳经济调度模型，本节主要考虑包括碳捕集设备运行约束、储能电站运行约束、火电机组运行约束、系统及网络功率平衡约束等约束条件。

1)碳捕集设备运行约束。

火电机组可以通过安装碳捕集设备组成碳捕集电厂，从而实现煤燃烧后二氧化碳的捕获与存储，避免其排放到大气中。本节采用捕获水平灵活以及配置储液罐的碳捕集设备，通过设备运行能耗时移来降低系统的运行成本。

碳捕集设备的总能耗包括固定能耗和运行能耗，其中，运行能耗与碳捕集设备解析及压缩捕获的二氧化碳量有关，如式(10)所示：

(10)

火电机组输出功率部分被碳捕集设备所消耗，因此，碳捕集电厂总输出功率为：

(11)

在碳捕集设备采用捕获水平灵活并配置储液罐的条件下，设备捕获的二氧化碳量由两部分组成，从火电机组煤燃烧中吸收的碳排放量，以及储液罐释放或储存的碳排放量，如式(12)所示：

(12)

其中，为了维持碳捕集设备在运行时的稳定性，需要设定捕获水平的最小、最大值，如式(13)所示：

(13)

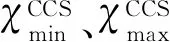
在配置储液罐的条件下，碳捕集设备可以利用乙醇胺等溶剂溶解部分二氧化碳，暂时储存在富液罐中。在其余时段，设备可将富液罐中的溶液运送至气提塔进行释放捕获，从而将部分高电力需求时段的捕获能耗转移到低电力需求时段，提高系统运行灵活性[22]。本文模型采用乙醇胺溶液作为储液罐溶剂，其单位二氧化碳溶解所需溶液体积如式(14)所示：

(14)

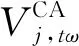
假设溶剂存储和提取过程不同时进行，结合乙醇胺溶液消耗体积可得储液罐中富液罐、贫液罐的体积计算表达式以及溶液体积上下限约束。

(15)

2)储能电站运行约束。

通过建立储存电量、充放电功率和始末储存能量平衡约束，可对储能电站的运行特性进行建模。

储能电站充放电功率约束：

(16)

储能系统容量约束：

(17)

式中：Es,tω为场景ω下t时刻储能电站s的储能状态；ε为储能电站自损耗率；ηC为充电效率；EA为储能电站总容量；Emax、Emin为容量状态的上下限值。

始末储存能量平衡约束：

|Es,Tω-Es,0ω|≤ΔE

(18)

式中：Es,0ω、Es,Tω代表储能电站s初始时刻和末尾时刻的容量状态；ΔE为始末时刻允许的容量偏差值。

3)系统及网络功率平衡约束。

线路潮流约束：

(19)

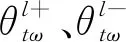
线路潮流上下限约束：

-Fl,max≤fl,tω≤Fl,max

(20)

式中：Fl,max为线路l潮流限值。

系统功率平衡约束：

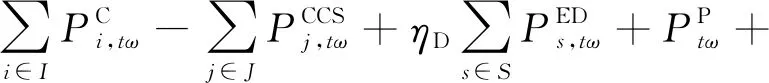
(21)

此外，火电机组约束及购电市场约束可参见文献[23-24]，在此不再赘述。

3 模型优化求解方法

考虑阶梯型碳税和波动价格碳交易替代效应后，调度模型变成一个非线性且存在变量相乘的混合整数非线性优化模型，难以进行有效优化求解。因此，本节首先对阶梯型碳税进行分段函数线性化处理，进而得出碳税成本函数表达式。在此基础上，采用蝙蝠优化算法处理变量相乘问题，通过智能算法搜索获取不同场景下的最优替代系数，从而制定电力系统低碳经济调度计划。

对于递进式阶梯型碳税税率，本节结合辅助连续变量和0-1变量进行分段函数线性化。根据式(8)所示的五分段税率，结合5个0-1变量zi和6个连续变量wi将系统分配于支付碳税的碳排放量以及碳税成本进行线性化表述，如式(22)所示：

QTA=Q1w2+2Q1w3+3Q1w4+4Q1w5+5Q1w6

(22)

进一步，结合阶梯型碳税税率在分段点的函数值可得碳税成本。

CTA=R1Q1w2+R1Q1(2+α)w3+R1Q1(3+3α)w4+R1Q1(4+6α)w5+R1Q1(5+10α)w6

(23)

其中，辅助变量需满足式(24)约束。

(24)

结合式(22)—(24)的转化，可将连续分段的碳税成本进行线性化表述。随后，本文采用蝙蝠优化算法处理变量相乘问题，通过启发式算法搜索不同场景下的最优替代系数，得到系统优化调度计划。

在优化算法中，蝙蝠个体位置代表一组替代系数的可能取值。算法将替代系数传递给多场景电力系统低碳调度模型，模型根据替代系数取值进行优化求解，获取系统运行成本作为蝙蝠个体的适应度[25]。在获取所有蝙蝠个体的适应度后，算法对每个蝙蝠个体的频率、位置和速度进行更新，并记录最优适应度的个体。算法通过不断迭代更新蝙蝠个体参数并计算其适应度，从而得到优化后的替代系数以及对应的系统调度计划。算法具体实施流程如图3所示。

图3 蝙蝠算法优化流程

结合分段函数线性化表述和蝙蝠优化算法处理，将本文优化主体问题转换为混合整数线性规划问题，利用常用的商业优化软件即可进行求解。本文采用Pycharm2019.3.x64调用Gurobi求解器实现模型优化。

4 算例分析

4.1 算例参数设置

本文基于某地区的实际参数进行仿真分析，网架结构如图4所示。其中，将火电厂G1—G4改造为碳捕集电厂，风电光伏接入节点分别为节点36与节点31，并在风光接入节点同步配置储能电站。系统与外界电力市场的联络线接入点为节点30。

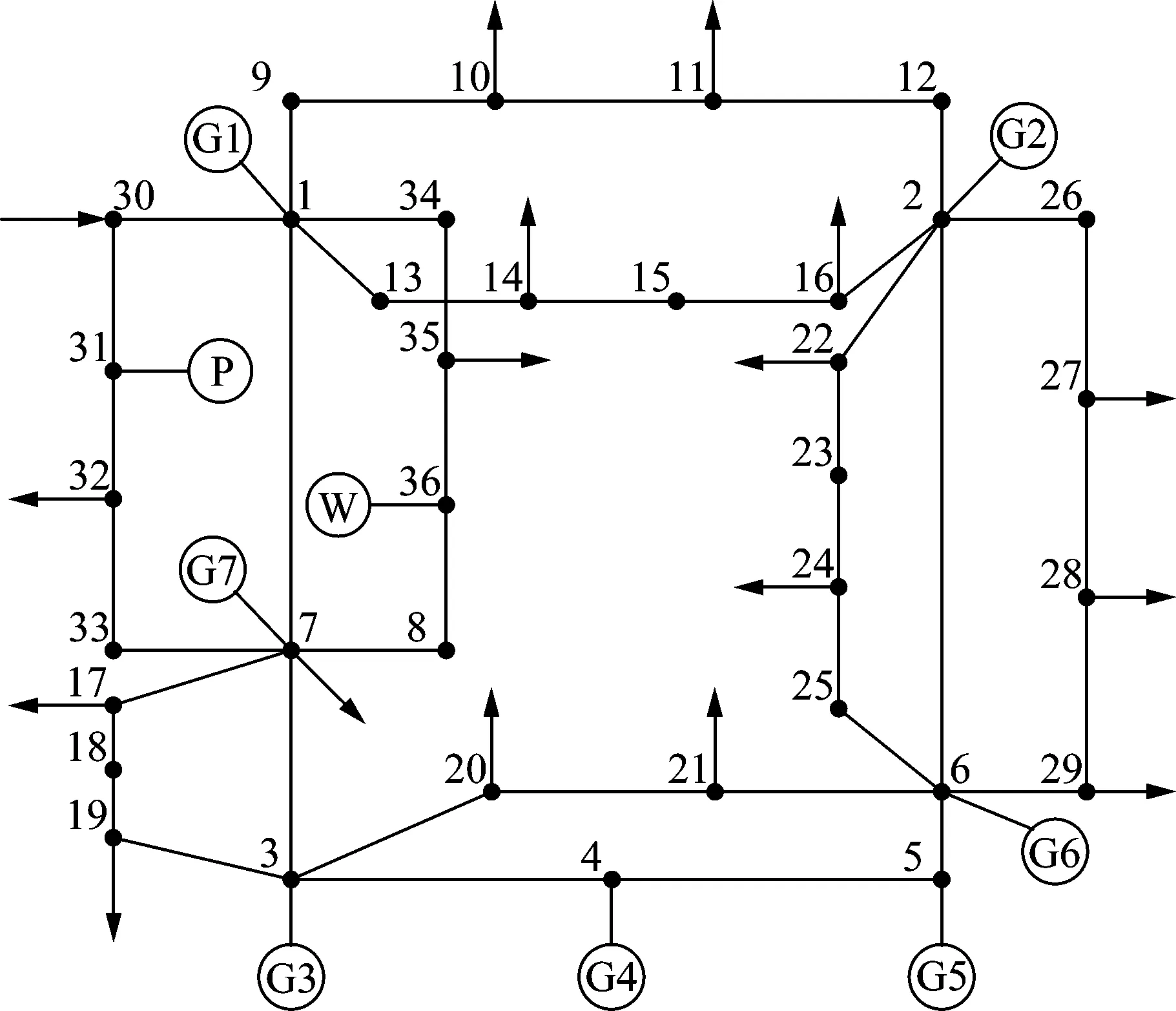
图4 系统网架结构

购电市场采用峰谷平分时电价形式，其中，谷时段00:00—09:00、23:00—24:00，电价为0.37元/(kW·h)，平时段09:00—12:00、21:00—23:00，电价为0.76元/(kW·h)，峰时段12:00—21:00，电价为1.08元/(kW·h)[26]。外购电量的碳排放计算参数取0.78 t/(MW·h)。碳交易市场中期望碳排放权交易价格为45元/t。由于本文所建模型为电力系统日前调度模型，因此，几何布朗运动方程中的时间增量dt=1天，μ=1，σ=0.47[18]。火电机组、碳捕集设备、储能电站以及其他设备参数详见文献[27-28]。

4.2 模型优化结果分析

根据碳交易价格不确定性的拟合方程式，模型采用蒙特卡洛模拟法进行场景抽样，抽取出的碳交易价格场景如图5所示。

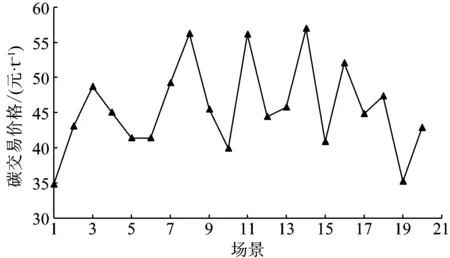
图5 碳交易价格场景

以碳交易价格场景1为例，模型调度周期内的火电机组出力、碳捕集设备能耗、储能电站充放电功率以及购电功率如图6所示。

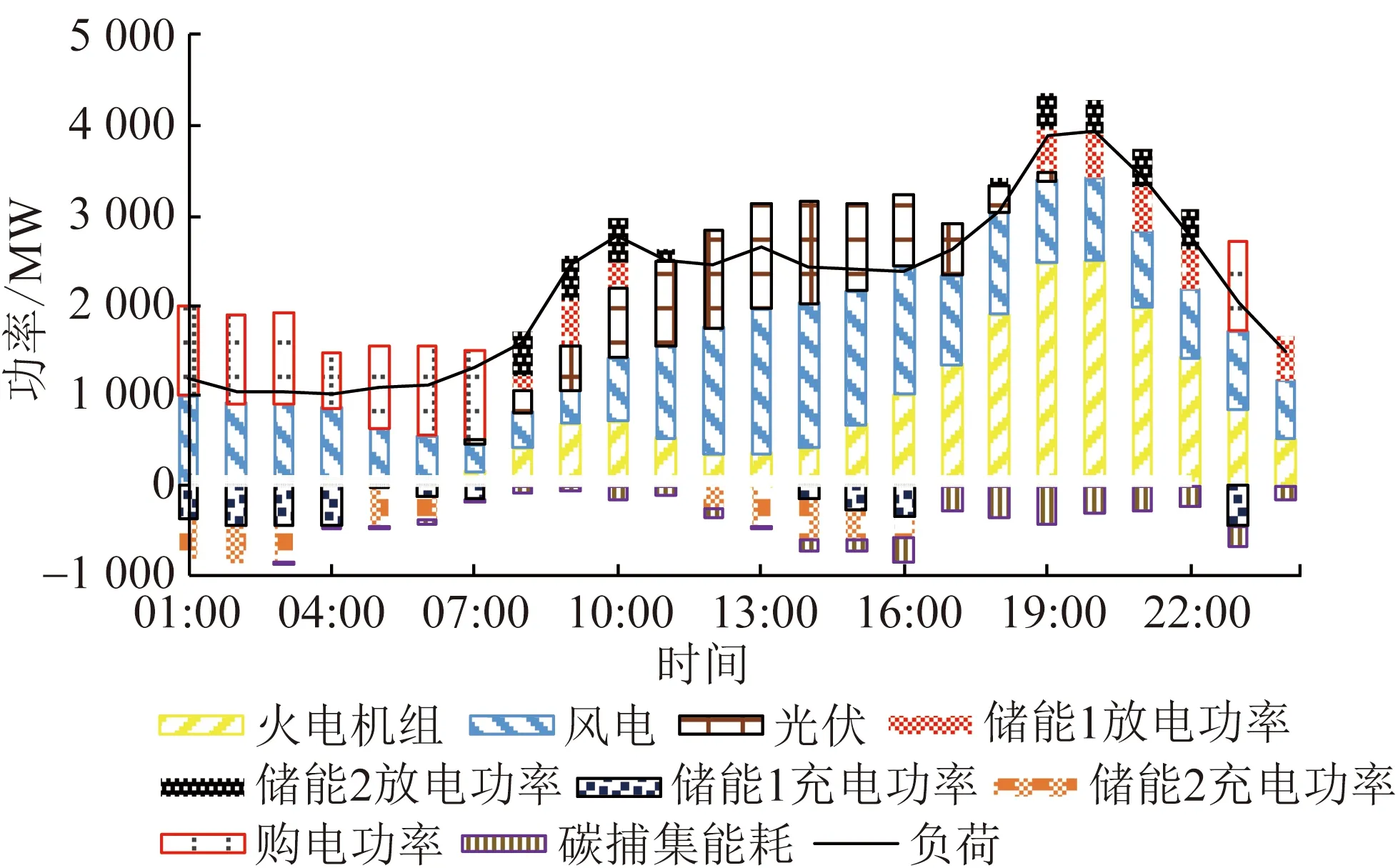
图6 场景1下系统调度结果

从场景1的调度结果可以看出，在01:00—08:00时段以及23:00—24:00时段，由于系统负荷较小，且购电市场大多处于谷时段电价区间，因此负荷需求主要由风光机组出力和购电功率满足。而在10:00—22:00时段，系统负荷需求功率上升，购电价格升高，购电平均成本大于火电机组发电成本，系统通过增加火电机组出力来满足地区负荷供电需求。储能电站在负荷低谷期和电价较低的时段储存多余电能，而在用电高峰期释放电能满足部分负荷需求。此外，碳捕集设备通过消耗部分火电功率，捕集机组排放的二氧化碳并进行封存处理，从而有效降低碳捕集电厂自身碳排放量。结果表明模型通过整合低碳调度资源，协调不同设备出力，可有效挖掘系统运行的经济性和低碳性。

图7为不同碳交易价格场景下系统的碳排放量构成。由于本文假定系统外购电量均来源于火电机组，并计算其碳排放参数，因此，碳规制整体强度的增加会使得系统在电价谷时段减少从电力市场购买的电量，增加系统内部火电机组的出力，降低系统的碳排放惩罚成本。对比碳价较高的场景8、14和16和碳价较低的场景1和19可以看出，随着碳交易价格的提高，一方面，系统会倾向于使用火电机组发电替代从电力市场中购买电量，另一方面，碳捕集设备的碳捕获量也随之增加，降低了火电机组向系统中注入的发电功率，系统通过增加发电成本来减少调度周期内的剩余碳排放量。结合不同场景的调度结果可以看出，由于碳交易市场成交的碳排放权价格存在不确定性，因此，电力系统应该充分考虑碳交易价格的波动性，根据不同的碳排放权价格灵活制定调度计划，从而有效协同整合系统内部调度资源，实现优势互补，提升系统运行的经济-环境效益。

图8和图9分别为不同碳交易价格场景下系统剩余碳排放量分配结果以及替代系数、系统剩余碳排放量与碳价的关系。可以看出，碳交易价格越高，碳交易对阶梯型碳税的替代效应越小(系统分配于支付碳税的碳排放量占比越大)。系统剩余碳排放量与场景的碳交易价格也呈负相关关系。如图9所示，当碳交易市场的碳价从34.8元/t提高到56.9元/t时，系统剩余碳排放量从7 124.7 t下降到4 326.6 t。算例结果表明通过调整免费碳配额等手段不断提高碳交易市场价格，可以明显增强电力系统的碳减排主观意愿，促使系统逐步降低碳排放量。然而，过高的碳规制强度会增加系统发电成本负担，无法起到合理激励系统碳减排的作用。因此，在实际生产过程中需要完善并推广碳排放权交易机制，适当控制碳交易价格的波动区间，将碳交易价格稳定在合理水平，从而有效平衡系统的减排积极性和经济效益。此外，通过分析系统剩余碳排放量和碳价的关系可知，随着碳价的进一步下降，系统剩余碳排放量的增长逐渐减缓。这表明通过合理运用阶梯型碳税手段，可以避免碳交易价格过低造成碳减排调节作用失灵的风险。

图8 碳排放量分配结果

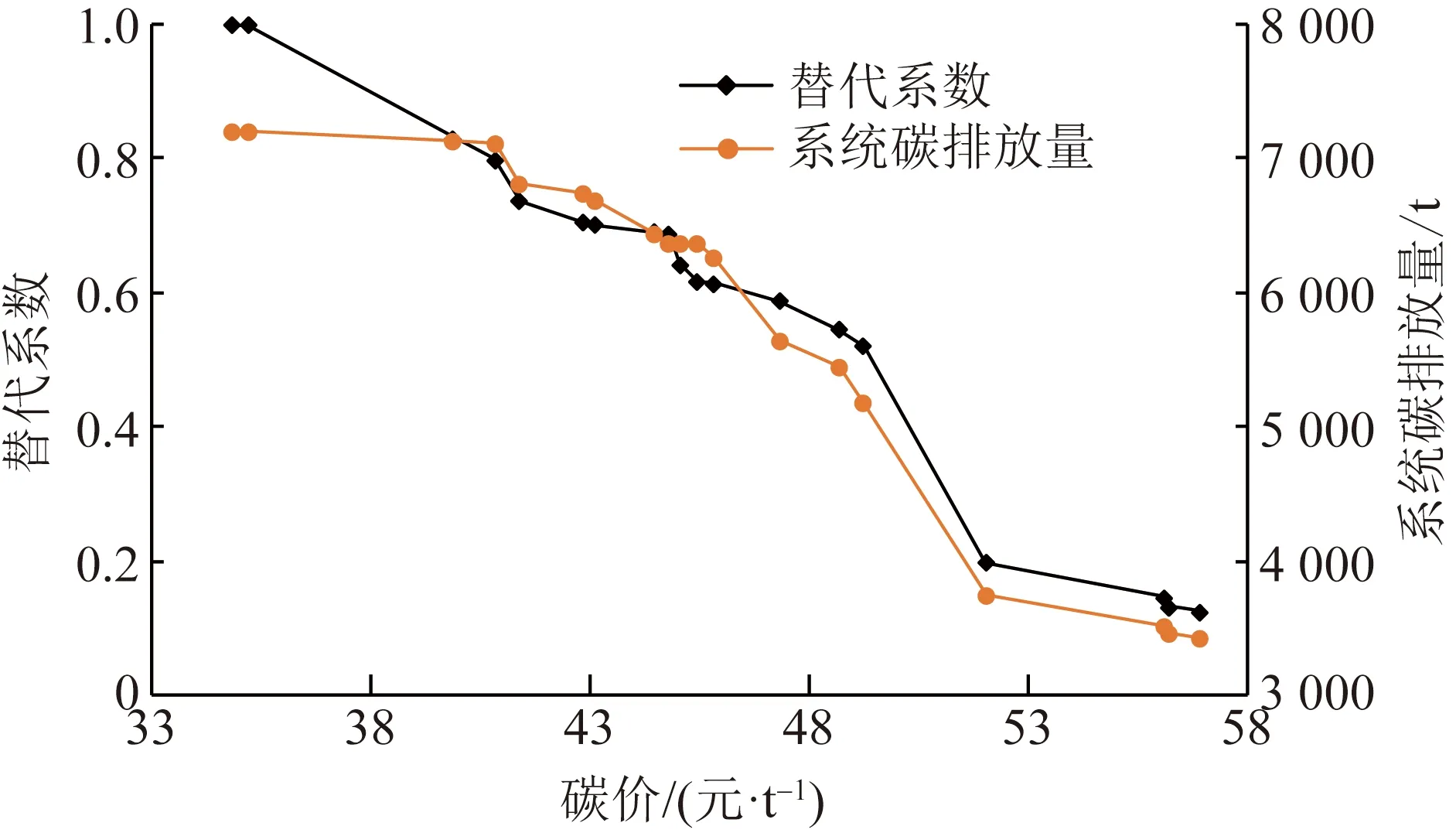
图9 替代系数、碳排放量与碳价关系

4.3 替代效应对模型调度结果的影响

为了说明本文所构建模型考虑阶梯型碳税与波动价格碳交易替代效应对系统低碳调度计划优越性的提高，本节参考其他文献的建模方法，设置了以下4个情景进行对比分析：情景1，采用文献[29]的建模方法，即仅考虑碳交易制的系统低碳经济调度模型；情景2，仅考虑碳税制的系统低碳经济调度模型；情景3，采用文献[30]的建模方法，即考虑阶梯型碳税与碳交易替代效应的系统低碳经济调度模型，忽略碳交易价格波动性；情景4，考虑阶梯型碳税与波动价格碳交易替代效应的系统低碳经济调度模型。

4个情景的系统碳排放量、总运行成本、购电成本以及单位碳排放成本如表1所示。对比前3个情景的调度结果可以得出，相较于情景1和2，情景3在建立阶梯型碳税与碳交易替代效应模型的基础上进行系统低碳经济优化，系统的总运行成本有所下降。算例结果表明，通过对碳税与碳交易替代效应的合理建模，可以有效反映电力系统在复合碳规制影响下的优化决策过程，促使系统灵活协调调度资源。从政策层面上分析，充分认清碳税与碳交易的替代效应，加快建立协调适应的复合碳规制，能够发挥碳税与碳交易之间的优势互补作用，在考虑系统利益诉求的基础上提高系统碳减排的积极性。进一步分析其他调度结果可知，情景3中的单位碳排放成本相比情景2却增加了0.55元/t。这是由于情景3在建模过程中忽略了碳交易价格的不确定性，导致在碳交易价格较高的场景下系统仍将较多的剩余碳排放量分配于购买碳排放许可证，从而增加了调度周期内的碳排放成本。

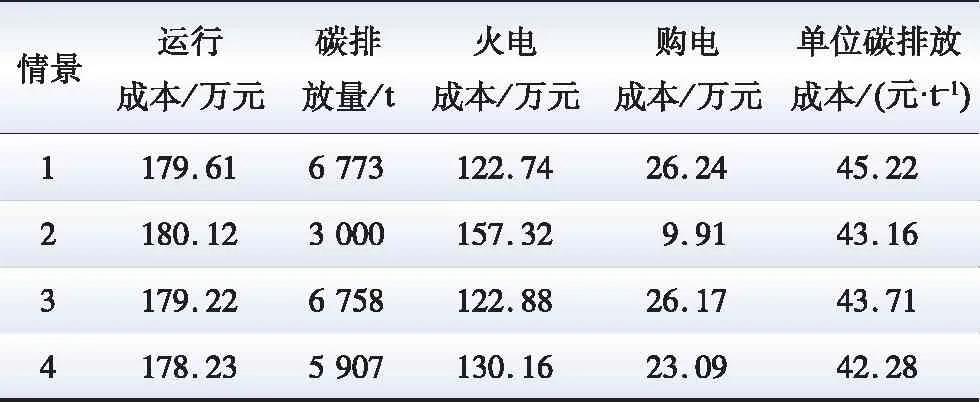
表1 调度结果对比

对比情景3和情景4的调度结果可知，相较于情景3，情景4的运行成本减少了0.99万元，单位碳排放成本减少了1.43元/t，系统的总运行成本和单位碳排放成本均有所降低。考虑碳交易价格的波动特性并采用随机场景法对其进行建模后，系统可以根据当前场景碳交易价格灵活制定购电计划、火电机组出力计划以及碳排放许可证购买计划，降低碳交易价格不确定性对系统经济效益造成的风险，有助于进一步提高系统低碳经济调度计划的有效性和优越性。

4.4 碳捕集设备和储能电站对模型调度结果的影响

为了分析碳捕集设备与储能电站协调优化对模型调度结果的影响，本节在情景4的基础上设置以下4种运行模式进行对比分析：模式1，不考虑碳捕集设备和储能电站；模式2，仅考虑储能电站；模式3，仅考虑碳捕集设备；模式4，考虑碳捕集设备和储能电站进行协调优化。4种运行模式的调度结果对比如表2所示。

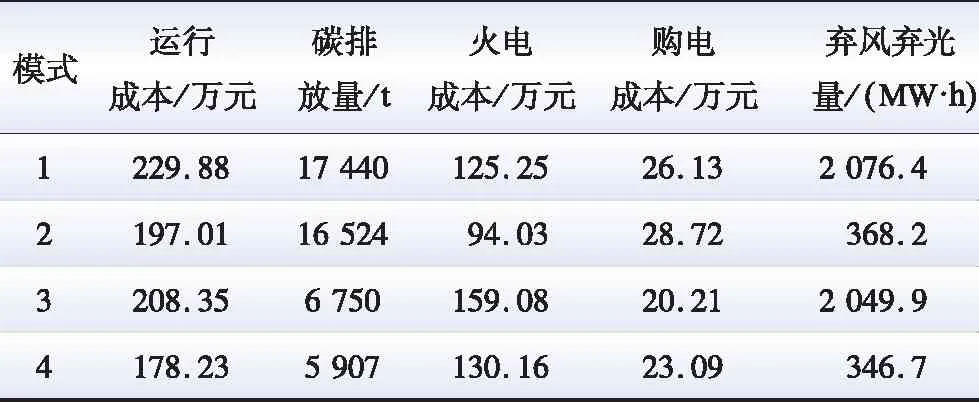
表2 运行模式结果对比

相较于运行模式1和3，模式2和4在风光接入节点同步配置储能电站。对比分析结果表明，储能电站的配置能够有效降低系统的弃风弃光量、碳排放量以及运行成本。一方面，储能电站通过响应购电价格波动，在电价谷时段购入更多电能进行储存，降低系统运行成本。另一方面，储能电站能够缓解风光资源供给与地区负荷需求之间的时间错峰问题，提高可再生能源消纳能力。对比模式1、3以及模式2、4的调度结果可知，运行模式3、4考虑了碳捕集设备的参与后，系统的碳排放量和运行成本均有明显下降。碳捕集设备能够减少高碳火电机组的碳排放量，从源侧实现系统低碳化。此外，模式3和4的弃风弃光量相较于模式1和2分别减少了26.5 MW·h和21.5 MW·h。这表明捕获水平灵活且配置储液罐的碳捕集设备可以实现等同于储能设施的能量时移功能，进一步提升可再生能源的利用率。4种运行模式的调度结果对比分析表明，系统低碳经济调度模型通过碳捕集设备与储能电站的协调优化，可以实现源荷两侧灵活低碳资源的充分利用，有效提升系统运行的经济-环境效益。