控制棒运动对反应堆功率探测器的影响机理研究
2022-06-06杨戴博熊帮平
万 波,黎 刚,李 昆,杨戴博,李 丹,熊帮平
(中国核动力研究设计院 核反应堆系统设计技术重点实验室,成都 610213)
0 引言
在反应堆运行期间,功率监测系统通过布置在堆内或堆外的中子探测器测量中子注量率水平、倍增周期等运行状态参数,实现反应堆运行状态的监测。反应堆功率监测的本质是通过测量反应堆空间内少数几个离散的探测器点位置处的中子注量率情况来表征整个反应堆的功率水平,实现该功能的前提是满足“点堆模型”[1,2]条件,即在反应堆状态监测过程中堆内的中子通量密度分布形状保持不变。然而,在实际工况中可能存在通过移动控制棒棒位调节功率水平的情况,由于控制棒的运动,向堆内局部引入了较大的反应性,这将导致堆内中子通量密度分布形状发生改变(空间效应)[3,4]。如果中子探测器受到空间效应的影响较大,则基于“点堆”假设的反应堆功率监测结果将不能准确地表征实际功率水平。因此,为实现控制棒运动过程中反应堆功率的精确监测,开展反应堆功率监测系统探测器对控制棒运动工况的响应机理的研究很有必要。
针对如何消除反应堆空间效应的问题,国内外研究学者进行过大量研究。文献[5]介绍了一种反应堆物理启动提棒外推临界阶段空间效应的修正方法,通过计算控制棒位于不同深度条件下的归一化中子注量率的差别得到空间效应修正因子,该方法极大地改善了外推曲线的外凸现象。文献[6]研究了一种动态刻棒的新方法,通过求解时空动力学方程推导静态空间因子和动态空间因子,实现了控制棒价值的高精度测量。由此可知,前期关于空间效应消除方法的研究取得了较好的效果,但是这类研究工作主要集中在反应堆物理启堆阶段,所引入的反应性较小,静态、动态空间因子计算过程复杂。另外,没有深入分析反应性引入与中子探测器响应之间的关系,难以实现功率监测探测器的优化布置。因此,对于反应堆功率运行阶段大反应性引入的工况,上述空间效应消除方法是否适用不得而知。
为解决上述难题,本文基于中子输运程序MCNP[7]模拟分析控制棒运动过程中功率监测探测器中子响应函数的变化规律,以及控制棒运动过程中中子通量密度分布形状的变化情况,对比分析控制棒运动引起的空间效应对中子探测器的影响程度,研究结果能够为控制棒运动工况下反应堆功率监测系统的设计提供更多的理论支撑。
1 原理与方法
1.1 KUCA
本 文 以KUCA(Kyoto University Critical Assembly)[8-10]临界装置为对象开展研究工作,该装置中主要包括3 种组件类型,一种是含铀-235 的燃料组件,一种是聚乙烯反射层组件,第3 种是控制棒组件。各组件的排列方式如图1,X 方向和Y 方向上分别布置15 列组件。根据KUCA 装置控制棒组件、反射层组件、燃料组件的几何结构、材料成分、布置方式等信息,通过中子输运程序MCNP 对KUCA 临界装置进行物理建模,准确描述堆芯材料、结构参数。所有控制棒均拔出,通过KCODE 临界源卡计算得到KUCA 装置的系统有效增殖系数keff为1.00109。
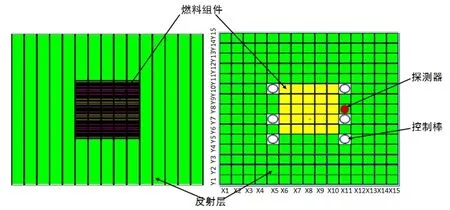
图1 KUCA堆芯结构Fig.1 KUCA Core structure
1.2 探测器中子响应函数
中子探测器的输出计数与探测器位置处的中子通量密度成正比:

其中,R 为探测器计数;φ 为探测器位置处中子通量密度;C 为探测器中子灵敏度系数。堆芯燃料元件裂变反应产生的中子经过慢化、吸收等各种作用之后到达探测器位置处,即中子探测器的读数与堆芯各处的功率有一映射关系,此映射关系即探测器空间响应函数:

其中,P(r)为堆芯位置r 处的中子通量密度(功率);w(r)为中子探测器的空间响应函数,代表r 处一个中子经过各种物理过程之后到达探测器位置处的概率;V 为堆芯体积。
根据公式(2),分别模拟计算堆芯各燃料区域发射的中子到达探测器位置处的计数即可得到中子探测器的响应函数。在推导中子探测器空间响应函数的过程中,裂变中子被作为外中子源进行处理。在由MCNP 开展输运计算时,中子在堆内输运的过程中仍会与堆芯裂变物质发生核裂变反应并释放出中子,通过添加NONU 卡关闭裂变选项,裂变材料俘获吸收中子之后不再发生裂变反应。将KUCA 组件含燃料元件的区域作为中子产生区域,分别单独模拟计算15 根燃料组件出射的中子经过各种物理过程之后到达中子探测器的计数值。在MCNP 模拟程序中,中子源由通用源SDEF 卡定义,采用FM4 计数卡记录探测器输出的中子计数。
2 结果与讨论
2.1 中子响应函数
采用1.2 节介绍的方法,模拟计算X11Y7 位置处控制棒分别位于堆芯外部、一半插入堆内以及完全插入堆内3 种情况下的探测器中子响应函数,得到控制棒插入堆芯一半和完全插入堆芯后探测器中子响应函数的变化情况如图3。对比图2(a)和图2(b)可知,控制棒完全插入引起的中子响应函数变化程度比控制棒只插入一半更显著。对于每一列燃料组件X6 ~X11,Y6 到Y11 方向,随着控制棒的插入,探测器的中子响应函数的下降程度逐渐增大,且Y9 和Y10 组件位置处的下降最为明显。这是因为控制棒空间上位于Y9、Y10 组件和中子探测器之间,因此,Y9、Y10 组件位置处发射的中子达到探测器的过程中还会受到控制棒吸收的影响,且与Y6、Y7 组件发射的中子比起来,Y9、Y10 组件受到控制棒的屏蔽效应更明显。对于X6、X7 和X8 这3 列燃料组件,控制棒插入前后中子响应函数的变化均较小,这是因为这一区域离控制棒的位置相对较远,控制棒的插入对这一区域出射中子的吸收效应不明显。从以上有关中子响应函数的计算结果可知,控制棒插入之后堆芯不同区域组件发射的中子到达探测器位置处的概率也将发生改变,且变化程度各不相同,因此在通过探测器监测堆芯中子注量率水平时,需要考虑中子响应函数的变化对于测量精度的影响。
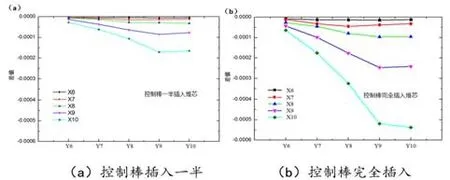
图2 中子响应函数变化情况Fig.2 Variation of neutron response function
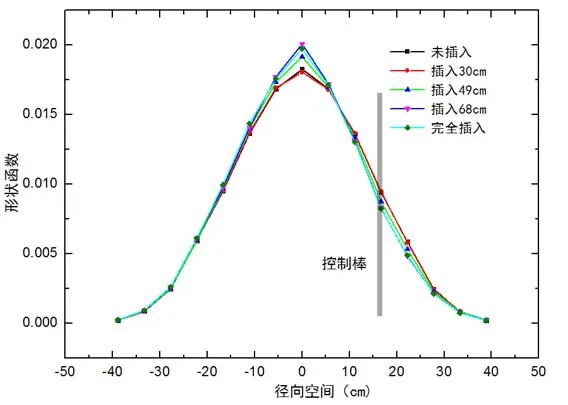
图3 控制棒插入堆芯不同深度条件下堆芯中子通量密度分布形状函数Fig.3 Shape function of core neutron flux density distribution under different depths of control rods inserted into the core
2.2 中子分布形状函数
在由中子输运理论推导点反应堆动力学假设的过程中,假设中子通量密度分布可以分解成通量分布形状函数φ(r,E,t)以及一个幅度因子n(t)的乘积,如公式(3)所示:

根据公式(3),中子通量分布形状函数φ(r,E,t)可以看作归一化的中子通量密度分布。分别模拟计算控制棒位于堆芯外部、插入堆芯30cm、插入堆芯49cm、插入堆芯68cm 以及完全插入堆芯等5 种堆芯结构下KUCA 装置的中子通量密度分布情况,统计Y8 各组件的中子通量密度,并根据公式(3)计算Y8 各组件位置处的中子通量密度分布形状函数。中子通量密度分布形状函数见图3。
从图3 中可以看出,单根控制棒插入堆芯不同深度,堆芯内的中子通量密度分布形状函数将发生改变。控制棒插入位置附近,随着控制棒插入,中子通量密度分布形状函数的变化比较明显;对于远离控制棒插入位置的区域,控制棒不同插入深度情况下中子通量密度分布形状函数基本没有变化,即控制棒的运动对这一区域的中子通量密度分布形状影响很小。X=0 位置处的中子通量密度形状函数的变化也比较明显,这是因为采用通用源卡SDEF 开展中子输运计算时的中子源位置设定在此处,且X8Y8 燃料组件上部被掏空,导致这一区域中子泄漏程度更大,中子通量密度分布形状函数更加复杂。因此,在开展反应堆功率水平监测时,如果探测器布置在控制棒附近,则需要考虑中子通量密度分布形状函数变化对于监测结果准确性的干扰。
图4给出了控制棒插入堆芯过程中,探测器位置处的中子通量密度形状函数与探测器响应函数随控制棒棒位的变化情况。计算结果显示,由于控制棒的插入,探测器位置处的中子通量形状函数与探测器响应函数均明显下降,且下降趋势基本一致。
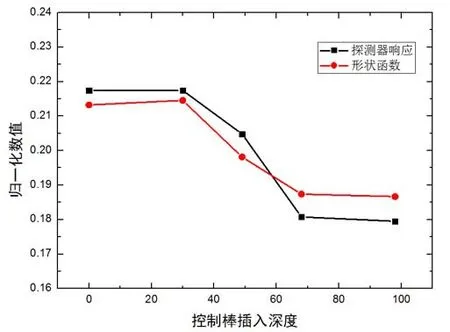
图4 形状函数与探测器响应随控制棒插入位置的变化情况Fig.4 Variation of shape function and detector response with control rod insertion position
2.3 空间效应修正
反应堆功率水平监测的理论公式如式(4)所示:

其中,P(t)代表t 时刻反应堆功率;I(t)为探测器电流信号;K 为固定参数。探测器电流信号与功率水平成正比,通过实时测量探测器的电流信号即可实现反应堆功率的监测。公式(4)本质是通过探测器位置处的中子通量密度的测量来反映整个反应堆的中子注量率水平,将反应堆视作一个点,不考虑堆芯中子通量密度分布形状的改变。由于控制棒的引入引起反应堆内中子通量密度分布形状函数的改变,直接使用公式(4)进行反应堆功率水平的监测将产生较大误差,功率监测结果随探测器位置的不同也将产生明显区别。
假设控制棒插入堆芯前探测器位置处的中子通量密度为φ0,中子注量率水平为n0,中子通量密度形状分布函数为φ0;控制棒插入之后探测器位置处的中子通量密度为φ1,中子注量率水平为n1,中子通量密度形状分布函数为φ1。可以推导得到控制棒插入前后堆芯总的中子注量率变化情况:
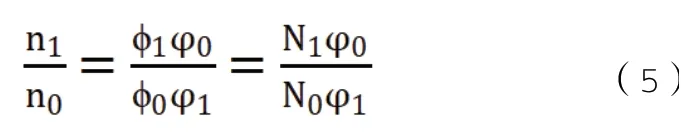
其中,N0和N1分别为控制棒插入前后探测器输出的中子计数(电流),与探测器位置处的中子通量密度成正比。由公式(5)可以看出,如果控制棒插入前后堆芯中子通量密度分布形状函数φ1和φ1没有发生变化,则堆芯总中子注量率水平的变化情况与探测器实际探测到的中子计数(电流)相同。定义控制棒插入前后堆芯中子通量密度分布形状函数的比值为空间修正因子,用于描述控制棒插入前后堆芯中子通量密度分布形状函数的差异:

空间修正因子f 越接近1,中子通量密度分布形状函数的变化越不明显。考虑形状函数的变化之后公式(5)可以描述为:

控制棒插入堆芯之后,探测器的中子计数还需要再乘上一个修正因子f 才能正确表征堆芯总中子注量率水平的变化情况。因此,为实现堆芯中子注量率(功率)水平的准确监测,公式(4)应修正为:

3 结论
本文以零功率反应堆装置KUCA 为研究对象,通过中子输运程序MCNP 对其进行物理建模,模拟研究了控制棒插入堆芯前后探测器对各个燃料组件的中子响应函数的变化情况以及堆芯中子通量密度分布形状函数的变化规律。研究结果表明控制棒插入堆芯之后,由于控制棒的屏蔽效应,中子探测器-控制棒外延线区域燃料组件的中子响应函数下降明显,且靠近控制棒区域的响应函数下降最大。由于控制棒的插入,探测器位置处的中子通量形状函数与探测器响应函数均明显下降,且下降趋势基本一致。最后,引入空间效应修正因子对反应堆功率监测理论公式进行修正以减少控制棒插入过程中功率监测的误差。研究结果为反应堆功率监测探测器的合理布局提供了一定依据,同时为局部反应性引入条件下反应堆功率监测精度的提升具有参考价值。
