基于GTWRK的PM2.5浓度空间插值方法
2022-06-06谢劭峰潘梦清黄良珂刘立龙
谢劭峰,张 伟,潘梦清,黄良珂*,刘立龙
(1.桂林理工大学 测绘地理信息学院,广西 桂林 541006;2.河南省地震局 鹤壁地震监测中心站,河南 鹤壁 456200;3.桂林市测绘研究院,广西 桂林 541002)
0 引言
随着我国经济的快速发展和城市化进程的加快,大气细颗粒物PM2.5已经成为影响我国大气环境污染的主要因素之一[1]。目前PM2.5的监测以定点的地面监测为主,由于监测站点分散,仅能观测有限空间范围内的空气污染情况,无法获取区域内连续的PM2.5空间分布格局[2]。
为了获取连续的PM2.5空间分布,文献[3-5]采用克里金方法进行PM2.5浓度空间插值。然而由于PM2.5具有很强的空间异质性,因此仅仅依靠普通克里金插值获得PM2.5空间分布,效果不太理想[2]。地理加权回归(Geographically Weighted Regression,GWR)模型[6-8]可以在一定程度上解决PM2.5浓度估算的空间异质性问题,但常规GWR模型忽略了时间非平稳性的影响。针对这个问题,文献[9-11]将时间因素加入到GWR模型中,采用时空地理加权回归(Geographically and Temporally Weighted Regression,GTWR)方法研究PM2.5浓度的时空分布。尽管GTWR模型具有较高的拟合优度,但GTWR模型难以解决PM2.5分布的复杂非线性问题,对回归残差也未进行进一步的处理。
土地利用回归(Land Use Regression,LUR)模型是PM2.5时空分布模拟的有效方法。文献[12-14]基于PM2.5浓度与土地利用、地形、气候、交通和人口密度等因素之间的相关关系,使用LUR模型对PM2.5浓度的空间分布进行反演,较好地反映了区域PM2.5浓度分布情况,但LUR模型难以解决PM2.5分布的时空非平稳性问题。还有研究人员采用机器学习方法进行PM2.5浓度预测或反演:文献[15]采用随机森林方法估计PM2.5浓度;文献[16]基于气溶胶光学厚度(Aerosol Optical Depth,AOD)产品和气象再分析资料,采用随机森林等方法反演北京市近地面PM2.5浓度;文献[17]利用卷积神经网络预报模型进行京津冀区域PM2.5浓度预报;文献[18]构建了基于卷积神经网络和长短时记忆的深度学习预报模型。这些机器学习方法也取得了较好的预测结果,但同样无法有效处理PM2.5时空分布的非平稳性问题。
上述研究基于不同方法、不同数据进行区域PM2.5浓度预测或模拟,取得了较好的效果。但这些方法难以同时有效处理PM2.5分布的时空非平稳性、空间自相关性问题。因此,本文基于GTWR方法处理时空非平稳性问题和克里金方法处理空间自相关性问题的良好能力,建立了顾及多元因子影响的时空地理加权回归克里金(Geographically and Temporally Weighted Regression Kriging,GTWRK)模型,进行广西PM2.5浓度预测,并对比分析了模型的预测精度,绘制了2015—2019年广西PM2.5浓度空间分布图。
1 数据与方法
1.1 研究区概况
广西地处中国华南地区西部,位于20°54′~26°24′N、104°26′~112°04′E,陆地总面积约23.67万平方千米,南濒热带海洋,北为南岭山地,西延云贵高原,境内河流纵横,地理环境比较复杂。广西气候类型多样,夏长冬短,年均温在16~23 ℃。从全国来看,尽管广西不是雾霾高发地区,但部分地市出现雾霾的天数比较高,尤其是梧州、桂林和柳州3市雾霾天数出现的频率超过20%[19]。
1.2 数据来源及预处理
PM2.5浓度数据来源于中国环境监测总站(http:∥www.cnemc.cn/),时间跨度为2015年1月1日—2019年12月31日。得到的数据为逐时监测的站点数据,在计算得到日均值的基础上进一步得到建模使用的月均值和年均值。
气象数据来源于中国气象数据网(http:∥data.cma.cn/),获取的数据主要包括降水量(Precipitation,PRE)、风速(Wind Speed,WS)、气压(Pressure,PRS)、温度(Temperature,TEM)、相对湿度(Relative humidity,RHU)和水汽压(Vapor Pressure,VP)。
由于气象站点和空气质量监测站点的空间位置不同且数量也不同,本文对气象数据进行反距离加权插值(Inverse Distance Weighting,IDW)到空气质量监测站点位置处。气象站点共有17个,其中百色市有3个,河池市、柳州市和来宾市各有2个,桂林市、贺州市、梧州市、玉林市、钦州市、南宁市、防城港市和崇左市各有1个。空气质量监测站点共有50个,其中南宁市有8个,柳州市有6个,桂林市、梧州市、贵港市和北海市各有4个,河池市、钦州市、防城港市和玉林市各有3个,百色市、崇左市、贺州市和来宾市各有2个。
AOD数据来源于美国国家航天局(https:∥ladsweb.modaps.eosdis.nasa.gov/),数据为MCD19A2,空间分辨率为1 km,时间分辨率为1 d。
全球导航卫星系统(Global Navigation Satellite System,GNSS)天顶对流层延迟(Zenith Tropospheric Delay,ZTD)数据来源于中国地震局GNSS数据产品服务平台(ftp:∥ftp.cgps.ac.cn/products)。由于陆态网在广西仅有6个基准站,为了便于研究,本文将与广西相邻(包括湖南、云南、贵州、广东和海南)的共计44个GNSS基准站的ZTD数据分月份对广西进行反距离加权插值,最后得到广西空气质量监测站点月均的ZTD值。
高程数据(Digital Elevation Model,DEM)来源于中国科学院地理科学与资源研究所(http:∥www.resdc.cn/Default.aspx);植被指数(Normalized Difference Vegetation Index,NDVI)来源于美国国家航天局(https:∥ladsweb.modaps.eosdis.nasa.gov/);人口数据来源于Worldpop网站(https:∥www.worldpop.org/)发布的1 km的栅格数据集,时间范围为2015—2019年。
由于AOD数据的空间分辨率为1 km×1 km,所以将所有数据全部转化成相同的空间分辨率。为了保持所有数据的空间范围一致,本文将所有栅格数据集的坐标系都转化为CGCS2000-Alberts投影坐标系,用以准确获得空气质量监测站点上的各个特征变量。
1.3 研究方法
1.3.1 地理加权回归
GWR是一种改进的空间线性回归模型,其系数不是固定的,而是随着空间位置变化,并且将局部特征作为权重。GWR模型可以表示为[20]:
(1)
式中,yi为在位置i处的因变量值;xik(k=1,2,…,p)为位置i处的自变量值;(ui,νi)为回归分析点i的坐标;β0(ui,νi)为截距项;βk(ui,νi) (k=1,2,…,p)为回归系数;εi为回归残差。
GWR模型的回归系数采用加权最小二乘法求解[20]:
(2)
式中,W(ui,νi)为m×m的空间权重对角矩阵;X为m×(n+1)自变量的设计矩阵;Y为m×1因变量向量。
空间权重采用Bi-square函数计算[20]:
(3)
式中,wij为空间已知点j去估计未知点i时的权重;dij为点i与j之间的欧氏距离;h为带宽。
带宽采用最小AICc准则(corrected Akaike Information Criterion)进行判断[20]:
AICc=-nln(σ′)+nln(2π)+
n{[n+tr(S)]/[n-2-tr(S)]},
(4)
式中,n为数据点的数量;σ′为误差项(估计标准偏差);tr(S)为帽子矩阵S的迹,是带宽h的函数。
1.3.2 时空地理加权回归
将时间效应整合到GWR模型中,就成为了GTWR模型,可以用来同时处理时间和空间非平稳问题。GTWR可以表示为[11]:
(5)
式中,(ui,vi,ti)为第i个样本点的时空坐标。
与GWR模型相似,回归系数采用加权最小二乘法求解:
(6)
引入时空权重矩阵W(ui,νi,ti)来衡量样本i在估计样本j方面相对于时间和空间的权重。时空距离dST为空间距离dS与时间距离dT的线性组合[11]:
(7)
式中,ti和tj为观测时间i和j;λ和μ为用于协调空间距离和时间之间不同单位的影响权重。
1.3.3 克里金法
克里金(Kriging)插值是建立在变异函数理论及结构分析基础上,利用区域化变量的原始数据和变异函数的结构性,对未知点区域化变量的取值进行线性无偏最优估计的一种方法。克里金法是一种空间局部插值方法,适用于具有空间相关性的区域化变量研究。克里金插值可表示为[20]:
(8)
式中,z*(x0)为插值点x0处的估计值;z(xi)为n个样本点中xi处的观测值;λi为对应的权重。
1.3.4 时空地理加权回归克里金
GTWRK是在GTWR的基础上,对其回归残差进行普通克里金(Ordinary Kriging,OK)插值,最后将OK残差插值结果和GTWR预测值相加而得。GTWRK可表示为:
yGTWRK(μi,νi,ti)=yGTWR(μi,νi,ti)+εOK(μi,νi,ti),
(9)
式中,yGTWRK(μi,νi,ti)为GTWRK的预测值;yGTWR(μi,νi,ti)为GTWR的预测值;εOK(μi,νi,ti)为GTWR回归残差进行普通克里金插值的结果。
2 模型构建与精度评估
2.1 相关性分析与特征变量选择
为了研究广西地区影响PM2.5浓度变化的因素,根据相关研究选择气象数据(包括降水量(PRE)、风速(WS)、气压(PRS)、温度(TEM)、相对湿度(RHU)和水汽压(VP))、高程数据(DEM)、气溶胶数据(AOD)、人口密度(POP)、植被指数(NDVI)和GNSS ZTD数据为特征变量,使用SPSS软件的双变量分析功能分析各个特征变量与PM2.5浓度之间的相关性,结果如表1所示。

表1 各变量与PM2.5浓度的相关性
从表1可知,NDVI,PRS,DEM与PM2.5浓度的相关性不显著;AOD,POP与PM2.5浓度呈显著正相关,AOD的相关系数达0.37;PRE,WS,TEM,RHU,VP,ZTD与PM2.5浓度呈显著负相关,其中VP的相关系数达-0.74。
然而,并不是所有相关性显著的变量都适用于GTWRK模型的建模预测,因此这些变量还需要经过共线性诊断。方差膨胀因子(Variance Inflation Factor,VIF)诊断法常用来检验各个变量之间是否存在多重共线性。VIF值越大,变量之间的多重共线性越大。本文以7.5为界限,VIF值高于7.5的变量可以判断为存在共线性的变量。
为了检验变量之间的共线性,以相关性较高的变量为自变量、PM2.5浓度为因变量,在ArcGIS中进行普通最小二乘(Ordinary Least Square,OLS)建模,OLS建模结果能够检验出变量之间是否存在共线性。剔除共线性较高的变量前、后结果分别如表2和表3所示。
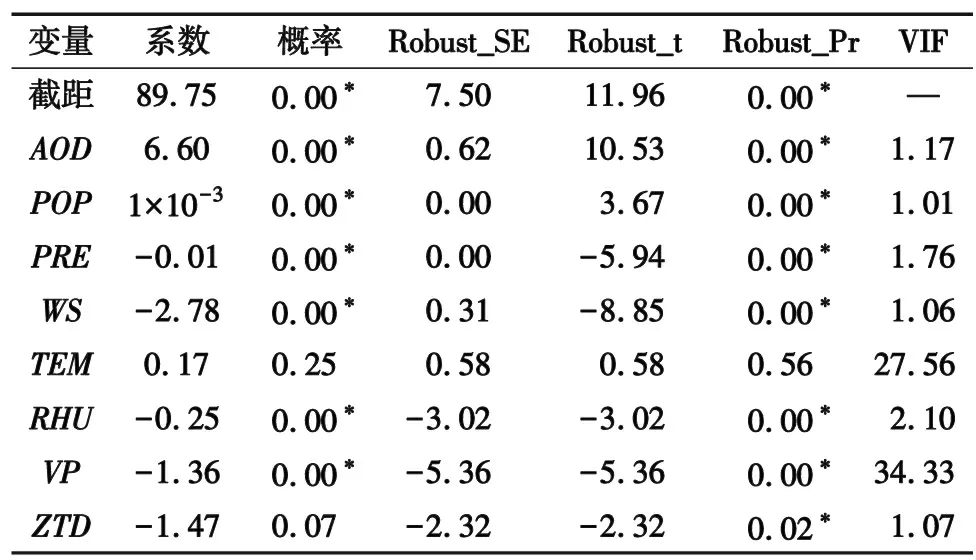
表2 剔除变量前OLS的建模结果
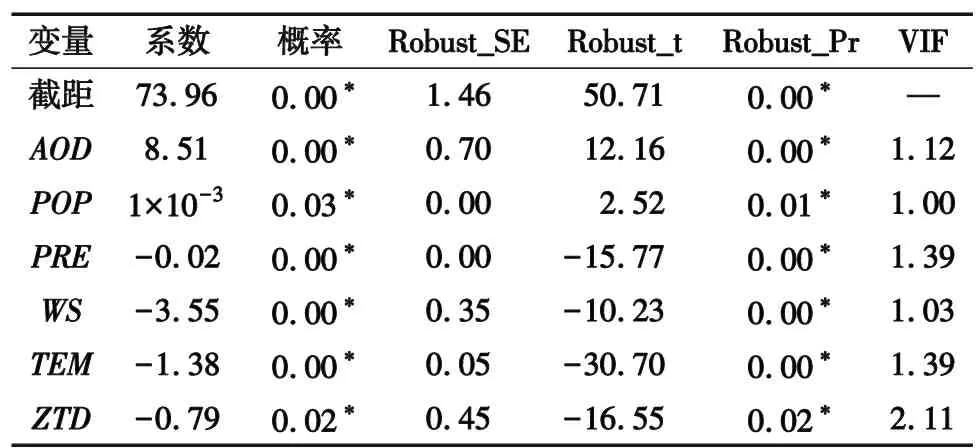
表3 剔除变量后OLS的建模结果
由表2和表3可知,剔除共线性较高的变量后各变量的VIF值均小于7.5,说明变量之间已经不存在多重共线性,表3中所有变量可以用来建模。变量系数的正负也反映了变量对PM2.5浓度的影响方向,AOD和POP与PM2.5浓度呈正相关,PRE,WS,TEM和ZTD与PM2.5浓度呈负相关,与上述的皮尔逊相关系数分析的影响方向相同,且变量系数的大小也说明了对PM2.5浓度影响的强弱关系。从表3还可以看出,对PM2.5浓度正向影响较大的是AOD,负向影响较大的是WS。
2.2 模型构建
GWR模型在ArcGIS软件工具箱里空间关系建模中的地理加权回归模块实现,GTWR模型在ArcGIS软件的GTWR插件实现。将POP,AOD,PRE,WS,TEM和ZTD选为解释变量,PM2.5选为因变量。2个模型的建模结果如表4所示。
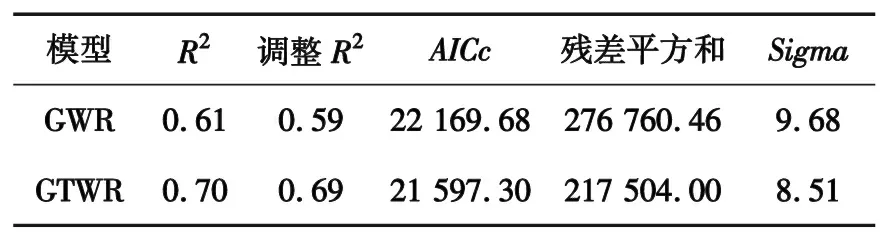
表4 GWR和GTWR模型建模结果
表4中的R2表示拟合优度,值范围0~1,值越接近于0模型拟合越差,反之表明模型的拟合效果越好。一般情况下,模型参考的是调整后的R2,GTWR模型调整后的R2更接近1,说明GTWR模型拟合效果更好;GTWR模型的AICc的值比GWR模型小,说明GTWR模型比GWR模型更优;GTWR模型的残差平方和明显小于GWR模型的残差平方和;Sigma表示剩余平方和除以残差的有效自由度的平方根,该统计值越小越好,表中的GTWR模型的Sigma值也小于GWR模型。综上,GTWR模型结果的各项参数均优于GWR模型,说明GTWR模型更适用于PM2.5浓度预测。
2.3 精度评估
为了检验模型的预测精度,随机选择了80%的站点数据进行训练,20%的站点数据进行验证。为了保证所选择的训练样本和验证样本的科学性,根据均匀分布原则选取建模样本和验证样本,即每个月选择了不同城市的不同站点作为训练集和验证集。
为了验证模型的预测精度,采用平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)和决定系数(R2)3个指标来评价各个模型的预测精度,结果如表5所示。

表5 模型精度对比
从表5可知,加入时间效应的GTWR模型和GTWRK模型优于对应的未加入时间效应的GWR模型和GWRK模型;残差经过克里金插值修正后预测精度优于未进行残差修正的模型;GTWRK模型的各项评价指标均优于其他模型,表明GTWRK比其他模型具有更好的预测精度。
用Matlab软件绘制4个模型的实测PM2.5浓度与预测PM2.5浓度的散点图,如图1所示。由图1可知,相比于其他模型,GTWRK模型的预测与实测散点图更接近于一条直线,该模型的R2=0.814,说明实测浓度与预测浓度拟合程度高,预测值更接近实测值,进一步证明了GTWRK模型的预测能力。

(a) GWR模型

(b) GTWR模型

(c) GWRK模型
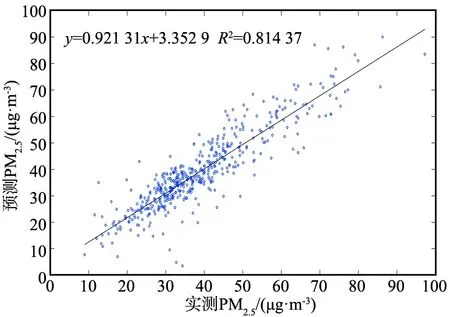
(d) GTWRK模型
3 广西PM2.5浓度空间分布特征
为了直观地显示广西PM2.5浓度的时空分布特征,利用ArcGIS中的栅格计算器功能,以年为时间尺度进行PM2.5浓度年均值计算,将GTWRK模型的PM2.5浓度预测结果进行空间化表达,得到2015—2019年广西PM2.5浓度的空间分布,结果如图2所示。

(a) 2015年
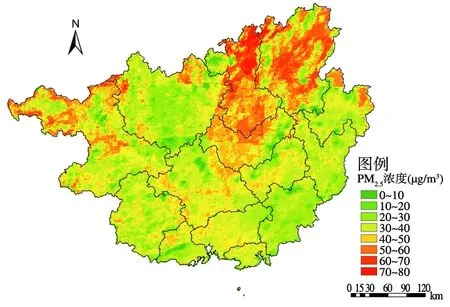
(b) 2016年
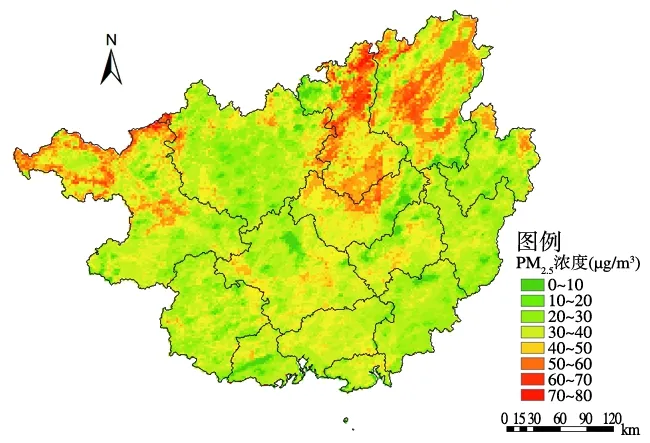
(c) 2017年

(d) 2018年

(e) 2019年
由图2可知,2015年高浓度PM2.5主要分布在百色、柳州和桂林,其他地区PM2.5浓度相对较低。2016年高浓度PM2.5主要分布在柳州和桂林,百色的高浓度PM2.5分布面积减少。2017年高浓度PM2.5主要分布在柳州和桂林,但是分布面积较上年有所减少。2018年高浓度PM2.5分布面积明显减少,主要还是集中在柳州和桂林;来宾较上年有所增加。2019年高浓度PM2.5主要位于柳州、桂林、来宾,但高浓度PM2.5分布面积显著减少;防城港、北海、钦州、崇左、南宁、河池等市PM2.5浓度较低。总体来看,2015—2019年广西高浓度PM2.5主要位于柳州和桂林,但分布面积逐年减少,说明广西环境治理初见成效。
4 结束语
通过构建顾及多因子影响的GTWRK模型进行PM2.5浓度预测和空间分布制图,得到以下结论:
① 广西地区影响PM2.5浓度变化显著性较高的变量有AOD,POP,PRE,WS,TEM,RHU,VP和ZTD,正向影响最大的变量是AOD,负向影响最大的变量是VP。
② GTWRK模型更适用于区域PM2.5浓度预测,其预测结果的MAE,RMSE,R2分别为4.69 μg/m3,6.44 μg/m3,0.81,全部优于GWR,GWRK,GTWR,GTWRK模型。
③ 2015—2019年广西高浓度PM2.5分布面积逐年递减,2015年分布面积最大,2019年分布面积最小;高浓度PM2.5主要分布在桂林和柳州,低浓度主要分布于防城港和北海。
由于本文气象参数和ZTD等数据获取站点数量不一,只能通过插值法进行区域数据获取,因此精度还可以进一步优化。
