基于介电测井和电阻率测井的致密砂岩储层饱和度联合反演方法

2022-06-06赵培强陈阵李卫兵毛志强柯式镇王海朋

测井技术 2022年2期

赵培强,陈阵,李卫兵,毛志强,柯式镇,王海朋

(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京102249;2.中国石油大学(北京)地球探测与信息技术北京市重点实验室,北京102249;3.中国石油长庆油田公司勘探开发研究院,陕西西安710018;4.中国石油集团测井有限公司辽河分公司,辽宁盘锦124010)

0 引言

含油饱和度是致密砂岩储层表征和储量计算的重要参数之一[1-2]。鄂尔多斯盆地三叠系延长组长71段、长72段及长8段具有丰富的致密油藏[3-4],由于其地层水矿化度变化较大、孔隙结构复杂、泥质含量较高[5-6],使得含油饱和度的评价较为困难。尤其是地层水矿化度变化大[5],确定地层水电阻率难度大,利用电阻率测井资料评价饱和度遇到很大挑战。除电阻率测井资料之外,介电测井资料也用于储层含油饱和度的计算[7]。介电测井仪器特别是斯伦贝谢公司的阵列介电测井仪器(Array Dielectric Tool,ADT)可提供兆赫兹频段的介电频散曲线,这些曲线蕴含丰富的地层信息[8]。由于非常规致密砂岩储层岩石致密,大多数情况下钻井液侵入较浅,相对于常规油气储层而言,介电测井在非常规油气储层饱和度评价中具有较大优势。

近年来,介电测井在国外(尤其是北美地区)非常规油气储层饱和度评价中应用广泛。如Seleznev等[9]、Musharfi等[10]、Almarzooq等[11]、Chen等[12]基于复折射率(Complex Refractive Index Method,CRIM)模型[13],利用频率为1 GHz的相对介电常数计算不同地区的非常规油气储层饱和度。Han等[14]基于Lichtenecker-Rother模型[15]、Stroud-Milton-De(SMD)模型[16]和Clay-Pyrite Interfacial-Polarization(IP)模型[17]利用多频率介电测井信息计算美国Bakken页岩储层参数。Tathed等[18-19]联合SMD模型、CRIM模型和Waxman-Smith模型[20],利用多频率的复介电常数结合电阻率曲线对美国Bakken、Wolfcamp页岩储层饱和度进行反演计算[18-20]。Han等[21]基于IP模型利用宽频电频散数据评估下古生界富有机质页岩的饱和度等参数。这些学者充分利用介电测井资料,取得了较好的应用效果。然而,介电测井资料在中国非常规油气储层的应用研究还相对较少。Zhao等[22]和Guo等[6]基于仿阿尔奇公式利用在1 GHz频率时测量的相对介电常数,分别开展了准噶尔盆地二叠系芦草沟组致密油储层和鄂尔多斯盆地三叠系延长组长8段致密砂岩储层饱和度计算研究。Zhao等[8]基于泥质砂岩模型和CRIM模型,利用多频率的复介电常数开展鄂尔多斯盆地页岩储层饱和度评价研究。但是尚未见到多频率复介电常数在中国致密砂岩储层饱和度评价的应用,亟需探索介电频散模型在国内致密砂岩储层的适用性,并提供准确的储层信息。

本文以鄂尔多斯盆地三叠系延长组致密砂岩储层为研究对象,基于泥质砂岩介电频散模型、复折射率模型和西门杜电阻率模型,利用全局优化粒子群算法处理介电测井和阵列感应测井曲线,计算含水饱和度、水相曲折度指数、冲洗带矿化度和泥质频散项体积含量。反演结果经过理论合成测井响应、岩心分析数据及试油数据的验证,证实了本文方法的有效性和准确性。

1 储层岩石介电测井和电阻率测井响应模型

1.1 地层水介电测井响应模型

地层水的复介电常数由实部和虚部组成,其表达式为[16]

(1)

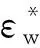
地层水的相对介电常数εrw和直流电导率σw均为储层温度和地层水矿化度的函数,本文采用式(2)、式(3)和式(4)计算[16]

εrw(0,T)=94.88-0.2317T+0.000217T2

(2)

(3)

(4)

式中,T为地层温度,℉;Sal为矿化度,g/L。式(4)是根据斯伦贝谢公司的地层水电阻率与矿化度关系图版而获得。

1.2 岩石介电测井响应模型

复折射率(CRIM)模型是解释频率为1 GHz左右的介电常数的常用模型,由于在1 GHz频率下的界面极化效应基本可以忽略不计,而界面极化与岩石结构相关,故该模型不包括岩石结构的变化。包含3种介质的CRIM模型为[7,13]

(5)

式中,ε*为岩石的复介电常数;φ为岩石的总孔隙度,%;Sw为含水饱和度,%;εm和εh分别为岩石和油气的相对介电常数。

Stroud等[16]1986年提出一种考虑介电频散的纯岩石饱和流体模型,称为“SMD模型”。该模型利用岩石总孔隙度、流体饱和度、岩石骨架相对介电常数及岩石结构指数等参数,计算饱和流体岩石兆赫兹频段下的复介电常数及其频散曲线,反过来可根据岩石复介电常数及频散曲线反演岩石流体饱和度,SMD模型表达式为[16]

(6)

(7)

式中,MN为水相曲折度指数;Γ为伽马函数;εrm为岩石骨架和油气的混合介电常数;εm和εh分别为岩石骨架和油气的相对介电常数。

(8)

式中,εt为频散项的高频相对介电常数,设置为干黏土介电常数;σd为黏土束缚水的电导率,S/m;fc为临界频率,大约200 MHz;εs为频散相的低频相对介电常数,它应该足够高,以表征黏土表面效应的频散性质。

φw=φSw

(9)

式中,φw为含水孔隙度,%;pd为泥质频散项体积含量,V/V,用于量化频散相,表征额外的黏土诱导效应对总频散的贡献。最后,将复合导电相代入SMD模型中,提出一种新的泥质砂岩模型[23]

(10)

1.3 泥质砂岩电导模型

鄂尔多斯盆地三叠系延长组致密砂岩储层泥质含量较多,利用经典纯砂岩阿尔奇公式将使得计算结果产生一定误差,需要采用泥质砂岩电导率模型。斯伦贝谢公司常用的西门杜方程,不考虑泥质的分布形式,具有较好的应用效果,西门杜方程可表示为[24]

(11)

式中,Rt为原状地层电阻率,Ω·m;Vsh为泥质含量,%;Rsh为泥岩电阻率,Ω·m;Rw为地层水电阻率,Ω·m;a为阿尔奇公式指数,通常为1;n为饱和度指数;m为胶结指数。

介电测井探测深度相对较浅,可采用探测深度较浅的电阻率曲线与其匹配

(12)

式中,Rxo为冲洗带地层电阻率,Ω·m;Sxo为冲洗带地层含水饱和度,%;Rmf为冲洗带流体电阻率,Ω·m,与式(4)中电导率互为倒数。

该研究中,最高频率的介电常数和电导率曲线采用CRIM模型处理,其他3种频率的介电常数和电导率采用泥质砂岩模型处理,选择阵列感应测井10 in(非法定计量单位,1 in=2.54 cm,下同)的探测深度曲线作为Rxo电阻率曲线。

2 基于粒子群算法的参数反演

联立上述3种模型,构建最小平方目标函数

(13)

式中,F为目标函数;εlog,j为介电测井实际测量的相对介电常数;σlog,j为实际测量的电导率,S/m;j=1,2,3,4,分别表示4个频率;Rlog为电阻率测井实测值,Ω·m;εcal,j为参数反演过程中利用式(5)和式(10)计算的理论相对介电常数;σcal,j为参数反演过程中利用式(5)和式(10)计算的理论电导率,S/m;Rcal为参数反演过程中利用式(12)计算的理论电阻率,Ω·m。

由于各模型的响应方程为明显的非线性方程,为避免反演参数时陷入局部最优解,本文采用全局最优反演算法即粒子群算法(Particle Swarm Optimization,PSO)进行反演。PSO算法由Eberhart和Kennedy提出[25],其基本思路是将优化问题的每个解视为1个代表人工鸟的粒子,每个粒子都有自己的位置和速度,并根据一定的法则调整位置和速度,整体飞向最优目标[26-27]。粒子的速度变化主要由粒子前一次迭代的速度、个体最佳适应值位置和种群最佳适应值位置所决定,粒子的速度和位置迭代公式分别为[28-30]

Vl,r+1=WdVl,r+b1c1(pBest,l,r-Xl,r)+

b2c2(gBest,r-Xl,r)

(14)

Xl,r+1=Xl,r+Vl,r+1

(15)

式中,Vl,r为第l个粒子在第r次迭代的速度;Xl,r为第l个粒子在第r次迭代的位置;Wd为指数衰减的惯性权重系数;pBest,l,r为寻优过程中,迭代至第r次为止第l个粒子最佳适应值的位置;gBest,r为粒子群迭代至第r次最优适应值的位置;b1和b2为2个随机函数值,取0～1间的随机数增加寻优过程的随机性;c1和c2为学习因子。

本文假设MN=m=n,输入的参数包括4组不同频率的相对介电常数、电导率、阵列感应测井电阻率、孔隙度、油的相对介电常数、地层温度和岩石骨架相对介电常数;反演参数包括含水饱和度Sw(默认Sw等于Sxo)、水相曲折度指数MN、冲洗带矿化度Sal和泥质频散项体积含量pd。计算流程如图1所示。

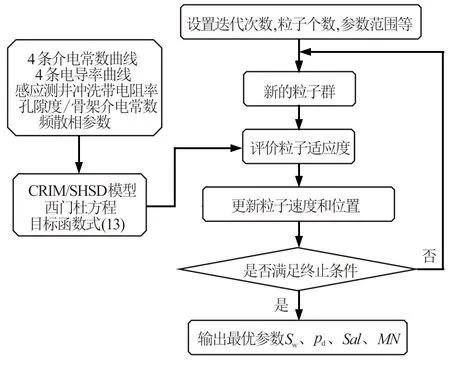
图1 联合电阻率测井和介电测井反演储层参数的流程

3 方法验证与实例计算

3.1 理想模型反演方法验证

根据已知假设理论模型的地层参数,基于式(1)～式(5)、式(10)和式(12),可计算得到介电测井在各频率下(22、100、350、960 MHz)的相对介电常数、电导率和冲洗带电阻率。本文假设2组理想模型实例进行计算,使用的地层参数见表1,实例A和B的相对介电常数和电导率的计算结果如图2所示,电阻率的计算值分别为34.41 Ω·m和13.25 Ω·m。图2中2组计算结果均显示:随着频率的增加,岩石相对介电常数减小,电导率增大。

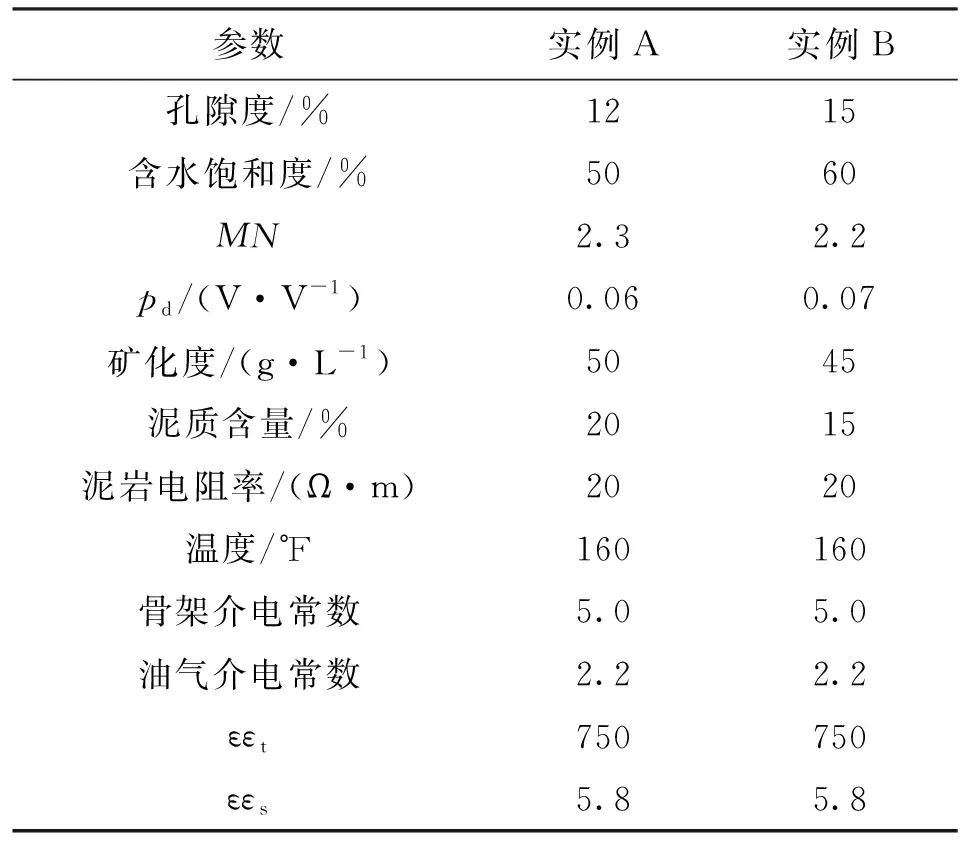
表1 假设的2组实例的岩石物理参数

图2 利用泥质砂岩和CRIM模型合成的介电常数和电导率响应值

将计算得到的上述2组理论值作为理想的测井值,将地层参数中的含水饱和度、水相曲折度指数、矿化度和泥质频散项体积含量这4个参数作为待求参数进行反演,其他岩石物理参数仍为已知量。图3展示了采用粒子群算法对参数进行寻优时的最优适应度曲线的变化,其中适应度曲线下降迅速,说明收敛速度快,当进化迭代次数超过50次后,适应度趋于稳定并逐渐达到最佳值,说明搜寻全局最优解能力强。最后,实例A的Sw、pd、Sal和MN的反演结果分别为50.00%、0.059 9、49.994 g/L和2.3,实例B的Sw、pd、Sal和MN的反演结果分别为59.90%、0.069 9、44.999 g/L和2.2,这与实际输入参数(见表1)吻合,表现出较好的反演效果。

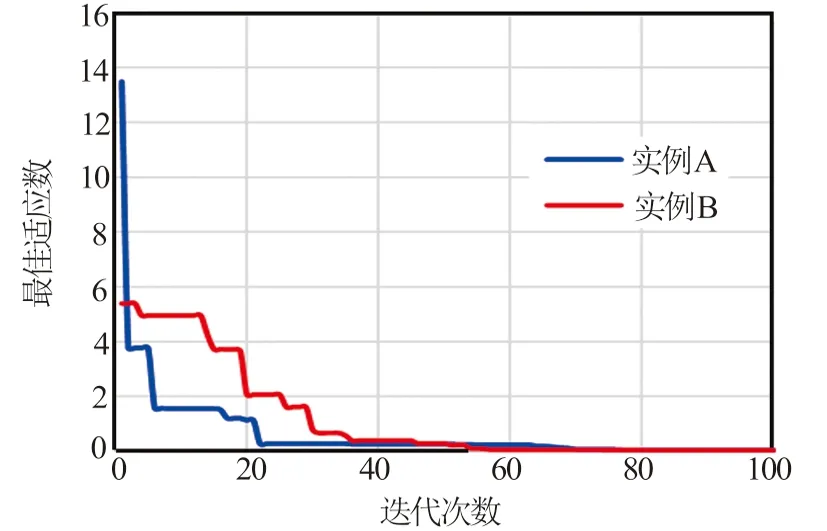
图3 2组实例迭代过程中的适应度曲线

3.2 实例计算

本次研究选取鄂尔多斯盆地L1井和L2井作为实例,收集了常规测井曲线、介电频散测井曲线以及岩心分析数据作为样本数据。常规测井数据用于计算储层的孔隙度和泥质含量,介电频散测井曲线包括在22、100、350 MHz和960 MHz频率下测量的介电常数和电导率,岩心分析数据包括孔隙度、含水饱和度和含油饱和度。

对L1井延长组长8段和L2井延长组长71段进行处理反演,计算致密砂岩储层含油饱和度。将反演得到的最优参数根据式(5)、式(10)和式(12)计算理论介电常数、理论电导率和理论电阻率的曲线响应值,并与实际测井曲线响应进行误差分析。电阻率测井曲线的相对误差Eres定义为

Eres=abs(lgRxo,meas-lgRxo,sys)/abs(lgRxo,meas)

(16)

式中,Rxo,meas为实际测量的电阻率,Ω·m;Rxo,sys为计算的理论电阻率,Ω·m。介电测井每种频率的参数值其平均相对误差Edielec利用Zhao等[8]定义的公式

abs(σmeas-σsys)/σmeas]

(17)

式中,εmeas为实际测量的介电常数;εsys为计算的理论介电常数;σmeas为实际测量的电导率,S/m;σsys为计算的理论电导率,S/m。

图4给出了某层段理论测井曲线和实际测井曲线的对比实例,其中第3道至第10道显示理论和现场测量的介电常数和电导率测井响应的对比。图4中,EPSI_XO_F0、EPSI_XO_F1、EPSI_XO_F2和EPSI_XO_F3分别代表介电测井仪器在22、100、350 MHz和960 MHz频率测量的相对介电常数;EPSI0、EPSI1、EPSI2和EPSI3是合成的对应频率的理论介电常数;COND_XO_F0、COND_XO_F1、COND_XO_F2和COND_XO_F3分别代表仪器在22、100、350 MHz和960 MHz频率测量的电导率;COND0、COND1、COND2和COND3是合成的相应电导率测井响应值。第11道为阵列感应测井电阻率曲线AT10(表示探测深度10 in)和合成的理论电阻率曲线Rxos。第12道和第13道中的ERR_F0、ERR_F1、ERR_F2和ERR_F3分别是在4种频率下正演合成的测井值和实际测井值的平均相对误差,ERR_RXO表示计算的和实际测量的冲洗带电阻率的相对误差。从第3到第11道可见,合成的测井曲线和实际测量的曲线吻合良好,二者数值接近,变化趋势也相同。在第12道和第13道中,定量计算的相对误差仅在X X55～X X56 m处较大,可能的原因是该深度段泥质含量较高,孔隙度较小(见图5)。其他深度段相对误差均较小,大部分数值小于10%,少部分高于10%但基本小于20%。这验证了该文提出的致密砂岩介电测井和电阻率测井曲线处理方法的准确性和可靠性。

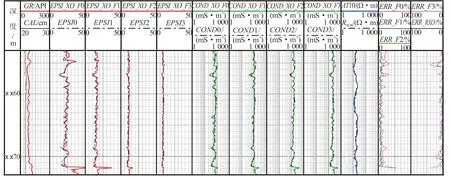
图4 L1井合成介电常数、电导率及电阻率测井曲线对比

图5 L1井延长组长8段水层常规测井、介电测井曲线及反演结果

图5显示了L1井的常规测井曲线、介电测井曲线和计算的储层参数,该井与图4为同一口井。图5中第3道显示了阵列感应电阻率曲线,其中AT10是探测深度最浅的电阻率。第5道和第6道为电导率和相对介电常数。常规经验公式计算的泥质含量和孔隙度见第7道,计算的孔隙度(φt)和岩心分析的孔隙度(φc)如第8道所示,二者吻合较好。第9道展示了反演计算的含水饱和度(Sxo),以及岩心分析含水饱和度(SWC)和含油饱和度(SOC)。第10道包含反演计算参数pd、MN和Sal,第11道和第12道表示反演方法计算结果的平均相对误差。

该层位为延长组长8段储层,试油结果为水层,岩心分析含油饱和度也表明该层含油性较差。从图5第9道可见,计算的整个层段冲洗带含水饱和度大多为1,只有2个小层有一定的含油性显示。第10道计算的MN基本上等于2,频散项体积含量pd值介于0.06～0.09,与计算的泥质含量有一定的相关性;冲洗带矿化度分布介于15～40 g/L,该值并不代表真实的地层水矿化度,而是介于地层水矿化度和钻井液矿化度之间。

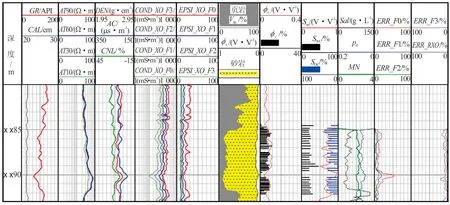
图6 L2井延长组长71段油层常规测井、介电测井及反演结果

图6展示了L2井延长组长71段储层常规测井曲线、介电测井曲线及其计算的反演参数,图6中所有曲线道与图5中一致。图6第11道和第12道显示该层段计算结果的相对误差基本小于10%,说明计算结果比较准确。该层段试油测试为油层,第10道岩心分析的含油饱和度也表明其含油性较好。反演计算结果显示:冲洗带含水饱和度除X X89.5～X X90.5 m外,介于60%～70%,显示较好的含油性;计算的冲洗带矿化度与L1井水层的矿化度计算值相近,pd和计算的泥质含量存在正相关性;MN值介于2.0～2.4,略大于L1井水层的MN值,说明油层中水的导电路径比水层的导电路径复杂。综上可知,本文提出的方法在实际应用中效果良好,验证了该方法的有效性和可靠性。