低渗透油藏直井压裂后产能高精度预测方法研究
2022-06-06许淑梅付晨东汪爱云宋延杰李雪英姜艳娇
许淑梅,付晨东,汪爱云,宋延杰,李雪英,姜艳娇
(1.中国石油集团测井有限公司大庆分公司,黑龙江大庆163412;2.东北石油大学地球科学学院,黑龙江大庆163318;3.东北石油大学非常规油气成藏与开发省部共建国家重点实验室培育基地,黑龙江大庆163318)
0 引 言
某油田LX地区X油层为低渗透油藏,砂泥岩薄互层广泛发育,储层物性差、油水关系复杂,导致测井压裂后(简称压后)产能预测结果与实际试油结果差异较大。由于压裂裂缝参数难以获取,致使不同的压后产能预测方法预测结果各不相同,导致压后产能预测精度较低。因此,有必要探索一种适用于低渗透油藏直井压后产能预测的方法。
近年来,专家学者在压裂后储层产能评价和预测方面开展了大量的研究工作,并取得了丰富的成果。储层压裂产能预测方法主要分为3种:①依据岩心、测井、测试等资料,选取可表征储层储集能力的参数和可表征压裂裂缝特征的参数,利用统计回归方法建立压后产能预测模型或产能级别预测模型[1-5];②根据油藏水力压裂施工工艺,基于裂缝形态、导流能力与油井产能关系,应用渗流理论建立压后产能预测模型[6-12];③采用油藏数值模拟方法,建立地层压裂仿真物理模型,结合压裂设计和历史生产资料进行压裂产能数值模拟研究,实现压裂产能动态预测[13-16]。统计回归方法着重探讨压后产能与各主控因素之间规律性控制关系;渗流公式法多从油藏渗流理论出发,探讨不同流型、流态的流体在油藏生产条件下的渗流规律,具有坚实的物理基础;而油藏数值模拟方法,可以克服压裂裂缝形态复杂及参数不易获取的技术难题,利用已知油藏特征参数,采用正演模拟技术研究不同裂缝形态、不同裂缝参数情况下的垂直井产能变化情况,为压裂设计、施工提供技术指导。该文结合3种方法的各自优点,提出针对低渗透油藏压后产能预测方法,为研究区压后产能预测研究提供理论及技术指导依据。
1 压后产能主控因素分析
压后产能与储层物性、品质、流体性质、压裂施工参数和生产动态参数密切相关,如何从众多参数中优选出主控因素,进而获得压后产能与主控因素之间内在的规律性控制关系,是实现压后产能有效预测的必然途径。
1.1 产能参数的优选
日产油量、米平均日产油量和产油指数作为描述产能的参数,哪个参数具有全区可对比性,需要优选确定。利用试油数据将单层产油量与生产压差进行相关性分析,发现单层日产油量不随生产压差变化。因此,在多元统计回归建模中可以排除生产压差因素,即产油指数与米平均产油量是等价的。分别将试油日产油量和压后米平均日产量与渗透率绘制交会图,发现随着渗透率的增大,日产油量增加,但二者相关性很差;而压后米平均日产油量与渗透率内在控制性关系非常好,相关系数为0.82[见图1(a)],这证明采用压后米平均日产油量比单层日产油量的预测精度高。因此,最终选定米平均日产油量作为产能预测的统计变量,在后续的建模中使用。
1.2 地层电阻率与压后产油量的关系
对于低渗透油层,电阻率的大小体现储层束缚水饱和度的高低;对于油水同层,电阻率则体现可动水饱和度的高低。因此,在考察产油量与电阻率关系时,应充分考虑纯油层与油水同层这2种情况,即在产油量预测中包含产水率Fw的影响。依据X油层10口井68个层试油数据建立压后米平均产油量与地层电阻率交会图[见图1(b)]。由图1(b)可知,X油层电阻率与压后米平均产油量相关性较好,随着储层电阻率的增加,压后米平均产油量增大,相关系数为0.58。
1.3 加砂量与压后产油量的关系
加砂量是体现压裂裂缝最终形态的参数,其在一定程度上决定了压后产能的大小。而研究区压裂资料中的加砂量均为合层加砂量,为了与单层产油量匹配,本文将加砂量细分到小层,即细分小层加砂量=合层加砂量×细分小层有效厚度/合层厚度。其中,合层加砂量为试油及压裂报告中的多层合试加砂量;细分小层有效厚度为扣除夹层后细分小层厚度;合层厚度为未扣除夹层的多层合试储层厚度。
为准确反映加砂量对储层渗流的改善情况,筛选出压前、压后均有试油的储层。首先,考察压后日产油量与加砂量之间的统计关系,发现单层压后日产油量与加砂量相关性很差,相关系数只有0.13,说明加砂量与压后产油量之间不存在控制关系。转而计算6口井15个层的压前、压后米平均产油量的差量,再与加砂量开展统计分析,建立米平均产油量的差量与加砂量的交会图[见图1(c)],发现米平均产油量的差量与加砂量相关性好,随着加砂量的增加,米平均产油量的差量明显增大,相关系数为0.83。该方法不仅验证了理论分析的正确性,而且确立了加砂量与压前、压后产能的内在关系,为压后产能预测模型的建立奠定了基础。
1.4 压后产油量与其他参数之间的关系
建立压后米平均产油量与孔隙度之间的交会图[见图1(d)],发现产油量与孔隙度关系密切,相关系数达0.89,说明压后产油量受孔隙度的控制。分别考察米平均产油量与标准化密度、自然伽马、声波时差、补偿中子的统计关系,发现压后米平均产油量与标准化的密度、自然伽马具有很好规律性,相关系数分别达0.56、0.78[见图1(e)、(f)],而与声波时差、补偿中子关系不大。因此,压后产油量高低受标准化密度和自然伽马控制。分别考察层产油量与原油黏度、原油密度的关系,发现层产油量与原油密度、原油黏度存在一定关系,但规律性不强。同时原油黏度和原油密度是以小层为测量单位的,无法匹配到米平均,因此,在该研究中把二者作为压后产能的次要因素,在多元统计回归模型中忽略其影响。
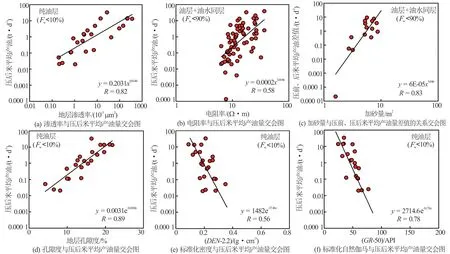
图1 压后米平均产油量(或与压前米平均产油量的差值)与各参数之间统计关系
米平均产油量可以消除不同井之间层厚的影响,是一种标准化参数,具有区域可比性。从上述研究发现米平均产油量与渗透率、孔隙度、电阻率、加砂量、标准化密度、标准化自然伽马具有很好的规律性,说明压后产能与储层岩性、物性、含油性密切相关。因此,优选上述参数与米平均产油量建立多元统计回归压后产能预测模型。
2 多元统计回归法预测压后产能
2.1 模型的建立
根据上述压后产能主控因素研究,可知压后日产油量与储层物性参数、测井响应参数和压裂施工参数具有乘幂或指数关系,反映出压后日产油量与各参数之间的内在控制关系。以上述单因素幂次或指数关系为控制变量,采用多元优化方法确定各个参数的最优权系数,建立多元统计回归模型。由于参与建模的参数个数、组合关系不同,导致模型最后预测精度不同。因此,以压后试油资料为基准,对多种参数组合进行多元统计回归模型优选。计算每种模型日产油量预测的相对误差,以相对误差最小为最优模型选取准则,最终选定孔隙度、渗透率、深电阻率、伽马、密度、加砂量等6个参数和压前米平均日产油量qoi建立X油层压后米平均日产油量的多元统计回归预测模型。
为了使预测模型更好地适用于低渗透储层,按照产能的不同级别采取分段回归方式,以提高模型预测精度。通过模型优选,最后确定X油层的压后米平均日产量分段预测模型,见式(1)~式(3)所示。
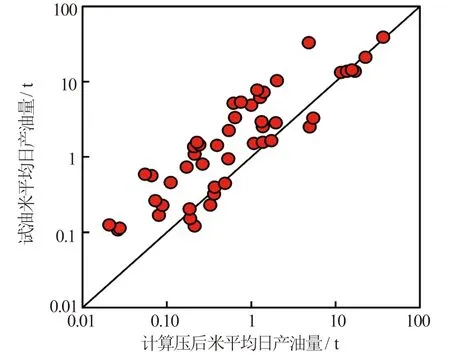
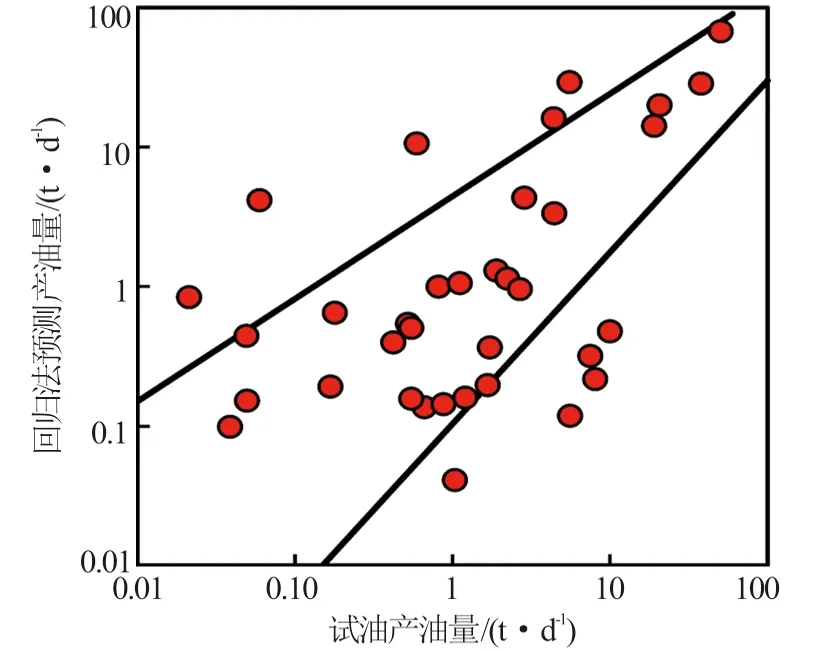
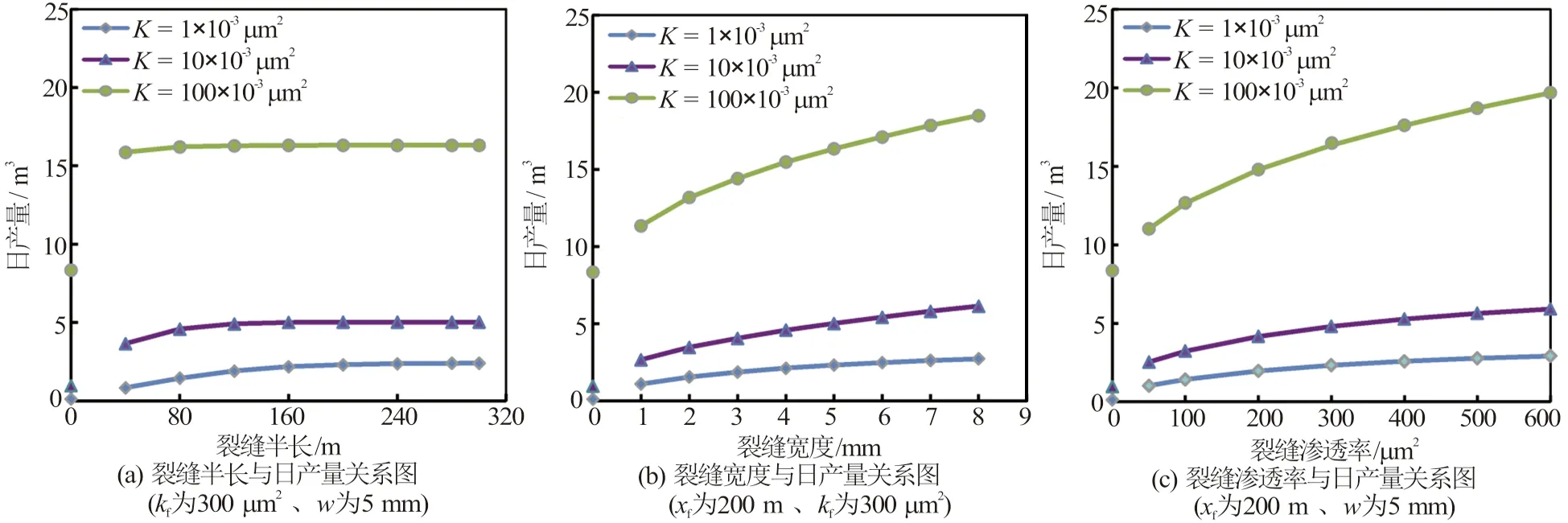
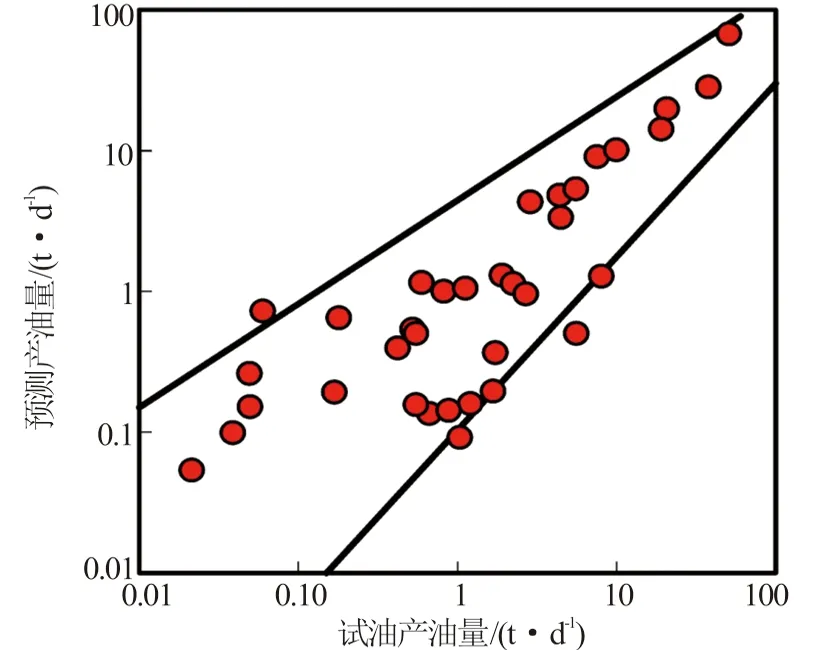
当0.1 (1) 当1 (2) 当qo>10时, (3) 式中,qo为压后米平均日产油量,t·d-1;φ为孔隙度,%;K为渗透率,10-3μm2;Rt为储层电阻率值,Ω·m;GR为储层标准化自然伽马值,API;DEN为储层标准化补偿密度值,g·cm-3;SD为储层加砂量,m3;qoi为压前米平均日产油量,t·d-1。 其中,压前米平均日产油量采用压前产能预测回归公式法求取,见式(4)~式(6)所示。 当0.04 (4) 当0.1 (5) 当qoi>1时, (6) 式中,CN为储层标准化中子测井值,%;AC为储层标准化声波时差值,μs·ft-1(1)非法定计量单位,1 ft=12 in=0.304 8 m。 利用上述预测模型计算的压后米平均日产油量与建模所使用的试油产油量之间的平均相对误差为48.4%(见图2),表明多元统计回归产能预测模型具有较高的精度。 图2 回归法计算压后产油量与试油产油量对比图 选取研究区16口试油井和压裂井共35个小层,应用多元统计回归压后产能预测模型进行压后产油量预测,以压裂后试产油量为对比基准,选取每小层产能预测相对误差作为符合率计算的控制标准发现:产能基数越大,控制相对误差越小,控制精度要求越高,即当产能基数为100 t·d-1时,控制相对误差设为30%,预测产能在70~130 t·d-1,可判定符合;当产能基数为1 t·d-1时,控制相对误差设为100%,即预测产能在0.1~2.0 t·d-1,可判定符合(见图3中的两条黑线之间),从而定量计算产能预测符合率。将计算结果与试油结果进行对比分析(见图3),与试油产油级别符合的共25层,产油级别符合率为71.4%。表明该文所建立的多元统计回归方法能够基本满足储层压后产油量的精度要求。 图3 回归法预测产油量与试油产油量对比分析图 综合上述实际井处理与应用效果分析可知:多元统计回归法多使用储层参数、测井响应参数及工程参数,参数相对较少且容易确定,无传递误差,适用性强。但是该方法区域经验性强,一些动态参数(压差、流体黏度)和裂缝参数(裂缝宽度、裂缝长度、裂缝渗透率)都无法在模型中体现,导致个别井少数层产能预测误差较大,必须采取新的方法对误差较大的预测点加以矫正。 对于多元统计回归法预测误差较大的层位,考虑是压差、黏度等生产动态参数和裂缝相对导流能力在油气产出中起到决定性作用,而多元统计回归法无法体现上述因素,造成预测精度的不足。因此,对于这些层位,应基于渗流理论,充分考虑上述因素的影响,建立渗流方程并加以改进。 Raymond和Binder[7]基于三角形裂缝形态,利用等值渗流阻力法,通过求解二区(考虑近井地层污染情况)复合介质稳态渗流数学模型,建立了地层损害条件下垂直裂缝井近似压后产能计算公式。根据Raymond-Binder数学模型 (7) 式中,p为压力,kPa;r为地层半径,m。 利用X油层已知的边界条件,求式(7)的特解 (8) 式中,pe为油层压力,kPa;pwf为井底压力,kPa;re为供油半径,m;rw为井筒半径,m。 利用Darcy定律,可得到X油层产量公式 (9) 式中,q为压后日产油量,t·d-1;h为被压裂储层的有效厚度,m;B为原油体积系数;μ为原油黏度,mPa·s。 对于近井地层存在污染的情况下,渗透率分布存在下述规律 (10) 利用各个区间积分结果,得到压后产能预测公式 (11) 式中,xf为压裂裂缝半长,m;Kf为裂缝渗透率,10-3μm2;w为裂缝宽度,m;rs为污染带半径,m;Ks为污染带渗透率,10-3μm2。 根据研究区地层条件、储层岩石物理特征和流体性质,基于两相流流体渗流理论,利用油藏数值模拟方法,建立垂直井地层模型,在地层模型裂缝产生的位置采用网格细化方式并赋予相应的裂缝参数,模拟在地层压力与井底流压的压力差作用下,压裂井油水两相产能情况。分别设定地层渗透率为1、10和100×10-3μm2,研究高、中、低渗储层压后产能的变化规律。 (1)裂缝半长对压后产能的影响。图4(a)给出不同裂缝半长(40~300 m)单井压后日产油量的模拟结果。当地层渗透率为100×10-3μm2时,裂缝半长对产油量影响不大。对于低渗透油藏,随着裂缝半长的增加,单井日产油量增加,说明裂缝半长对压裂井有明显的增产作用。当裂缝半长增加至200 m时,单井日产量增加不显著,说明当裂缝增加到一定幅度时,油井产量趋于平稳。所以,200 m裂缝半长是低渗透油藏增产的最大裂缝长度。 图4 裂缝参数与日产量关系 (2)裂缝宽度对压后产能的影响。图4(b)给出不同裂缝宽度(1~8 mm)单井压后日产油量的模拟结果。随着裂缝宽度的增加,单井压后日产油量呈增加趋势。对于渗透率为1×10-3μm2的低渗透油层,当裂缝宽度增加到5 mm时,继续增加裂缝宽度产油量增加不显著。 (3)裂缝渗透率对压后产能的影响。原油的日产油量与裂缝渗透率密切相关。图4(c)给出不同裂缝渗透率(40~600 μm2)对压后日产油量影响。数值模拟计算结果表明,随着裂缝渗透率的增加,单井日产油量明显增加。 在实际应用中,一般设定污染带半径为0.8 m,污染带渗透率为地层渗透率的十分之一;由于裂缝渗透率和裂缝宽度无法精确确定,根据油藏数值模拟结果,设定裂缝渗透率为300 μm2、裂缝宽度为5 mm;裂缝半长可以根据压裂液体积与裂缝半长之间的线性关系进行定量估算。 针对多元统计回归方法预测结果与试油结果不符的层,应用三角裂缝压后产能预测公式进行压后产油量预测,以压裂后试产油量为对比标准,将公式法、回归法结合预测的结果与试油结果对比分析(见图5)。与试油产油级别符合的共31层,产油级别符合率为88.6%,说明多元统计回归方法与渗流公式法相结合可以大幅提高压后产能预测符合率。 图5 公式法与回归法结合预测产油量与试油产油量对比分析图 (1)X油层压后产油量的主要影响因素为渗透率、孔隙度、电阻率、自然伽马、密度及加砂量,在此基础上,建立了基于储层物性参数、测井响应参数、工程参数的储层压后产能统计回归预测模型。通过实际16口井的35个小层产能解释验证,产油量符合率为71.4%。 (2)在无法得到压裂裂缝参数信息情况下,采用油藏数值模拟方法,确定出低渗透储层最大裂缝长度为200 m、最宽裂缝宽度为5 mm,这为渗流公式法提供有力的参数选取依据。 (3)多元统计回归法使用储层参数、测井响应参数和工程参数,参数相对较少并容易确定,应用效果好,但存在区域经验性强、动态参数、裂缝参数无法体现的问题,导致部分层位出现较大预测误差;而渗流公式法理论性强,考虑了压差、流体黏度、裂缝相对导流能力等动态参数的影响。两种方法结合可以较大地提高产能预测精度,改进后的产油量模型预测符合率达88.6%,证明两种方法相结合在研究区压后能有效进行产能预测。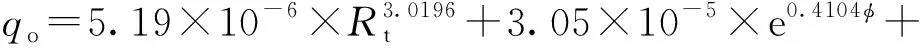
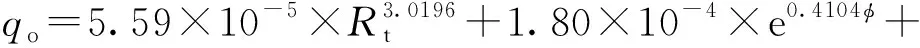
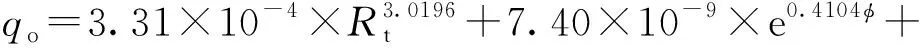
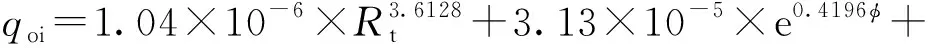
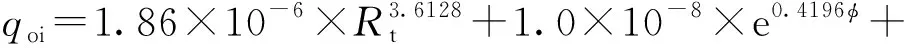
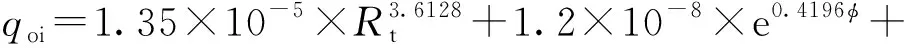
2.2 应用效果检验分析
3 渗流公式法预测压后产能
3.1 渗流公式法
3.2 油藏数值模拟方法确定裂缝参数
3.3 基于公式法的压后产能计算
4 结 论
