针对滑坡位移监测的数据预处理方法研究

2022-06-06王勇董欣悦刘先林刘定祥

西部交通科技 2022年3期

关键词：卡尔曼滤波滑坡

王勇　董欣悦　刘先林　刘定祥

摘要：文章以滑坡变形监测中最常见的位移实时监测数据为例，采用卡尔曼滤波、拉依达准则、最小二乘法等方式对监测数据进行预处理，实现异常值的识别与数据的波动平滑，以减少数据的异常波动干扰，更准确反映滑坡变形过程，为预警系统提供更科学有效的数据。

关键词：滑坡;拉依达准则;卡尔曼滤波;数据预处理

中图分类号：U416.1+63

0 引言

滑坡是常见的地质灾害，在我国山区，每年都有滑坡灾害发生，造成巨大的生命财产损失。为减少滑坡灾害影响，实现提前感知与防范，可对滑坡进行实时自动化变形监测。但在实际监测过程中，有许多客观环境和人为因素导致测量数据有各类误差因而使得预测结果出现偏差。因此，为了保证滑坡灾害预测的准确性，应该先对监测数据进行预处理，从而达到更为理想的数据曲线，提高预警的准确率。本文针对滑坡自动化监测中的位移数据，采用拉依达准则来判断数据采集过程中所出现的粗大误差，进行异常数据剔除，再利用卡尔曼滤波对数据进行去噪，使得数据的噪声减小，从而降低拟合时的误差，最终将数据用最小二乘法进行拟合，得到更为准确、平滑的数据曲线，能够直观地为预警系统提供更科学的数据，提高预警的准确率。

1 异常数据识别

1.1 基于拉依达准则的识别方法

在对滑坡进行实时监测时获取的数据往往会因为各种客观和人为因素导致异常值，例如设备本身会产生一定的误差，也可能因环境、气温的变化产生误差。而在数据采集时，若监测体系被破坏、人为操作误差或者碰动仪器也会引起监测序列中产生较大异常值。对于数据样本中的异常偏离点，在预处理中往往会采取剔除处理。常用的异常数据判别法则有拉依达准则、肖维勒准则、格拉布斯准则、狄克逊准则、t检验和极差法等。拉伊达准则，又称3σ准则，其适用于样本数量n≥10并且可以计算样本数据{X}（i=1，2，…，n）的算术平均值X—和标准差的情况。针对服从正态分布的测量时间序列，对{X}以30为控制限构建控制限区间（μ-3σ ，μ+3σ）进行异常值识别。本次试验所采用的数据体量足够大且数据总体服从正态分布，故采用无须查表的简便的拉依达准则。拉依达准则将在区间内的数据定义为正常数据，将不属于区间内的数据定义为变形数据。

由于此时的置信概率为99.73%，基本满足统计特性，因此可以有效地判别大偏移数据在监测序列中的异常值存在情况。

对于裂缝计所给定的测量次数充分大的样本数据，可以采取拉依达准则来判断残余误差，从而进行异常值剔除。

通过计算出样本标准差σ后，根据拉伊达准则确定一个控制限区间（μ-3σ，μ+3σ），对超出该区间的数据认为是粗大误差予以剔除。

1.2 异常位移数据识别

以滑坡监测中常见的裂缝计实时数据为例。该原始数据中存在某些数据因客观环境、人为因素等原因所造成的裂缝计位移，从而导致某些采集值异常偏大。这种在观测过程中所产生的不符合正态分布的粗大误差，会导致在对数据进行拟合时的均值产生整体偏移。而使用拉依达准则进行判别，可对数据中的异常值进行剔除。某滑坡隐患点的裂缝原始监测数据如图1所示。

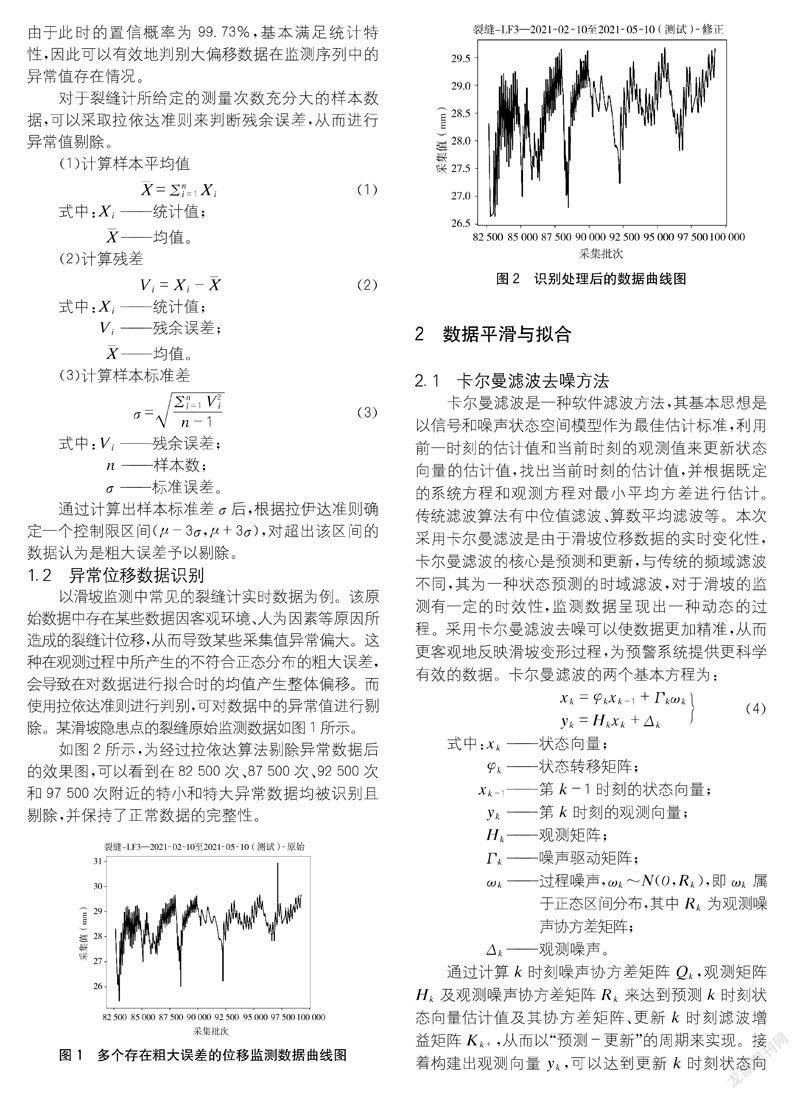
如图2所示，为经过拉依达算法剔除异常数据后的效果图，可以看到在82 500次、87 500次、92 500次和97 500次附近的特小和特大异常数据均被识别且剔除，并保持了正常数据的完整性。

2 数据平滑与拟合

2.1 卡尔曼滤波去噪方法

卡尔曼滤波是一种软件滤波方法，其基本思想是以信号和噪声状态空间模型作为最佳估计标准，利用前一时刻的估计值和当前时刻的观测值来更新状态向量的估计值，找出当前时刻的估计值，并根据既定的系统方程和观测方程对最小平均方差进行估计。

传统滤波算法有中位值滤波、算数平均滤波等。本次采用卡尔曼滤波是由于滑坡位移數据的实时变化性，卡尔曼滤波的核心是预测和更新，与传统的频域滤波不同，其为一种状态预测的时域滤波，对于滑坡的监测有一定的时效性，监测数据呈现出一种动态的过程。采用卡尔曼滤波去噪可以使数据更加精准，从而更客观地反映滑坡变形过程，为预警系统提供更科学有效的数据。卡尔曼滤波的两个基本方程为：

通过计算k时刻噪声协方差矩阵Qk，观测矩阵Hk及观测噪声协方差矩阵Rk来达到预测k时刻状态向量估计值及其协方差矩阵、更新k时刻滤波增益矩阵Kk+，从而以“预测-更新”的周期来实现。接着构建出观测向量yk，可以达到更新k时刻状态向量估计值及其协方差矩阵的目的。

式中：Rk[DW]——第k时刻观测噪声协方差矩阵。

卡尔曼滤波的估计值要通过反向滤波进行最优的固定区间平滑处理，需要计算出k时刻反向滤波增益矩阵Kk-和反向滤波状态向量估计值及其协方差矩阵。

式中：

K——用于加权平均的平滑增益矩阵;

x+和P+——正向滤波估计中的xk和Pk;

x-和P-——反向滤波估计中的xk+1和Pk+1;

xs和Ps——平滑后的待估参数估计值及其协方差矩阵。

2.2 去噪方法应用

算法中通过在实例变量中存储各种矩阵来实现过滤器，所有卡尔曼滤波器都以“预测-更新”周期运行。使用方法或函数 “predict（）” 实现的 predict 步骤使用状态转换矩阵F来预测下一个时间段（epoch）的状态。状态存储为高斯（x，P），其中x是状态（列）向量，P是其协方差。协方差矩阵Q指定过程协方差。使用方法或函数“update（）”实现的更新步骤将具有协方差的测量值z合并到状态估计值（x，P）中。

图3所示为裂缝数据通过卡尔曼滤波去噪算法后的效果，能明显看出数据噪声减小，滤波后曲线更加平滑。

2.3 最小二乘拟合方法

最小二乘法通过最小化真实值和预测值的误差（残差）的平方和来寻找数据的最佳函数匹配，利用最小二乘法可以较好地进行数据拟合。

对于在时间x得到的观测值y，假设存在以下的函数关系：

式中：c1，c2，…，cm——m个需要通过实验来确定的参数。

对于n>m，设测量过程中的系统误差可忽略或已修正，则在xi时的观测值yi围绕着期望值f（xi;c1，c2，…，cm）波动，其分布可认为符合正态分布，则yi的概率密度为：

式中：σ——正态分布标准误差。

对于n组观测数据（xi，yi），i=1，2，3，…，n，若n≤m，则将数据代入式（14），无法确定所有参数。

考虑到各次测量相互独立，则yi的似然函数为：

2.4 数据拟合实现

由于在滤波去噪后的数据仍然较为跳动，故而在卡尔曼滤波去噪的基礎下对算法进行了改进，添加了最小二乘法的曲线拟合，选取拟合曲线时按照偏差平方和最小的原则，并且采用二项式方程为拟合曲线。

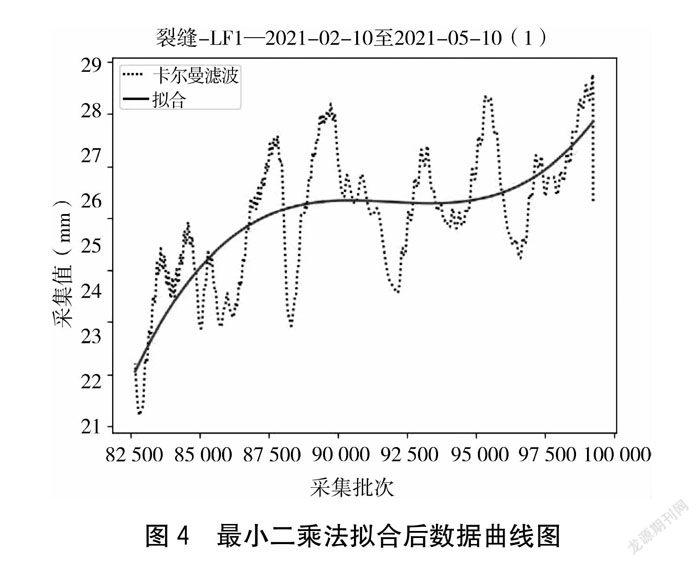
图4所示为使用了最小二乘法拟合后的数据曲线图。由图4可见拟合后的曲线相比于使用单一卡尔曼滤波去噪后的曲线更加平滑。