基于SIMULINK 的水轮机调速器建模与仿真研究

张海明，刘 珺，梁一笑，梁 云

（1.广西水利电力职业技术学院，广西 南宁 530021；2.南宁市食品药品安全信息与监测中心，广西 南宁 530000）

0 引言

在水轮机控制系统的设计或改进过程中，既需要进行理论分析计算，通常还需要进行性能实验研究。但是，在现有的水轮机控制系统上进行实验很可能会对系统的正常运行造成影响，而且费用高、时间长、危险性大，系统控制参数的设置和操作条件都不够理想，所以很多时候对模型的实验研究就尤为必要。由于水轮机调节系统的物理模型比较复杂，建立起来需要耗费大量的人力、财力和物力，时间又长，重复利用率还不高。基于此，更多地通过建立数学模型来对水电机组控制系统进行仿真，可以对它的静态和动态特性进行经济、方便、直观、迅速的研究。由于水轮机控制系统是一个非线性的、非最小相位的复杂系统，加之在建立数学模型的过程中，难免要对次要的因素和模型进行简化处理，要想通过仿真准确地反映水轮机控制系统的实际过程并得到定量的结论是十分困难的。因此，只能从定性的、比较的意义上对其进行仿真，为现实的水轮机控制系统的设计和改进提供有参考价值的数据[1-5]。

1 MATLAB 软件及SIMULINK 仿真模块

MATLAB 软件是当今世界上最优秀的数值计算软件之一，可以用来方便地进行矩阵运算及控制和信息处理。MATLAB 计算功能强大，图形功能丰富，适用范围广；编程效率高，扩充能力强，兼容性好；语句简单，易学易用；自动控制软件工具包功能齐备，这些优点使得MATLAB 成为目前控制领域内被广泛采用的计算机辅助设计和控制系统计算、仿真软件[6]。

SIMULINK 是MATLAB 软件的图形化仿真工具，可以用来对动态系统集中进行建模、仿真和分析，不仅支持连续、离散及两者混合的线性和非线性系统仿真，还可以进行多速率系统仿真。SIMULINK 仿真环境具有开放性、可视化的特点，与传统的仿真软件包相比，更直观、方便和灵活。此外，SIMULINK 还提供了封装和模块化工具，实现对仿真模块库的扩展，特别适用于多层次、高非线性的复杂系统仿真。可以大大简化设计流程，降低设计成本、提高工作效率。

SIMULINK 仿真环境中包含有一系列模型库，用户也可以根据自己的需求定制和创建合适的模块。SIMULINK 还为用户提供了用方框图进行建模的图形接口，采用这种结构建模就像利用笔和纸来画一样容易。在定义完成一个模型以后，用户可以进行仿真和分析其动态特性。在仿真进行的同时，还可以采用Scope 模块和其他的显示模快直观地看到仿真的结果。除此之外，用户还可以实时观察在改变系统参数后系统中发生的变化。仿真的结果还能以变量的形式保存并输入到MATLAB 的工作空间里做进一步的优化分析、处理或利用。

2 水轮机调节系统的数学建模

水轮机调节系统通常由引水系统、水轮机、发电机及负荷、机械液压系统和调速器等组成，是一个包含水力、机械、电气的复杂的控制系统。在对实际环境模拟中，还加入了水头、水流扰动模块[7]。图1 为水轮机调节系统的各模块原理图。

图1 水轮机调节系统原理框图

水轮机调节系统的难点集中在水轮机和引水系统上面，其在调速过程中具有非线性、实时变化等特点，常规的反馈控制难以实现。为了便于仿真，接下来对系统中的各个组成部分分别建立传递函数模型。

（1）水轮机调速器的PID 调节模块：

式中：KP为比例增益，整定范围为0.5 ～20；KI为积分增益，整定范围为0.05 ～10（1/s）；KD为微分增益，整定范围为0 ～5 s。

（2）机械液压随动系统可以用一阶惯性环节表示，其传递函数为：

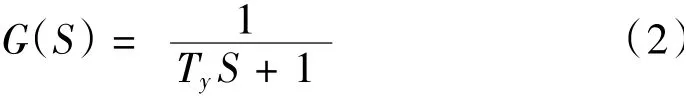
式中：Ty为接力器响应时间常数，一般取0.05 ～0.2 s。

（3）水轮机及引水系统用下面的公式表示：

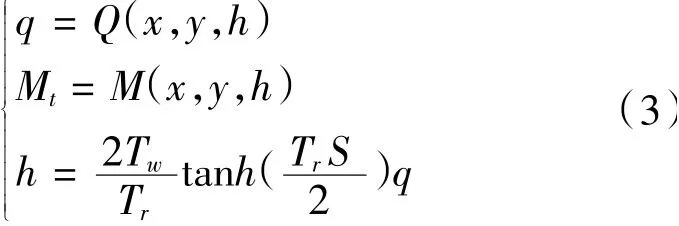
由公式可知引水系统具有非线性的最小相位特点，可以近似用弹性水击模型来表示：

式中：h为水头大小；q为水流流量；Tw为引水系统的水流惯性时间常数，一般Tw= 0.5 ～4 s；Tr为管道反射的时间常数。

对水轮机的某个工况点以局部线性化的方法可以表示如下：

x为转速；y为接力器行程；h为水头；ex、ey、eh、eqx、eqy、eqh为水轮机的传递系数。

其传递函数为：

对于理想水轮机，有：eqx= 0、eqh= 0.5、eqy= 1、eh=1.5 并且取ey= 1，则传递函数可以简化为：

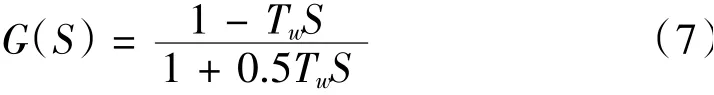
（4）发电机及负荷模块也用一阶惯性环节来简化表示，其传递函数为：

式中：Ta为机组惯性的时间常数，一般Ta= 3 ～12 s；en为机组静态频率的自调节系数，一般en= 1。

根据水轮发电机组的线性化数学模型可以看出，水轮机的调速系统是一个高阶系统。水轮机及其引水系统的特点又使该系统具有非线性和时变特性。对于线性化模型G（s）来说，这些特性集中体现在模型的参数随着工况的变化而实时改变。

3 水轮机调节系统的SIMULINK 仿真

在采用SIMULINK 进行仿真时，只需要将各对应于图1 的模块取出，把传递函数式1、2、7、8 代入相6应的模块，然后用鼠标将它们联起来，就可以构成图2 所示模型，再设置合适的仿真参数，即可对水轮机调节系统进行仿真。

由图2 可看出，在SIMULINK 环境下进行仿真时所建立的仿真系统充分采用了模块化设计的概念，其开放性和可移植性都很强，且易于修改模型结构，适合水电站个性强的特点。

在图2 中，当选择开关S1 不接负荷扰动的时候，系统仿真的是空载扰动工况，仿真波形如图3～图10（纵轴为频率，横轴为时间）：

图2 水轮机调节系统SIMULINK 仿真框图

图3、图4 是当机组处于空载状态时，分别对机组进行1Hz 上扰和下扰所生成的仿真频率曲线。在空载扰动的仿真过程中，当我们代入多组PID 参数时，部分有代表性的仿真曲线如图5 至图10 所示。从中选出相对较优的一组，保证机组在空载时能稳定运行，并作为后续实验研究的初始参数。

图4 空载扰动仿真曲线2（1Hz 下扰）

比较图3、图5 和图6 可以看出，KP越大，系统的响应速度越快，但将产生超调，当KP值取过大（KP＞10），系统开始振荡、不稳定；如果KP值取较小时响应速度缓慢，调节时间延长，使系统动、静态特性变差。

图5 空载扰动仿真曲线3（1Hz 上扰）

图6 空载扰动仿真曲线4（1Hz 上扰）

比较图3、图7 和图8 可以看出，引入积分环节作用系数KI的目的是消除系统的稳态误差。KI越大则积分速度越快，系统静差消除也越快，同时KI越大引起响应过程出现的超调也越大，导致其动态性能变差，当KI值取的过大（KI＞2），系统开始振荡、不稳定；若KI过小，则积分作用不明显，使系统的静差消除困难，导致过渡时间加长，从而影响系统的调节精度以及动态特性。

图7 空载扰动仿真曲线5

比较图3、图9 和图10 可以看出，微分环节作用系数KD越大，超调相应越小，调节系统则越稳定。但KD过大，就会导致响应过程提前制动，从而拉长调节时间，系统的抗干扰性也较差，当KD取值过大（KD＞8），系统开始振荡、不稳定。

图3 空载扰动仿真曲线1（1Hz 上扰）

图10 空载扰动仿真曲线8（1Hz 上扰）

当选择开关S1接负荷扰动的时候，系统仿真的是并网负荷扰动工况，仿真波形如图11 和图12 所示。

图12 机组甩100%负荷频率曲线

图11、12 所示分别是机组在甩25%和100%负荷时的仿真的频率曲线。从空载扰动和并网甩负荷的仿真结果可以看出：所设计的水轮机调速系统在机组各种波动过程中都表现出较好的调节性能，很好地满足了电站各项运行的需求，实现了预定的设计目的。

图11 机组甩25%负荷频率曲线）

4 系统实验研究

实验研究对象为采用PWM 控制方法，基于PLC的高速开关阀控制的调速器，该调速器的结构如图13 所示。

相应的性能参数如下：

额定油压：31.5MPa 蓄能器容积：10L

油泵输油量：8L/min 电机功率：3kW

接力器容积：0.4L 接力器行程：70mm

按图13 连接好相应的元件和管路。参考前面仿真结果，把其中较为理想的仿真参数作为实验的初始设置参数。依据相关标准进行实验，结果见表1。

图13 试验调速器结构示意图

表1 频率与脉冲信号记录表

4.1 静特性试验

对调速器系统做静特性实验，绘制静特性曲线如图14 所示，测得转速死区为0.008%，非线性度0.3%，永态转差系数最大值10%。

图14 调速器静特性曲线

4.2 随动系统扰动试验

图15为频率模式下，接力器处于稳定状态，频率给定为50 Hz，给随动系统输入0.4 Hz 机频扰动时PID 的输出y随时间的变化情况。图16 为这一过程中，接力器的相对开度Xy的随动过程，它反映了高速开关阀控制的电液随动系统的动态品质。从图中可看出Xy刚开始时上升得非常快，之后出现较小的超调达到稳定状态，接着有一小段保持恒定，这反映了随动系统的死区，走出死区后跟随PID 输出同步上升至目标值。

图15 PID 输出特性曲线

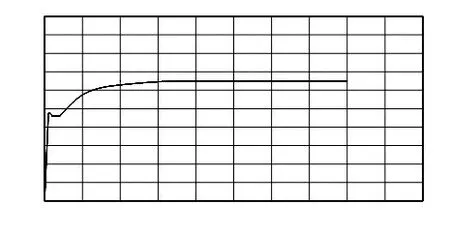
图16 接力器导叶开度曲线

5 结论

本研究建立水轮机调速控制系统的数学模型，在Matlab SimuLink 环境下进行了仿真，从空载扰动和并网甩负荷仿真曲线可以看出所设计的调速系统在机组大、小波动过程中均表现出优良的调节性能。对比不同的仿真曲线，可以明显看出不同的PID 参数对系统控制性能的影响。对设计的水轮机调速器在实验室进行了空载状态下的静特性试验，随动系统扰动试验，证明了其在空载工况下具有较好的控制性能。