基于Q-learning的弹道优化研究

周毅昕，程可涛，柳立敏，何贤军，黄振贵

(1.南京理工大学 钱学森学院，南京 210094;2.南京理工大学 瞬态物理国家重点实验室，南京 210094)

1 引言

传统的弹道优化程序计算量大、计算时间过长、同时还要求较高的计算资源，倘若每一次都需要实弹打靶势必会耗费很多的人力、物力，且拉长研发周期。因此更加精准、更加便捷、更加快速的弹道优化过程亟待开发研究。

机器学习目前被广泛运用于各个领域，如聂凯等根据深度强化学习的高效性提出了人工智能的军事应用前景，李先通等用强化学习的方法建立了一种时空特征深度学习模型，实现了对下一时隙的路径行程时间进行预测，选择最优路径；赵绍东提出基于机器学习的支持向量机机器学习的(SVM算法)模型进行建筑耗材降价分析与研究，得出建筑耗材价格选择的优化方案。张蕾等围绕机器学习技术提出了面对海量数据效率更高的安全问题解决方案。最新更为高效精确的气体传感器，保证全局收敛和计算高效的梯度算法，都离不开机器学习的思想与帮助。机器学习会不断扩充它的教学数据，使程序在学习的过程中逐渐变得更加“智能”，且机器学习的主要作用是预测，从而得到最优决策。

本文将机器学习中具有高效率、低损耗、高精确特点的强化学习与弹道优化问题相结合，提出了基于强化学习的弹道优化研究，以期将二者结合，改进现有弹道优化方法中存在的不足，推动我国弹道优化研究朝着智能化方向发展。

强化学习在弹道优化中的作用与传统函数相比，其优点在于不需要建立弹道优化的数学模型，即传统弹道优化过程中所需要的优化目标函数、约束函数、选取优化设计变量与关联方程都不需要在机器学习中建立，取而代之的是弹载计算机在不断的迭代学习过程中，调整导弹在飞行过程中不同状态下的指令控制，来达到最优目标的控制效果。

本文将弹道方程组与Q-learning算法相结合，研究基于Q-learning算法的机器学习在弹道优化上的应用，给出在Q-learning算法下弹道优化结果，并与参考模型的计算结果进行对比，以验证机器学习与弹道优化相结合的可行性。

2 弹道模型建立与求解

2.1 无控弹道方程组

为了构建标准条件下的质点弹道基本方程，计算中采取了以下假设：

1) 在导弹飞行的任何阶段，导弹攻角均为0;

2) 不考虑风速等其他因素的影响，导弹仅受重力和阻力影响;

3) 假设地面为无限扩展的水平面，不考虑地球表面曲率影响;

4) 忽略科氏惯性力;

5) 导弹结构视为一个质点，仅在3个方向上的平动，不存在转动。

结合以上假设，从最简单的弹道方程组模型入手，建立了炮弹在3DOF(自由度)的只受重力和阻力的外弹道方程组作为参考模型，模型具体如下所示：

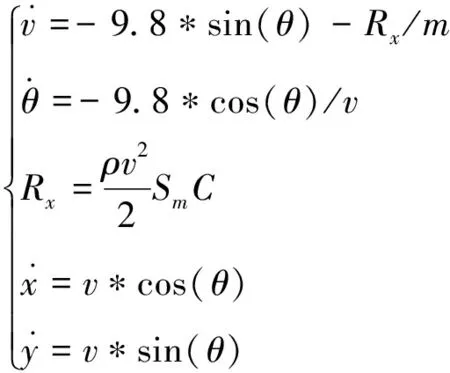
(1)

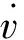
2.2 弹道优化方法

传统的弹道优化方法主要有利用高斯伪谱法将弹道最优控制问题转化为非线性规划问题，进而用SQP算法求解弹道优化设计问题；或者利用hp自适应伪谱法进行离线弹道优化，得到多条最优弹道控制数据后训练BP神经网络，得到神经网络制导控制器；或对导弹优化计划建立相应模型，采用分段优化全程弹道的方法。

四阶龙格库塔法的截断误差、时间复杂度和空间复杂度都很好，常使用于工程上求解常微分方程的问题。因此本文选择龙格库塔法对弹道方程组求解。

3 强化学习及Q-learning算法

3.1 强化学习

强化学习是机器学习中的一个分支领域，在强化学习中，智能体通过不断“试错”的方式进行学习，在智能体与环境的不断交互下，获得奖赏，并在价值策略的驱动下朝着最大化累计奖励的方向迭代优化，从而不断提高智能体自身的决策能力。首先环境会给智能体一个观测值(状态)，智能体在接收到环境给的观测值之后，在价值策略的引导下进行决策并做出动作，与智能体进行交互的环境在动作的作用下发生变化，即从状态A转移到状态B，并向智能体返回状态B以及相应的奖励值。智能体会根据环境给予的奖励更新自己的策略，从而实现在探索环境的同时，更新自己的动作策略，进而优化自身的决策能力。本文选取强化学习中较为基础典型的Q-learning算法进行研究。

3.2 Q-learning算法介绍

Q-learning算法是强化学习算法中价值本位(value-based)的算法。Q代表s和a的价值函数Q(s,a)，即在某一时刻的状态(state)下，采取某一动作(action)能够得到的奖赏的期望。Q-learning算法的思想核心就是将某一时刻的状态和动作以及其能够得到的奖赏期望构建成为一张Q表来储存Q值。Q值如表1所示，a表示智能体可选择的动作，s表示智能体所处的状态，奖赏值为在该状态做出该动作时，环境所反馈的回报(reward)的估计值。例如，Q(s1,a1)= -1代表智能体在s1状态下做出a1动作，可获得的奖赏值为-1。

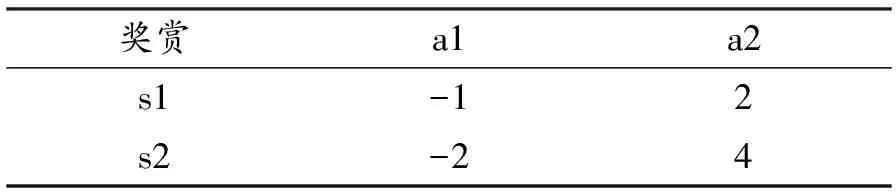
表1 Q值

3.3 Q表更新方法

Q表的更新以时间差分法的方式进行，其具体公式如下：

(,)←(,)+[+max′(′,′)-(,)]

(2)

其中:为奖励性衰变系数(衰减因子)，为控制收敛的学习率。当0<<1时，通过不断地尝试搜索空间，值会逐步地趋近最佳值。决定时间的远近对回报的影响程度，表示牺牲当前收益，换取长远收益的程度。

在下一个状态′中选取最大的(′,′)值乘以奖励性衰变系数再加上真实回报值作为的现实值，而把过往Q表里的(,)作为的估计值。以表1为例，具体实现步骤如下：

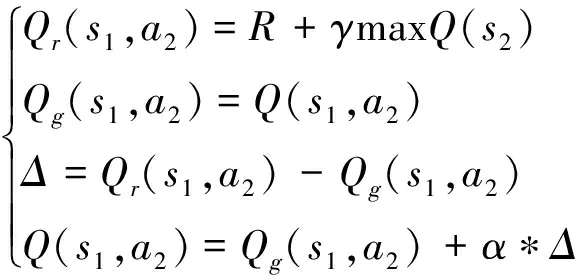
(3)

式中：为的现实值；为的估计值；为现实值与估计值的差值。

具体实现代码如下:

1) 构建并初始化Q表；

2) 初始化导弹运动状态参数 ;

3) 根据导弹状态基于策略选择动作;

4) 根据动作更新状态信息与反馈奖励;

5) 根据新的动作得到的反馈更新Q表；

6) 进入下一个状态，判断是否完成训练轮次；

7) 重复步骤2～6直到回合结束；

()的估计不仅仅只有这个状态，按照同样的规则持续展开，可以发现，其与后续、，…都有关系，这些都能够用来估计实际值，当衰减因子按以下3种情况取值，分别为：

()=+()=+*[+()]=

+*[+[+()]]()=

+*+*+*+*+…

(4)

为1 时，相当于完全考虑未来的奖励，没有忽略，即：

()=+1*+1*+1*+1*+…

(5)

在(0～1)范围内时，数值越大，对未来情况的重视程度越大，可以说智能体越有远见,即:

()=+*+*+*+*+…

(6)

当为0时，完全不考虑将来的情况，只有当前的回报值，即：

()=

(7)

3.4 基于Q-learning算法的简控弹道方程组

在对炮弹进行控制优化时，强化学习算法将弹载计算机作为智能体，将飞行过程中的炮弹的姿态、运动等外界信息视为环境，并以炮弹的飞行速度方向与水平方向间的夹角(弹道倾角)作为状态，智能体(弹载计算机)的动作为给炮弹施加垂直于速度方向的加速度，以此不断改变炮弹的飞行轨迹。

因此，基于Q-learning算法的简控弹道方程组可在参考弹道方程组的基础上得到，具体如下：

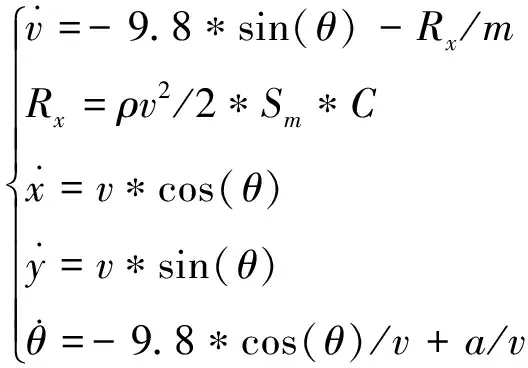
(8)

其中：为智能体作用的加速度；其余变量与式(1)中相同。

4 仿真校验

假定空气密度为1.206 kg/m，炮弹最大横截面积为0.018 86 m，阻力系数为0.25；炮弹质量为30 kg，直径为155 mm，出膛速度是800 m/s。

当出射角为45°时，基于Matlab采用四阶龙格库塔法对参考模型进行求解，可得到炮弹无控飞行轨迹如图1，射程是14 532.84 m，后文将通过与优化后射程进行对比验证Q-learning算法在弹道优化上的可行性：

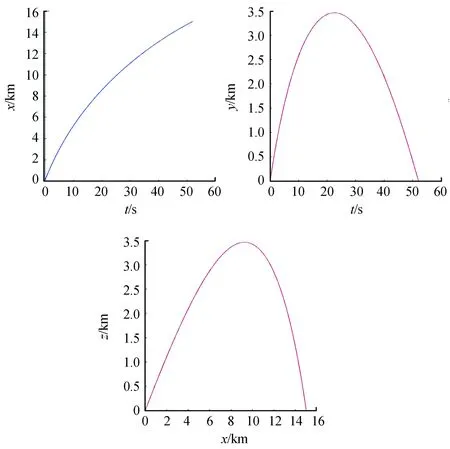
图1 炮弹无控飞行轨迹曲线

以最远距离为目标进行优化时，在30°、35°、40°、45°、50°、55°、60°初始弹道倾角进行3DOF弹道控制，其他初始参数与无控状态一致，测量无控情况下和在Q-learning模型中给法向过载进行控制的距离进行仿真，其中Q-learning算法的学习效率为0.05，贪婪度为0.8，奖励折扣为0.99，状态选择为速度与水平面间的夹角，动作为作用于垂直速度方向向上或向下，大小为5 m/s的加速度，优化结果如表2所示。

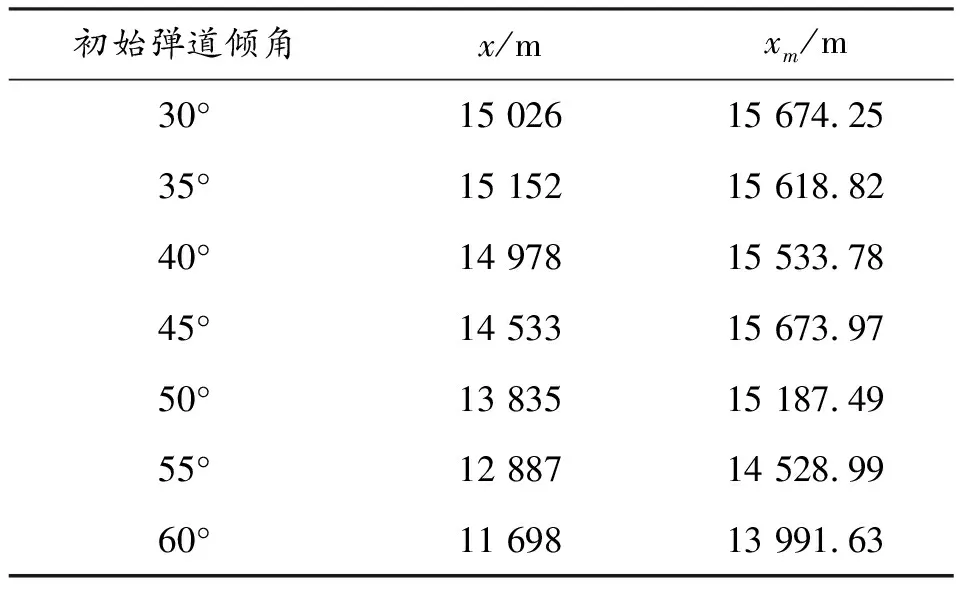
表2 以最远距离为目标的优化与无控弹道的结果

为炮弹在无控情况下落点处的距离；为Q-learning算法中有控(存在法向过载)情况下的落点距离。由表可知，针对不同的初始弹道倾角，Q-learning算法均能不同程度的提升炮弹的射程，可知Q-learning强化学习算法在以最远距离作为优化目标时具有较好的优化作用。

在有阻力情况下，当初始倾角为30°时以最远飞行距离为目标时，进行了1 000次Q-learning强化学习训练后的机器控制结果如图2所示。

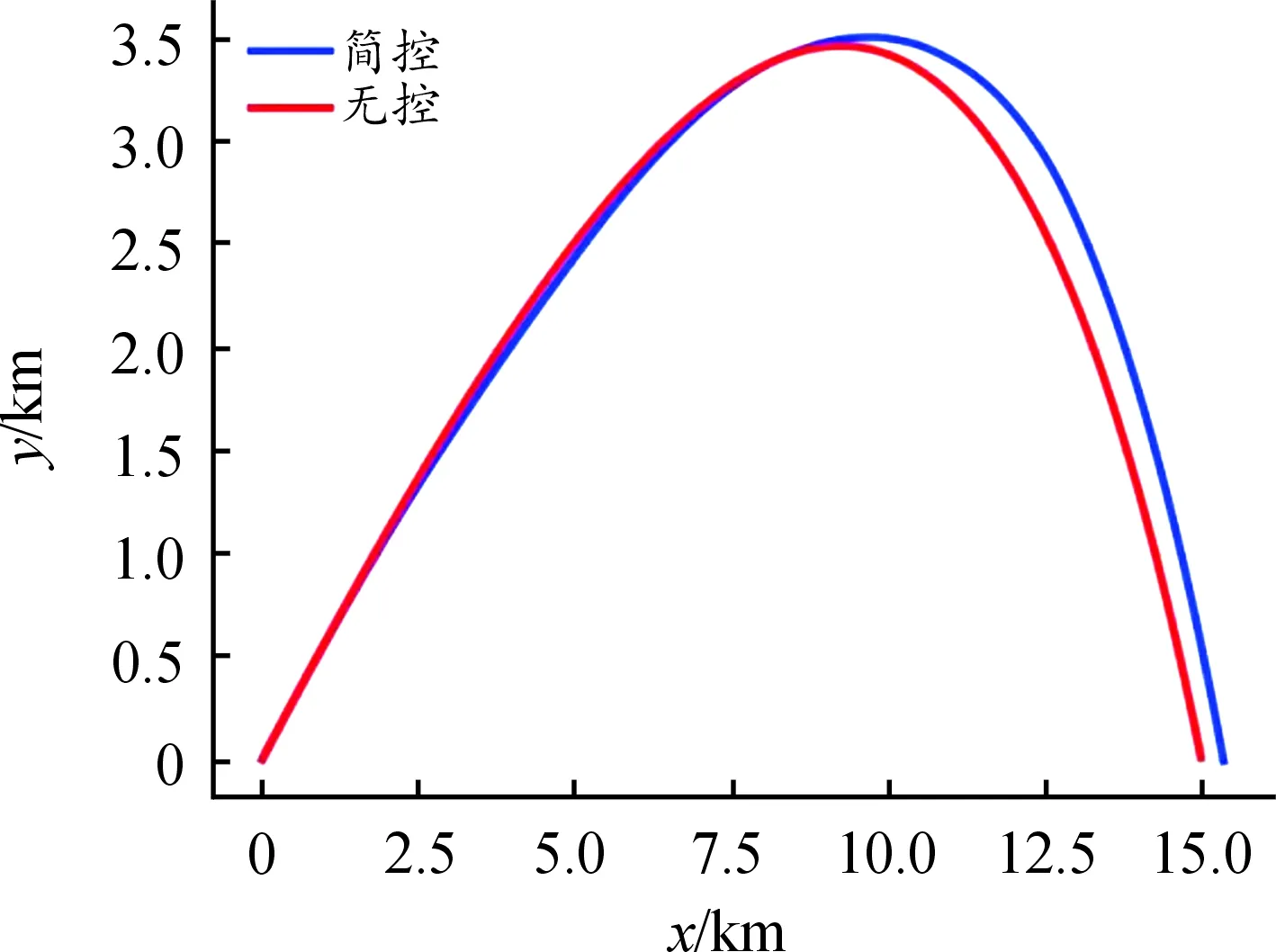
图2 最远距离控制结果曲线

图2中，横坐标为炮弹的水平飞行距离，纵坐标为导弹的飞行高度。炮弹从膛内以一定的初速度斜向射出去，可以看作水平方向上受外界阻力的直线运动和竖直方向上受重力的上抛运动的合成运动。由图2可知，与无控情况下进行对比，经过Q-learning强化学习训练后的最远飞行距离为15 674.25 m，大于无控状态下的最远飞行距离15 026 m，增加了4.3%。

图3表示了该次飞行过程中智能体进行1 000次强化学习过程中对炮弹做出的控制动作过程。图中以加速度的离散数据_mean作为纵坐标，以时间为横坐标。加速度为智能体每一次采取动作直接产生控制后炮弹的过载，加速度的波动曲线是在+5和0的离散动作区间内智能体所采取的动作集合。通过实时产生加速度指令，实现控制弹体姿态，进而控制弹道轨迹。

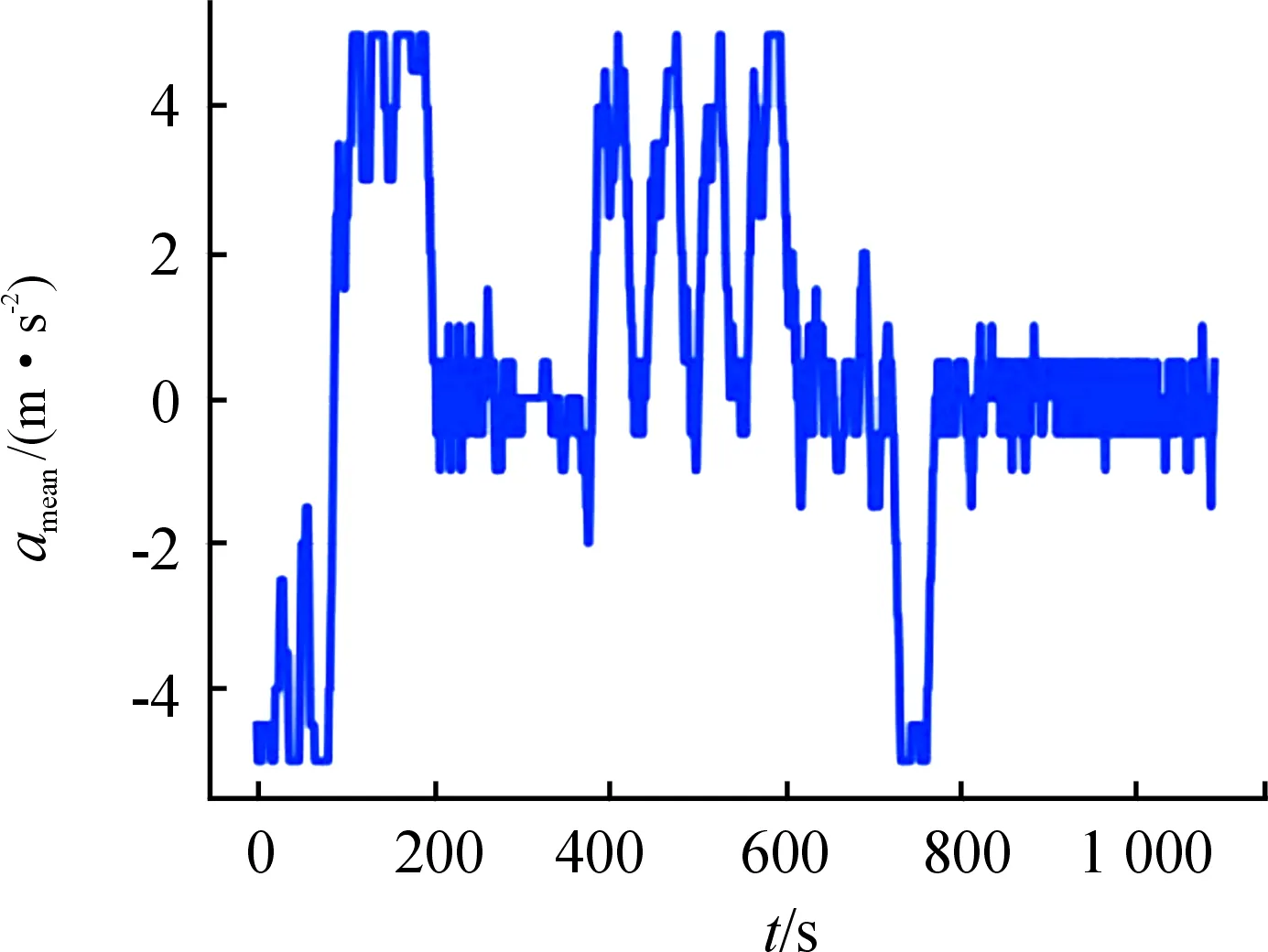
图3 飞行过程中的控制结果曲线

以最大落点速度为目标进行优化时，同样在30°、35°、40°、45°、50°、55°、60°初始弹道倾角进行3DOF弹道优化控制，仿真计算无控情况下和在Q-learning算法中控制法向过载的最大落点速度，优化结果如表3所示。

表3 以最大落点速度为目标的优化与无控弹道的结果

如表3所示，表示炮弹在无控情况下落点处的速度；表示在Q-learning模型中给法向过载的情况下的落点处的速度。由表3可以看出，优化后的炮弹落点速度均大于无控条件下的炮弹速度。

当初始倾角为30°时，以最大落点速度为目标，进行1 000次Q-learning强化学习后控制结果如图4所示。

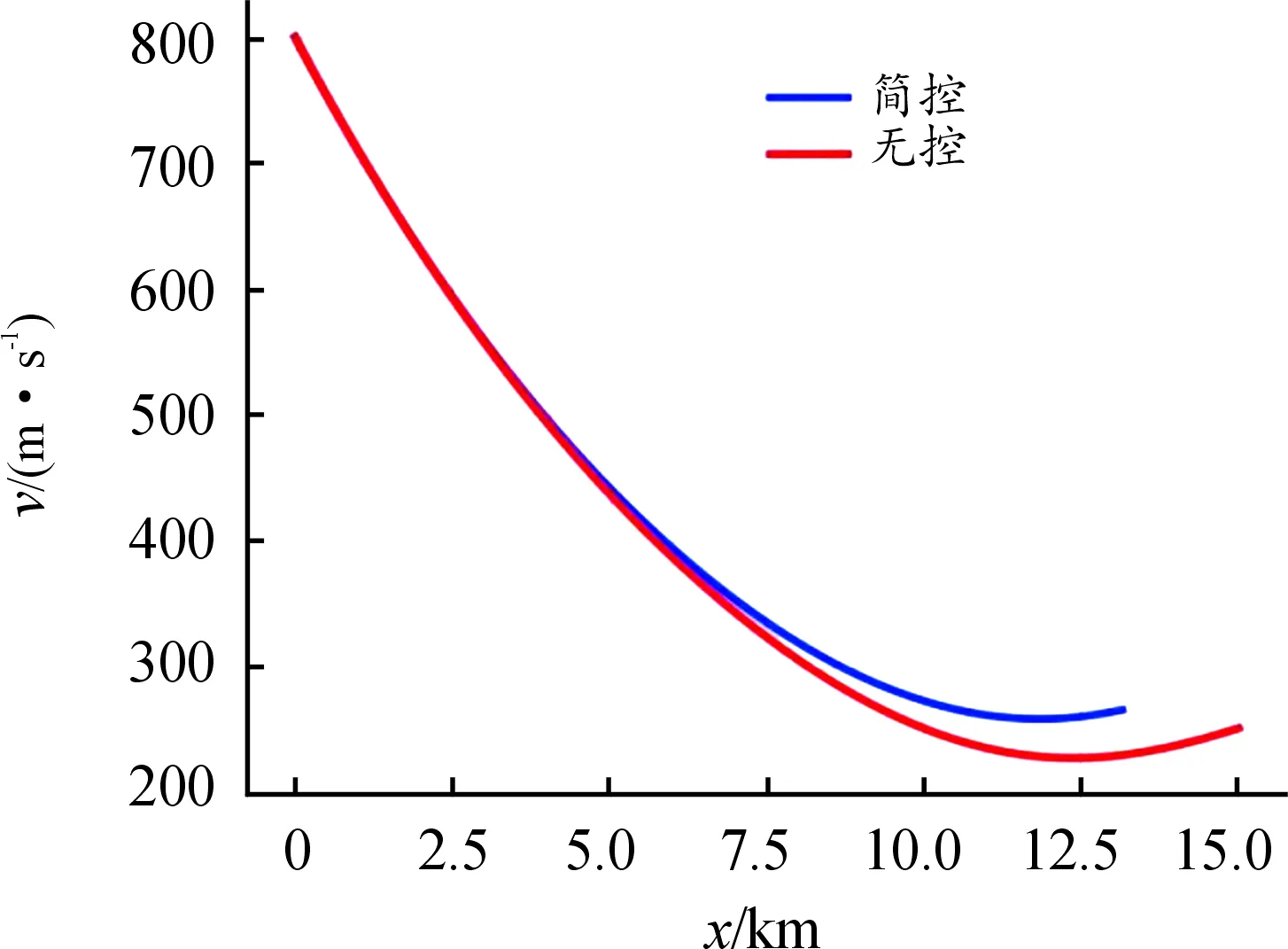
图4 最大落点速度控制结果曲线

其中横坐标为炮弹飞行的水平距离，纵坐标为炮弹的落点速度，由图4可以看出在炮弹抵达最高点前，由于空气阻力的存在炮弹的速度有减小的趋势，在开始下落后炮弹速度开始增大，图4曲线可以看出在速度降到最低(即飞行过程达到最高点)后有上扬的趋势。通过分析比较发现，经过优化学习后的最终落点速度大于无控状态下的落点速度。

初始倾角为30°的优化过程如图5所示，以加速度的离散数据_mean作为纵坐标，以控制时间作为横坐标，其加速度曲线波动原理与图3一致。

图5 飞行过程中的控制结果曲线

5 结论

提出了一种基于强化学习中Q-learning算法的制导炮弹简控弹道优化控制方法，该方法效率高，能有效提升射程，具有通用性。以最远射程和最大落点速度为目标时，智能体经过学习后对弹道的优化控制能满足预期要求，能够通过Q-learning算法进行弹道优化。初步证实了机器学习在弹道优化上的可行性，为后期进一步探索打下基础。

对于不同的优化目标，该优化方法只需改变Q-learning算法中的环境约束条件，就能得到对应的弹道优化控制结果。