油纸绝缘介电响应宽频等效建模研究

顾朝亮，朱孟兆，朱文兵，张家瑞，李红娥

（1.国网山东省电力公司电力科学研究院，山东 济南 250003；2.山东电力研究院，山东 济南 250003；3.国网山东省电力公司东营供电公司，山东 东营 257000；4.国网山东省电力公司夏津县供电公司，山东 德州 253200）

0 引言

电气设备的运行状态对电网整体的运行可靠性具有十分关键的影响。在电网中，大多数高压电气设备采用了油纸复合绝缘作为其主绝缘结构，例如变压器套管、互感器等。这类设备常年运行于较为复杂的负载条件下，其绝缘可靠性面临着严峻的威胁［1］。其中，内绝缘问题是高压电气设备绝缘故障的主要类型，例如，高压设备内部油浸纸绝缘系统中的水分会导致3 方面的问题：降低介电强度、增加气泡的排放、加速纤维素老化［2］。由此可见，为保证电气设备的实时运行安全，准确跟踪及监测高压设备的绝缘状态（如绝缘受潮、老化等）至关重要，有助于及时发现绝缘问题，并提前采取相应措施以排除潜在故障。

目前，国内外学者提出了多种绝缘状态诊断方法。其中，基于电介质介电弛豫理论的介电响应测试方法—回复电压（Recovery Voltage Method，RVM）、极化/去极化电流（Polarization/Depolarization Current，PDC）以及频域介电谱（Frequency Domain Spectroscopy，FDS）是应用较为广泛的3 种油纸绝缘非侵入式诊断测量方法［3-4］。而FDS 测量因其在现场操作中的低噪声敏感性，低测试电压（通常峰值小于200 V），以及宽泛的测量频率范围而具有显著的优势［5］，FDS技术可对电网中关键油纸绝缘设备进行科学有效的状态监测和诊断。

在此背景下，从理论方面，需要研究如何对FDS的测试结果进行有效解释，以更好地理解和分析FDS 数据所携带的绝缘状态信息，用于支撑FDS 的现场诊断应用。目前，关于介电响应解谱方法主要可分为以下几类：将介电响应与标准化样本（也称为“指纹”）的介电响应进行比较，以对绝缘状态进行定性判断［6］；对油纸绝缘系统进行等效建模，以匹配响应曲线，进而得出模型参数与绝缘状态之间的变化关系［7］；从介电响应曲线推导出某些数值特征，并与表征绝缘状态的直接参量指标（例如水分百分比或聚合度（Degree of Polymerization，DP））进行拟合，以得出两者之间的定量公式［8］。在这3 种途径中，介电响应等效建模的思路更加符合油纸绝缘这一真实的物理系统，并能直接联系起介电行为的宏观响应和微观过程，且通过比较有限数量的模型参数值比研究响应曲线更直观准确。从上述模型的观点出发，对油纸绝缘宽频介电响应问题展开了模型化研究，采用扩展德拜等效电路模型，将改进的人工蜂群算法同序列二次规划算法进行结合，实现在宽频测量范围内（0.001～5 000 Hz）对FDS 曲线的精确建模，为下一步研究模型参数与绝缘状态的定量关联关系，进而提取绝缘诊断特征量奠定前期基础。

1 介电响应理论基础

1.1 弛豫极化

当电介质在未充电的情况下，材料中无积蓄的单极性电荷。此时，每种绝缘材料在原子水平上都由在微观和更宏观尺度上相互平衡的负电荷和正电荷组成。当材料暴露于外施电场（或由嵌入绝缘体中的电极间电压所产生的内电场）时，正负电荷就会定向移动，从而形成不同种类的偶极子。当等量正负电荷q的“重心”分开一小段距离d时，在中性物质（原子或分子）内将“诱发”局部电荷的不平衡现象，从而产生了偶极子的偶极矩：p=qd，这与作用在物种附近的“局部”或“微观”电场E 有关，该过程称为电介质的极化过程。当外施电场为交变电场时，偶极子将跟随该电场发生周期性的偏转，且当电场频率足够高时，偶极子转向将无法跟上电场方向的改变而出现滞后现象，此即弛豫极化［9］。笔者主要关注电介质的弛豫极化，因其受材料状态的影响很大，只要对绝缘材料中的弛豫极化信息进行充分解读，即有望实现根据弛豫极化信息反推油纸绝缘状态。因此，拟对油纸绝缘介电响应中的弛豫极化过程进行等效建模，为油纸绝缘状态的定量诊断提供模型基础。

1.2 扩展德拜模型

根据弛豫极化的滞后表现特点，介电响应可以用扩展德拜模型（Extended Debye Model，EDM）［10］进行等效，如图1 所示。该模型通过引入了多条阻容串联支路的并联结构，对不同弛豫时间的偶极子群进行等效表征。图中，R0为几何电阻，R（qq=1，…，Q）为极化电阻，C0为几何电容，C（qq=1，…，Q）为极化电容。

在图1的电路结构对照下，FDS频域介电响应的3个核心谱参量（复电容实部、复电容虚部、介质损耗角正切）可写为：

图1 扩展德拜模型

式中：C′（ω）为复电容的实部部分；C″（ω）为复电容的虚部部分；tanδ为介质损耗角正切；ω为角频率。

本质上，该模型将实体油纸绝缘系统视为“黑匣子”，而本文的目标是确定出一组Rq和Cq，从而使最终介电响应方程式（1）—式（3）符合实验测量的FDS数据。同时，获得的Rq和Cq的取值大小还应符合一定的物理意义。

2 实验样品的制备及其FDS测量

2.1 样品制备

油纸电容式套管是一种典型的油纸绝缘设备，其主要实现设备引出线与设备外壳之间的电气绝缘及机械固定作用［11］，其内绝缘主体由绝缘纸裹制的电容芯体和绝缘油填充而成。从套管对于油纸绝缘结构的代表性及套管绝缘状态监测的实际意义出发，选择油纸电容式套管作为介电响应等效建模研究的具体对象。通过对不同内绝缘状态的套管进行FDS 实测，可提供用作建模分析的真实FDS 数据源。考虑到实验操作的可行性及实验条件的定量控制问题，采用一种缩比尺寸的变压器套管模型开展介电响应实验，如图2 所示。该模型设计了真实套管最基本的内部和外部绝缘结构设计，但电容芯子中的铝箔层较少，因而体积较小，便于实验操作。

图2 实验用缩比套管模型

套管样本的制备流程如下：首先，对新的电容芯子和绝缘油进行真空干燥48 h，然后将经过真空干燥的电容芯子在60℃条件下浸入干燥的绝缘油中48 h，并充入氮气24 h，以确保电容芯子充分浸油。为了得到不同状态的油纸绝缘样本，以受潮为电容芯子的目标状态，将电容芯子置于空气中，并开启加湿器进行人工吸湿，以模拟不同程度的受潮情况，定期使用天平对芯子主体的增重进行称量，制备出了3组不同含水量的芯子，其水分含量相对于电容芯体的质量分数分别为0.71%、1.1%和2%。电容芯子制备完成后，将芯子、瓷套及附属金具进行组装，并最终充入绝缘油完成套管样本的整体制备过程，主要制备过程如图3所示。

图3 套管样本的主要制备过程

2.2 频域介电响应FDS测试

完成套管的制备后，对3 组套管样品进行了介电响应测试，测量仪器装置如图4 所示，仪器型号为DIRANA 介电响应分析仪。使用温度箱分别控制箱内温度为35℃、50℃、65℃、80℃，在此温度下，分别测试3 组套管在0.001～5 000 Hz 频率范围内的介电响应。

图4 套管介电响应测试装置

图5 绘制了套管介电响应的部分测试结果，tanδ反映的是绝缘的损耗大小信息，频段内总共有26个频点数据，每个测量频点对应3个谱参量值，用于下述扩展德拜模型参数计算。由于篇幅限制，仅给出了水分含量为0.71%下不同温度影响的tanδ曲线（图5（a））和在测试温度为35℃下不同水分质量分数影响的介质损耗正切tanδ曲线（图5（b））。如图5（a）所示，tanδ反映的是绝缘的损耗大小信息，随着温度的增加，曲线向右平移，曲线的最低点保持不变，满足Arrhenius 关系式［12］。图5（b）显示随着绝缘水分质量百分数的增加，曲线整体抬高，且低频段最为明显（＜1 Hz）。

图5 介电响应测试结果

3 建模及分析

3.1 目标及算法

本文的核心问题是如何根据上述实测的FDS 数据计算出扩展德拜模型中的各电阻、电容组件参数，以完成对油纸绝缘介电响应的参数化建模。该问题为非线性多参数最优化问题，首先建立最优化目标函数如式（4）所示。

式中：下标“测量”代表相关实测值；下标“拟合”代表根据某次参数辨识结果实时得出的对应参量计算值；w（ωm）为施加在第m个测量频点ωm的数据拟合误差项权重；M为总测试频点的个数。

采用一种改进的人工蜂群算法（Artificial Bee Colony，ABC）［13-14］同序列二次规划（Seqential Quadratic Programming，SQP）［15］的融合算法对上述最优化模型进行了求解。

人工蜂群算法虽然具有很强的全局搜索能力，避免了局部极小点。但是，算法缺乏局部搜索能力和准确性。因此，将ABC 和基于梯度的SQP 相融合。基于两种算法各自的优缺点，由ABC算法负责初始解，然后由SQP 进行二次优化。该融合算法利用ABC 在全局搜索中的优势先定位出一个初略解，为SQP 算法在附近进行进一步的精确搜索提供合理的初值，然后利用SQP 算法的局部快速准确收敛特性最终确定出一个精确解。作为一种十分成熟的传统算法，SQP的基本原理不再赘述。

ABC 是一种进化算法，该算法将最优化模型最优解的搜寻过程模拟为蜜蜂种群的蜜源寻觅行为。例如，搜索每个解的过程都包含了一个表示食物来源位置的参数集，而解的“健康值”指的是与食物位置相关联的食物来源质量。这个过程模拟了蜜蜂寻找有价值的蜜源过程，也即对应了一个寻找最优解的过程。一个蜂群的最小模型由3 类蜜蜂组成：被雇佣的蜜蜂、跟随蜂和侦察蜂。被雇佣的蜜蜂负责调查蜜源，并与引来的跟随蜂分享信息。反过来，他们会根据这些信息来决定是否选择该食蜜源。质量高的蜜源比质量低的蜜源更有可能被选中。对于每只被雇佣的蜜蜂而言，如果它的蜜源被雇佣蜂和跟随蜂拒绝，它就会变成一只侦察蜂。与其他群算法类似，ABC 算法是一个迭代过程，它从一群随机产生的解开始迭代，在满足终止条件之前，将重复以下操作：派出雇佣蜂、跟随蜂选择蜜源、确定侦察蜂，对应的具体算法步骤如下。

1）对于n=0 时刻，首先随机生成可行解，记为代表蜜源的数量。这些解与蜜源一一对应。除上述可行解外，其余可行解的生成式为

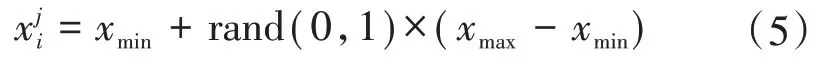
式中：j=（1，2，…，Np），但j≠i，表示在Np个蜜源中随机选取的不等于i的蜜源，将上述组合成初始解，即跟随蜂的初始位置下标min代表对应变量的给定最小值，下标max 代表对应变量的给定最大值，则xmin和xmax为整个解空间的上、下界；rand为函数名称，代表随机函数，则rand(0，1)表示取值在［0，1］之间的随机数。然后，计算初始可行解X0的适应度函数，根据适应度函数大小进行排序作为初始的采蜜蜂种群。

2）对于第n步的采蜜蜂位置采用式（6）进行更新。

3）当采蜜蜂更新到新位置后根据贪婪选择选取更优位置，并保留给下一代种群，跟随蜂共享采蜜蜂的信息后，通过概率分布函数来跟随采蜜蜂，如式（7）所示。

式中：TS为从个体空间S2到个体空间S1的随机映射，记TS：S2→S1；f为优化算法的目标函数；Xi+1为更新之后跟随蜂的位置。

4）在跟随蜂搜索阶段，根据采蜜蜂传递蜜源信给跟随蜂，通过式（7）计算选择跟随蜂的概率，随后，跟随蜂将确定出一个合理的采蜜地点进行进一步搜索，跟随蜂更新方式为

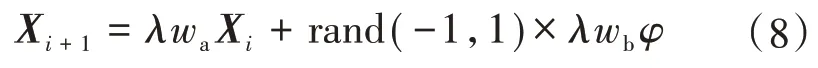
式中：l为一个动态变化的系数，当新位置适应度值比原位置好时，l大于1，反之小于1；φ为自适应因子；wa，wb为两个权重系数。j，wa，wb分别按式（9）—式（11）进行计算。

式中：tmax、tmin分别为算法要求的最大及最小误差；w1，w2，w3，w4为惯性权重，取值范围为［0.1，1.5］，且w1，w3小于w2，w4；I为当前迭代次数；Cm为最大迭代次数；a在［0.8，1］之间取值；b在［1，1.2］之间取值；φ为自适应因子。

5）若Xi经过多次迭代，或搜索到达最大迭代次数Cm后，蜜源的位置不再向更优的方向进行更新，则丢弃此蜜源，将雇佣蜂转回观察蜂。同时，观察蜂依照式（5）所表示的策略生成新蜜源Xi。

6）若在某次迭代过程中达到了算法收敛要求，则结束迭代过程，给出最终的可行解及适应度值，否则转回到2）继续搜索。

在ABC 算法执行结束后，输出该算法最后一次迭代的结果，并将其传递给SQP 算法作为初值进行二次优化，最后得出一个在全频段满足要求的精确解，确定出扩展德拜模型的所有组件参数值，完成油纸绝缘介电响应的参数化建模。

3.2 参数辨识结果及分析

为了验证上述方法的有效性，针对本文2.2节所实测的3 组35℃下不同绝缘含水质量分数（0.71%、1.10%、2.00%）的频域介电谱，运用上述所提出的方法进行了参数辨识，得出了扩展德拜模型各支路的组件参数值，如表1 所示。基于参数化之后的扩展德拜模型，可以得出根据模型重构出的FDS 谱图（拟合值），并同实测谱图进行对比，如图6所示。

图6 参数辨识后的模型重构谱图同实测谱图对比

表1 中的拟合优度指标显示，所确定的模型参数对FDS 结果的重建是准确的，3 组数据的拟合优度均达到了0.95 以上，表明本文所采用的扩展德拜模型及参数辨识算法能够实现在所测量的宽频范围内（10-4～103Hz 数量级）对介电响应谱图的精确建模。

表1 扩展德拜模型参数辨识结果

此外，值得注意的是，尽管算法中没有对这些变量施加明确的范围约束，但所有的电阻和电容计算值均分别位于109Ω 和10-9F 的数量级之内，该范围是目前公认的具有物理意义且合理的扩展德拜模型参数取值范围，符合文献报道中从PDC 或RVM 进行参数辨识所得的模型参数值范围［16-17］。综上所述，以油纸电容式套管为典型的油纸绝缘研究对象，基于频域介电响应数据及扩展德拜介电等效模型，采用一种改进的人被雇佣的蜜蜂群算法及SQP 序列二次算法的融合算法实现了在宽频范围内的扩展德拜模型参数辨识。

4 结语

基于扩展德拜模型对油纸绝缘套管的介电响应进行了等效建模研究。首先对套管模型进行了人工受潮实验，对制备的不同绝缘含水量的套管样本进行了FDS 测量。为了获得等效电路中的参数，采用了一种改进的ABC 同SQP 融合的算法进行参数辨识。建模结果表明，采用上述模型及算法进行建模，对实测FDS 谱图的拟合优度均达到0.95 以上，证明所采用的扩展德拜模型及参数辨识算法能够实现在所测量的宽频范围内（10-4～103Hz）对介电响应谱图的精确建模。下一步的研究工作是基于该模型及其参数，探究模型参数变化同绝缘状态变化之间的对应关系，以获得油纸绝缘状态的定量诊断依据。