基于码元同步环路的激光测距通信一体化算法优化研究

李梦思，谌 明，张 靓，李晓亮，李英飞

（北京遥测技术研究所 北京 100076）

引 言

随着空间技术的发展，航天任务日益复杂化，空间科学对星间测控、通信等方面提出了更高的要求。基于激光的通信测距一体化技术，将通信和测距技术融合，在通信带宽、测量精度、抗电磁干扰、设备功耗等方面具有突出优势，具有更好的环境适应性，可以满足日益复杂化和多样化的各类航天任务，是航天飞行器测控通信发展的重要方向。

早在1997 年，美国就提出了同时具有激光测距和通信功能的X2000 系统。2005 年，俄罗斯的GLONASS-K 卫星建立了国际首个星间激光链路，实现了测距精度达10 cm 的星间测距，通信速率为50 kbit/s，通信误码率优于10-4，链路建立最快时间小于10 s。为后续的通信与测距一体化技术提供了新的发展思路。随着星间激光链路技术的发展，基于码元同步技术的测距通信一体化技术成为激光通信测距一体化方案研究热点。2013 年，美国的月球激光通信星载终端在PPM 调制的激光链路上通过提取码元同步的相位实现了厘米级别的测距精度，充分展示了激光通信测距一体化的巨大潜力[1]。

目前，关于星间激光链路的通信理论得到了较为广泛且深入的研究[2-4]，而基于相同链路的测距理论分析较少。此外，关于激光测距通信一体化系统的实现形式、具体的融合算法、时频传递功能的进一步拓展等诸多技术问题都仍有较大的探索空间。为丰富激光测距通信一体化理论，寻求更高效、更优化的激光测距通信一体化方案，本文提出了基于Gardner 码元同步环路的通信测距一体化方案，这一同步处理算法在通信信号处理中仅需要2 个采样点即可还原出原始信号，且不受载波相位影响，适应相干和非相干调制体制，兼容高阶相位调制，适用于高速信号处理系统。本文根据环路跟踪原理，从理论上对测距通信一体化技术的测距方差进行推导分析，依据分析结果对鉴相算法进行优化设计，并通过仿真实验验证了优化算法的可行性。根据不同距离、信噪比下的仿真结果，分析了不同因素对测距结果的影响。

1 测距通信一体化原理

星间测距的本质是对目标间传输信号在空间中的飞行时间进行精密测量，从而解算出目标间的距离。在发射端的数据中插入测距标识，在接收端探测标识到达的时刻，通过时间差推算发射端到接收端的距离。得益于空间激光链路的通信编码原理，在一个双向双工的空间激光通信系统中，可以利用具有识别性的通信编码作为标识，如：与时钟整秒时刻对齐的帧同步头比特的下降沿作为标识等，便于接收端识别帧同步头以及记录标识到达时刻。

对于一般的非相干通信，接收端对所接收信号的处理原理如图1 所示。激光信号由光学天线进行收集，经过光电探测器转换为电信号，电信号经过AD 采样后进行载波、码元以及帧同步解码等处理后获取通信信息。同时，码元同步以及帧同步模块输出相应的参数，由测距模块进行相应的解算，获得距离信息。

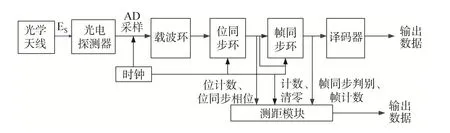
图1 激光测距通信一体化系统信号处理流程图Fig.1 The process of integration system of laser communication and ranging

具体而言，链路通信双方约定在某个帧（假设为第0 帧）同步头的信息流最后一个比特发射出去后开始记录当前的时间ts(t-)τ，在接收到相同的帧同步头（即另一端发射的第0 帧的帧头）最后一位后，记录下当前到达的时间tu(t)，读出数据中的整秒以及整帧的数据，同时，提取帧内同步的码元数以及码元同步的相位等高精度计时信息，与整秒信息一起进行高精度解算。最后根据所得的飞行时间，推算出所测距离为：

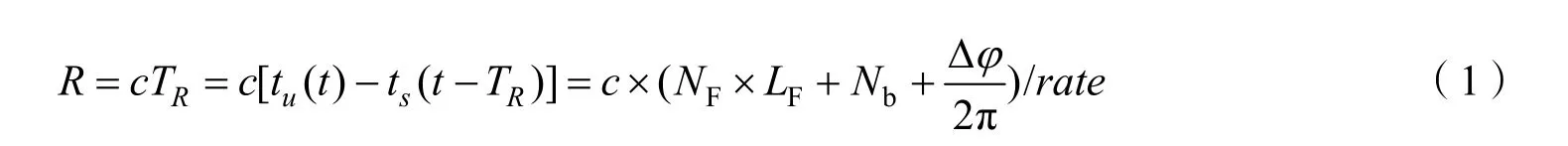
其中，c是光速，TR是光的飞行时间。NF是数据帧计数，LF是帧长，Nb是码元计数，Δφ是码元相位，通过码元同步进行提取，rate为码元速率。式（1）中，(NF×LF+Nb)/rate是一个整数项，代表着终端在发射测距标识到接收到相应的测距标识的过程中，终端处理码元总数所对应的时间，而Δφ则是标识与本地时钟对比时小于一个码元的相位值，这个值的提取相当于对码元周期进行了进一步的细分。在空间大范围的测距中，利用帧同步头所携带的信息，加入一定周期的帧计数和秒计数，可以拓展测量范围。最终通过信息识别以及脉冲计数可以简单有效地获取测距中的码元整数信息，其测量精度直接与时钟关联。从式（1）中可以看出，Δφ的提取精确程度决定了整个系统测距的精确程度。因此，本文重点对码元相位提取技术展开研究。

2 码元相位提取及算法优化分析

根据码元同步原理，为保证信号采样处于最佳判决时刻，需要对信息的时序与本地时序的差异进行校对，尽可能地识别每个码元信号的电平保持范围，并在合适的时刻进行采样。Gardner 算法通过判断信号零点位置，推算出最佳判别时刻。测距算法根据判别时刻的NCO（Numerically Controlled Oscillator）值来估算码元相位。如图2 所示，Gardner 同步环是由插值滤波器、定时误差检测器、环路滤波器以及NCO 组成。

图2 Gardner 插值同步环组成原理图Fig.2 The structure and principle of Gardner symbol synchronous ring

定时误差检测器检测输入信号XmTs的定时偏差，获得与定时误差成比例的误差信号en，误差信号经环路滤波器抑制噪声和高频分量，输出环路控制字Wn，NCO 根据控制字调整的输出内插控制信息mn和un，内插滤波器根据NCO 输出的控制信息调制输出采样时刻，最终由插值滤波器得到最佳采样时刻，得到输出ykTi。根据同步关系，可以得到所需的码元相位为：

其中，ChipNCO 是NCO 寄存器中保存的NCO 相位，作为码元相位的估算值。NCOword是码环NCO 的相位寄存器位数。

信号中的噪声是影响系统测距精度的主要因素。假设输入信号中的噪声是高斯白噪声，功率密度为N0/2，环路带宽为Bn，则根据环路跟踪原理，噪声导致的环路抖动为：

式中En为噪声经过鉴相器后的输出值，K为鉴相增益。由式（3）可知，最终探测到的码元相位抖动主要受到环路带宽以及鉴相算法的影响。对于高斯白噪声，环路带宽对噪声起到限制作用，带宽越小，噪声功率越小，环路抖动则越小，但是过小的环路带宽也会影响环路的动态跟踪性能，因此需要在设计时进行综合考虑。而鉴相算法相当于对噪声进行了一次变换，有。而变换的增益越高，最终误差抖动越小。根据经典的Gardner 算法，鉴相器的输出为：

利用离散自相关原理可以得到相应的鉴相函数S函数为[6]：

式中C为信号功率，Tm=1/rate是码元周期，为与基带成型带宽有关的系数，而β为基带成型滤波器的剩余带宽比值。Gardner 环路的鉴相函数具有sin 函数性质，相比于线性鉴相函数，sin 函数在零点附近具有更高的增益：

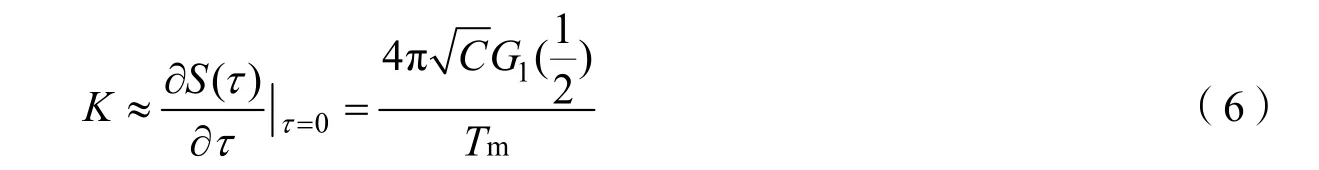
为了进一步提高鉴相增益，压缩噪声方差，本文对经典Gardner 算法进行了适当的改进。在式（6）中，若保持信号功率和码元速率不变，则成型滤波器的系数是影响鉴相增益的主要因素，成型滤波器系数与滤波器剩余带宽以及鉴相延迟间的关系如图 3 所示。可以看出，带宽要求不变时，有。而系数取G1(0)时，对应的鉴相函数为：

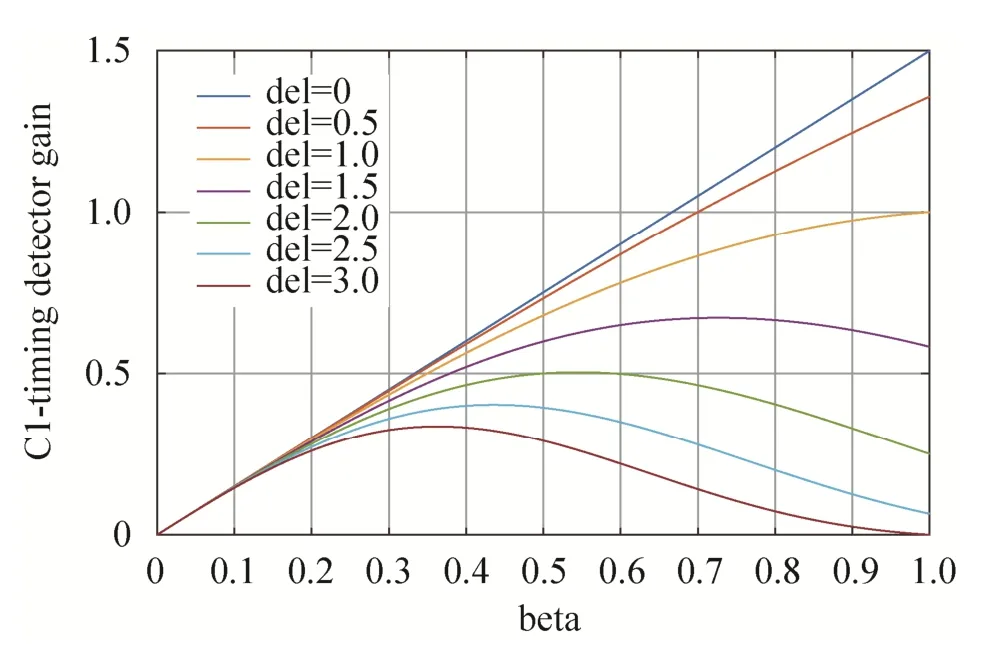
图3 成型滤波器系数与滤波器剩余带宽以及鉴相延迟间的关系图Fig.3 Timing detector gain with different Δ and β

然而这一函数值使用了一个符号采样的后半部分，这样一来如果NCO 初始相位偏离大于半个码元周期，则码元输出相位容易发生跳变，因此在进行同步时需要对初始相位进行判别和限制。最终得到相应的S 函数为：

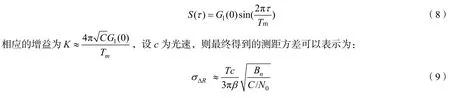
3 仿真分析

为了验证新鉴相算法相比于传统Gardner 算法所获得的误差压制效果，分别对Gardner 算法和改进算法得到的测距方差进行仿真分析。设码元速率为1 Gbps、基带额外带宽β=0.5，带宽为Bn=2 ×105Hz，换算得到对应的信噪比E0/N0=10 dB。改进鉴相算法用于距离解算以及通信解调的仿真结果如图4 所示。为确保仿真数据的可靠性，图4（a）中每个距离值的仿真均进行了200 次的重复实验，所得的结果为实验平均值，图4（b）为码元判别与原始数据的对比示意图。结果表明，鉴相算法的改进对通信判别结果没有产生影响，这一算法可以同时实现信号的码元同步功能和测距功能，且测距方差并不会随着距离产生明显的变化，影响测距精度的主要因素是环路的跟踪精度。通过调整环路带宽，获得在距离不变的条件下，对不同的E0/N0条件下的测距方差仿真结果如表1 所示，不难发现，环路的噪声对测距精度的影响较大。

表1 不同信噪比下的仿真结果Table 1 Jitter standard deviation simulation results in different SNR

图4 仿真结果图Fig.4 Results

图5 为改进前后两种判别算法所得的测量结果，在其他条件不变的情况下，原始的Gardner 算法得到的测距方差为0.806 mm，而改进的鉴相算法得到的测距方差为0.376 mm。对比表1 可以看出，改进的鉴相算法使得测距方差得到了明显的收敛，在相近的测距方差下，改进算法的噪声容忍度获得了近4 dB 的提升。

图5 算法改进前后测距仿真对比图Fig.5 Simulation comparison of distance measurement before and after algorithm improvement

综上所述，采用Gardner 码元同步技术可以同时实现对信号数据的最佳采样判决和高精度测距。测距精度受到环路和信号的多种参数影响，通过调整基带的成型滤波参数、降低同步环路带宽提高信噪比以及采用增益更高的鉴相算法等手段可以有效压缩测距抖动方差。不过，在具体的环路设计时，仍需要综合考虑实际项目背景以及通信技术要求，如小的环路带宽可以有效减小测距方差，然而环路带宽过窄则会降低环路动态性能等。

4 结束语

随着空间激光技术的发展，空间激光通信理论得到了蓬勃发展，随之兴起的激光测距一体化技术中关于测距的理论研究仍有较大发展空间。本文提出了基于Gardner 码元同步环路的测距一体化算法，该算法实现了测距和通信功能的高度集成。通过理论公式推导以及仿真实验，验证了改进算法的正确性，揭示了信号噪声、鉴相算法、环路带宽、基带成型滤波器参数等多个参数对测距精度的影响，丰富了测距通信一体化计数理论，为后续设计研究提供了仿真依据。