浅谈元认知策略在中学数学教学中的应用对策
2022-06-03张义朱丽卢格格
张义 朱丽 卢格格



摘 要:文章旨在探析元认知策略在中学数学教学中的有效应用。数学教师运用元认知策略进行一系列元认知训练活动引导学生自主学习。实践表明,元认知策略的有效运用大大促进了数学教学。
关键词:元认知;元认知策略;中学数学教学
中图分类号:G633.6 文献标识码:A 文章编号:1673-8918(2022)13-0071-04
一、 问题提出
我国著名学者李大潜强调数学学科本身和学好数学对学生成长均具有重要的作用。笔者作为一名从教多年的中学数学教师,当然懂得数学的重要性,那么教师如何施教才能使学生学会自主学习,为学生适应社会发展和终身发展奠定基础。中学数学教学一直以来存在难度,美国数学家克莱因认为主要原因在于部分教师对“学生怎样学习”方面缺少重视即对“元认知”的掌握不多或不够。那么,教师如何在教学中嵌入元认知成为一个重要议题。为此,笔者以元认知理论作为支撑,对近年来的一些有关文献进行研读,探索适于自身情境的元认知策略教学。
二、 理论基础
(一)元认知与元认知策略
“元认知”一词,通常被认为是美国心理学家弗拉维尔于20世纪70年代在其著作《认知发展》中首次使用的认知心理学范畴的词语,他认为“元认知”是“对认知的监控”,包括三个主要部分:元认知知识、元认知经验和元认知策略。简而言之,元认知,即认知的认知。元认知的诞生,有助于大家从更深层级理解学习者的学习过程。
一般情况,元认知通常被理解为包括元认知知识、元认知体验和元认知策略三个方面。元认知知识,是指学习者在认知活动中获取到的有关认知的一般性知识;元認知体验,是指学习者对同步于认知活动进行而产生的情感体验或感悟;元认知策略,是指学习者对自己的认知活动过程的计划、监控、修正、调节与反思而采取的学习策略。其中,元认知策略属于三者中最重要的组成部分,Schraw和Moshman认为元认知策略至少包括计划、监控和评估三个环节。文章中的元认知策略主要是指学生制定学习计划、定位学习目标、监控学习全程、反思评价学习效果等具有内部逻辑关系的一系列过程。在教育教学领域,尽管众多国内外研究学者对元认知策略无统一定义,但他们对元认知策略内涵的挖掘是趋于一致的:更好地帮助学习者更有效地学习。
元认知和元认知策略之间相互影响、相互交融、不可分割,共同作用于学习过程。
(二)元认知在中学数学教学中的重要作用
南京师范大学喻平教授梳理了国内外的一些元认知研究得出总结:(1)数学问题解决中存在元认知因素;(2)元认知训练可以提高问题解决能力和解题水平,正向影响学生学习;(3)元认知策略对数学解题有显著影响;(4)中学数学教学中应该将这些元认知的研究成果应用于中学数学教学中,重视元认知策略对教学的重要价值。此外,西南大学张庆林教授对小学六年级的学生运用四种形式不同的应用题进行元认知监控测试,结果证明加强对学生的元认知监控训练可以有效提高学生理解和分析应用题的能力。童世斌等人对中学生进行思维策略训练的基础上配以元认知训练,结果表明元认知训练能够大大有助于提高解答数学应用题思维训练的效果。Mevarech把174名七年级的以色列学生分为元认知训练组、策略直接指导组和控制组进行有关数学问题解决的笔试,最后成绩结果显示元认知训练组明显优于其他两组,此研究说明元认知训练组的学生通过教师的引导能够从问题全局着手,进一步分析具体问题的上下文情境,通过过程监控发现解决问题时出现的不足并及时调整寻找更为优化的问题解答方法。北京师范大学董奇教授利用实验研究方法证明了元认知与思维品质之间存在因果关系,即元认知的改变必然引起思维品质的改变。
结合以上国内外知名学者的相关研究,充分说明元认知策略对中学数学教学的促进作用。
三、 数学教学嵌入元认知策略
(一)理论依据
在此我们主要参考Hartman和Sternberg(1993)在元认知教育应用研究中提出的四种主要的元认知训练方法作为展开数学教学的理论依据:
(1)教师善用元认知策略的通俗表达用以提高学生利用元认知策略解决数学问题的意识;
(2)丰富学生在数学信息表征方面的元认知能力;
(3)注意培养学生元认知计划、监控、反思习惯;
(4)创设有元认知策略促进学习的环境。
(二)元认知训练的具体应用说明
(1)在第一种训练方法中,教师结合实际教学把元话语用通俗易懂的表达使学生理解元认知训练目的和方法。例如,在具体讲述解题过程中需要说明哪些心理活动参与其中,反思题目类型与实质;在解决较难问题时,提醒学生仔细审题、重复读题、认真思考解题突破口,在训练中要注意引导学生领会“把数学知识学‘活’、学‘透’”“解题过程真正搞懂,解题结果自然基本不错”“转一转、换一换、变一变、化一化、画一画”等课堂话语的真正含义。在此一定注意要把元认知话语转化成通俗易懂的表达来实施训练。
(2)在第二种方法中,教师通过不断地学习元认知理论丰富自我的同时,也要与学生建立元认知共同理解,一起总结适合数学学习的元认知策略引领学生善用元认知策略并验证策略是否真正有助于数学学习,不断积累有效解题方法;在面对难题时,提醒学生放慢语速解读题目信息,准确提炼数学表征,通过数形结合、列方程、分类讨论、化归、转化、整体性等数学思想进行内化求解、或可视化求解、或建立图表求解等。这种训练有助于提高学生分析问题信息所要表达的数学表示的能力。
(3)第三种方法强调培养学生的自我监控能力,教师引导学生根据个人因素、任务难度设计学习计划与目标,善于发现学生的兴趣点与当前任务之间的相关性,激发学生对解决目前任务的好奇心,聚焦学生对教师提问的思考。通过师生对话明晰学生的解题思路,基于学生解题思路视角发现解题困难出现的共性、原因与特点,不断反思教学过程中的课堂话语是否能被学生充分理解,真正做到“以生为本”。加强元认知监控训练是提高学生理解力和分析力的有效途径。
(4)第四种方法要求教师加强创新性教研意识,不断探索运用元认知策略进行施教的科学方法与学习的人文环境,提升学生自主学习能力,向学生指出能力提高的归因是有效地使用了元认知策略。
四、 调查方法及其分析
(一)参与者
参与文章次元认知策略教学实践的是一所县实验中学的初中二、三年级全体学生,共323人,其中男生有175人,女生148人,男生占54.18%,女生占45.82%。这些学生数学学习成绩平均水平位列全县中层水平,用发展的眼光来看,他们具有很好的学习潜质。
(二)问卷设计及其数据分析
1. 问卷设计说明
最近发放的调查问卷内容如表1所示,分享发放日期选择在周末以便学生居家使用手机根据自身体验进行作答。问卷由24个题目组成,其中1、2题属于基本信息题,实际需要作答的有22道题:3~8题为元认知计划策略问题,9~17题为元认知监控策略问题,18~24题为元认知反思评价策略问题;每题选项采用李克特5级量表,将定性指标分成1~5个档次(完全不这样、不这样、偶尔这样、经常这样、总是这样),分别赋值1,2,3,4,5。根据此次调查收集到的问卷数据进行了简单分析。
2. 数据分析
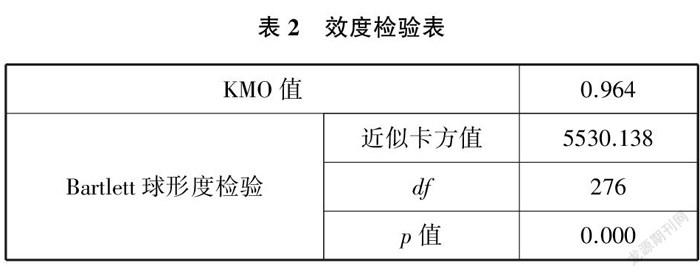
①首先分析问卷效度,效度分析用于研究量表题的设计是否合理、是否有意义。分析结果见表2所示:
表2中的KMO数值用于判断信息提取的适合程度。若此值高于0.8,则说明研究数据非常适合提取信息,效度非常好;若介于0.7~0.8之间,则适合提取信息,效度较好;若介于0.6~0.7之间,则比较适合提取信息,效度一般;若小于0.6,不适合提取信息,效度不好。而表2中的KMO=0.964,说明问卷数据非常适合提取信息,问卷设计有效。
②分析问卷信度,信度分析用于量表题回答的可靠性、准确性。分析结果见表3所示:
表3中的Cronbach α系数表示信度的高低,若此值高于0.8,则信度高;若介于0.7~0.8之间,则信度较好;若介于0.6~0.7之间,则信度可接受;如果此值小于0.6,说明信度不佳。而表3的信度系数值为0.959,大于0.8,说明问卷信度质量很高:学生真正意识到了元认知策略之于数学学习的重要性。
③对问卷数据的基础指标进行描述性分析,此分析用于整理问卷中各题整体平均得分情况,结果见图1:
图1 问卷基础指标数据图
问卷各题均是单选题,每题的五个选项均为:A——完全不这样、B——不这样、C——偶尔这样、D——经常这样、E——总是这样,将A~E五个档次依次分别赋值1,2,3,4,5,若同一问题所有人全部选择A项,则本题整体得分平均值为1,最小值和最大值也均为1,若同一问题所有人全部选择E选项,则本题整体得分平均值为5,最小值和最大值均也为5。由此可知,每题基础指标数据的最小值为1,最大值为5,因此每题整体平均得分一般介于1~5之间。
本次问卷各题的基础指标数据如图1所示:从右往左来看,每题的整体得分平均值依次按照从高到低排列,得分越高说明该题的元认知策略在学生的学习过程中运用的人数越多、作用越大、认可度越高,对学习越有帮助。
从图1可以看出,问题12、13分别排位第一、第二,属于监控策略,这种结果与许多研究强调的“元认知监控策略是元认知策略中最重要的策略”相一致;问题4、24、5分别排位第三、四、五,其中问题4、5属于计划策略,问题24属于反思评价策略,这种结果说明了元认知计划策略在教学中的地位与作用,同时反思评价策略也不可忽略。
五、 启示
初中数学教学中应用元认知策略的尝试与实践,是一种挑战也是一种创新,丰富了元认知策略促进教学的理论,监控策略在元认知策略中的重要作用尤其显著,但计划和反思评价策略不可或缺;元认知策略在数学教学中的应用,不仅促进了数学教学,也明显提高了学生自主学习的能力且充分挖掘了学生自我管理的潜质。
笔者尝试将元认知策略应用于数学教学之中。实践表明,元认知策略的运用既有助于教师教育基础知识的掌握和专业发展水平的提高,又有助于学生创新思维的发展,特别是极大地鼓励了后进生的学习信心与积极性,助力全体师生共同提高,凝聚教学相长的班级文化氛围。在课程与教学改革的新时期,文章对设计融合元认知策略教学的应用与环境,具有重要的现实意义。
参考文献:
[1]李大潜.谈谈中学阶段的数学学习[J].新课程评论,2018(5):7-20.
[2]Flavell J H. Metacognition and cognitive monitoring: A new area of cognitive-developmental inquiry[J]. American Psychologist,1979.
[3]Schraw G, Moshman D. Metacognitive theories[J]. Educational Psychology Review,1995,7(4).
[4]王众,喻平.问题解决中元认知的心理学研究及其对中学数学教学的启示[J].教育研究与评论(中学教育教学),2020(1):24-29.
[5]张庆林,管鹏.小学生表征应用题的元认知分析[J].心理发展与教育,1997(3):13-16.
[6]童世斌,张庆林.元认知训练对提高中学生解答数学应用题能力的实验研究[J].心理发展与教育,2004(2):62-68.
[7]Mevarech Z R. Effects of Metacognitive Training Embedded in Cooperative Settings on Mathematical Problem Solving[J]. The Journal of Educational Research,1999,92(4):195-205.
[8]董奇.元认知与思维品质关系性质的相关、实验研究[J].北京师范大学学报,1990(5):51-58.
[9]Hartman H, Sternberg R J. A broad BACEIS for improving thinking[J]. Instructional Science,1993,21(5):401-425.
[10]周俊.問卷数据分析:破解SPSS的六类分析思路[M].北京:电子工业出版社,2017.
作者简介:张义(1979~),男,汉族,山东滨州人,山东阳信县第五实验中学,研究方向:数学教育;
朱丽(1979~),女,汉族,山东滨州人,山东滨州市实验学校,研究方向:元认知等高阶思维、科学传播、科学教育;
卢格格(1994~),女,汉族,新疆昌吉人,新疆乌鲁木齐市第126中学,研究方向:数学教育。
