基于K-D 树加速的大型点云配准算法

吴振慧，王彩余

（1. 扬州市职业大学 电子工程学院， 江苏 扬州 225009； 2. 扬州广润机械有限公司 技术部， 江苏 扬州 225000）

在工业生产领域，尤其是自动化装配和生产领域，受测量方式和被测物体集合形状的限制，对于同一物体，需要在不同视角下扫描得到两组或多组不同的点云数据。为了计算在此过程中物体或设备的运动，或是进行点云拼接，都需要找到两个点云之间的对应空间位置关系，进行点集与点集坐标系间的转换，实现配准，可见点云配准至关重要。

从物理学角度分析，点云配准即为计算源点云和目标点云之间的旋转矩阵R 和平移矩阵T，通过这两个矩阵即可描述三维空间中两个点云的相对位置关系[1]。为了提高点云对于物体的描述精度，目前的扫描仪通常采用小点间距、小线间距的阵列式扫描。对于同一物体，越小的点、线间距意味着扫描出的点云中包含的点数据越多。然而，针对大型点云数据，其配准算法要在保证精度的基础上，提高其速度，若采用一般的配准算法，计算耗时非常大，难以在工业界使用。因此，本文提出基于迭代最近点（Iterative Closest Point，ICP），结合预处理和K-D 树的大型点云配准算法，以期在满足精度要求的同时，提高计算速度。

1 迭代最近点算法

1.1 迭代最近点算法步骤

迭代最近点（ICP）算法[2]是目前使用最广泛的点云精配准算法之一。ICP 算法的核心步骤为：在目标点云（Target）中寻找源点云（Source）的最近点，通过找到的对应最近点，使用最小二乘法构建目标函数，计算参数矩阵R 和T，经过一步计算后，将源点云进行R 和T 的位移变化，再次寻找最近点，如此迭代直到目标点云和源点云的距离小于阈值。

ICP 算法的目标函数如下：

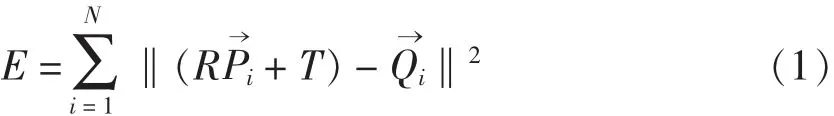
ICP 算法的步骤如下：

第一步，在目标点云 Q 中计算源点云 P（k）中每一点的最近点，k 表示迭代次数。

第二步，计算能使得P（k）和其对应最近点标准误差E 最小的旋转矩阵R 和平移矩阵T，其标准误差计算依据公式（1）。

第三步，使用第二步中计算得到的旋转矩阵R 和平移矩阵 T，移动 P（k）使其成为 P（k+1）。

第四步：如果 P（k+1）和 Q 之间的标准误差 E 小于阈值，则迭代停止，否则重复第一步至第三步。

1.2 迭代最近点算法计算方法

迭代最近点算法的主要问题在于：（1）如何在目标点云Q 中寻找源点云P（k）中某一点对应的最近点；（2）如何根据一一对应的最近点，计算得到旋转矩阵R 和平移矩阵T；（3）如何将每一步计算得到的旋转矩阵和平移矩阵合成为一个参数矩阵。

1.2.1 最近点的计算

针对问题（1），如果点云数据量较小，可以采用暴力搜索的方式寻找最近点。然而，针对大型点云该方法会消耗大量时间，并不适用。针对此，本算法采用了去质心和降采样的预处理方式。去质心即在计算开始时，将点云的坐标分别减去其质心坐标，保留相对位置，以大大减少搜寻最近点的时间。过多的对应点对于计算准确性的提高作用甚微，只需采集少部分的特征点即可进行计算，故本文采用读取点云后即进行30 %的降采样操作方式，随机均匀删除70 %的点，在进行计算时，还可人为或随机选取更小一部分的特征点作为迭代依据。因此，公式（1）可转化为：

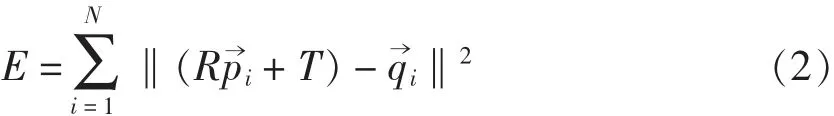
其中：p 表示源点云P 中被选择作为特征点的点云，称为特征源点云；q 表示目标点云Q 中与p 对应的最近点，称为特征目标点云。

要注意的是，在计算旋转矩阵R 和平移矩阵T 时，可以仅使用很少一部分的特征点，但在判断迭代是否停止时，需要对所有点求其平均标准误差E。公式（2）中的N 不是源点云所有点的个数，而是特征源点云所有点的个数。

1.2.2 参数矩阵的求解

奇异值分解算法计算效率高，计算结果准确，是针对问题（2）的经典计算方法。因此，本算法采用奇异值分解的方式并依据公式（2）求解目标函数，具体计算过程如下：

第一步，计算两部分特征点云的质心：

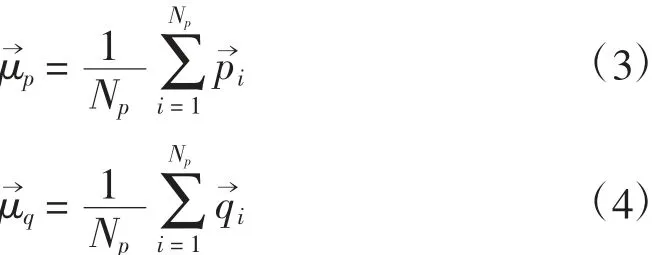
第二步，去质心化：

第三步，构造协方差矩阵H：

第四步，使用奇异值分解矩阵H，得到U、S、V：

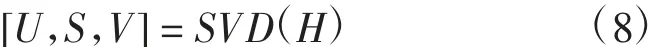
第五步，计算旋转矩阵R：

第六步，计算平移矩阵T：

然后，更新特征源点云p 和源点云P 中所有点的坐标：

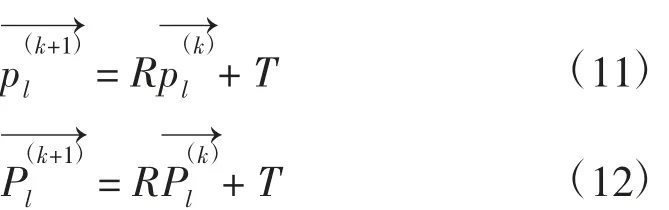
至此，完成一步迭代。当标准误差E 小于阈值时，迭代停止，配准结束。根据工业现场定位要求，阈值设置为0.5 mm。

1.2.3 点云坐标的齐次化

针对问题（3），参考运动学原理[3]，可以引入齐次坐标，通过齐次变换矩阵M 统一表示旋转矩阵R 和平移矩阵T，

此时，一个三维空间的坐标表示为齐次坐标的形式，

可以发现齐次坐标变化公式（15）与笛卡尔坐标变化公式（12）等价，

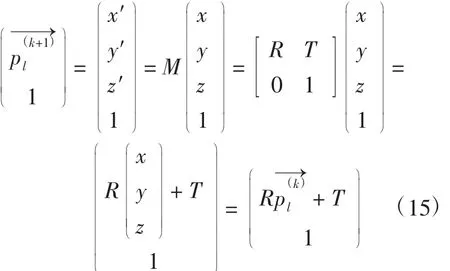
根据点云绕固定坐标系的齐次变换是齐次变换矩阵的顺序左乘的定理，可以得到最终的齐次变换矩阵为：

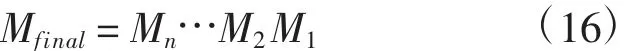
这里Mi表示第i 次迭代计算得到的齐次变换矩阵。

2 最近点搜索加速方法

针对大型点云配准的场景，传统ICP 算法的弊端在于，即使采用了去质心、降采样的预处理方式，如果对于每一个特征源点云中的点，都采用暴力搜索的方式寻找最近点，也需要多次遍历目标点云的所有点。针对这一弊端，杨秋翔等人基于法矢夹角对ICP 算法进行了改进[4]，杨小青等人基于法向量进行了改进[5]，朱玉梅等人提出基于DNSS 与点到平面的ICP 结合的方法[6]。考虑大型点云配准这一场景，本文采用K-D 树方法加速最近点的搜索。

2.1 K-D 树算法原理

K-D 树是K-Dimensional 树的简称，即为K维空间的树，是一种对k 维空间的点储存一遍从而可以进行快速搜索的树形数据结构[7]。K-D 树主要应用于多维空间中的最邻近搜索和范围搜索。K-D 树中每个结点数据类型描述见表1。

表1 K-D 树结点数据类型

2.1.1 K-D 树的构建

K-D 树的构建过程如下：

输入：k 维空间数据集 T={x1，x2，…，xN}，其中

输出：K-D 树

（1）开始：构造根结点，根结点对应于包含T的k 维空间的超矩形区域。选择x（1）作为切分的坐标轴，以T 中所有数据x（1）坐标的中位数作为切分点。分割超平面通过切分点并与坐标轴x（1）垂直，将根结点对应的超矩形区域切分为两个子区域，即根结点的左树Left 和右树Right。左树对应坐标x（1）小于切分点的左子空间，右树对应于坐标 x（1）大于切分点的右子空间。

（2）重复：对深度为 j 的结点，选择 x（l）作为切分的坐标轴，l=j（modk）+1 即为Split，以该结点的区域中所有数据x（l）坐标的中位数作为切分点。分割超平面通过切分点并与坐标轴x（l）垂直，将该结点对应的超矩形区域切分为两个子区域，即该结点的左树Left 和右树Right。左树对应坐标x（l）小于切分点的左子空间，右树对应于坐标x（l）大于切分点的右子空间。

（3）停止：直到结点的左树和右树没有数据时，分割停止，K-D 树形成。

K-D 树构建的时间复杂度为 O（log2n），并且对于迭代最近点算法，仅需要在第一次迭代之前构建K-D 树即可，无须在每次迭代中反复构建，因此其构建时间对于算法的整体时间影响很小。

2.1.2 K-D 树查找最邻近结点

K-D 树查找最邻近结点，即完成ICP 算法中在目标点云中查找源点云中的点对应最近点的过程，其查找过程如下：

（1）从根结点开始，判断输入点（即源点云中的点）与该根结点的位置关系，如果其x（l）坐标小于根结点的x（l）坐标，说明输入点在根结点的左树，则进入左子结点；如果其x（l）坐标大于根结点的x（l）坐标，说明输入点在根结点的右树，则进入右子结点。

（2）重复步骤（1）不断下移，直至移动到叶结点，将该叶结点作为“当前最近点” 。

（3）从“当前最近点” 上移，对于每个经过的结点，进行如下操作：①如果该结点比“当前最近点” 更接近输入点，则将其变为“当前最近点” ；②如果该结点另一侧子结点有更近的点，则进入其另一侧子结点并不断向下寻找。

（4）当搜索回到根结点时，搜索完成，找到最邻近结点。

2.2 K-D 树算法举例

为了直观地展示K-D 树搜索临近点的过程，图1 给出了一个二维平面上K-D 树的构建实例，其中包含 6 个点 （2，3），（5，4），（9，6），（4，7），（8，1），（7，2）。

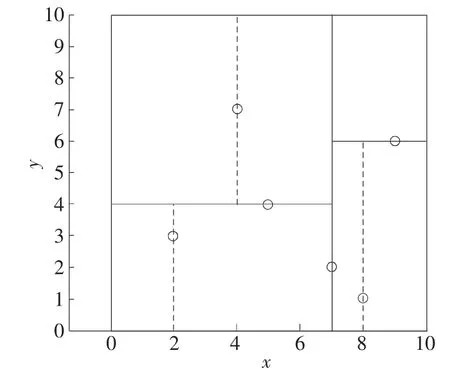
图1 K-D 树的构造

假设输入的点为（2，4.5），该点标注如图2，需要在上述6 个点中寻找与其最近的点。

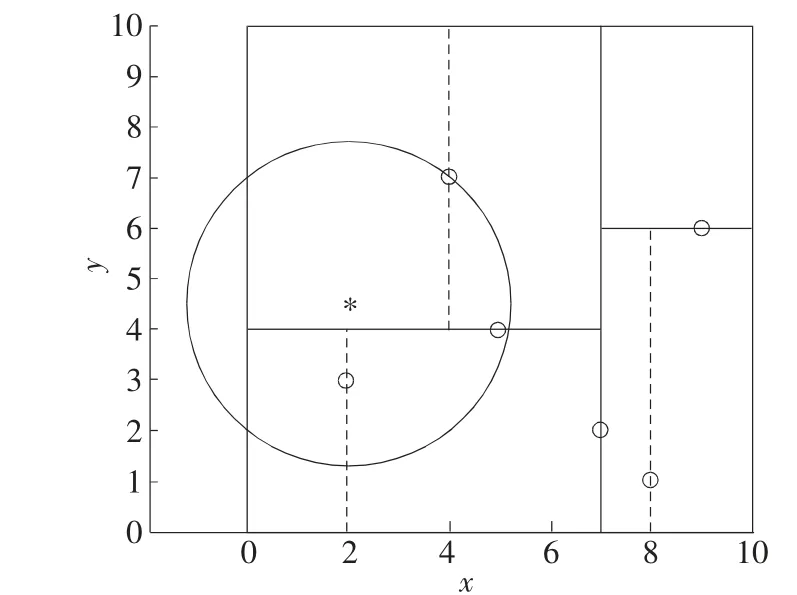
图2 输入点空间位置（星号位置）

首先，从根结点（7，2）开始搜索输入点（2，4.5），其过程是：

（1）输入点X 值2 小于根结点X 值7，因此访问左树，当前结点是（5，4）。

（2）输入点Y 值 4.5 大于当前结点 Y 值 4，因此访问右树，当前结点是（4，7）。

（3）当前结点已经是叶结点，向下搜索过程结束。

此时记录搜索路径为＜（7，2），（5，4），（4，7）＞，然后需要上移回溯搜索路径：

（1）回溯到（4，7），“当前最近点” 设置为（4，7）。计算（4，7）到输入点（2，4.5）的距离为 d1，图 2 中圆圈的半径即为d1。

（2）回溯到（5，4），由于（5，4）到输入点（2，4.5）的距离d2小于d1，因此“当前最近点” 更新为（5，4）；另外，由于输入点到（5，4）分割线的距离小于 d1，说明（5，4）的另一侧也需要查找，添加其另一侧的点（2，3）后，搜索路径变为＜（7，2），（2，3）＞。

（3）回溯到（2，3），由于（2，3）到输入点（2，4.5）的距离 d3小于 d2，因此“当前最近点” 更新为（2，3）。

（4）回溯到（7，2），由于（7，2）到输入点（2，4.5）的距离d4大于d3，因此“当前最近点” 无须更新；另外，由于输入点到（7，2）分割线的距离大于d3，说明（7，2）的另一侧无须查找。

（5）所有搜索路径上的点均被回溯，回至根结点结束，（2，4.5）的最近点输出为（2，3）。

最近点搜索结果如图3 所示。

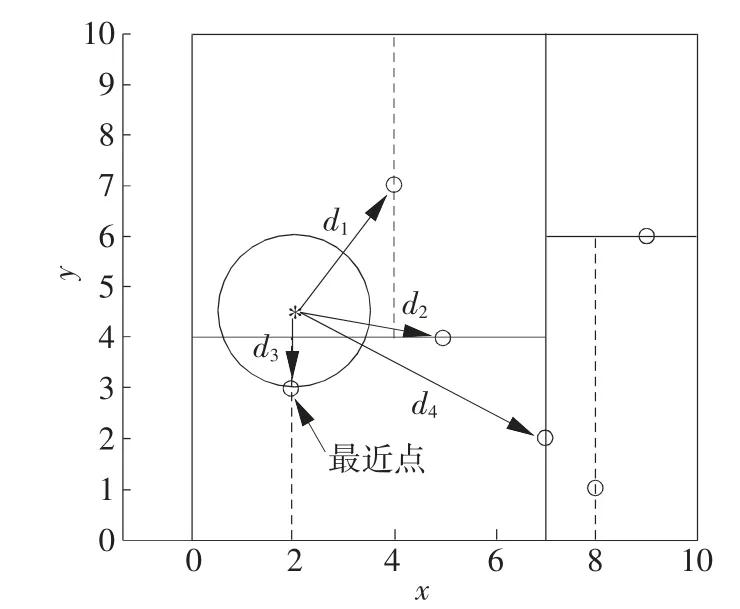
图3 输入点和其最近点

3 实验结果与分析

本文算法采用C++语言编写，在Visual Studio 2015 中编译和运行，采用OpenGL 三维图像库进行可视化交互。在此界面中，可以自由调整视角、缩放物体及框选物体上的点作为特征点等，并且程序可判断所选取点是否可见。本算法认为框选区域中仅正面可见的点为选择的特征点。

本文选择工业零部件的扫描点云作为实验数据，目标点云和源点云均以txt 文件形式存储，存储形式为：以v 开头的行表示一个点（Vertex）的三维坐标，以f 开头的行表示一个三角面片（Face）顶点的编号。点云文件的存储示例如图4所示。

图4 点云文件存储形式

读取点云文件后，以计算机图形学中典型的Half-Edge 结构进行点云模型的存储。在Half-Edge 结构下，可以很方便地遍历一个点的临近点和临近边，Half-Edge 结构如图5 所示，其中，每个“半边” 有对应的start（起始点）、twin（孪生边）、next（下一条边）、previous（前一条边）、left face（左侧边）。通过这种数据结构即可构造完整的点云模型。

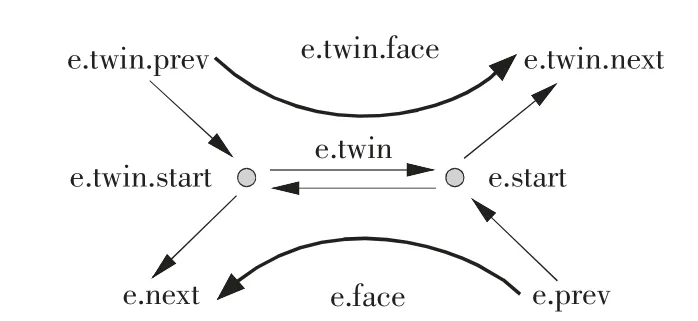
图5 Half-Edge 数据结构

读取并显示目标点云和源点云模型如图6 所示。图6 显示其形状几乎一致，但位置相差甚远。

图6 目标点云和源点云模型

源点云信息输出如图7 所示，其中包括顶点个数（453 089）、边个数（1 350 160）、面个数（895 959）等。由于其顶点个数多达45 万余，属于大型点云，符合本算法的使用范围。

图7 源点云相关信息

由系统随机选取 3 000、1 000、500 个点作为特征点进行计算，或手动选取如图8 所示的特征点，其实验结果如表2 所示。表2 中序号4、5 对应的特征点即为图8 中左右选择的区域。

图8 手动选取特征点（白色区域）

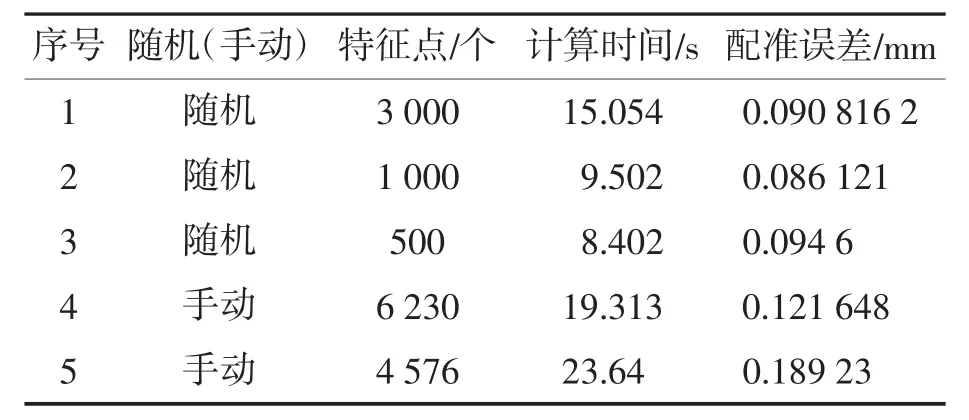
表2 实验结果

从表2 不难发现，采用系统随机选择特征点的方式，可以在使用更少的特征点，减少计算时间的前提下，保证配准误差小于0.1 mm。若采用手动选取特征点，由于点云数目众多，容易选取较多的特征点，因此计算时间较长。同时，因为选取的特征点分布较集中，所以误差比随机选择特征点时大，与本算法原理相符。但不论是随机还是手动选择特征点，都能保证在30 s 内完成误差小于0.2 mm 的配准，速度和精度均满足工业要求。

为验证采用K-D 树加速的优越性，本文将其与传统的一一暴力搜索最近点的方法进行精度和速度比较。原点云数目高达45 万多，本文降采样后在仅有1 万点左右的稀疏点云上进行传统的ICP 配准。选取所有点作特征点，完成配准的计算时间为24.94 s，配准误差为0.075 mm。由此可见，基于K-D 树加速的ICP 配准算法，能够在保证配准精度的前提下，大大提高ICP 算法的配准速度，是适用于大型点云配准的可靠方法。

4 结 论

本文基于ICP 算法，结合各种预处理方式和K-D 树数据结构，提出了针对大型点云的配准算法。该算法解决了传统ICP 算法不适用于大量数据计算的弊端，在保证计算精度的前提下，大大提高了计算速度，并且可视化界面交互性强，可以实时显示点云模型和配准结果。大型点云数据的配准实验表明，该算法鲁棒性强，速度灵敏，精确度高，可用于工业现场。