基于速率-状态摩擦定律研究剪切应力扰动对地震断层演化的影响
2022-06-02高雅琪史保平
高雅琪, 史保平
1 中国科学院大学地球与行星科学学院, 北京 100049 2 中国地震局第一监测中心, 天津 300180
0 引言
地震成因机制研究是现代地震科学所面临的一个重要挑战(National Research Council,2008;Lay et al.,2009).近几十年来对于触发地震和诱发地震的研究也已成为地球物理学的一个重要领域(Dieterich,1994;万永革等,2002;Ellsworth,2013;Brodsky and van der Elst,2014;Shapiro,2015; 解朝娣等,2021).因此,深入了解触发地震的摩擦力学过程对于现代地震危险性评估和地震预测有着重要的应用价值和科学意义.对于发震断层的应力扰动形式以及所对应的断层摩擦滑移响应的理解也成为我们深入探讨断层时空演化机制一个有意义的课题,速率和状态相关的摩擦定律(Dieterich,1992, 1994;Marone,1998)则成为当前定量了解地震触发机制一个重要组成部分.
由于地震活动的复杂性,当地壳内部出现不同时空尺度的应力变化时,应力跃变和依赖于时间的应力对发震断层的加载,处于不同演化时期的断层滑移和滑移速率将会受到不同程度的扰动,进而可改变原来的断层演化进程.影响区域地震活动性出现变化的应力扰动主要可分为两种:1)静态应力扰动;2)动态应力扰动.针对静态扰动模型,前人已建立了比较完善的物理模型并用于对区域地震活动性变化的阐述(Gross and Kisslinger,1997;Gross and Bürgmann,1998;Toda et al.,1998,2012;Dieterich et al.,2000;Perfettini et al.,2003a;孙楠等,2014).针对动态扰动模型,主要的研究则侧重于周期/非周期应力扰动对断层失稳的探讨(Heki,2003;Perfettini et al.,2003b;Cochran et al.,2004;Bollinger et al.,2007;Christiansen et al.,2007;Bettinelli et al.,2008;Ader and Avouac,2013;van der Elst et al.,2013;孙楠等,2014; van der Elst and Savage,2015;Yoshida,2018;Yoshida et al.,2020).近期的研究则扩展到由地表及近地表应力加载变化同区域地震活动相关性等方面的探讨,例如,由水文循环(Heki,2003;Christiansen et al.,2005,2007;Bollinger et al.,2007;Bettinelli et al.,2008;Ellsworth,2013;Kundu et al.,2015)引起的季节性应力变化同地震活动的关联性.喜马拉雅山地区季风与温度的变化会所引起当地水文的变化,如湖水增加和减少相当于地表应力的加载和卸载作用.Ader和Avouac(2013)则进一步分析了这样的准周期性载荷同区域地震活动的关联性.此外,人类活动如油页岩开采过程中地下注水引发的地下孔隙压力的变化,从而形成近地表应力加载的准周期性变化,亦可诱发地震活动(Shapiro,2015).同样,潮汐、固体潮等周期性载荷对地震触发的可能影响也为大量学者所研究(Wilcock,2001;Tanaka et al.,2002;Beeler and Locker,2003;Cochran et al.,2004;冯向东和魏东平,2007;吴小平等,2009).
目前,应用最广泛的状态演化定律分别是由Dieterich和Ruina提出的(Dieterich,1979a,b;Ruina,1983),可以用于解释岩石块体接触面摩擦过程的复杂行为.由于在实际应用时所具有的优缺点(见下文原理部分的阐述),许多学者都对这两个方程进行了必要的修正.但是,一致的状态变量演化的数学形式仍然是一个尚未解决的问题.实际上,现有的状态演化方程没有一个能与实验数据完全吻合(Beeler et al.,1994;Marone et al.,1995;Bayart et al.,2006;He and Wong,2014).Nagata等(2012)在状态演化方程中引入了应力速率项,给出了修正后的Dieterich演化定律.近期的研究结果表明,Nagata定律综合了Dieterich和Ruina定律的优点,使断层模型在对正、负向扰动的响应具有对称性的同时,又能表达断层愈合过程(Bhattacharya and Rubin,2014).Nagata演化定律已应用于对断层成核过程、断层演化及余震发生率模型等多个领域的数值分析研究(Kame et al.,2013a,b,2015; Bhattacharya and Rubin,2014),Yoshida等(Yoshida,2018;Yoshida et al., 2020)则采用该定律探讨了高频地震波作用下的地震动态触发机制.本文采用1D弹簧-滑块模型,从Nagata演化定律出发,进一步探讨静态应力扰动和周期性应力扰动,尤其极高频应力扰动对断层演化过程的影响.我们将介绍当前研究的基本原理,展示静态应力扰动和周期性应力扰动下的断层演化过程的区别,分析应力扰动量大小及扰动频率等因素对断层失稳时刻、地震重复发生周期的影响.
1 原理
本文采用1D弹簧-滑块模型来类比真实断层,该模型由弹性的弹簧和刚性的滑块组成.根据弹性理论给出的应力-应变关系,断层内部的剪切应力可以表示为:
τd=τin+τload-kδ-V,
(1)
公式(1)中,τin为断层内部的初始应力或剩余应力;τload为外部加载于断层面的剪切应力,可为一依赖于时间的函数;δ和V分别是滑块的滑动位移和速率(V=dδ/dt);k=ηG/l为刚度系数,其中G为断层面的剪切模量,l为断层的特征尺度,η为描述断层或裂纹几何状态的参数,与真实断层面的几何形态有关(Ruina,1983;Dieterich,1992,1994;Scholz,2002;Segall,2010),其取值一般近于1(Dieterich,1992;Marone,1998);=G/(2CS)为辐射衰减系数(Rice,1993),其中CS表示剪切波速度.对于地壳内部发震构造而言,最简单的设定是板块驱动所形成的恒定剪切应力速率加载,即外部剪切应力加载仅由远场板块运动引起:
(2)

(3)
公式(3)中,Δτ0表征静态扰动的方向(正向或负向)和大小,H(t)为阶梯函数.与静态扰动相对应的是动态扰动.进而,公式(3)可改写为:
(4)
公式(4)中,f(t)表示一般应力随时间变化的函数.在目前的工作中,我们仅考虑f(t)=Δτ0sin(ωt)下的周期性扰动的情形.其中,Δτ0表征简谐扰动的振幅值,ω为角频率.
断层的摩擦强度τf可表示为:
τf=μσ,
(5)
公式(5)中σ为有效正应力;μ为摩擦系数,可由RSF定律表达(Dieterich,1979a,b;Ruina,1983):
(6)
公式(6)中,μ为摩擦系数,V为滑移速率,θ为状态变量,V*是参考速率,μ0是当V=V*时的摩擦系数.a是直接影响系数,决定由速度变化引起的摩擦变化;b是演化影响系数,决定由状态变化引起的摩擦变化;DC是特征滑移距离.在断层的演化过程中,加载剪切应力τd与摩擦剪切强度τf须保持相等.
仅用公式(6)描述断层摩擦是不完整的,它只说明了摩擦同速度和状态的关系,还必须规定状态变量如何随时间或滑移速率变化,即所谓的状态演化定律.目前,应用最广泛的两个演化方程为(Dieterich,1979a,b;Ruina,1983):
(7)
(8)
公式(7)称为Dieterich演化定律;而公式(8)则称为Ruina演化定律.它们能够定量地描述断层面上的摩擦性质,从物理上阐明断层内部摩擦的复杂性.然而,二者都不能与岩石实验结果完全一致(Beeler et al.,1994;Marone et al.,1995;Kato and Tullis,2001;Bayart et al.,2006;Nagata et al.,2012).
近期,基于实验数据,Nagata等(2012)通过将实验获取的剪切应力和滑动速度代入本构关系的方法,计算了RSF定律中状态变量的值,其结果与上述两种演化定律的预测结果存在系统偏差.为此,他们提出了一个修正的演化定律,该定律考虑了剪切应力变化对断层摩擦的弱化作用,在Dieterich定律的基础上,通过常数c引入了应力速率项:
(9)
c为决定应力速率项弱化作用大小的系数,为一大于零的常数.将公式(6)和(9)结合,本文称之为Nagata定律.显然,当c=0时,Nagata定律退化为Dieterich定律;而当c趋于+∞时,Nagata定律则等效于Ruina定律(Bhattacharya and Rubin,2014).需要强调的是,在目前的研究中,Nagata定律中的摩擦参数a,b和DC的大小依赖于c的取值,其大小与Dieterich定律和Ruina定律的摩擦参数满足如下比例关系:
(1+c)DC|N=DC|DR,
(10a)
(10b)
(a-b)|N=(a-b)|DR,
(10c)
上述三个等式左边的a,b和DC为Nagata定律的摩擦参数,右边的a,b和DC对应Dieterich和Ruina定律.
线性稳定性分析是1D弹簧-滑块模型研究中的一个重要方面.结合Dieterich定律或Ruina定律,对1D弹簧-滑块系统的稳定性分析结果表明,弹簧的临界刚度可以表示为(Ruina,1983;Segall,2010):
(11)

(12)

2 结果
基于Nagata模型,在1D弹簧-滑块模型的近似下,结合公式(1)(5)(6)和(9),采用四阶变步长的Runge-Kutta算法,我们实现了在无扰动、静态扰动、周期性扰动三种情况下,对断层摩擦过程的数值模拟,由此获得不同应力扰动对断层演化进程的影响.为了便于对比模拟结果,本文采用Kato(2001)模型所设定的参数值,如表1所示.这组模型参数和初始条件可以模拟加州圣安德烈亚斯断层大地震的震前滑动的状态.
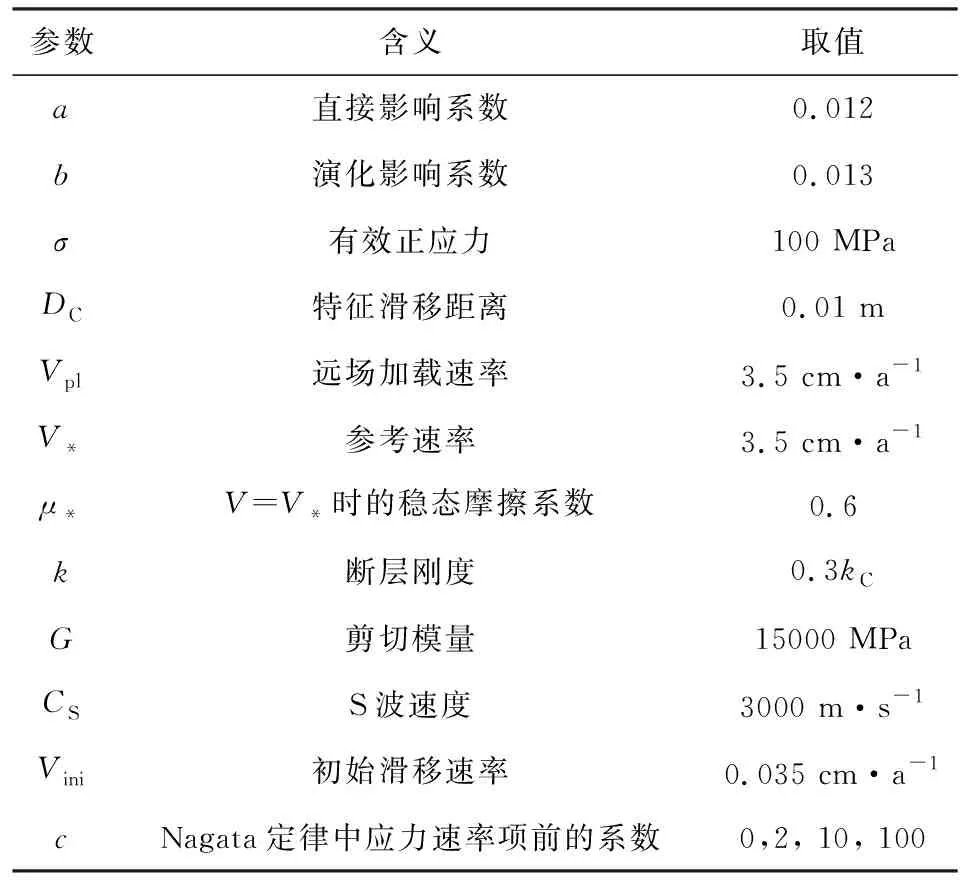
表1 模型参数的含义和取值Table 1 Parameter definitions and values of model
2.1 静态扰动下的断层演化
假定t=0时刻施加应力扰动Δτ0H(t),扰动前系统处于稳定滑移状态,扰动瞬间应力和速率发生突变,扰动后系统以恒定的速率演化至新的稳态.图1展示了不同c值时Nagata模型的应力Δτ随滑动位移的演化过程,这里Δτ指的是扰动后某一时刻应力相对于最终达到新的稳定滑移状态时应力的水平.
由图1可以看出,当c较小时,Nagata模型对正、负两个方向扰动的响应是完全不对称的,对于相同大小的负向扰动,它能在更小的位移上达到稳态水平,这同Dieterich模型给出的结果一致(Kato and Tullis,2001;Bhattacharya and Rubin,2014);当c较大时,Nagata模型对正、负两个方向扰动的响应则趋于对称,如图1c和图1d中c取10和100时所给出的图像,这同Ruina模型给出的结果接近(Kato and Tullis,2001;Bhattacharya and Rubin,2014).实际上,当c=0时,Nagata模型退化为Dieterich模型;而当c趋于+∞时,Nagata模型等价于Ruina模型;随着c由0增大到 +∞,Nagata模型对正、负扰动的响应逐渐由不对称向对称转变.Nagata模型的这一特征,本质上源于其演化方程(9)中引入了应力速率项,图1给出的结果同Bhattacharya和Rubin(2014)的结果一致,也同Dieterich模型和Ruina模型相似(Kato and Tullis,2001).

图1 静态扰动下,Nagata模型的剪切应力随滑动位移的演化不同子图对应了不同c值的Nagata模型的剪切应力演化,(a)(b)(c)和(d)分别对应c = 0,2,10和100;不同颜色的曲线对应不同方向(正向或负向)和大小的静态应力扰动.Fig.1 The evolution of shear stress with slip displacement by Nagata model under a static changeEach subplot shows shear stress evolution of Nagata model with a given c value. (a), (b), (c), and (d) correspond to c=0, 2, 10 and 100, respectively; and curves with different colors correspond to static stress perturbations with different sign (positive or negative) and magnitude.
上述结果也说明我们采用Nagata模型来模拟断层演化的一个重要原因.Dieterich模型和Ruina模型不能同时解释断层摩擦的时间依赖性和速率依赖性:前者可以表达滑移速率为0时的断层愈合过程,但是对正向扰动和负向扰动的响应是不对称的;后者虽然对正、负向扰动的响应是对称的,可它不允许滑移速率为0,即不能表达断层愈合过程.然而,研究表明,Nagata模型则综合了Dieterich模型和Ruina模型的优点,在具有正负扰动响应对称性的同时又可以表达断层的愈合过程.因此,本文选取了Nagata模型来模拟断层演化过程,重点在于探讨应力扰动对断层失稳时间、地震周期等方面的影响.

(13)
公式(13)中H=b/DC-(1+c)k/σ,ta为一特征时间尺度,表示断层成核过程的时间尺度(Dieterich,1994;Beeler and Locker,2003).在静态扰动作用下,断层失稳时间ts则更新为(Kame et al.,2013b):
(14)
从公式(13)和(14)可以看出,在静态应力扰动下,断层失稳时刻与扰动方向和大小有关.对公式(14)进行近似分析,当负向应力扰动Δτ0≪-aσ/(1+c)时,可以简化为:
(15)
从公式(15)可以看出,较大的负向静态扰动下,失稳时刻ts与扰动大小Δτ0近似成正比.而当正向扰动Δτ0≫aσ/(1+c)时,我们可将公式(14)简化为:
(16)

图2 静态扰动下,Nagata模型的滑移速率和位移随时间的演化不同子图对应了不同c值的Nagata模型的滑移速率或位移演化,(a)(b)(c)和(d)分别对应c = 0,2,10和100;不同颜色的曲线对应不同方向(正向或负向)和大小的静态应力扰动.Fig.2 The evolution of slip rate and displacement with time by Nagata model under a static changeEach subplot shows slip rate or displacement evolution of Nagata model with a given c value. (a), (b), (c), and (d) correspond to c=0, 2, 10 and 100, respectively; and curves with different colors correspond to static stress perturbations with different sign (positive or negative) and magnitude.
从公式(16)可以看出,较大的正向静态扰动下,失稳时刻ts与扰动大小Δτ0的指数成正比.实际上,Perfettini等(2003a)也得到了静态应力扰动下失稳时刻的类似结果.
综合上述关于静态应力扰动的研究,可以得到结论:在负向扰动下(Δτ0<0),断层失稳比无扰动情形更推迟发生,且扰动量越大则推后量越大,失稳时刻ts与扰动大小Δτ0成正比;在正向扰动下(Δτ0>0),断层失稳比无扰动情形更提早发生,失稳时刻ts与扰动大小Δτ0的指数成正比.总之,负向应力扰动在一定程度上能减缓断层演化进程,而正向应力扰动则能促进断层失稳.
2.2 周期性扰动下的断层演化
在本文中,周期性应力扰动函数f(t)=Δτ0sin(ωt),因此扰动量的变化由幅值Δτ0和角频率ω所决定,而ω与扰动周期Tr相关(Tr=2π/ω).考虑到季节性气候(例如河流或湖水上涨)造成的应力变化周期约为一年,那么不妨取Tr=1 a,则Nagata模型在不同幅值的周期性扰动下,速率和位移随时间的演化过程如图3所示.其中,扰动幅值Δτ0分别取0.1 MPa,0.5 MPa,1 MPa,2 MPa.
由图3可以看出,与无扰动情形(Δτ0=0)相比,周期性应力扰动下的断层失稳总是提前发生,且扰动幅值越大,失稳时间提前量越大.造成此现象的原因,可以从累积滑动位移角度得到了解.从图3可以看出,虽然滑移速率随时间的增加存在一定波动(a1,b1,c1,d1),但是累积滑动位移随时间的增加是单调递增的(a2,b2,c2,d2).当应力扰动量大于0时,滑移速率相应增大,累积滑动位移增加量也较大;而当应力扰动量小于0时,滑移速率是下降的,从而使得累积滑动位移增加量上升变缓.事实上,扰动加载的持续时间为Tc,累积滑动位移量约为Δu≈V0Tc·I0(X),I0(X)为零阶修正的Bessel函数(I0(X)≥1,X=(1+c)Δτ0/(aσ)).因此,sin(ωt)形式下的周期性扰动促进了断层滑移,故失稳时间总是提前.
除了季节性气候变化的因素,自然界还存在更多种频率的应力扰动,例如地震应力波和人类活动的干扰(地热开采,油页岩开采等).为此,我们进一步探讨了扰动频率对断层演化进程的影响.图4展示了Nagata模型在不同频率的周期性扰动下,速率和位移随时间的演化过程.其中,固定扰动幅值Δτ0=1 MPa,调整扰动周期Tr=0.5 a,1 a,2 a.观察图像可以看出,对于相同的扰动幅值,不同扰动频率下,断层在相近的时刻发生失稳.这一现象说明,周期性扰动下的断层失稳时刻主要受扰动幅值影响,而扰动频率对失稳时间的影响很小.
图4中的现象和结论也可以从近似解析解的角度进行分析和解释.类似于Perfettini等(2003b)和Ader等(2014)得到的结果,当扰动周期Tr≪ta时,断层的失稳时间td可近似为(详见后文附录A):
(17)
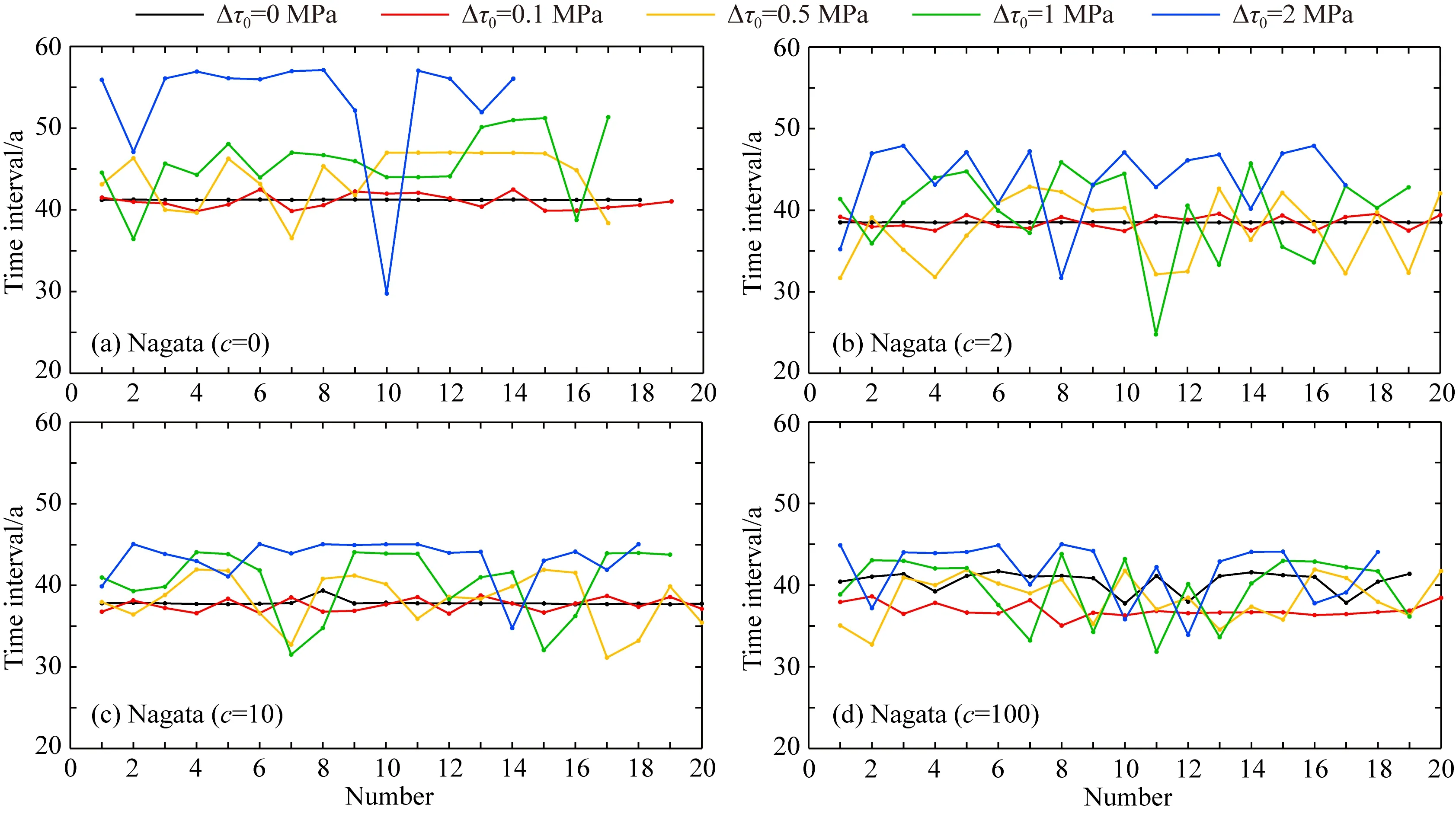
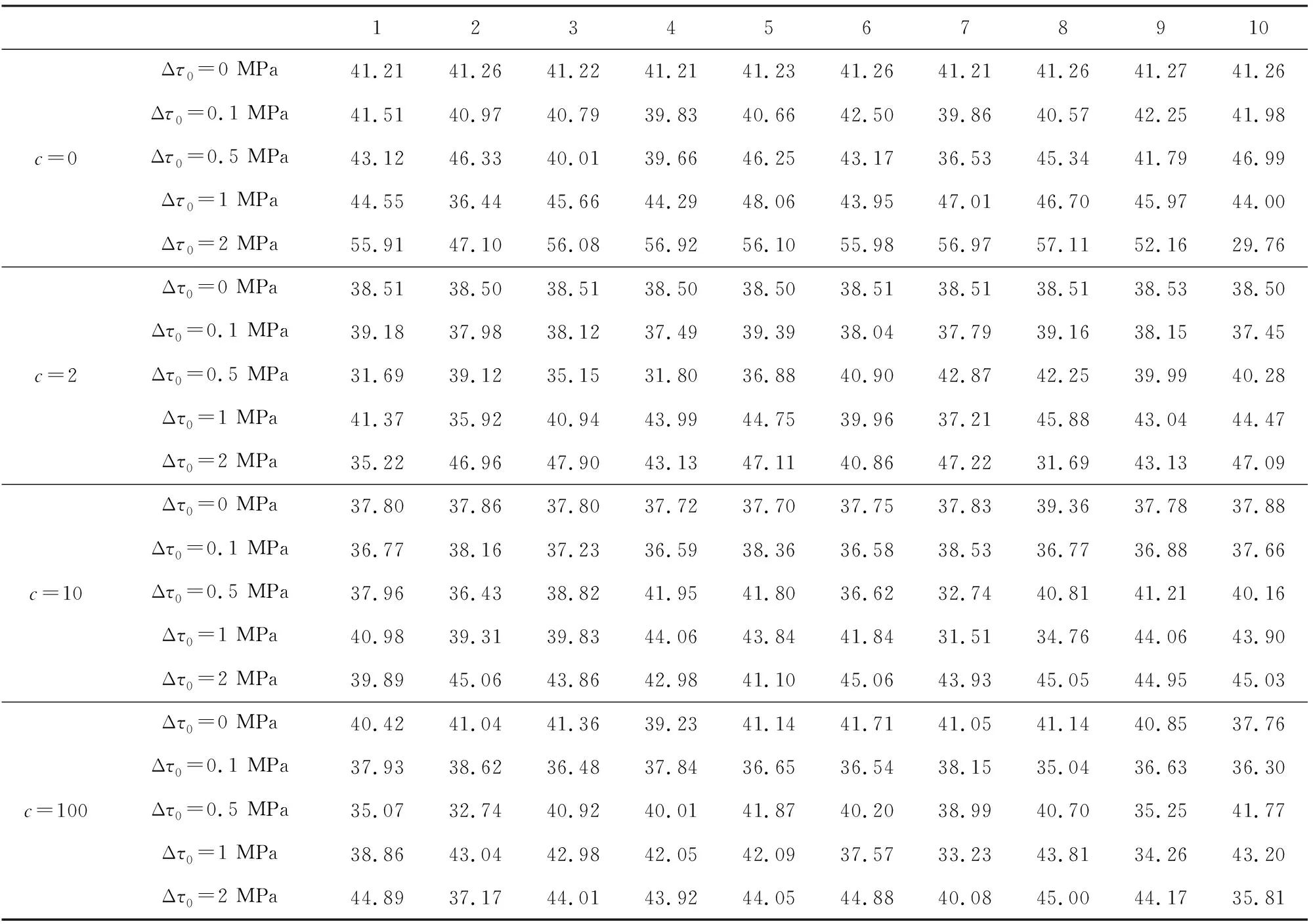
当X>0时,I0(X)>1.对比公式(13)和(17)可以看出,无论Δτ0取值如何,总有td 图4 不同频率的周期性扰动下,Nagata模型的滑移速率和位移随时间的演化不同子图对应了不同c值的Nagata模型的滑移速率或位移演化,(a)(b)(c)和(d)分别对应c=0,2,10和100;不同颜色的曲线对应不同频率的周期性应力扰动.Fig.4 The evolution of slip rate and displacement with time by Nagata model under different periodic disturbance frequencyEach subplot shows slip rate or displacement evolution of Nagata model with a given c value. (a), (b), (c), and (d) correspond to c=0, 2, 10 and 100, respectively; and curves with different colors correspond to periodic stress perturbations with different frequency. 综合上述关于周期性应力扰动的研究,可以得到结论:对于简谐函数所描述的周期性应力扰动,无论扰动量的大小、频率和持续时间如何,周期性触发下的断层失稳总是提前发生,且扰动幅值越大,则失稳提前量越大.进一步讲,如果地震应力波都可以由傅里叶级函数表达,那么地震造成的周期性应力扰动总是能导致断层失稳时间的提前,且提前量与该地震的震级有关. 前面两部分研究的都是断层的单次失稳,若加入辐射衰减项,即公式(1)右边的最后一项,我们可以实现断层在时间域上演化的多次循环解,从而了解周期性应力扰动对地震复发周期的影响.例如,采用应力扰动函数f(t)= Δτ0sin(2πt/Tr),其中,Δτ0=1 MPa,扰动周期Tr=1 a,可得如图5、图6和表2所示的模拟结果.图5给出了演化过程中的断层滑移速率和累积滑动位移,图6和表2则分别给出了前21次和前11次失稳中,每相邻两次失稳之间的时间间隔,图6横坐标和表2第一行的数字表示失稳间隔的序号.从图5可以看出,当c值较小时(c=0,2),无应力扰动加入(红色曲线)的断层演化呈现出确定的周期性,如c=0时的循环周期约为41.2 a,c=2时的循环周期为38.5 a(图6和表2).当c≫1时,断层循环的重复发生时间间隔会出现极小的波动,但仍然保持了固有的周期性,如c=10时的循环周期约为37.8 a,c=100时的循环周期约为40.5 a(图6和表2).图5中黑色实线则分别给出了Δτ0=1 MPa时Nagata模型多次循环下的滑移速率和滑动位移的变化.从滑移速率随时间变化的特征来看,应力扰动主要影响断层震间阶段的演化,会出现高频波动的现象,波动周期与扰动周期Tr一致,均远小于震间阶段的持续时间.显然,从图5、图6和表2可以看出,断层失稳的时间间隔出现了大于或小于固有周期(无应力扰动情形的周期)的现象,断层演化不再具有明确的周期性.当扰动量Δτ0增加时,断层失稳的时间间隔会变得更不规则,而这种不规则性在c=0时较为明显. 图5 周期性扰动下,Nagata模型的滑移速率和位移关于时间的周期解不同子图对应了不同c值的Nagata模型的滑移速率或位移演化,(a)(b)(c)和(d)分别对应c=0,2,10和100;黑色曲线为周期性扰动情形,红色曲线为无扰动情形.Fig.5 Periodic solutions of slip rate and displacement with time by Nagata model under periodic disturbanceEach subplot shows slip rate or displacement evolution of Nagata model with a given c value. (a), (b), (c), and (d) correspond to c=0, 2, 10 and 100, respectively; and the black curve corresponds to the periodic disturbance case, and the red curve corresponds to the undisturbed case. 图6 周期性动态扰动下,Nagata模型的失稳时间间隔不同子图对应了不同c值的Nagata模型的失稳时间间隔,(a)(b)(c)和(d)分别对应c=0,2,10和100;不同颜色的曲线对应不同幅值的周期性应力扰动.Fig.6 Instability time interval of Nagata model under periodic dynamic disturbanceEach subplot shows instability time interval of Nagata model with a given c value. (a), (b), (c), and (d) correspond to c=0, 2, 10 and 100, respectively; and curves with different colors correspond to periodic stress perturbations with different magnitude. 表2 无扰动和周期性扰动情形下,Nagata模型的失稳时间间隔对比(单位:a)Table 2 Comparison of instability time intervals by Nagata model in the case of no disturbance and periodic disturbance (unit: a) 本文通过数值方法,实现了静态和周期性应力扰动下,不同c值条件下Nagata模型对断层演化过程的模拟.研究表明,正向静态扰动和所有周期性扰动都可以使失稳时间提前(图2,图3),但是相同Δτ0条件下,两种扰动造成的时间提前量不同.当Δτ0分别取0.1 MPa,0.5 MPa,1 MPa,2 MPa时,与无扰动(Δτ0=0 MPa)相比,Nagata模型在静态扰动和周期性扰动下的失稳时刻如表3所示(结果保留小数点后两位). 表3数据显示,对于相同的Δτ0,与周期性扰动相比,静态扰动下的断层失稳更早、时间提前量更大.这也揭示了周期性扰动和静态扰动的不同之处.公式(14)和(17)可以从模型原理角度解释对于相同Δτ0,静态扰动比周期性扰动下的断层失稳更早发生的原因.虽然周期性扰动下的时间提前量小于静态扰动的结果,但周期性扰动对失稳时刻的影响还是十分明显,尤其当Δτ0很大时. 表3 静态和周期性扰动下,Nagata模型的失稳时刻(单位:a)Table 3 Instability time by Nagata model in the case of static and periodic disturbance (unit: a) 另外,从表3还可以发现,在相同的扰动条件下,c值越大,断层失稳所需时间越短.实际上,当c=0时,Nagata模型的失稳时刻最晚,同Dieterich模型一致;随着c的增大,Nagata模型失稳越来越早;当c趋于+∞时,Nagata模型的失稳时刻最早,接近于Ruina模型. 采用Nagata模型实现本文给出的数值模拟结果,其模型参数的取值也十分重要.对于目前的研究,Nagata模型的摩擦参数a,b和DC的取值与c值大小有关,在给定a,b和DC原始值的基础上,按照公式(10)给出的比例关系取值.公式(10)并非随意得到的,而是通过严格的物理与数学推导所得到(Bhattacharya and Rubin,2014),但由于文章的篇幅有限,在此不再展开讨论. 即使Nagata模型能兼顾Dieterich模型和Ruina模型的优点,同时解决扰动响应对称性的问题和断层愈合过程的问题,但是常参数c的取值仍然是一个尚未解决的问题.虽然应力速率项的引入使Nagata模型在c较小时具有Dieterich模型的特征,在c较大时具有Ruina模型的特征,但是也很难找到一个合适的c值,将两种模型的特征同时融合在某一个Nagata模型中.若c值过小,则Nagata模型对正、负向扰动的响应不对称;若c值过大,则按公式(10)给出的摩擦参数不在合理范围内.前人最常用的c值为2,也有人认为c的上限为10(Bhattacharya et al., 2015),但目前没人能给出c的最佳值. 本文从Nagata定律出发,结合1D弹簧-滑块模型,通过四阶变步长的Runge-Kutta算法,实现了对静态和周期性应力扰动下断层演化过程的数值模拟.研究的重点集中在Nagata模型在不同扰动下的失稳时刻和地震周期,探讨应力扰动对断层失稳机制的影响.主要发现和结论如下: (1)当c=0时,Nagata模型退化为Dieterich模型,对正负静态扰动的响应是不对称的;当c趋于+∞时,Nagata模型等价于Ruina模型,对正负静态扰动的响应是对称的;随着c的增大,Nagata模型下的静态应力扰动响应由不对称逐渐趋于对称. (2)在静态扰动下,断层失稳时刻与扰动的方向和大小有关:与无扰动情形相比,对于负向扰动,失稳总是推迟发生,且时间推后量与扰动量大小成正比;对于正向扰动,失稳总是提早发生,且时间提前量与扰动量的指数成正比. (3)简谐应力扰动总是使断层失稳提早发生,且扰动振幅越大,失稳提前量越大;但是,扰动频率或扰动周期对失稳时刻并无显著影响.对于相同的Δτ0,正向静态扰动下的断层失稳更早,时间提前量比周期性扰动时的更大. (4)当远场加载速率给定且为常量时,若无应力扰动,则断层的失稳时间间隔基本相同,断层演化过程显示出确定的周期性;但在周期性应力的扰动下(简谐应力变化),断层失稳时间间隔则会出现明显的非周期性,从而使得断层在时间域上的演化变得更为复杂. 附录A 不同扰动下的断层失稳时刻 在断层演化过程中,摩擦剪应力τf始终等于加载剪应力τd,结合正文原理部分的公式(1)(5)(6),关于时间求导,整理可得: (A1) 其中,H=b/DC-(1+c)k/σ.公式(A1)两边同时做不定积分,并用初始条件确定积分常数,经过一系列整理和简化可得: (A2) 对于不同的情形,τload的具体形式不同,下面就分别从无扰动、静态扰动、周期性扰动三种情形下出发,分析推导断层失稳时间tf、ts、td. 无扰动情形 对于无扰动情形,外界加载应力τload可由正文的公式(2)表达,将其代入公式(A2),积分后整理可得: (A3) tf就是无扰动情形下的断层失稳时间. 静态扰动情形 对于静态扰动情形,外界加载应力τload可由正文的公式(3)表达,将其代入公式(A2),积分后整理可得: (A4) ts就是静态扰动情形下的断层失稳时间. 周期性扰动情形 对于周期性扰动情形,外界加载应力τload可由正文的公式(4)表达,将其代入公式(A2): (A5) 以2π/ω为间隔,将积分总区间[0,td]划分为n个子区间(n=ωtd/2π),若扰动频率足够大,满足ω≫2π/td,则公式(A5)可以简记为: (A6) (A7) g(Δτ0)表示公式(A5)第二部分周期函数在一个周期上的积分值: (A8) 令Y=ωy,利用换元法,再利用正余弦函数的周期性和对称性,可将公式(A8)改写为: (A9) (A10) td就是周期性扰动情形下的断层失稳时间.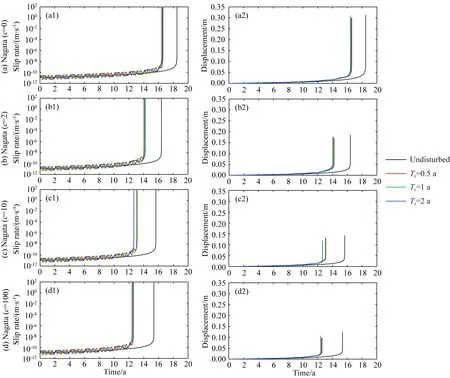
2.3 周期性扰动对地震复发周期的影响

3 讨论

4 结论