基于深度学习的内磁层等离子体密度动态演化模型
2022-06-02郭英杰倪彬彬付松胡泽骏郭建广冯明航周若贤郭德宇闫玲马新顾旭东
郭英杰, 倪彬彬,2*, 付松, 胡泽骏, 郭建广, 冯明航,周若贤, 郭德宇, 闫玲, 马新, 顾旭东
1 武汉大学电子信息学院空间物理系, 武汉 430072 2 中国科学院比较行星学卓越创新中心, 合肥 230026 3 中国极地研究中心国家海洋局极地科学重点实验室, 上海 200136 4 中国气象局国家空间天气监测预警中心, 北京 100081
0 引言
等离子体密度作为研究空间环境中带电粒子时空演化的重要参量,对于理解磁层中的物理过程有着重要意义,其动态演化过程更是对预报和防范灾害性空间天气有着潜在价值.地球空间环境中的冷等离子体(~1 eV)是空间带电粒子中的主要成分,构成这些冷等离子体的带电粒子被地球磁场和共转电场共同束缚,形成了被称为等离子体层的气泡状区域(Lemaire and Gringauz, 1998).等离子体层作为空间中等离子体密度相对稠密的区域,其密度典型值通常在10~104cm-3,空间分布在2~7RE(RE为地球半径)之间并随着地磁活动而变化.通常认为等离子体层的动态变化由日侧对流和同地球共转两种机制所控制(Darrouzet et al., 2009):在磁平静期,共转机制占主导地位,等离子体层由来自电离层顶部的离子上行填充至4~7RE(Goldstein et al., 2003);在磁暴期间,日侧对流占主导地位并侵蚀等离子体层,等离子体层顶可被压缩到低于2RE.通常我们可以通过等离子体密度来确定等离子体层形状(Guo et al., 2021;Moldwin et al., 2002).除此之外,等离子体密度常作为空间环境中模型的输入,能够帮助我们更好地理解内磁层中的波粒相互作用(Fu et al., 2016, 2018, 2019, 2020;Fu and Ge, 2021;Huang et al., 2018; Ma et al., 2020; Ni et al., 2016, 2018, 2019, 2022a, 2022b;Wang et al., 2020;Xiang et al., 2021;Zhou et al., 2020;顾旭东等,2020;朱佳楠等,2021).因此,对等离子体密度的时空演化进行有效的预测,对于我们理解空间环境中物理过程和发展空间天气的预报技术都非常重要.
多年以来,科学家都在对预测等离子体密度的动态变化不断开展研究工作,并已经开发了许多经验模型来统计描述内磁层中的等离子体密度(Carpenter and Anderson,1992; Ozhogin et al., 2012; Sheeley et al., 2001).这些模型以卫星观测数据为基础,利用卫星观测数据进行拟合,并得到确定的数学表达式.尽管这些经验模型在过去被大量使用,但是它们仍然有一定的局限性,例如无法在连续时间内(如磁暴事件)对全局分布的等离子体密度演化进行重构,因此无法预测等离子体密度随时空的动态变化等.基于此类问题,一种新的数据驱动建模技术即神经网络模型逐渐被广泛应用于空间天气预报(Bala et al., 2009;Bortnik et al., 2016;Costello, 1998;Elman,1990;Guo et al.,2021;Kugblenu et al., 1999;Lethy et al., 2018;Tan et al., 2018).在预测等离子体密度动态演化方面,Chu 等(2017a)使用了THEMIS(Time History of Events and Macroscale Interactions during Substorms)卫星2008—2012年由飞船电势推导得来的等离子密度观测数据,采用了双隐藏层结构的前馈神经网络对等离子体密度建模;Chu 等(2017b)使用了ISEE(International Sun-Earth)、CRRES(The Combined Release and Radiation Effects Satellite)、Polar和IMAGE(Imager for Magnetopause-to-Aurora Global Exploration)等四颗卫星的等离子体密度观测数据,采用了与Chu 等(2017a)相似的双隐藏层结构的前馈神经网络,建立了三维等离子体密度演化模型(DEN3D);Zhelavskaya等(2017)使用了范阿伦(Van Allen Probe)卫星上的等离子体密度观测数据,采用了单隐藏层结构的前馈神经网络对等离子体密度进行建模.基于以上工作的经验和优点,在本工作中,(1) 我们使用了包含五隐藏层的深度神经网络架构,该架构具备更强的数据特征捕捉能力,从而对范阿伦卫星上的等离子体密度观测数据进行拟合建模.(2) 本模型重点关注2~7L地球空间范围内的等离子体密度时空动态演化过程,有利于进一步深化使用范阿伦卫星数据和分析潜在的重要物理机制.(3) 对于等离子体密度数据集的时间序列数据集建模,之前的工作往往直接随机划分训练集、验证集和测试集,可能会造成数据泄漏,从而高估模型性能.为了避免数据泄露,本模型采用了与Guo等(2022)中相似的数据集处理方式,对于数据集分块后再进行随机划分,从而保证了三个数据集之间的独立性.
在本研究中,我们使用范阿伦卫星的等离子体密度观测数据建立了一个稳定的深度神经网络模型,用于预测内磁层中等离子体密度的动态演化过程.通过对比数据集外的磁暴事件中模型的输出与范阿伦卫星的实际观测值,我们进一步验证了该模型在磁暴事件中的预测效果.此外,我们将模型进一步应用于2012年4月24日的磁暴事件中,成功重构了不同地磁条件下赤道面等离子体密度的全球演化过程,包括等离子体层压缩和恢复,以及等离子体层羽流的形成和消失等密度演化现象.本文的结构如下:第1节介绍了本研究所采用的卫星观测数据和深度学习建模方法,第2节针对具体磁暴事件中的等离子密度变化进行了模拟、重构和比较分析,第3节对深度学习的建模结果进行了总结和讨论.
1 数据与模型方法
1.1 卫星观测数据
本文使用范阿伦卫星2012年10月1日至2015年12月31日期间的观测数据作为数据集,训练得到稳定的深度神经网络模型.我们使用了范阿伦A、B两颗运行轨道和携带仪器相同的卫星,近地点约1.1RE, 远地点约5.8RE.本研究使用到的电子密度数据由范阿伦卫星搭载的电磁场综合科学仪器套件(Kurth et al., 2015)(Electric and Magnetic Field Instrument Suite and Integrated Science, EMFISIS)得到,它能提供频率范围10 Hz~400 kHz高精度的波动观测数据,我们可以通过其提供的上混杂波频率得到电子密度信息:
(1)
其中电子等离子体频率fpe和电子回旋频率fce由下式得到:
(2)
其中B是磁场强度,ne是电子密度,qe是电子电荷,ε0是真空介电常数,me是电子静止质量.在本研究中我们使用EMFISIS提供的L4数据产品,并对所有数据进行了5 min平均,数据集总共包含396285个数据点(51.9% 来自a星,48.1% 来自b星).图1展示了电子密度数据集在(L-shell, MLT)上的空间分布.

图1 电子密度数据集在 (L-shell, MLT) 上的空间分布图Fig.1 The data-point distribution of electron density as a function of L and MLT
本模型旨在预测不同地磁活动条件下内磁层中等离子体密度的动态变化.模型的输入包括位置信息(L-shell, MLT)和地磁指数SYM-H(环电流强度)、AL(西向电集流)和太阳风参数F10.7指数(太阳射电通量).其中,(1)SYM-H指数主要描述环电流强度.磁暴期间由于离子的注入,环电流强度随之增强,离子向西漂移形成的电流会在地球表面产生南向磁场,从而减小地球表面磁场的水平分量,同时也对共转电场造成影响,进而影响等离子体层的变化.(2)AL指数描述西向电集流引起的最大磁场扰动,能很好地衡量亚暴的活动强度.同时,AL指数和修正后的太阳风电场高度相关(McPherron et al., 2015),影响着地球空间中对流电场的大小,进而影响等离子体密度的空间分布.(3)F10.7指数衡量10.7 cm射电辐射通量,表征太阳的活跃程度.本文所使用的太阳风参数F10.7指数,地磁指数AL, SYM-H的数据均来自于OMNI Web.由于等离子体密度的变化与其历史状态密切相关,因此对于每个卫星观测点,模型的输入包含了前3天的SYM-H指数,前5小时的AL指数,以及前3天的F10.7指数,详见表1.

表1 神经网络模型的输入参数Table 1 Summary of the model input
1.2 深度神经网络模型
深度神经网络(Deep Neural Network, DNN)是由前馈神经网络(Feedforward Neural Network, FNN)发展而来的,用于解决一些更复杂的非线性问题.深度神经网络保留了前馈神经网络非线性拟合的能力,同时增强了网络学习能力和网络容量.但是更多的神经元和更深的网络结构意味着更容易过拟合,因此选择合适的网络结构对于模型性能非常重要.在本文2.1节中,我们对比了不同隐藏层神经网络结构的预测效果,并选择使用了一个相对深而窄的神经网络模型结构.如图2所示,本模型由一个输入层,一个输出层以及五个隐藏层构成,五个隐藏层分别包含100、60、40、20、10个神经元.其中,单个神经元的输出可由下式得到:
(3)

Sigmoid:f(zj)=1/(1+e-zj),
(4)
ReLU:f(zj)=max(0,zj),
(5)

图2 深度神经网络模型示意图Fig.2 Schematic diagram of deep neural network model
同时我们加入了Dropout层,通过随机地从网络中移除神经元防止过拟合现象的发生(Srivastava et al., 2014).
为了更好地评估、改善神经网络模型的性能,我们按照70%、15%和15%的比例将数据集划分为训练集、验证集和测试集.针对类似本工作中等离子体密度数据集的时间序列数据集,直接随机划分训练集、验证集和测试集可能会造成数据泄漏,从而高估模型性能.为保证三个数据集之间的独立性,本工作采用了与Guo等(2022)中相似的处理方式,对于数据集分块后再进行随机划分.本神经网络模型使用训练集数据进行训练,通过验证集数据调整模型的超参数设定,并利用测试集数据评估最终模型性能.此外,在第2节中,我们对数据集外的磁暴事件进行了模拟和比较,进一步验证了模型的实际预测效果.
图3展示了训练集、验证集和测试集以及全数据集上观测值的和模拟的等离子体密度之间的相关性.黑线是最小二乘法拟合得到的,表示着观测值和模型值完全一致.每个子图的左上角展示了基于log10(ne)计算而得的均方根误差(Root Mean Square, RMSE)和线性相关系数.模型在训练集、验证集和测试集的相关系数分别为0.9296,0.9289和0.9307,均方根误差分别为0.3054,0.3066和0.3026,可以认为此模型在三个数据集上的表现是一致的,过拟合现象并没有出现(即测试集的表现明显差于训练集和验证集),表明了该模型对三个数据集都拟合良好且具备一定的泛化能力.在测试集上的表现进一步说明该模型在数据集外具有良好的预测能力,为我们接下来开展内磁层波粒相互作用的相关工作提供了坚实基础.
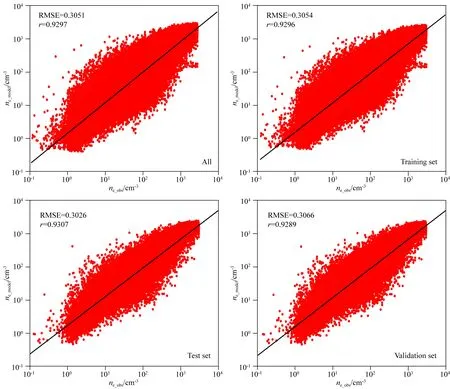
图3 四个数据集(全部、训练、测试和验证)的深度神经网络模型预测值与局地等离子体密度观测值之间的相关性分析.图中直线通过最小二乘法拟合得到,每幅子图的左上角为模拟值与观测值之间的相关系数(r)和均方根误差(RMSE)Fig.3 Correlation between the observed in situ plasma density and predicted values by the deep neural network model for four data sets (all, training, test, and validation). The straight line is fitted by least squares, the correlation coefcients (r) and RMSE are shown in the top left corners
2 结果分析
2.1 数据集外模型预报结果
本节,我们使用三个不同结构的神经网络模型对数据集外的磁暴事件中等离子体密度的动态演化进行模拟,并与范阿伦卫星的实际观测值进行了比较.图4展示了范阿伦A星于2016年3月5日至9日的等离子体密度观测数据和三个不同结构的神经网络模型的输出值的对比结果.图4a展示了地磁指数SYM-H和0.1倍AL的绝对值的变化,描述了这段时间的地磁活动情况,图4b—d对比了范阿伦a星的等离子体密度观测数据(蓝线)与三个具有不同神经网络结构的模型输出结果(红线)的差别,模型的预测结果(红线)和观测值(蓝线)在时间轴上是一一对应的:图4b中的神经网络模型包含两个隐藏层,分别含有60和10个神经元;图4c中的神经网络模型为我们在第2.2节中介绍并最终采纳的模型;图4d中的神经网络模型较为复杂,包含10个隐藏层,分别有300、260、240、220、180、160、140、120、60和10个神经元.

图4 范阿伦A星等离子体密度观测值(蓝色)与(b)3隐藏层,(c)5隐藏层,(d)10隐藏层神经网络模型输出值(红色)的比较.顶部子图(a)展示了同时段SYM-H指数(红色)和AL指数的绝对值(蓝色)Fig.4 Comparison between the observed electron density (blue) obtained from VAP-A and the (b) 3-hidden-layer, (c) 5-hidden-layer, (d) 10-hidden-layer neural network model outputs (red). The top panel (a) shows the SYM-H index (red) and the absolute values of the AL index (blue)
如图4a所示,磁暴的初相始于2016年3月6日,SYM-H指数突然增加,随后迅速下降至小于-100 nT,标志着一次强磁暴事件的发生.图4b—4d表明了我们的模型对于数据集外的磁暴事件有一定的预报能力.同时,不同模型结构之间的表现也有细微的差别:图4b中展示的两隐藏层神经网络结构相对简单,对于磁暴事件中的等离子体密度扰动变化的预测与实际情况相差较大;图4d中展示的具有10个隐藏层结构的神经网络模型在低密度区域表现不佳,潜在原因是模型过于复杂所导致的过拟合现象,即模型过于紧密地匹配训练集,以至于在数据集外的事件中表现不佳;图4c中展示的具有5个隐藏层结构的神经网络模型表现最好,因此该模型结构被视为内磁层等离子体密度动态演化模型的最佳模型结构.
2.2 2012年4月24日磁暴事件的全球等离子体密度重构
基于上节深度神经网络模型在磁暴期间的良好表现,我们在本节中使用深度神经网络模型对于2012年4月24日磁暴事件期间等离子体密度的全球演化进行了重构,并选取了9个具有代表性的时间点进行展示.
与图4a相似,图5顶部的子图展示了2012年4月21日至28日的地磁活动情况,红线表示SYM-H指数,蓝线表示0.1倍AL指数的绝对值.磁暴的初相开始于4月23日,随后SYM-H指数迅速下降,标志着磁暴进入了主相阶段.SYM-H指数的最小值于4月24日达到-135 nT,随后进入恢复相,逐渐恢复完全平静状态.我们分别选取了磁暴发生前较为平静的一段时间(a,b,c)、磁暴发生的初相(d)、主相(e,f)和恢复相(g,h)共9个时间点对于等离子体密度的全球分布进行了重构.
图5a—5i展示了深度神经网络模型对于赤道面L-shell=2~7的区域中等离子体密度分布的重构,每个子图对应的时间点在图5顶部子图中用竖直虚线标出,子图中的颜色所对应的等离子体密度在图5右侧标出,等离子体层的边界(这里我们近似地认定100 cm-3区域为等离子体层顶)用黑色虚线标出.在磁暴开始前相对平静期间,如图5a—5c所示,等离子体层相对稳定,等离子体层边界在L-shell=4~5的区间.磁暴进入主要阶段后,如图5e所示,等离子体层在黄昏侧表现出的突起是由于向日侧的磁层顶重联(Dayside Magnetopause Reconnection, DMR)导致的(Chappell et al., 1970;Lemaire and Gringauz, 1998).在地磁活动增强时,DMR驱动的对流增强可能造成等离子体的方位角运动,使得等离子体层外层剥离,即等离子体层侵蚀(Erosion).等离子体层的这一凸起结构也被称为等离子体层羽流(Plasmaspheric Plume)(Darrouzet et al., 2006, 2008;Zhang et al., 2019).随着磁暴进入恢复相,如图5f—5i所示,羽流消失,等离子体层逐渐恢复,层顶位置也随之移动至L-shell=4~5的区间.深度神经网络模型为我们提供了不同地磁活动期间全球等离子体密度变化的完整模拟,而磁暴中等离子体层的变化特征可以结合经验公式作为边界条件作进一步研究.

图5 (A) 2012年4月24日磁暴事件中SYM-H指数(红色)和AL指数(蓝色)的绝对值; (B) 深度神经网络模型对磁暴期间特定时刻等离子体密度的全球分布的重构,(a)—(i) 中虚线表示等离子体层顶位置,每幅子图对应时刻在(A)中用黑色虚线中标出.Fig.5 (A) The SYM-H index (red) and the absolute values of the AL index (blue) during the April 24, 2012 storm event. (B) The reconstructed global distribution of plasma density at specific moments during the storm event based on the DNN model. The dotted lines in (a)—(i) represent the position of plasmapause. The corresponding time is indicated by black dotted lines in (A).
3 总结
利用范阿伦双星3年多的高质量等离子体密度观测数据,本文基于机器学习算法训练得到了一个稳定的深度神经网络模型来预测内磁层中的等离子体密度的动态演化.该模型包含5个隐藏层,激活函数包括Sigmoid和ReLU函数,同时以太阳风参数、地磁指数以及卫星对应的位置信息作为输入,考虑了时间、空间、地磁活动情况和历史累积效应对于等离子体密度动态变化的影响,对于研究内磁层动力学过程和预报、防范灾害性空间天气具有重要价值.
本文的主要结论如下:
(1)利用范阿伦双星2012年10月1日至2015年12月31日期间的等离子体密度观测数据训练得到了一个深度神经网络模型.该模型性能在训练集、验证集和测试集上均表现相近且良好,输出结果与观测值的线性相关系数约为 0.93,均方根误差约为 0.3.
(2)通过与2016年3月5日磁暴事件中范阿伦卫星等离子体密度观测数据的比较,验证了具有5个隐藏层的深度神经网络模型为最优结构,并进一步证实该模型针对数据集外的事件同样具有良好的预测效果.
(3)通过利用该模型对2012年4月24日磁暴事件中等离子体密度的全球动态变化进行模拟,成功重构了磁暴期间内磁层等离子体密度的全球变化过程,包括等离子体层的侵蚀和恢复,以及羽流的形成和消失,为该模型用于内磁层物理研究创造了条件.
致谢感谢范阿伦卫星团队提供数据,范阿伦卫星等离子体密度数据来源于(http:∥emfisis.physics.uiowa.edu/data/index),地磁活动指数和太阳风参数来源于NASA OMNIWEB(http:∥omniweb.gsfc.nasa.gov).
