计及电网随机性的无功优化控制方法研究*

王建平

(国网山西省电力公司忻州供电公司，山西 忻州 034000)

电力系统的电压无功优化控制为混合非线性控制，表现出多目标、多约束等基本特性[1－3]。目前，关于无功优化控制策略的研究主要是在无功优化控制的算法以及控制目标等方面，因此，怎样有效、确切地描述并解决各种影响电网稳定性的不确定因素，是对电网进行优化控制的重要基础[4－5]。

目前，研究学者在无功优化计算方面做了许多研究工作。文献[6]基于扩展松弛内点法，提出了一种实用型的无功优化计算方法，能够在不增大计算量的前提下，自动辨识并滤除造成优化不可行的约束条件，算例应用结果充分证明了该方法在恢复最优潮流的可行性；文献[7]基于面向对象和模块化的设计思想，开发设计了一款跨平台的无功优化控制软件，该软件兼具数据、网络拓扑架构分析以及无功潮流优化计算等各项功能；文献[8－9]以网损量最小和经济性最高为控制目标，基于改进量子粒子群算法(Quantum behaved Particle Swarm Optimization，QPSO)，提出了一种电力系统无功功率优化控制方法，并通过算例仿真验证了所提算法的有效性；文献[10]考虑风电的接入建立了基于场景分析的多目标无功优化模型，采用最大化模糊满意度指标法将降低电能损失和减小电压偏差量的多目标问题转换为单目标优化问题，不同场景下的算例应用结果证明了所提算法在改善电压质量和降损节能方面的有效性；文献[11]考虑连续和离散变量的基本特性，提出了一种非线性的无功优化控制方法，以降低网损量和减小电压越限值为控制目标，案例应用结果充分证明了该方法的有效性；文献[12]充分考虑无功补偿设备投切次数的限制，建立了分阶段的无功功率动态优化模型，将动态无功优化问题转化为多个时间层面的连续无功优化计算，仿真结果充分证明了该方法的工程应用价值；文献[13]基于遗传网络算法对配电网进行无功优化计算，建立了风力发电机出力模型，计算得到系统各电气参量的期望与标准差，算例应用结果充分证实了其在优化配网无功分布、提升系统稳定性的重要作用。

上述研究文献以电力系统网损值最低为优化控制目标来求得无功潮流的最优结果。可在实际运行状态下，由于电力系统自身的动态、静态稳定特性，最优潮流值会随着负荷的变化而变化，计算值与实际值存在偏差。为此，本文充分考虑实际运行过程的动态变化随机性，首先对初始断面的不确定性场景进行选取，计算常见工况出现的概率；接着，考虑网损值以及电压调整偏差量二者的权重，搭建了多目标的无功功率优化控制模型；最后，基于改进量子粒子群算法对模型进行求解计算，并对算法的基本特性和有效性进行验证。

1 潮流计算基本模型

假设线性分段发电机组的费用函数c(x)如下式所示:

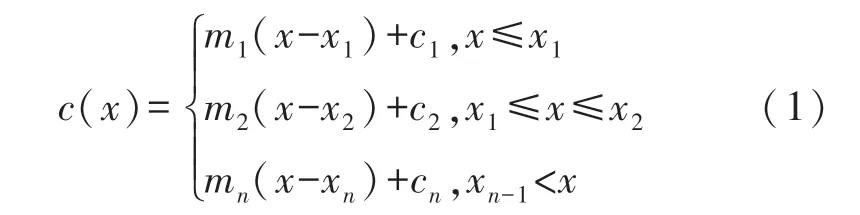
引入变量y，则有:

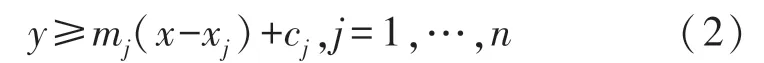
式中:mj为分段线性的斜率，xj为分段线性的分段点，cj为xj对应的纵坐标，如图1 所示。

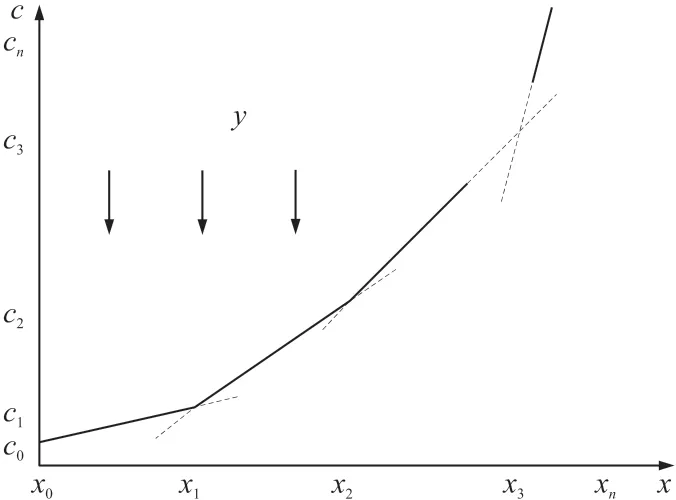
图1 发电机组费用约束函数曲线

对于可调度负荷模型，通常将其当做一台有功出力为负的机组。

对于交直流混合电网，直流输电线一般等价成两台机组，该机组的上下限值受控，且其所传输的功率值也受线性约束:

式中:pt为线路的输出功率；pf为线路的输入功率ploss为有功损耗量。

2 考虑随机因素的无功优化计算系统模型

2.1 初始断面的不确定性场景选取

以0.5 min～1 min 为间隔进行状态估计，由于电力系统存在波动，导致无功电压存在一定的随机偏离。因此，本文利用概率密度函数与随机变量的设置对负荷功率与电压无功的模糊性做出处理[14－15]。

首先，建立负荷不确定性模型，如式(4)所示:

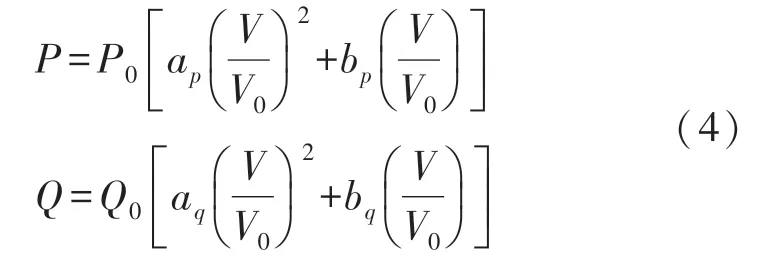
式中:ap＋bp＝1，aq＋bq＝1。P0、Q0和V0分别为额定有功、额定无功和额定电压值；P、Q和V分别为实际有功、实际无功和实际电压值。

假定电压幅值的理论计算结果Vfor与实际值的偏差服从均值为0、标准差为σ的正态分布，由此得到实际负荷的概率密度为:

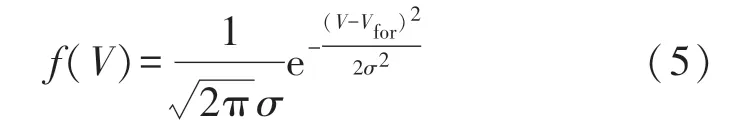
假定该工况的发生概率为λ1，结合上述两式可以求解出该工况下负荷的有功功率和无功功率的期望值。

接着，建立发电机不确定性模型。对于PV 节点，机端电压可通过下式计算得到:

式中:ΔV为电压变化量。同理，实际机端电压的概率密度仍可基于式(5)表示，假定该工况的发生概率为λ2，结合式(6)能够求出PV 节点机端电压的期望值。

最后，求解各常见工况的发生概率。将概率分布函数分为7 段，其概率和为1，且各区间宽度均为标准差。基于蒙特卡洛随机抽样法[16]得到第s个场景下的标准化概率ρr(s)为:

2.2 多目标无功优化控制模型的建立

2.3.1 目标函数

本文以全网网损最小以及PV 节点调节偏差最小为目标进行计算，计算公式分别如式(8)、式(9)所示:

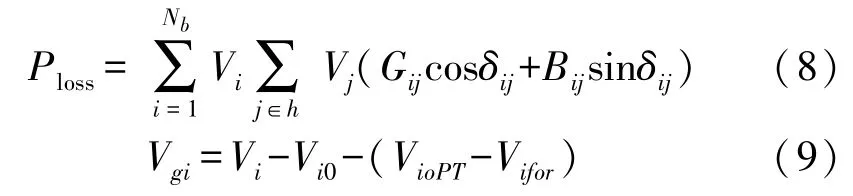
式中:Vi为节点i的电压实际值，j∈i为与i连接的全部节点，Nb为支路数，Gij、Bij、δij分别为i、j间的电导、电纳及相角差；Vi0为第i个节点的机端电压量测值；Vifor、VioPT分别为在状态估计和状态估计断面上优化计算求解出的第i个PV 节点的机端电压计算值；Vgi为第i个节点调节偏差向量。

进一步地，求解得到多目标无功功率优化控制目标特性方程为:

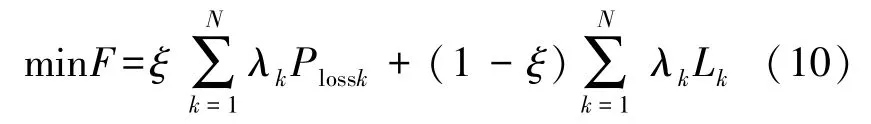
式中:ξ为比重系数，N为状态估计模糊工况数，λk、Lk、Plossk分别第k个工况的发生概率、节点调节偏差以及网损。

2.3.2 约束函数

节点i有功、无功功率基本约束特性为:

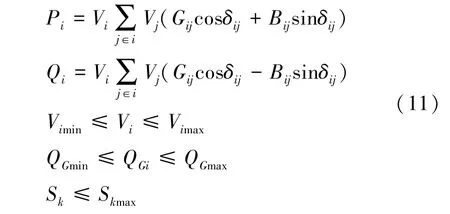
式中:Vimin、Vimax分别为该节点的电压下、上限值；QGmin、QGmax分别为发电机无功的下、上限值；Skmax为支路k视在功率的约束值。

考虑备用机组的存在，对参与优化的区域增加冗余约束，其约束特性方程为:

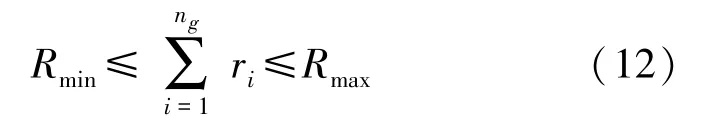
变量自身约束特性方程为:

备用变量对应的目标函数为:

式中:ng为备用数量，ri为第i台机组的备用容量，f(ri)为机组i的备用费用函数。

最后，对断面场景进行约束。稳定断面一般是一组电气支路的潮流和，而支路潮流是电气节点电压角度的线性方程式[17]，则稳定断面k的潮流值如下式所示:

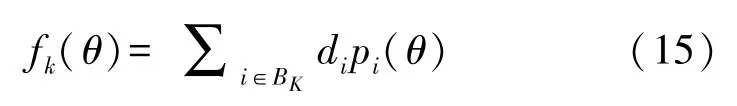
式中:Bk代表电气支路组成，di为支路潮流方向，1或者－1。

断面潮流值的线性约束方程为:

3 基于改进QPSO 的电压优化控制算法

3.1 改进QPSO 算法的提出

QPSO 算法通过构造DELTA 势阱场，以粒子吸引点为中心，引入平均最优位置实现粒子位置的更新，得到粒子位置X的进化公式为[18]:

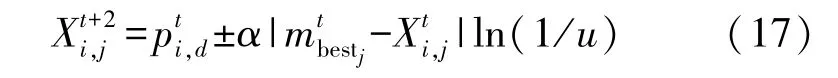
式中:i，j是i粒子的第j维，t为当前迭代次数；为第t次迭代第i个粒子第d维的局部吸引子；u为[0，1]上均匀分布的随机数；α为收缩扩张系数；为个体最优位置全部粒子的平均数。

本文基于自适应权重系数对平均最优位置进行更新，拓宽粒子知识的搜索区域，这样一来，既提高了粒子的自适应能力，又能够加快非线性化的检索过程[19]。

(1)优化平均最优位置

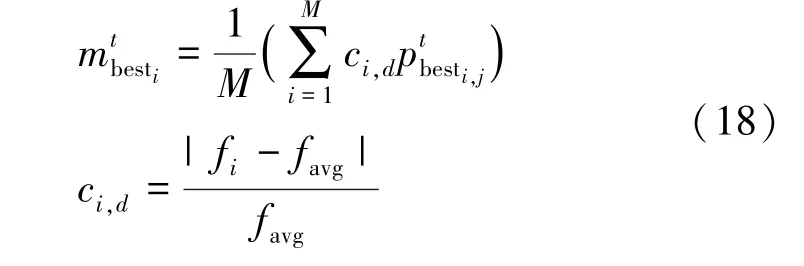
式中:fi、favg分别为当前粒子和平均粒子的适应度值；ci，d为随着fi变化而自适应的权值。

(2)自适应调节α系数

收缩－扩张系数α在QPSO 算法中的作用等价于PSO 算法中的惯性权重系数[20]。传统固定值/线性减少策略下，粒子的α值相等，自适应性能较差。为此，本节提出了一种非线性自适应优化方法:

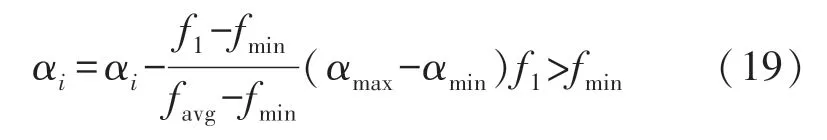
式中:αmax、αmin分别为α的最大、最小值；fmin表示粒子群的最小适应度值。其中，当fi＞favg时，表示粒子的位置接近全局最优，其α值取较小值便于进行更细致的局部搜索，而其他粒子则赋予较大的步长，以加快整体的寻优速度。

(3)改进QPSO 算法的提出

本文结合差分进化算法和粒子群算法，计算每一代粒子的变异概率P(t)为:

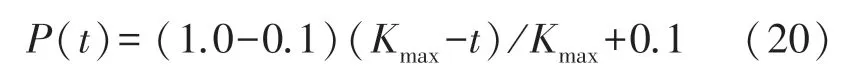
式中:Kmax为最大迭代次数。

算法由变异、交叉和选择三个部分组成。假设每个粒子个体，其变异量为:

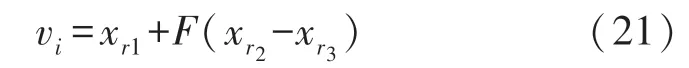
式中:xi，i＝1，2，…，N，r1、r2、r3∈[0，1]是常实数，用来控制差异量大小。

接着，基于式(22)増加群体的多样性:

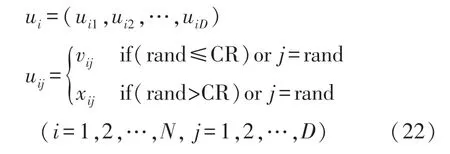
式中:ui表示第i个粒子第j维度的交叉量，CR 为交叉概率，CR∈[0，1]。

经过上述处理后，下一代个体的适应度值能够优于当前个体，不仅仅满足了种群的多样性要求，又能够促进种群进化。

3.2 算法特性验证

本文分别选用群体规模大小为20、40、80 的群组来测试算法对粒子规模的可扩展性，选用Griewank 函数、Rastrigin 函数以及Schaffer 函数三种标准测试函数对基于差分进化的改进QPSO 算法和原算法在收敛性和速度方面的性能差异进行测试，计算过程中，设定三种函数的维数分别为30、30、2。设定Kmax为2 000，对不同算法下各函数实例各运行50 次，记录最优目标函数值并求解出其均值和标准差，结果如表1 所示。

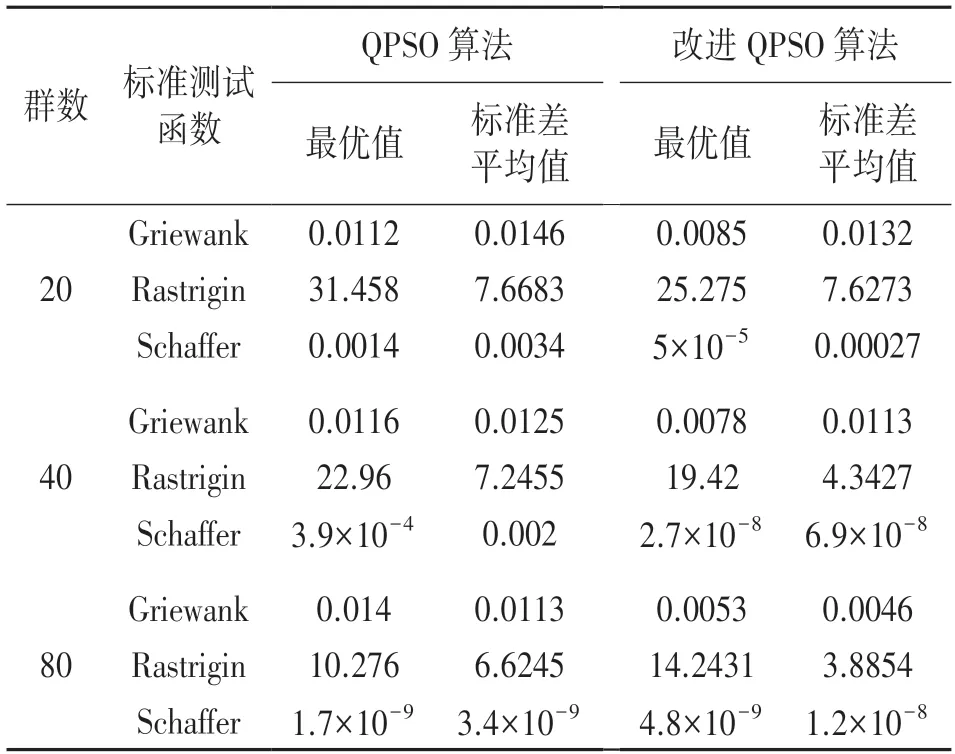
表1 不同算法下各函数的特性比较

从表1 的测试结果来看，相比于原算法，改进QPSO 算法在收敛速度上得到明显提高，具有更好的收敛性。此外，随着种群数量的增加，全局搜索能力也越强。

4 案例分析

以某日受不确定影响因素干扰的系统运行数据为例，应用本文所提模型和算法，以总体满意度最大为目标进行无功电压优化计算，得到系统网损变化特性曲线如图2 所示。

从图2 的仿真特性曲线来看，考虑电网随机性的无功优化控制算法，其网损量要显著低于普通潮流计算结果。图2 中，在用电高峰期阶段，优化后的网损值要稍高于优化前的网损值，这是由于在用电高峰期为确保电能质量，设置了该时段无功优化电压的上、下限为0.9～1.1 区间所导致的，但不影响优化算法的整体优化效果。

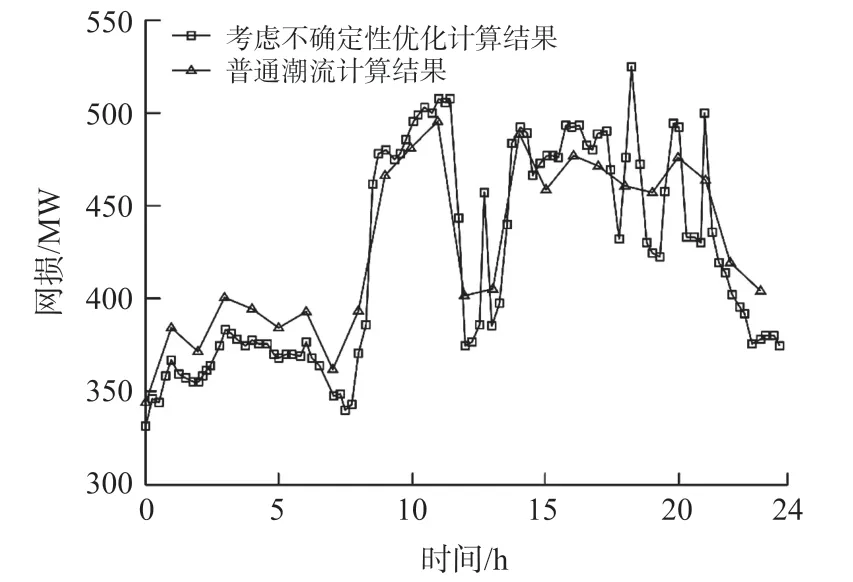
图2 网损变化特性曲线

本文分别以网损期望值隶属度、PV 节点调节偏差小期望值隶属度以及总体满意度最大为目标，对优化特性进行分析，结果如表2 所示。

表2 不同优化方案下的隶属度值

从表2 可以看出，以单一目标进行优化控制时，可以使得本目标的隶属度达到1 左右，但其余目标的隶属度相对较小，这是由于电网中网损和电压的分布性特性所决定的。本文所提出的优化改进QPSO 算法虽然不能使得网损期望值、PV 节点调节偏差小期望值以及总体满意度都达到最优，但是能够使得总体满意度最大，体现了算法对不同目标值的协调作用，以实现总体目标最优。

以五个变电站节点为例，对优化前后的节点电压的大小进行比较，结果如表3 所示。

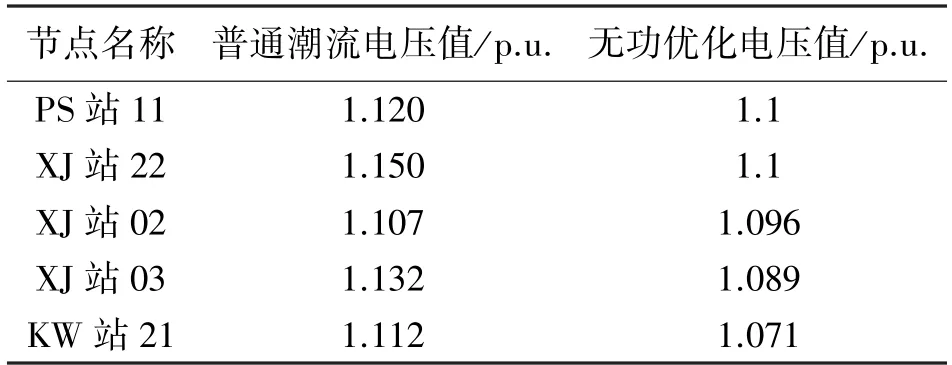
表3 不同节点电压优化结果比较

从表3 来看，采用普通潮流计算方法求解得到的XJ 站22 节点电压最大可达1.15 p.u，XJ 站03节点电压最大可达1.13 p.u，而考虑电网随机性的无功优化控制方法，对于各个变电站节点电压均保持在0.9 p.u～1.1 p.u 之间，稳定性较好。

5 结论

本文充分考虑电网动态平衡的特性，提出了一种考虑随机因素的无功优化计算系统模型，通过对初始断面的不确定性场景进行选取，求解出常见工况的发生概率，基于网损大小以及电压调节偏差量，提出了一种多目标无功功率优化控制算法。通过算例仿真分析验证了所提出的模型及算法在协调系统不确定性和PV 节点调节偏差之间的关系的可行性和实用性。