最优化方法应用于裂变核反应理论计算的研究

田 源，续瑞瑞，张 玥，陶 曦，王记民，金永利，张 智，孙小东，葛智刚

(中国原子能科学研究院 核数据重点实验室，中国核数据中心，北京 102413)

核数据是核能、核工程、核技术应用和核科学研究的基础数据，虽然实验测量是获得核数据的基础，然而，受各种因素的限制(如实验成本高，更重要的是在实验上所要求的入射粒子种类和能量、靶核制备以及某些测量条件等方面并不总能实现)，因此，在核装置的设计与测试过程中，实验常被用来精确定量少量关键核素的重要反应与结构核数据，而绝大部分核工程所需数据须通过理论计算完成。要使用核反应模型计算核数据，一方面需尽可能准确描述相应核反应的反应机制，另一方面则是快速有效确定核反应模型中的参数。本项目围绕裂变核反应模型，利用先进的最优化方法确定模型中的参数，并应用于锕系核中子诱发裂变反应核数据的研究。

目前国际上最著名的核反应模型程序系统有TALYS[1]和EMPIRE[2]等。我国采用的FUNF[3]是由中国核数据中心张竞上研究员开发研制，具有我国自主知识产权的裂变核反应程序系统，可用于计算和分析能量在20 MeV以下中子诱发易裂变核反应相关的数据。多年来，一直在我国核数据理论研究过程中发挥着重要的作用。FUNF的理论框架包括光学模型、Hauser-Feshbach模型以及激子模型等。裂变核反应模型总的可调参数多达50个。因此，需通过一些先进的最优化方法，根据已知的核反应实验结果，确定裂变核反应模型的参数，并最终用于计算裂变核反应数据。

最优化方法是一种数学方法，它是研究在给定约束条件下如何寻求某些因素(或量)，以使某一(或某些)指标达到最优的一些方法的总称。本工作要在裂变核反应模型的约束条件下，通过不同的调参方法调整模型中的参数，使得模型计算的裂变核反应数据，如反应道的截面、出射中子的角分布和能谱、各种出射粒子的双微分截面等，与已知的实验结果的符合程度达到最优。目前较常用的的调参方法有梯度下降法[4]、牛顿法[5]、共轭梯度法[6]以及启发式优化算法等。这些方法各有优缺点，分别适用不同的调参环境，适当的调参方法能大幅提高参数调优的计算成本。20世纪70年代，欧洲核子研究中心(CERN)的科学家Fred James综合了多种最优化方法建立了寻找方程最小值的物理分析工具MINUIT[7]。迄今为止，MINUIT方法已经被广泛用于分析实验数据和建立理论模型。美国的EMPIRE程序将MINUIT方法用于参数调节。

对于简单的核反应模型，参数一般较少，计算也相对简单，一般的调参方法如格点法、随机法通过不断的尝试即可找到最优的参数组。FUNF裂变核反应模型不仅约有50个参数，计算也相对复杂，单次计算时间随着入射粒子能量的不同，可能是几秒也可能多达数分钟。因此本工作将FUNF裂变核反应模型与MINUIT方法相结合，并引入并行计算等方法，研究如何将最优化方法用于调节FUNF裂变核反应模型中的参数，并改进裂变核反应数据。

1 裂变核反应理论模型

当中子入射能量在20 MeV范围内时，核子与核发生反应的全过程可被划分为3个阶段：独立粒子阶段、复合系统阶段以及发射粒子后形成剩余核阶段。独立粒子阶段中，入射粒子在靶核的势场作用范围内发生散射与吸收，可采用光学模型进行描述；进入复合核阶段中，入射粒子与靶核相互作用，随着入射粒子能量的变化，入射粒子与靶核中核子发生能量交换的可能性非常丰富多样，该阶段可发生直接反应、复合核粒子发射反应以及预平衡粒子发射反应，因此，发展了包括直接反应、蒸发模型、Hauser-Feshbach模型、激子模型等一系列核反应理论来描述该阶段，此外，中子与锕系核相互作用的过程中，需特别考虑核裂变的贡献对核反应数据的影响；最后一个阶段，在上一个反应阶段的基础上，复合核系统发射粒子后变成剩余核。张竞上研究员研制的中子与锕系核反应计算程序FUNF，包含了快中子能区内锕系核的主要核反应过程，考虑3次粒子发射过程，多年来已成功为核工程用户解决多项锕系核反应数据问题，本工作中锕系核反应中子数据模型计算工作由该程序完成。

1.1 光学模型

光学模型是核反应过程的基础与起点，控制着之后的多项核反应物理过程，该模型的引入成功描述了入射粒子在靶核势场中进行的散射与吸收的过程。光学模型所建立的复数形式势场，结合求解薛定谔方程可用来描述散射过程中的多个物理量，包括全截面、反应(去弹)截面、弹性散射截面及角分布和穿透系数，并为复合核计算提供重要的穿透系数。

在FUNF程序中，中子与锕系核全套核反应数据计算中，光学模型势采用对实验数据描述准确度较高的唯象光学势[8]，对应的一般形式如下：

U(r)=Vr(r,E)+iWs(r,E)+iWv(r,E)+

[Vso(r)+iWso(r)](s·l)+Vc(r)

(1)

其中：Vr(r,E)为实部中心势；Ws(r,E)为虚部势的面吸收项；Wv(r,E)为虚部势的体吸收项；Vso(r)为自旋轨道耦合势的实部；Wso(r)为自旋轨道耦合势的虚部；s、l分别为入射粒子自旋角动量与轨道角动量；Vc(r)为库仑势；E为入射中子在实验室系下的能量，MeV。

式(1)中，实部中心势可表示为：

(2)

式(2)中V(E)可表示为能量依赖关系：

V(E)=V0+V1E+V2E2+

(3)

其中：A为靶核质量数；N为靶核中子数；Z为靶核电荷数。

对应虚部势的面吸收形式为：

(4)

(5)

对应虚部势的体吸收形式为：

(6)

Wv(E)=max{0,U0+U1E}

(7)

对应自旋轨道耦合势实部Vso(r)和虚部Wso(r)分别表示为：

(8)

(9)

其中：ar、as、av和aso为光学模型势的对应项中的弥散宽度参数；Rr、Rs、Rv和Rso为光学模型势的对应项中的半径参数，单位为fm，对应计算公式为：

(10)

其中，i=r,s,v,so，对应半径参数。

此外，库仑势对应形式为：

(11)

式中：z、Z为入射粒子和靶核的电荷数；Rc为库仑半径。因此，可调的光学势参数为12个深度参数、5个半径参数、4个弥散宽度参数，其中有12个参数对截面较为敏感。

1.2 复合核模型

当入射粒子被靶核吸收后，核反应进入第2个阶段，即复合核阶段。在该过程中，入射粒子与靶核发生多次相互作用，不断将能量传递给靶核，最终达到统计平衡的状态，与靶核融合形成新的原子核，被称为复合核过程，其作用时间最长，约10-15s。进入平衡态的复合核通过发射粒子而衰变，剩余核处于分立能级的激发态，实验表明，截面与原子核的初态和末态的激发能、自旋、宇称等性质直接关联，考虑了角动量守恒与宇称守恒的Hauser-Feshbach理论被发展用来描述该部分贡献，结合宽度涨落修正可更好描述真实的实验测量。

当入射粒子能量增大，二次核反应过程开放，预平衡核反应过程变得不可忽略。该过程中粒子与靶核作用时间介于直接过程与平衡过程之间(约10-22～10-16s)，粒子与靶核中少量核子发生能量交换，在体系还未达到统计平衡状态时就发射粒子退激。因此，Griffin等在Feshbach的中间结构理论基础上提出了激子模型用以描述不同激子态条件下的粒子发射过程。

在上述两种理论体系基础上，张竞上等发展的统一的Hauser-Feshbach与激子模型在保证了角动量守恒与宇称守恒的前提下，可考虑预平衡粒子道分立能级态的贡献，对于准确计算中子能谱等物理量有重要价值，并成功应用在裂变核反应程序FUNF中。

一般，复合核过程中考虑的核反应包括中子辐射俘获(n,γ)和中子非弹(n,inl)、(n,p)、(n,d)、(n,t)、(n,α)、(n,2n)、(n,3n)等，这些核反应互相竞争。在实际工作中，为考虑各类出射粒子反应道的发射概率，除输入各复合核低激发态分立能级、自旋、宇称等信息外，复合核相关模型中还引入能级密度、对修正等参数考虑高激发态的核结构与核内核子运动形态，从而确定各反应道的分配比例。另一方面，与中重核反应不同，中子与锕系核相互作用的核反应还需考虑核裂变截面(n,f)的贡献，该反应同样与其他核反应道竞争。FUNF程序中，通过唯象引入3个彼此独立的裂变位垒来表征整个核反应中的裂变系统，基于Bohr-Wheeler公式，通过调整各裂变位垒的高度、曲率形状、垒上能级密度、对修正等参数，确定裂变位垒形状，计算得到裂变概率，在与其他反应道竞争的条件下，共同确定(n,f)、(n,nf)、(n,2nf)3个裂变道截面的大小。

因此，复合核模型中涉及到的可调参数包括11个反应道的能级密度、对修正参数，其中7个反应道的参数灵敏度较高，共计14个；8个反应道的巨共振参数，其中2个反应道的参数较敏感，共计12个；3个裂变道对应的位垒高度、曲率形状、垒上能级密度、对修正等参数，共计12个。合计至少需要调整38个参数用于计算各反应道的截面数据。

1.3 直接核反应

形成复合核并非是所有核反应的必经阶段。当入射粒子能量较高时，入射粒子与靶核通过很短的相互作用时间(约10-19～10-21s)发生反应，具体过程包括：1) 入射粒子将能量传递给靶核表面或者内部的1个或多个核子，并逃出该复合系统；2) 入射粒子将能量传递给靶核后飞出该系统，靶核得到部分能量而产生集体激发，并发生集体转动或振动；3) 入射粒子与靶核发生多次碰撞，最终逃出该复合系统。

在直接反应模型中，通常采用扭曲波玻恩近似(DWBA)与耦合道方法对直接反应的贡献进行计算，其中DWBA用来描述球形核或近球形核，耦合道方法用来描述变形核。在中子与锕系核反应计算中，直接核反应的贡献在中子非弹截面中贡献较大，由于锕系核受到激发后，普遍存在集体转动能级，因此，一般采用耦合道方法来计算该部分工作，本工作将采用ECIS程序完成直接非弹耦合计算的任务[9]。

2 最优化方法

2.1 MINUIT方法

MINUIT是由CERN的物理学家Fred James在20世纪70年代建立的用于寻找方程最小值的物理分析工具。MINUIT中已包含了多种先进的最优化方法，如蒙特卡罗随机法、单纯形算法以及变尺度法等。经过多年的发展，这套工具已有Fortran、C++、JAVA以及Python等多个版本，在多个领域被广泛用于调参并取得了巨大的成功。

MINUIT方法中不同的最优化方法可分别针对不同调参环境做出选择。

1) 蒙特卡罗方法[10]，这种方法通过蒙特卡罗随机抽样的方法寻找参数。主要用于调参初期参数初始值不确定的情况下，通过随机扫点找到可能存在的多个极小点。

2) 可变单纯形算法[11]，这种方法又名Nelder-Mead方法，是常见的直接搜索型非线性优化方法，由Nelder和Mead在1965年提出。此方法利用单纯形进行搜索(单纯形是N维空间的广义三角形)。可变单纯形算法在每个顶点对用户提供厄函数进行求值，然后发现更好的点来迭代收缩单纯形。当到达预期的边界或其他终止条件时，方法终止。由于未利用任何求导运算，算法较简单，但收敛速度较慢，适合变元数不是很多的方程求极值。

3) MIGRAD方法[12]，MIGRAD方法是基于Fletcher提出的变尺度法，它克服了梯度法收敛速度慢和牛顿法计算量、存储量大的特点，被公认为是求解无约束优化问题最有效的算法之一。

2.2 MINUIT用于FUNF参数优化

图1为MINUIT方法用于调整FUNF裂变核反应程序参数的流程图。第1步，将经验参数作为初始参数代入到FUNF裂变核反应模型中得到1组裂变核反应数据，通过比较得到与已知的实验结果偏差。第2步，通过下山单纯形或MIGRAD变尺度法找到1组参数，再代入到模型中，计算出1个新的实验数据的偏差。若偏差有所减小，则接受这套新的参数；若偏差增大，则利用下山单纯形或MIGRAD变尺度法重新找到1组参数。重复第1、2步，直到满足FUNF裂变核反应模型计算的结果与实验数据的偏差小于预设的条件，这时得到参数组则是需1个极小解。利用蒙特卡罗法随机生成1组新的参数组，重复第1、2步，得到1组新的极小解。反复找到几组极小值后，比较极小值最终确定FUNF裂变核反应的最优解。

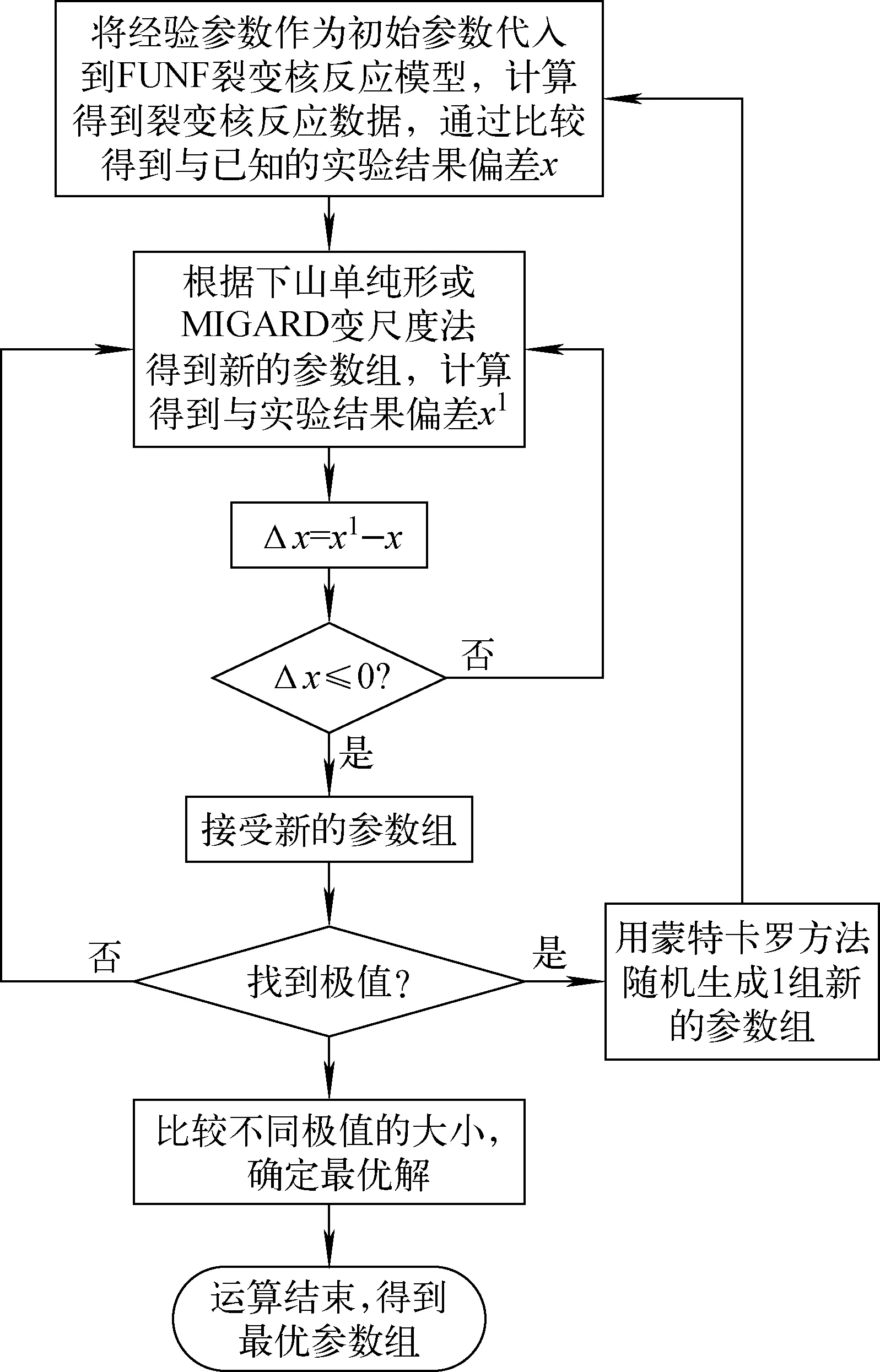
图1 MINUIT用于调整FUNF裂变核反应程序参数的流程图Fig.1 MINUIT flowchart for adjusting parameters of FUNF fission nuclear reaction program

2.3 参数优化准则

首先，在调参过程中，判断参数是否合格的1个重要结果就是最小均方根：

(12)

其中：σExp为需要符合的实验结果；σth为理论计算的结果；σerr为误差权重。对于裂变核反应，首先可通过调研已有实验数据和评价数据，确定各反应道的截面数据σExp。不同的实验测试之间可能存在分歧，且不同实验给出的误差范围也不尽相同。σerr的选取决定了理论计算趋向于哪个实验结果，因此这个量的选取尤为重要。需要结合实验数据的复杂程度、实验的误差范围以及其他评价数据库的评价结果和评价误差最终确定调参过程中采用的误差权重。

其次，在FUNF裂变核反应程序中，光学模型是所有计算的基础，直接反应、复合核反应和预平衡反应均依赖光学模型的计算结果。因此在调参顺序上，首先根据总截面、弹性截面、弹性角分布等数据确定光学模型的参数；接着固定光学模型参数，再根据各反应道的数据信息同时自动调整能级密度、对修正、巨共振以及裂变位垒等参数；最后在所有截面与实验数据基本一致的情况下，再对个别参数通过提高权重，改变参数范围、步长的方法进一步精调。最终得到最优化参数组和理论计算的数据结果。

判断参数优化要遵循以下3个判据。1) 参数是否具有物理意义，FUNF裂变核反应程序中的所有参数有各自物理意义，因此每个参数均只能在合理的范围内变化，超出这个范围会导致非物理的结果出现。2) 是否得到χ2值最优。由于涉及参数较多，系统χ2可能存在多个极小值，需多次尝试调参得到最优解。3) 与实验结果相比，理论计算结果是否具有好的视觉符合。由于实验结果较多，且结构相对复杂，需通过观察判断理论计算的各反应道的截面是否能较好符合实验结果。

2.4 并行化调参

FUNF模型由多个核反应模型组成，结构相对较复杂，计算时间较长，一般在5～10 s之间。涉及到的参数可能多达50个。因此即使在MINUIT方法的辅助下，单核的调参时间也可能高达数天。若同时对多个核素进行拟合，调参时间将成倍增长，因此需将FUNF+MINUIT的调参程序进行并行化加速，从而缩短时间，提高效率。消息传递接口(message passing interface, MPI)是科学计算中常用的编程模型。在这种并行编程中，每个控制流均有自己独立的地址空间，不同的控制流之间不能直接访问彼此的地址空间，须通过显式的消息传递来实现。这种编程方式是大规模并行处理机(MPP)和机群(Cluster)采用的主要编程方式。由于消息传递程序设计要求用户很好地分解问题，组织不同控制流间的数据交换，并行计算粒度大，特别适合于大规模可扩展并行算法。计算过程中发现，通过将MPI与MINUIT相结合，随着CPU线程数量的增加，FUNF裂变核反应程序的调参时间成倍减小，计算效率成倍增加。

2.5 最优化方法的选择

图2为用可变单纯形算法(SIMPLX)和变尺度法(MIGRAD)对光学模型参数(OPM)和复合核模型参数(CM)优化的迭代次数。多核并行的迭代次数为每个线程的迭代次数的平均值。迭代次数越少，说明最优化方法能更快的找到参数的最优解。复合核模型的参数有38个，大于光学模型的12个参数，因此需花费更多的迭代次数得到最优化参数组。无论是针对光学模型调参，还是调整复合核模型的参数，变尺度法均好于可变单纯形算法。另外，通过MPI方法实现了并行化调参。在包含28个线程的小型服务器帮助下，调参效率提高了约20倍左右，且计算效率还会随着线程的增加继续提高。因此在计算过程中，主要采用并行的变尺度法(MPI-MIGRAD)进行调参，只有在变尺度法难以收敛时才考虑采用其他的最优化方法辅助调参。

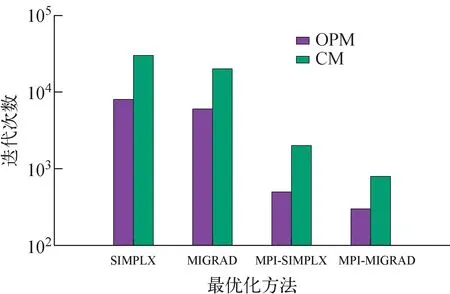
图2 不同最优化方法在单核和多核并行的迭代次数Fig.2 Number of iterations of different optimization methods in single-core and multi-core parallelisms

3 结果与讨论

利用最优化方法调整FUNF裂变核反应程序的相关参数，并得到与中子诱发238U核反应的主要反应截面相符的理论计算结果。

首先，通过参考EXFOR实验核反应数据库和ENDF核反应评价库中快中子区的截面结果收集中子诱发238U的核反应数据。FUNF裂变核反应程序能计算的反应道包括(n,tot)、(n,γ)、(n,inl)、(n,2n)、(n,3n)、(n,f)、(n,p)、(n,d)、(n,t)和(n,α)等。目前实验测量主要集中在(n,tot)、(n,inl)、(n,2n)、(n,3n)、(n,γ)和(n,f)这几个反应道中。而带电粒子出射道中的(n,d)和(n,t)反应道无实验数据，(n,p)和(n,alpha)反应道的实验数据较少，无法用于指导参数调优工作。(n,3n)反应道的实验数据也相对较少。因此，本工作的参数调优主要依托于(n,tot)、(n,γ)、(n,inl)、(n,2n)和(n,f)的实验数据引导，并参考ENDF评价库的部分结果。

然后，将MINUIT方法与FUNF裂变核反应程序相结合。先根据总截面、弹性角分布以及非弹截面确定光学模型参数；然后通过拟合各反应道的截面结果，得到能级密度、对修正、巨共振以及裂变位垒参数值；最后针对个别参数进行精调，得到1组可再现中子诱发238U核反应截面数据的FUNF参数组。

表1为通过拟合总截面、弹性散射角分布以及非弹截面并使得χ2最小，最终得到的光学模型参数。其中ai为弥散半径，ri为半径，U、V、W分别为BG光学势的强度参数，i=r、s、v、so、c分别表示实部、表面虚部、体虚部、自旋轨道耦合项以及库仑项。观察发现，各参数均在合理的物理区间范围内。图3为238U(n,tot)反应截面，理论计算结果与实验测量数值和评价数据基本符合。说明得到的光学模型参数是适用的。

表1 FUNF采用的光学模型参数Table 1 Parameters of optical potential model of FUNF

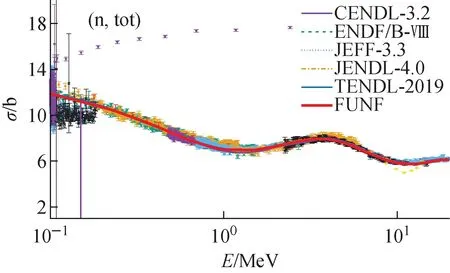
图3 238U(n,tot)截面实验数据及评价数据Fig.3 Experimental data and evaluation data of 238U(n,tot) cross sections

表2为FUNF计算程序中的参数，其中LD为能级密度参数，PC为对修正参数，FB为裂变位垒参数，后面的数字0～10分别表示(n,γ)、(n,inl)、(n,p)、(n,α)、(n,d)、(n,t)、(n,2n)、(n,3n)、(n,f)、(n,nf)和(n,2nf)这些反应道；CP表示裂变位垒曲率半径，CFLD表示裂变能级密度系数，后面的数字0～2表示裂变道中的(n,f)、(n,nf)和(n,2nf)这3个反应道。图4～8分别展示了(n,inl)、(n,2n)、(n,3n)、(n,f)和(n,γ)反应道的理论计算结果与实验数据及评价数据的比较。图中各种不同颜色符号表示实验测量数据，不同颜色线段代表不同的评价库的评价数据，粗红线为FUNF裂变核反应程序计算的结果。调参最终得到所有反应道的χ2之和最小。观察发现，各参数均在合理的物理区间内，且理论计算的结果与实验数据和评价数据保持一致。因此，通过MINUIT最优化方法得到的FUNF裂变核反应程序用于计算20 MeV以内中子诱发238U核反应数据的参数合理有效。

表2 FUNF采用能级密度、对修正以及裂变位垒参数Table 2 Level density, pairing and fission barrier parameters of FUNF

图4 238U(n,inl)截面实验数据及评价数据Fig.4 Experimental data and evaluation data of 238U(n,inl) cross sections

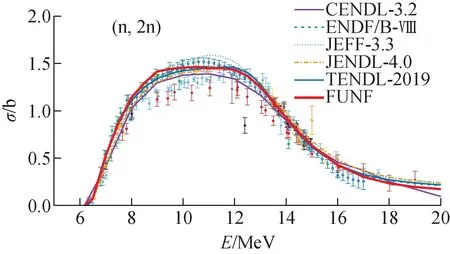
图5 238U(n,2n)截面实验数据及评价数据Fig.5 Experimental data and evaluation data of 238U(n,2n) cross sections

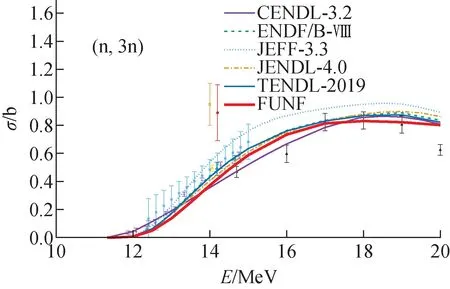
图6 238U(n,3n)截面实验数据及评价数据Fig.6 Experimental data and evaluation data of 238U(n,3n) cross sections

4 总结

对于简单的核反应模型，参数一般较少，计算也相对简单，一般的调参方法如格点法、随机法通过不断的尝试即可找到最优的参数组。裂变核反应的反应机制十分复杂，需由几个不同核反应模型共同描述，因此需同时对大量参数进行优化才能正确描述裂变核反应数据。

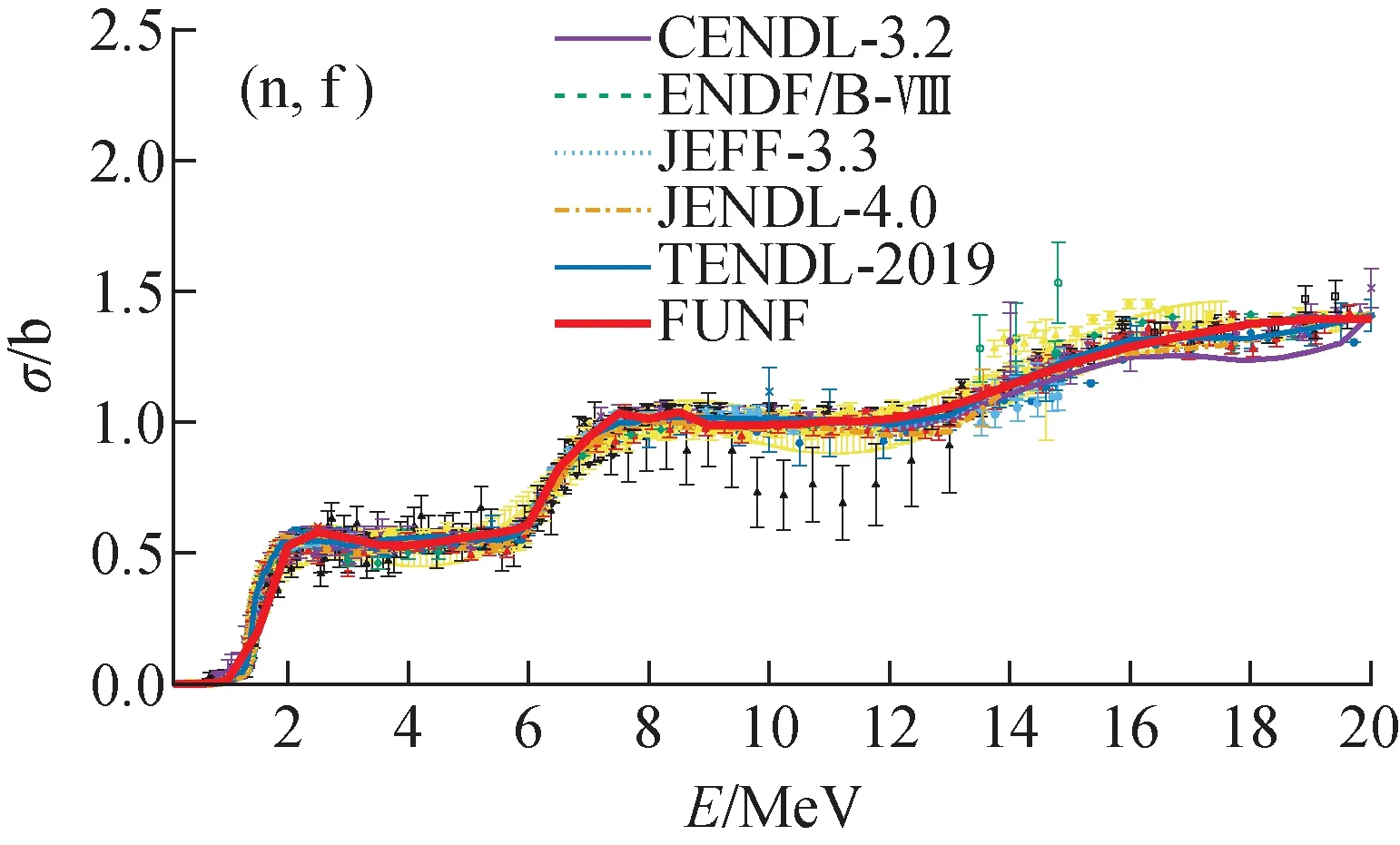
图7 238U(n,f)截面实验数据及评价数据Fig.7 Experimental data and evaluation data of 238U(n,f) cross sections

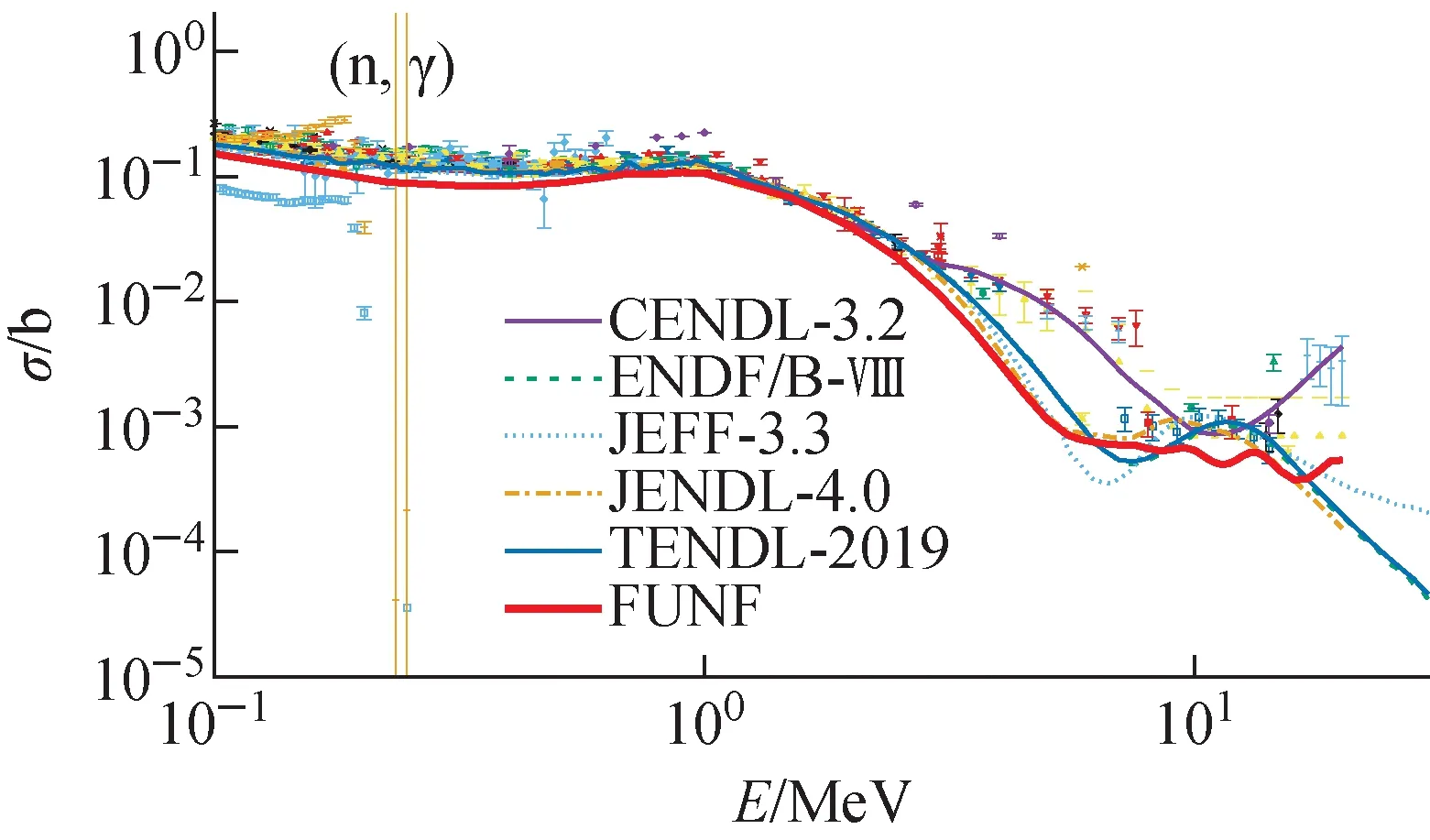
图8 238U(n,γ)截面实验数据及评价数据Fig.8 Experimental data and evaluation data of 238U(n, γ) cross sections

在FUNF裂变核反应模型基础上，首先将最优化方法MINUIT与FUNF相结合，实现多参数的自动调参。FUNF裂变核反应程序由球形光学模型、统一的Hauser-Feshbach和激子模型理论等核反应模型共同构成。FUNF涉及到的参数包括粒子的光学势参数、巨共振参数、能级密度参数、对修正参数以及裂变位垒和位垒曲率等参数，多达50个。FUNF程序的计算时间也相对较长，所需调参时间可能长达数天。为提高调参效率，采用MPI的并行计算方法，在多核心并行计算的帮助下，将计算效率提高了20倍左右，且计算效率还可随线程数的增加继续提高。

在这些工作的基础上，针对238U的裂变核反应进行了初步的计算。结果显示，通过MINUIT最优化方法得到的FUNF参数能很好描述238U的裂变核反应数据。后期将继续优化程序，进一步提高调参的效率和参数的精确度。并对相关的裂变核反应展开应用，提高我国裂变核反应数据的精度。