区域环境规制、技术创新与绿色全要素生产率——基于长江经济带省级面板数据分析

郭凯路 ，李世祥

（1. 太原师范学院 管理系，山西 晋中 030619；2. 中国地质大学（武汉） 公共管理学院，湖北 武汉 430074）

制度，是社会的博弈规则，是人为设计、形塑人们互动关系的约束准则，它包含着正式规则和非正式规则[1]。环境规制即现代经济社会为避免生态污染超过环境容量的一种制度安排[2]。区域资源和环境条件是制定该区域环境规制的重要基础条件，脱离了生态环境本体，环境规制对于区域生产力的提升则有可能存在一定偏差，难以使生态环境与经济发展相协调。人们利用自然资源满足工业化生产对原材料需求的同时，生态环境的压力却日益增加。因此，环境规制及其影响是当前国内外的研究热点和难点。

1 文献综述

西方学术界曾长期认为环境规制在一定程度上提高了生产生活的成本，降低了企业参与市场活动的竞争力，环境规制带来的消极效应基本抵消，甚至大过了其产生的积极效应[3]。Porter & Linde[4]对此持相反观点，他们在1995 年发表的《迈向环境——竞争力关系的新理念》一文中，基于动态的视角指出环境规制能够激发企业的技术创新，企业也因此获得了创新补偿，进而弥补遵循环境规制带来的额外成本，促进了企业的生产率，有利于企业竞争力的提升。在此背景下，“波特假说”掀起了对环境规制利弊的热烈讨论。大量文献对此展开研究，从不同角度、不同地区和不同发展阶段等方面对“波特假说”进行论证，这进一步说明，环境规制与地区技术创新和经济发展质量的关系研究内嵌于经济社会发展与生态环境保护的矛盾中。目前，关于环境规制是否推动了科技进步，越来越多的研究表明，“波特假说”对于处于不同发展阶段的国家或地区存在很大差异。即认为“波特假说”是基于美国等发达国家而提出的，其高度发达的资本主义市场化经济和对技术创新前沿技术的占有均支持了“波特假说”的成立。而对于“波特假说”在中国或者其他发展中国家是否成立，学术界仍存在争议[5]，究其原因，有学者认为中国低效运转的市场还不足以支撑类似排污权交易机制的“完美”运行，而整体较弱的环境规制也不能与排污权交易机制“完美”运行相匹配[6]。

与此同时，国内学术界对环境规制是否促进绿色全要素生产率尚未达成统一的共识，从宏观经济学的角度看，全要素生产率是反映地区经济效率和技术进步的重要指标，而考虑了污染排放等非期望产出的绿色全要素生产率则更多程度上反映了地区经济效率的绿色化。从国家宏观层面看，蔡乌赶和周小亮[7]研究发现三种环境规制（命令控制型、市场激励型、自愿协议型）对绿色全要素生产率存在不同的影响，且就中国具体实证角度看，环境规制对绿色全要素生产率的间接作用受地区技术创新、要素结构和FDI 水平的异质性影响，影响效应最大的路径是要素结构。从省际中观层面看，赵明亮等[8]研究发现环境规制对黄河流域上中下游的不同地区绿色全要素生产率存在影响的差异性。从工业行业微观层面看，李斌等[9]、陈超凡等[10]、张峰和宋晓娜[11]等学者针对中国36 个工业行业进行实证分析，均发现环境规制对工业绿色全要素生产率存在异质性影响，且环境规制强度存在“门槛效应”，即环境规制强度介于1.999 和3.645之间时，加大环境规制力度有利于促进工业发展方式的转变，而当环境规制强度跨过门槛值3.645 时，加强环境规制强度会对工业发展方式的转变产生负面作用。

关于技术创新与绿色全要素生产率相互关系的研究，国内尚处于起步阶段。朱金鹤和王雅莉[12]通过模型检验提出在全国和省级层面以及不同强度的环境规制下，技术创新水平对绿色全要素生产率均存在不同的影响。从地级市层面来看，获批低碳试点的城市能够直接促进城市绿色全要素生产率，且低碳试点政策能够通过提升城市创新水平，进而促进产业转型并间接提升城市绿色全要素生产率，但产业结构转型的间接效应并未得到验证[13]。从工业微观层面来看，技术创新以年均1.047%的增长速度成为驱动工业绿色发展的主要动力，驱动贡献为47%[14]。

综上所述，已有文献分别从不同角度检验了环境规制、技术创新与绿色全要素生产率的相互影响关系，多数研究结果倾向于不同的发展阶段、差异性的社会经济条件和制度环境等客观因素使得三者之间关系存在相互间异质性影响效应。基于此，本文选择长江经济带这一战略区域进行实证研究，通过测算长江经济带2005—2017 年省际绿色全要素生产率，并利用熵值法测算区域环境规制综合指标值，构建动态平衡面板数据，利用面板向量自回归模型检验长江经济带区域环境规制、技术创新与绿色全要素生产率之间的动态互动关系。在“长江大保护”前提下，合理的环境规制是促进长江经济带高质量发展的关键制度保障。因此，本研究具有重要的理论和实践意义，可为长江经济带生态优先、绿色发展提供参考依据。

2 数据来源与处理

构建动态平衡面板所需数据主要来源于2006—2018年《中国统计年鉴》《中国环境统计年鉴》《中国科技统计年鉴》以及长江经济带所涵盖的11 个省市的地方统计年鉴，部分缺失数据通过国家统计局官方网站及相关省市官方公布的统计年报进行补充和修正。

选择长江经济带作为本文的研究区域有三点原因：一是自2014 年以来，长江经济带逐渐上升为国家重大战略区域，其经济和社会发展水平整体较高，同时长江上游、中游和下游分别处于我国版图的西部、中部和东部，所涵盖省市在各区域具有典型性和代表性。二是党中央和国务院高度重视长江经济带生态环境保护和治理，习近平总书记分别于2016 年1 月、2018 年4 月、2020 年11 月在长江上游重庆、中游武汉、下游南京等地主持召开推动长江经济带发展座谈会。在这三次会议上，长江经济带“共抓大保护，不搞大开发”的工作总基调十分明确，率先走生态优先、绿色发展的路径要求十分清晰。三是囿于长期粗放的发展方式，长江经济带经济规模不断增加，但流域生态环境系统却不断受到挑战[15]，该区域迫切需要建立起与经济高质量发展相协调的生态环境保护体制机制。

2.1 考虑碳排放的绿色全要素生产率

全要素生产率是宏观经济学的重要概念，是考察衡量经济增长效率的重要依据[16]，相比较而言，绿色全要素生产率在产出方面考虑了非期望产出，即污染排放[17]。长江经济带是工业集聚地，水污染和空气污染尤为严重[18]，因此，本文选择将二氧化碳排放量和化学需氧量作为非期望产出，并在投入中考虑了能源消耗总量，构建生产函数如公式（1）所示：

式中：P为所构建的生产函数，K表示资本投入，即各省市物质资本存量；L表示劳动投入，即各省市三次产业就业总人数；E表示能源消耗，即各省市能源消耗总量；Y表示期望产出，具体用地区生产总值（GDP）指代；U表示非期望产出，具体用各省市二氧化碳排放量和化学需氧量指代。

上述变量中，物质资本存量的测算采用永续盘存法[19]，期初的物质资本存量参考张军等[20]测算的2000年中国各省份物质资本存量，设定折旧率为9.6%。二氧化碳排放量测算参考IPCC[21]计算方法，同时考虑了煤炭、焦炭、汽油、煤油、燃料油、柴油和天然气等7 种化石能源消耗产生的二氧化碳排放量和水泥生产过程中产生的排放量。基于此，构建基于松弛变量的非径向、非角度的SBM模型测算绿色全要素生产率[22]，如公式（2）所示：

式中：gtfpj,t表示j省在t时期的绿色全要素生产率；x、y和u分别代表投入变量、期望产出变量和非期望产出变量；si、sr和sw分别代表投入变量、期望产出变量和非期望产出变量的松弛量；m、s和v分别代表投入变量、期望产出变量和非期望产出变量的个数。

2.2 环境规制强度综合值

本文利用熵值法测算长江经济带各省市环境规制强度的综合值。将工业污染治理完成投资额与工业增加值的比值（er1）、环境污染治理投资额与GDP 的比值（er2）、工业增加值与三废（废水、废气、固废）排放总额的比值（er3）等指标综合考虑。这三种指标均为正向化指标，即指标值越大，说明环境规制强度越强，而环境规制越强说明单位工业增加值的排污量越小，则该地方政府对环境的控制越严格[23]，通过下述公式计算出各指标权重，并得出各省市环境规制强度的综合得分。具体计算过程为：

首先，对三种指标进行无量纲化处理得出Xij，通过归一化避免数据量纲不同对计算结果产生影响，即公式（3）：

其次，用利用熵信息的概念确定各指标权重，即公式（4）：

式中：权重Pij表示第j个属性下第i个指标的贡献度。

然后，用熵值Ej表示所有指标对Xi的贡献总量，如公式（5）所示：

式中：1/lnm为常数，这样保证了0 ≤Ej≤1，当单个指标对于总体的贡献度趋于一致时，Ej趋于1，属性值由所含指标差异大小来决定权系数的大小。

可定义dj为差异系数，即各指标贡献度的一致性程度，则dj=1-Ej，进一步计算出各指标权重Wj，即公式（6）：

最后，根据求得的权重Wj和标准化值Xij计算得出长江经济带11 省市2005—2017 年环境规制强度综合指标值。

3 模型设定与变量描述性分析

3.1 回归模型设定

面 板 向 量 自 回 归 模 型（panel vector autoregression，PVAR）是常用的经济学计量模型之一，其优点是模型将各个变量都视为内生变量，从而分析各个变量及其之后变量对模型中其他变量的影响。可利用面板向量自回归模型检验长江经济带环境规制、技术创新与绿色全要素生产率之间的动态互动关系。因此，本文构建模型如公式（7）所示：

式中：Yit为被解释变量，i表示长江经济带11 个省市；t表示2005—2017 年；Yi,t-p代表Yit的时间滞后项，p为滞后阶数（P=1, 2, 3, …,n），Φp为时间滞后项系数矩阵；μi代表个体固定效应；τt代表时点固定效应；εit代表随机扰动项。将Yit展开得到公式（8）：

式中：Ylngtfp、Ylner和Ylntei分别代表长江经济带各省市绿色全要素生产率、环境规制强度和技术创新水平。

3.2 核心变量描述分析

实证研究的核心变量包括区域环境规制强度综合值（er）、技术创新水平（tei）和绿色全要素生产率（gtfp）。经过数据处理，本文测算得出了长江经济带各省市环境规制综合值以及绿色全要素生产率。

3.2.1 长江经济带环境规制强度综合值

依托长江流域，长江经济带上、中、下游分别地处我国的西部、中部和东部，各区域经济发展和社会条件各不相同，经济社会发展水平大致表现为自西向东逐渐提升的特点，同时，生态环境及自然资源条件也存在差异。根据环境规制强度综合值计算结果，如图1 所示，长江经济带2005—2017 年各地区环境规制强度总体呈“波浪型”上下波动的变化趋势。其中：长江上游地区的环境规制强度在期初相对最高，并保持了较长时间的高强度，变化发生在2014 年，上游地区的环境规制强度不断下降并在2016 年达到最低点（0.128）。长江中游地区的环境规制相对较为平稳，基本处于中等强度。长江下游地区的环境规制强度在2008 年处于最高强度（0.329），自2014 年开始，下游地区环境规制强度超过中上游地区并保持在相对较高的水平。

图1 2005—2017年长江经济带环境规制强度变化趋势

3.2.2 长江经济带绿色全要素生产率

通过构建考虑了非期望产出的生产函数，测算了长江经济带省际绿色全要素生产率，如图2 所示，首先，在研究样本时间期内，长江经济带绿色全要素生产率水平呈现整体下降趋势，但其绿色全要素生产率平均水平（0.487）高于全国（除西藏及港澳台地区以外的30 个省份）的平均水平（0.436）；其次，从长江经济带各地区来看，长江下游地区的整体效率水平最高（0.648），中游地区次之（0.432），上游地区最低（0.368），说明长江经济带绿色生产效率水平存在明显地区差异性，且与我国东中西部地区经济发展水平特征基本一致，呈现“东高西低”的特点。

图2 2005—2017年长江经济带绿色全要素生产率变化趋势

3.2.3 长江经济带技术创新水平

选择长江经济带地区R&D 人员全时当量来指征其技术创新水平，如图3 所示，长江经济带技术创新水平整体呈逐年上升趋势。就其各地区来看，上、中、下游的变化趋势基本具有相同的时间趋势，长江下游地区的技术创新水平最高，中游地区次之，上游地区最低。另外，长江下游地区的技术创新水平与中上游地区相比，二者差距逐年递增，至研究期末，下游地区分别比中上游地区高出20.96 万人和24.58 万人，分别是研究期初的5.9倍和5.2 倍，可见，样本时间期内，长江中游和上游差距变化不大，但下游地区则提升十分显著。

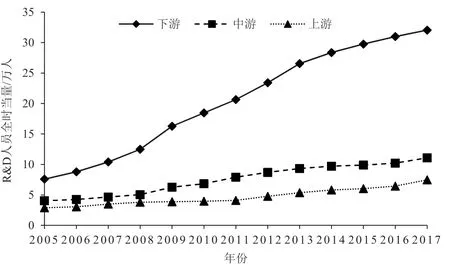
图3 2005—2017年长江经济带技术创新水平变化趋势

3.3 变量描述性统计

实证研究的核心指标和变量的描述性统计结果如表1 所示，为消除模型回归过程中产生异方差的影响，对所有变量采取对数化处理。

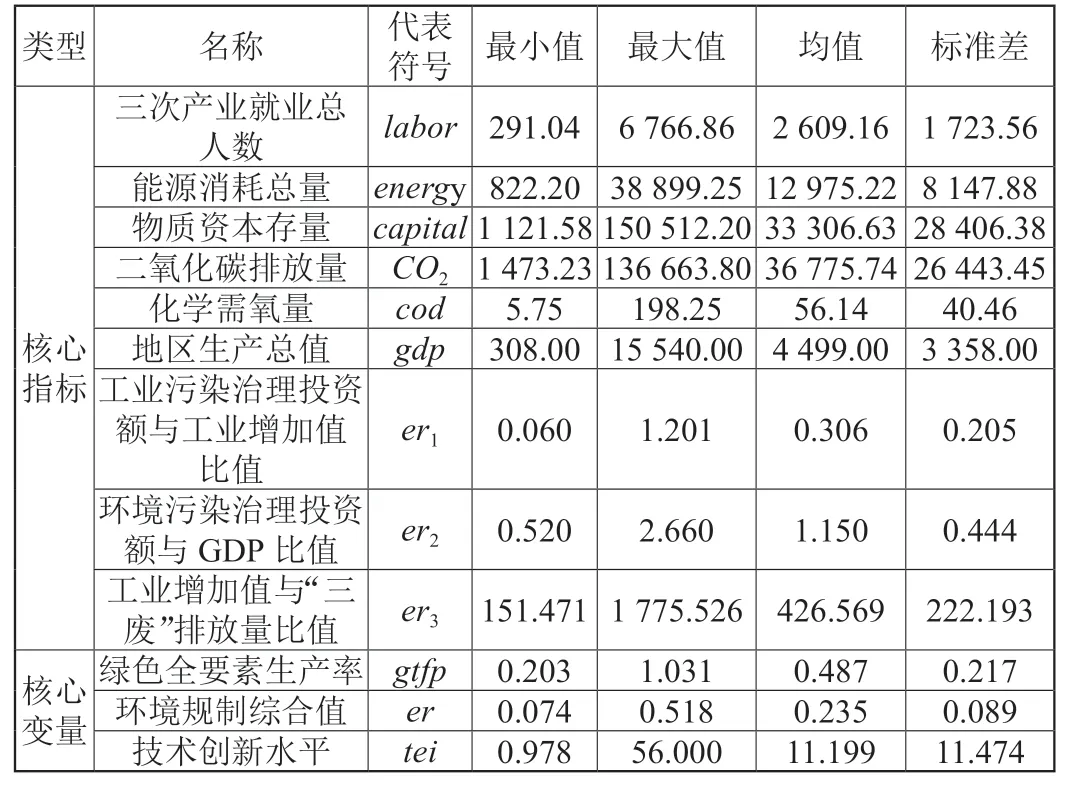
表1 指标和变量描述性统计表（N=143）

4 实证结果与分析

利用上述模型及变量数据对长江经济带区域环境规制、技术创新、绿色全要素生产率之间的关系进行实证检验，进行模型回归前对核心变量进行一阶差分，并对其进行单位根检验和面板协整检验，结果显示三者之间存在长期协整关系。

4.1 模型回归估计结果

利用模型进行回归估计，得到结果如表2 所示，其中，第（1）、（3）、（5）列为一阶面板向量自回归估计结果，作为对比验证，第（2）、（4）、（6）列为普通GMM 模型滞后三阶估计结果。

根据表2 结果，在绿色全要素生产率模型中，长江经济带环境规制强度对地区绿色全要素生产率没有显著影响。技术创新水平对绿色全要素生产率具有显著影响，相关系数在5%的统计水平上显著为-0.240 5，说明在样本研究期内，长江经济带地区技术创新水平提升尚未明显影响地区绿色全要素生产率的变化。在环境规制模型中，长江经济带环境规制强度与绿色全要素生产率之间存在显著关系，二者在5%的统计水平上显著相关，系数为-1.216 3，表明长江经济带整体环境规制强度的增加反而伴随着地区绿色全要素生产率水平的下降。而长江经济带环境规制强度与地区技术创新之间没有显著关系，在技术创新水平模型中，长江经济带环境规制和绿色全要素生产率均对技术创新水平没有解释力，回归系数均不显著。因此，综合来看，长江经济带环境规制与绿色全要素生产率存在动态关系，并且技术创新水平对绿色全要素生产率也存在动态影响，而区域环境规制与技术创新水平在样本研究期内不存在动态关系，二者联系尚不显著。

4.2 最优滞后阶数确定

首 先， 根 据Andrews & Lu[24]提 出 的MMSCaic、MMSCbic和MMSChqic三个信息准则，基于Hansen’s J 统计量信息，用于确定模型回归最优滞后阶数的选取[25]。检验结果显示，MBIC 为一阶最小（-80.416 0），MAIC 为二阶最小（-17.768 8），MQIC 为一阶最小（-42.445 83），综合确定最优阶数为一阶，此时回归估计结果的解释力度最强。再次对模型进行一阶回归估计，所得结果与表2 中第（1）、（3）、（5）列一致。其次，对模型的平稳性进行检验，伴随矩阵特征图显示各点均落在单位为1的同心圆内，即三个特征根均小于1，且都为实根，说明回归模型稳定。

表2 环境规制、技术创新与绿色全要素生产率关系回归结果

4.3 脉冲响应分析

对长江经济带环境规制、技术创新、绿色全要素生产率进行两两Granger 因果关系检验。检验结果显示：长江经济带环境规制与绿色全要素生产率二者影响系数显著，拒绝Granger 检验模型原假设，说明二者互为Granger 因果关系；长江经济带技术创新与绿色全要素生产率二者影响系数均显著，说明二者互为Granger 因果关系；而长江经济带环境规制与技术创新检验结果系数不显著，说明长江经济带环境规制不是技术创新的Granger 因果原因，反之亦然。

在此基础上，利用脉冲响应函数对上述变量之间的相互动态关系做进一步分析，得出变量两两之间的脉冲响应曲线，如图4 所示。其中，第一行图（a）、图（b）和图（c）分别反映以绿色全要素生产率作为脉冲变量，其对自身及技术创新和环境规制变量的响应曲线特征。第二行图（d）、图（e）和图（f）分别反映以技术创新作为脉冲变量，其对自身及环境规制和绿色全要素生产率的响应曲线特征。第三行图（g）、图（h）和图（i）反映以环境规制作为脉冲变量，其对自身及技术创新和绿色全要素生产率的响应曲线特征。

图4 长江经济带环境规制、技术创新与绿色全要素生产率脉冲响应

首先，图（c）和图（g）反映绿色全要素生产率与区域环境规制之间为负向影响，当绿色全要素生产率变高时，区域环境规制强度就降低，在第一期达到曲线最低点，此时影响强度最大，趋向于-0.15，此后随时间逐渐变弱。相对应地，当环境规制强度增加时，地区绿色全要素生产率逐渐下降，影响趋向于-0.02，此后环境规制对绿色全要素生产率的影响逐渐减弱。

其次，图（f）和图（h）反映区域环境规制与技术创新水平的脉冲响应曲线，二者主要为正向影响。技术创新水平对区域环境规制的影响呈倒“U”型，期初影响最大，接近0.15，第5 期以后逐渐趋向于0。区域环境规制对技术创新水平的影响随时间逐渐减弱。

最后，图（b）和图（d）反映技术创新与绿色全要素生产率为负向影响。图（b）中，绿色全要素生产率对技术创新水平的影响在前两期较大，此后逐渐减弱趋向于0。图（d）中，区域技术创新水平对绿色全要素生产率的影响随时间逐渐由-0.02 趋近于0。

4.4 方差分解

为了考察变量之间相互影响的长期动态关系，利用方差分解方法进一步对其进行计量分析。通过方差分解可了解各变量之间相互影响所占的比例，即方差贡献率占比情况，结果如表3 所示，表中重点列出了第1 期、第5 期和第10 期的方差分解结果。

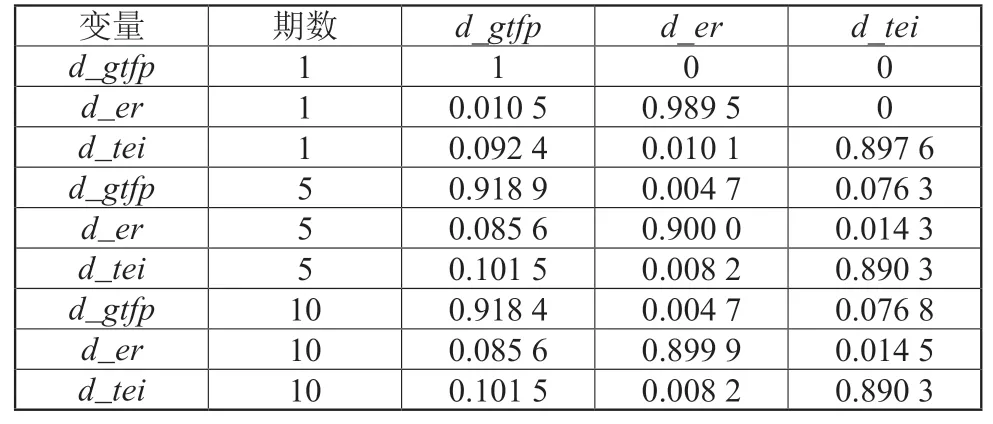
表3 方差分解表

具体而言，第1 期，对长江经济带绿色全要素生产率的影响全部来源于其自身，环境规制的影响主要来源于自身，部分（1.05%）来源于绿色全要素生产率的影响，技术创新的影响主要来源于自身，同时受到绿色全要素生产率（9.24%）和环境规制（1.01%）的影响。至中期（第5 期），长江经济带绿色全要素生产率逐渐受到其他两个变量的影响，0.47%受环境规制变量的影响，7.63%受技术创新变量的影响，环境规制也逐渐受到技术创新变量的影响（1.43%），而绿色全要素生产率变量对环境规制的影响提升了7.15 倍，达到8.59%，技术创新受其他两个变量的影响变化不大，受自身影响比重是89.03%，受环境规制影响比重为0.82%，受绿色全要素生产率影响比重为10.15%。末期，即第10 期，各变量的方差分解结果与中期结果大致相似，各部分影响比例变化不大。通过上述方差分解结果可以看出，长江经济带环境规制、技术创新和绿色全要素生产率三者之间的动态互动关系在中期至末期达到较为稳定的影响关系，说明三者之间互动关系逐渐密切。

4.5 稳健性检验

通过变换技术创新水平的指标，对模型稳健性进行检验，分别用地区R&D 内部经费支出与地区生产总值的比值（tei1）和地区专利授权数指标（tei2）对原模型技术创新变量进行替换，得出回归估计结果如表4 所示。替换变量后的模型通过了单位根检验、协整检验和模型稳定性检验，回归估计结果、脉冲响应和方差分解与原模型回归结果基本一致。

表4 稳定性检验结果

5 研究结论与启示

生态环境保护与经济的高质量发展是推进区域协调发展的重要研究课题，长江经济带迫切需要在“共抓大保护、不搞大开发”的环境保护总基调下，实现经济的高质量发展。因此，研究环境规制、技术进步与绿色全要素生产率之间的关系具有重要的理论及现实意义。通过构建长江经济带2005—2017 年动态平衡面板数据，利用面板向量自回归模型，本文定量检验了长江经济带环境规制、技术创新与绿色全要素生产率之间的动态互动关系，基于上述实证研究，结论如下：（1）长江经济带环境规制与绿色全要素生产率存在显著的动态互动关系，相关系数在5%的统计水平上显著为-1.216 3，而长江经济带绿色全要素生产率与技术创新也存在显著的动态互动关系，其系数在5%的统计水平上显著为-0.240 5，同时，检验结果显示，长江经济带环境规制的强弱尚未对技术创新产生显著影响，研究样本期内，二者不存在动态互动关系。（2）整体上，通过脉冲响应特征曲线来看，长江经济带环境规制、技术创新和绿色全要素生产率之间存在长期动态影响关系。其中，环境规制与绿色全要素生产率之间呈现负向显著影响，说明长江经济带环境规制强度的提升反而伴随着区域绿色全要素生产率的下降，而绿色全要素生产率的提升则伴随着环境规制强度的减弱。就技术创新的动态效应来看，长江经济带技术创新水平的提升并没有相应地提升长江经济带绿色全要素生产率，二者影响随时间而逐渐减弱。另外，长江经济带环境规制与技术创新之间的动态互动关系尚不显著，样本期内，二者尚不能说明“波特假说”成立。（3）根据方差分解结果，长江经济带环境规制、技术创新和绿色全要素生产率之间影响在第5 期至第10 期逐渐趋于稳定，整体上，环境规制对绿色全要素生产率的贡献度为0.47%，技术创新对绿色全要素生产率的贡献度为7.68%，技术创新对环境规制的贡献度为1.45%。根据上述研究所得结论，得到以下启示：一是区域环境规制能否促进技术创新应充分考虑经济社会发展条件的不同阶段和地区差异。就长江经济带而言，通过上述实证研究显示二者影响关系尚不显著。因此，长江经济带在坚持绿色高质量发展的同时，应提升集经济建设、政治建设、文化建设、社会建设、生态文明建设于一体的改革，以进一步培育适宜于绿色技术创新的“制度土壤”。

二是区域环境规制对地方经济社会发展至关重要，由于生态环境具有公共外部性，在促进市场化改革中，政府应始终坚持主导作用。在《长江保护法》的法律保障下，长江经济带战略兼具发展经济和保护环境的双重任务。因此，在鼓励多元化政策工具的同时，应重点解决不同区域的“因地施策”。

三是区域绿色全要素生产率的提升是经济高质量发展的内在要求。在促进企业绿色技术创新的同时，政府应继续深化要素市场化改革的深度和广度，使企业在投入与产出之间取得综合效益最大化，更具面向国际市场的竞争力，这也是“波特假说”的内在逻辑。因此，长江经济带作为重大战略区域，在市场化改革方面具有政策优势，应加快区域市场一体化建设，努力构建国际国内双循环新发展格局，加快建成高质量发展的“黄金经济带”。