伴随敏感性方法、第一奇异向量方法以及条件非线性最优扰动方法在台风目标观测敏感区识别中的比较研究

周菲凡 叶一苇 段晚锁 张贺

1 中国科学院大气物理研究所云降水物理与强风暴重点实验室, 北京 100029

2 中国科学院大学, 北京 100049

3 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室, 北京 100029

4 中国科学院大气物理研究所国际气候与环境科学中心, 北京 100029

5 南京信息工程大学气象灾害预报预警与评估协同创新中心, 南京 210044

1 引言

许多资料同化和可预报性研究（Reynolds et al., 1994; Rabier et al., 1996; Simmons and Hollingsworth, 2002; Froude et al., 2007）表明，预报误差的主要部分通常来自于初始场的不确定性，因此对初始态的准确估计为提高预报技巧提供了有效的途径（Simmons, 1995）。而要提供更准确的初始场，方法之一是增加额外的观测。然而，由于观测资料的有效利用取决于具体的天气过程，人们开始由简单地增加观测的时空分辨率与空间覆盖率的观测策略向重点加强关键地区观测的策略转变，这就是适应性观测（Snyder, 1996），又称目标观测。

具体地，目标观测是指为了提高未来某一特定时刻（验证时刻）、特定区域（验证区域）可能发生的天气过程的预报质量，在此之前的某一时刻（目标观测时刻）、某一区域（目标观测区域或敏感区）实施加强观测。目标观测自从被提出以来已经被用于锋面和大西洋风暴追踪试验FASTEX（Joly et al., 1997）、北太平洋试验NORPEX（Langland et al., 1999）、冬季风暴观测试验WSR（Szunyogh et al., 2002）以及我国台湾地区开展的热带气旋监视计划（DOTSTAR）（Wu et al., 2005,2007）。上述外场观测试验结果表明，平均而言，目标观测提高了预报技巧（Bergot, 1999, Bergot et al., 1999; Szunyogh et al., 2002; Wu et al., 2005）。

目标观测的关键在于敏感区（目标观测区域）的识别，这直接影响了目标观测的有效性。目前，常见的敏感区识别方法主要可以分为两类，一类是从误差增长的动力学角度出发，通过识别快速增长的初始误差或者求取目标函数关于初始条件的梯度信息，进而识别敏感区，例如，第一奇异向量方法（LSV，Palmer et al., 1998）、条件非线性最优扰动方法（CNOP，Mu et al., 2009）、繁殖向量方法（BV, Toth and Kalnay, 1997）、以及伴随敏感性方法（ADS，adjoint sensitivity）（Baker and Daley,2000; Kim et al., 2004; Ancell and Mass, 2006），另外，还有基于伴随梯度技术的ADSSV 方法（Wu et al., 2007）和DLM 方法（Aberson, 2003），后两种方法实际上是伴随敏感性方法的拓展。另一类方法是与资料同化相结合的方法，也即通过比较同化不同区域的观测资料对预报技巧的改善程度，将对预报技巧改善较大的资料区域作为目标观测区域，例如，集合转换方法（ET）、集合卡曼滤波方法（EnKF, Hamill and Snyder, 2002）、集合转换卡曼滤波方法（ETKF, Bishop et al., 2001）、三维变分同化—观测系统模拟试验方法（3DVAR-OSSE，Huang and Meng, 2014）。研究表明，以上各种方法确定的敏感区各不相同，而且同一方法在不同试验过程中改善预报效果的程度也不同（Palmer et al., 1998; Hamill et al., 2000; Majumdar et al., 2006）。毋庸置疑每种方法都有其优缺点。对于资料同化类的方法，由于在观测之前我们就需要进行敏感区的识别，因此，只能是同化假想的观测资料，这必然会导致最终识别的敏感区有误差。在资料同化类方法中，大部分都采用了集合的技术，而集合样本数及其代表性也会影响敏感区的识别，再者，如果深入挖掘采用集合技术的方法识别敏感区的原理，可以发现这类方法事实上是线性方法。而在误差增长动力学类方法中，LSV 和ADS 方法及其拓展的方法都是线性的，BV 虽然是非线性的，但是由于其缺乏理论基础，是一种经验性的推断。CNOP 也是非线性的方法，在理论上具有较大的优势，然而其计算代价较高，当采用较高分辨率（比如30 km 以下）时，以当前的超级计算机的性能，很难满足业务的时效性需求。可见，每种方法都有其优缺点，具体在目标观测中采用哪种方法识别敏感区要根据实际情况和要求而选取。

由于LSV 和ADS 方法都是线性的方法，并且其理论基础考虑的也都是误差的动力学增长，那么这两种方法具体在识别敏感区的原理上有何区别？识别的敏感区又有多大的异同？它们识别的敏感区的有效性怎么样？同时又由于LSV 可以看成是CNOP 的线性近似，那么在不同的非线性程度下，LSV、ADS 和CNOP 识别的敏感区会有多大的不同？针对上述问题，本文将首先深入分析伴随敏感性方法、第一奇异向量方法、以及条件非线性最优扰动方法在目标观测敏感区识别方面的原理，接着以两种在移动路径方面有对比性的台风个例作为研究对象，探讨两种不同路径的台风的非线性程度，在此基础上，考察LSV、ADS 和CNOP 识别的敏感区的异同及有效性，进而综合评判三种方法用于目标观测外场试验的有效性。

2 方法介绍

2.1 伴随敏感性（ADS）方法

所谓伴随敏感性方法，即借助伴随模式求取目标函数对初始时刻变量场的梯度，用该梯度进行相关研究的方法（董佩明和张昕, 2004; Kim et al.,2004; Ancell and Mass, 2006）。在目标观测中，求得的梯度场可以用来确定目标观测的敏感区（通常取梯度值大于某一量值的区域）。

2.2 第一奇异向量（LSV）方法

可见，第一奇异向量可以表示在有限时段内具有最大增长率的初始误差。在目标观测中，我们力求通过增加观测减小这种快速增长的初始误差，进而提高预报技巧。这里值得注意的是，奇异向量表征的误差增长是线性增长，因此，它同伴随敏感性方法一样，具有线性局限性，在具有较强非线性过程的事件中，该方法就难以识别出准确的敏感区。

从伴随敏感性方法和奇异向量方法的定义可以看出，这两种方法都是线性的方法，在线性近似成立的前提下，它们的区别在于伴随敏感性方法得到的敏感性表示的是每一变量对预报状态的一个最大的影响，变量之间彼此是独立的。而从公式（9）可以看出，线性奇异向量考察的是不同变量作为一个整体对预报状态的最大影响，变量之间在某种特定的组合下对预报的影响最大。而变量的某种特定的组合是由切线性模式所决定。这里需要指出的是切线性模式L不能脱离基本态而存在，事实上切线性模式L由非线性模式M和初始分析场x0共同决定，因此，变量的某种特定的组合由非线性模式M和初始分析场x0共 同决定，而与初始误差δx0无关。同样地，伴随敏感性方法中，伴随敏感性梯度也由非线性模式M和初始分析场x0共同决定，与初始误差 δx0无关。但是，两种方法都与目标函数的定义，也即度量范数G有关。

2.3 条件非线性最优扰动（CNOP）方法

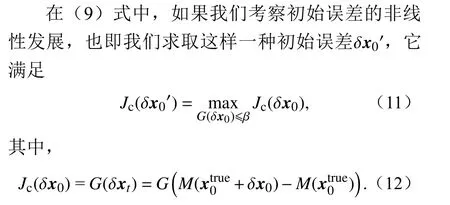
我们把这样的一种初始误差称为条件非线性最优扰动（穆穆等, 2007）。可见，CNOP 是LSV 在非线性空间的拓展，它可以克服LSV 的线性局限性，进而寻找出在非线性空间对预报影响最大的初始误差。同样地，我们可以通过消除初始场中这样的一种初始误差，进而提高预报技巧。

联合（11）式，CNOP 可以这么理解：当初始分析场x0具 有CNOP 型初始误差时，基于分析场x0的预报将具有最大的预报误差。为避免这种最糟糕的预报发生，我们应尽量使初始分析场中最大可能地不具备CNOP 型初始误差。因此，CNOP 方法应用于目标观测时，我们取CNOP 型初始误差的大值区作为目标观测的敏感区，在该区域增加观测，减小误差，可以最大程度地减小CNOP 型误差，从而使得初始分析误差最大程度地不具备有CNOP形态。上述即为CNOP 方法应用于目标观测敏感区识别的主要原理。周菲凡和张贺（2014）详细地阐述了如何具体地利用求得的CNOP 型初始误差确定敏感区，并且得到“垂直积分能量方案”为最优方案。简单地讲，该方案综合考虑了CNOP 型初始误差各个变量场的大值区，通过求取CNOP型初始误差能量的水平分布，将能量大值区做为目标观测的敏感区。由于LSV 即为CNOP 的线性近似，因此，LSV 方法和CNOP 方法识别敏感区的原理以及具体如何确定敏感区类似。

2.4 非线性程度计算

既然LSV 是CNOP 的线性近似，那么如果二者比较相似，则说明该事件可以用线性近似描述，因此该事件的非线性比较弱；反之，如果二者差别比较大，则说明该事件不能用线性近似描述，该事件的非线性比较强。因此我们可以通过计算CNOP 和LSV 的相似程度来判断一个事件的非线性程度。

我们采用如下公式计算两个向量之间的相似系数（S）：

其中，S为CNOP 和LSV 的相似系数。可见，Nd值越大，非线性越强，反之，非线性越弱。

3 试验设计

3.1 研究对象

如引言所述，本文选取了两种在移动路径方面有对比性的台风个例进行研究，一组是研究时段路径发生转折的台风，一组是研究时段无转折的台风，且选用研究时段的终止时刻为验证时刻，初始时刻为目标观测时刻。研究台风个例如表1 所示。我们根据2.4 节介绍的非线性程度的计算方法计算每个台风个例的非线性程度。可见，转向型台风的非线性程度差别比较大，有的非线性特别强，有的非线性特别弱，而直线型个例非线性程度则相对比较一致。此外，对于非线性较强（非线性程度数值大于6）的4 个个例，可以发现，它们或处于强台风时期，或处于快速发展加强时期。不过需要指出的是并不是强台风非线性就强，比如2010Megi_1 台风，其属于强台风，但是非线性程度较弱。可见，台风的强度与非线性程度没有必然的联系。

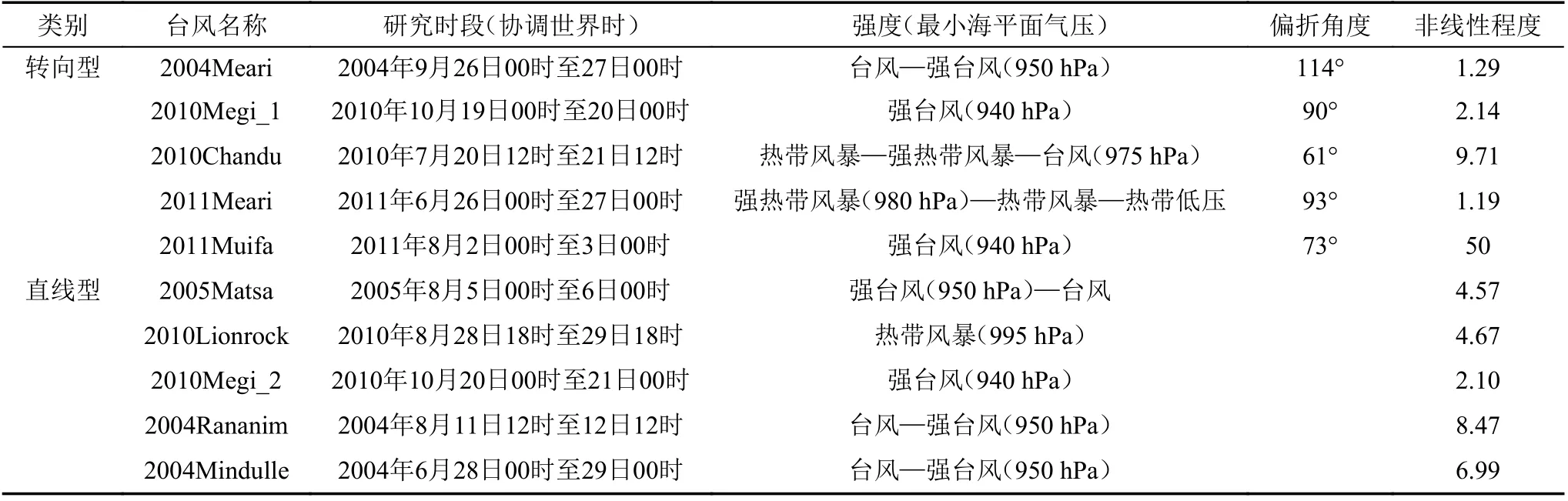
表1 台风类型、名称及其对应的研究时段、强度、偏折角度和非线性程度Table 1 The types, names of the typhoons and the studied period for each typhoon with the corresponding strength, recurved degree, and the nonlinear degree

3.2 模式、资料简介

本文所使用的模式是宾西法尼亚大学和美国国家大气研究中心（PSU-NCAR）共同开发的中尺度模式MM5（Dudhia, 1993）及其对应的切线性和伴随模式系统（Zou et al., 1997）。采用的参数化方案主要有：干物理过程、大尺度降水、Anthes-Kuo 积云对流参数化和高分辨率边界层参数化。使用的资料为美国国家环境预测中心（NCEP）发布的全球业务（1°×1°）最后分析资料（简称FNL）。由该资料插值到MM5 模式格点上形成初边值条件。分辨率取60 km，水平格点数除了2004Meari 为51×55， 其 余 均 为55×55； 垂 直 层 数 除 了2004Meari 和2005Matsa 为11 层，其余均为20 层，模式层顶都为100 hPa。

3.3 度量范数

本文的度量范数G取定义在验证区域上的干能量范数，虽然干能量不能直接体现出台风路径的变化情况，但是可以通过风场、温度场和气压场间接地给出一定的信息。在干能量范数度量下目标函数J1、Js、Jc可以分别表示为

3.4 敏感性区域的确定

对于伴随敏感性方法，为便于比较，我们将求得的梯度标准化，记目标函数J1对初始分析场x0的梯度为g1。事实上，g1由J1对初始纬向风、经向风、温度场以及气压场等的梯度组成。在本文中，我们将J1对初始纬向风场的梯度和对初始经向风场的梯度结合起来做为一个矢量进行分析，简称为矢量风梯度场；称J1对初始温度场的梯度为温度梯度场；同样地，称J1对初始气压场的梯度为气压梯度场。由于在所研究的个例中，当温度梯度和气压梯度的绝对值大于3，矢量风梯度值大于4 时，梯度场呈现出较为明显的局地特征，因此在本研究中我们将标准化后的温度梯度以及气压梯度绝对值大于3、矢量风梯度值大于4 的区域作为伴随敏感性方法识别的对应各个变量的目标观测敏感区。

周菲凡和张贺（2014）将CNOP 或者LSV 的垂直积分能量的大值区作为敏感区，这里为了便于与伴随敏感性方法进行比较，我们分别考察CNOP和SV 的各个变量场的分布，结果发现，当风场大于0.3 m/s、温度场绝对值大于0.2 K、气压场绝对值大于0.3 hPa 时，各个变量场的分布具有局地性的特征，且多数个例在这个阈值下得到的大值区大小与伴随敏感性方法得到的敏感区大小相当。因此，我们将各个变量场满足上述阈值的大值区作为各变量场的敏感区。然后将各个变量的敏感区与伴随敏感性方法得到的各个变量的敏感区进行比较。

4 数值结果与分析

4.1 敏感区的比较

4.1.1 不同非线性程度下各方法识别的敏感区的差异

首先，我们考察非线性较弱的个例。图2 分别给 出 了2004Meari、2011Meari、2010Megi_2 的 伴随敏感性（图2a、d、g）、线性奇异向量（图2b、e、h）以及条件非线性最优扰动（图2c、f、i）在σ=0.7层（约800 hPa）上的温度和风场的敏感区的分布。可见，在非线性较弱的情况下，CNOP和LSV 识别的敏感区是十分相似的。这说明了LSV 是CNOP 的线性近似，在非线性较弱，也即线性近似可以成立的时候，采用LSV 识别敏感区与采用CNOP 识别敏感区基本一致，此时可以用LSV 近似替代CNOP。此外，ADS 方法识别的敏感区与CNOP 和LSV 的敏感区也有一定的相似性，但是相似度不如CNOP 敏感区和LSV 敏感区的相似度。由前方法介绍中我们知道，ADS 方法主要考虑的是在线性发展的情况下每一变量对预报状态的一个最大的影响，变量之间彼此是独立的。而线性奇异向量考察的是在线性发展的情况下不同变量作为一个整体对预报状态的最大影响。所以二者识别的敏感区是有可能不一样的。现在由我们的结果可以看出，全局考虑所有变量与单独考虑各个变量的敏感性时，敏感区的分布形势的确会有所不同。这也意味着在目标观测中同时对所有变量进行观测和单独对某个变量进行观测，观测的位置则有可能不同。

图1 目标函数J1 对初始分析场x0 的梯度的求解过程示意图Fig. 1 Schematic diagram of the solving process for the gradient of the cost function (J1), with respect to the initial analysis (x0). M indicates the nonlinear model, and G is the measurement of the forecasts (xt), L* is the adjoint model of L, which is the tangent model of M

图2 （a-c）2004Meari、（d-f）2011Meari、（g-i）2010Megi_2 台风， σ=0.7 层ADS 方法（上）、LSV 方法（中）、CNOP 方法（下）识别的风场（箭头）、温度场（彩色阴影）敏感区以及各台风研究时段起始时刻的500 hPa 位势高度场（等值线，等值线间隔20 gpm）。上行图中，箭头表示矢量风梯度，只绘制了值≥4 m s-1 的区域；彩色阴影表示温度梯度，只绘制了绝对值≥3 J kg-1 K-1 的区域。中、下行图中，箭头表示风场，只绘制了值≥0.3 m s-1 的区域；彩色阴影表示温度场，只绘制了绝对值≥0.2 K 的区域。长方形区域为验证区域，圆圈和加号表示研究时段初始时刻台风中心所处的位置Fig. 2 The sensitive areas of wind (arrows) and temperature (color shadings) identified by ADS (adjoint sensitivity, top panels) method, LSV (leading singular vector, middle panels) method, CNOP (conditional nonlinear optimal perturbation, bottom panels) method at the level of σ=0.7 for (a-c)typhoon 2004Meari; (d-f) typhoon 2011Meari; (g-i) typhoon 2010Megi_2. In top panels, arrows represent the gradients with respect to wind whose values are larger than 4 m s-1 are plotted, color shadings represent the gradient with respect to temperature whose absolute values are larger than 3 J kg-1 K-1 are plotted. In middle and bottom panels, arrows represent wind whose value is larger than 0.3 m s-1 are plotted, color shadings represent temperature whose absolute value is larger than 0.2 K are plotted. The rectangles indicate the targeted area, and the circle and cross symbols indicate the initial position of the typhoon

而当非线性较强时，例如2011Muifa，可以看到，此时CNOP 和LSV 识别的敏感区差别较大（图3b、c），但是此时伴随敏感性方法识别的敏感区（图3a）则与LSV 识别的敏感区（图3b）较为相似。从表1 可知2011Muifa 具有非常强的非线性，非线性强度比2011Muifa 弱的中等非线性强度的台风，比如2004Mindulle 和2005Matsa，也具有类似的特征，也即CNOP 和LSV 识别的敏感区差别较大（图3e、f、h、i），但是此时ADS 方法识别的敏感区（图3d、g）则与LSV 识别的敏感区（图3e、h）较为相似。可见，当台风具有一定的非线性强度时，LSV 方法识别的敏感区与CNOP方法识别的敏感区有较大差异。而此时，两种线性方法之间识别的敏感区的差异则变得很小。这很有可能是因为当线性方法与非线性方法的异同扩大时，线性方法之间的异同就缩小了。综合可见，当非线性较弱时，LSV 方法识别的敏感区倾向于与CNOP方法识别的敏感区一致，而当非线性较强时，LSV方法识别的敏感区则倾向于与伴随敏感性方法一致。事实上，当非线性较强时，线性方法识别的敏感区的准确性就降低，我们将在4.2 节中敏感区的有效性中进行详细的分析。

图3 同图2，但为（a-c）2011Muifa、（d-f）2004Mindulle 和（g-i）2005Matsa 的敏感区及各台风研究时段起始时刻的500 hPa 位势高度场Fig. 3 As in Fig. 2, but for the sensitive areas of (a-c) 2011 Muifa, (d-f) 2004 Mindulle, and (g-i) 2005 Matsa and 500-hPa geopotential height at the beginning of the study period for each typhoon

从图2、3 可以看出，不论非线性强还是弱的个例，三种方法识别的敏感区都主要位于台风和副热带高压（简称副高）交界的地方。对于非线性较弱的个例，敏感区更多地位于交界处偏向副高的一侧，体现了副高对台风的显著影响；而对于非线性较强的个例，敏感区更多地位于交界处偏向台风的一侧，体现了台风自身热动力结构对台风行进的影响。不论非线性强还是弱的个例，非线性方法既能识别出台风与副高交界处的区域，又能识别出台风外围螺旋结构对台风的影响。

4.1.2 转向与非转向台风敏感区的差异

大气的发展运动是非线性的过程，台风的生成、发生、发展过程显然也是非线性的，即便一些台风的发展过程非线性较弱，但也不能否认它的非线性性。显然，用非线性方法识别的敏感区也肯定要比用线性方法识别的敏感区更为准确，在前人的众多研究中也说明了这一点（Zhou and Mu, 2011; Qin and Mu, 2011; Chen and Mu, 2012; 周菲凡和张贺,2014）。因此，这里我们考虑转向与非转向台风的敏感区差异时，主要考虑CNOP 方法识别的敏感区在两种类型台风中的差异。图4 给出的是转向型的台风，这些台风在研究时段内发生了较大的转折，我们发现这一类台风敏感区的共同点是都主要位于台风行进路径的右前方（图4），也即初始台风中心位置的东北象限区域。而对于非转向型台风，这些台风在研究时段内行进方向一致，我们发现对于这一类台风，敏感区更多是位于台风行进路径的右后方或者正后方（图5），也即初始台风中心位置的东南或西南象限区域。转向型台风和非转向型台风的敏感区的分布差异表明对于转向型台风，其行进前方会出现重要的阻拦或干预，而对于非转向型台风其前行路上受到的影响较小。这里给我们的启示是我们是否可以通过台风与其敏感区的相对位置来判断其前行的方向？是否当求得的敏感区位于当前台风行进路径前方时预示着台风将会发生转折，而当敏感区位于台风“身后”时预示着台风将继续前进？当然，这些都有待于对多种移动类型的台风进行系统的、大量的数值试验以及深入的物理分析。

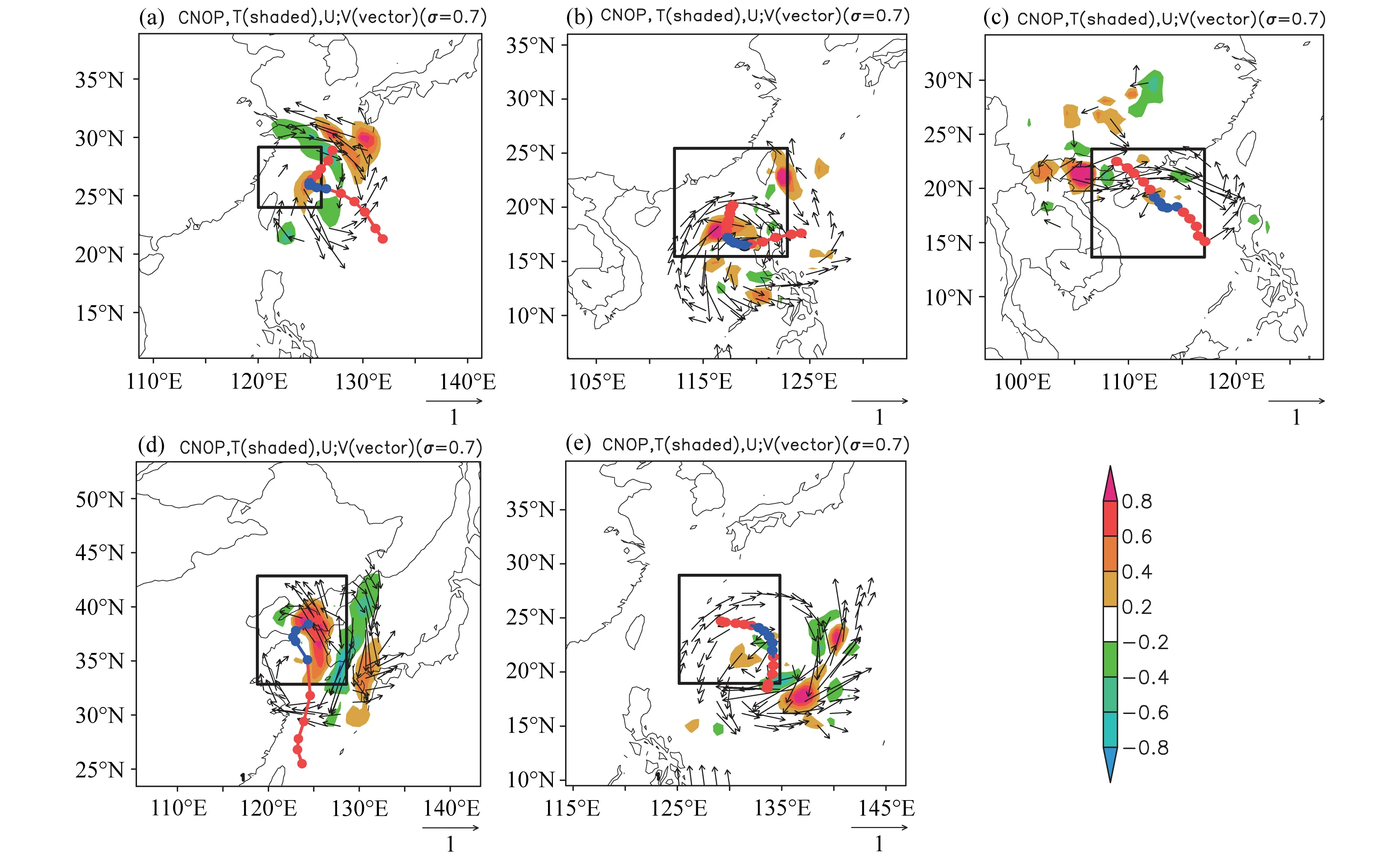
图4 （a）2004Meari、（b）2010Megi_1、（c）2010Chandu、（d）2011Meari、（e）2011Muifa 台风在研究时段的行进路径（蓝色线段）以及研究时段前、后各24 h 的行进路径（红色线段）以及CNOP 方法识别的 σ=0.7 层的风场和温度场的敏感区Fig. 4 Tracks of (a) 2004 Meari, (b) 2010 Megi_1, (c) 2010 Chandu, (d) 2011 Meari, and (e) 2011 Muifa during the study period (blue lines), 24 h before and after the study period (red lines), and the sensitive areas of wind (vectors, units: m/s) and temperature (shadings, units: K) identified by the CNOP method

图5 同图4，但为（a）2005Matsa、（b）2010Lionrock、（c）2010Megi_2、（d）2004Rananim、（e）2004Mindulle 行进路径及风场、温度场的敏感区Fig. 5 As in Fig. 4, but for tracks of (a) 2005 Matsa, (b) 2010 Lionrock, (c) 2010 Megi_2, (d) 2004 Rananim, (e) 2004 Mindulle, and sensitive areas of wind and temperature

4.2 敏感区的有效性分析

前人的许多研究已经表明CNOP 方法识别的敏感区比LSV 方法识别的敏感区更为有效（Zhou and Mu, 2012a, 2012b; Chen et al., 2013）， 在CNOP 方法识别的敏感区内增加观测可以更大程度地提高预报技巧，换言之，预报对CNOP 方法识别的敏感区内的初值更加敏感，也即在CNOP 方法识别的敏感区内的初始扰动增长更快，对预报的影响更大。那么这里我们重点考察的是在不同非线性程度、以及转向与非转向台风中，三种方法识别的敏感区的有效性或者说预报对初值的敏感性程度会不会有所差别？如果有，差别有多大？由图2 和图3 我们可以看出，不同方法识别出的敏感区大小是不一样的，为了使得敏感性试验更为公平，这里我们对所有方法识别的敏感区取相同的大小。我们参照周菲凡和张贺（2014）中介绍的“垂直积分能量方案”，首先计算CNOP、LSV 和ADS 的垂直积分能量，将垂直积分能量从大到小排序，取前20 个大值所在的格点作为敏感区。由周菲凡和张贺（2014）的图2c 与图1a，图3c 与图1b 可以看出，该方式确定的敏感区能够抓住本文中图2～5所呈现的主要敏感区，在保证各方法确定的敏感区具有相同大小的情况下，又能抓住最敏感的区域。接着，我们在敏感区所在的整层大气内分别对风场、温度场和气压场产生均值为0，风场的方差为1.414 （m s-1）2，温度场方差为0.7328 K2，气压场方差为5 hPa2，且满足正态分布的随机扰动，并进一步将随机扰动约束到0.03 J/kg，以确保随机扰动具有相同的振幅。接着，我们将随机扰动叠加到初始基态场上，考察随机扰动的非线性发展情况。

图6 给出了非线性最弱的2011Meari 和非线性最强的2011Muifa 个例不同方法识别的敏感区内随机扰动的非线性发展情况。由图可见，在CNOP敏感区内叠加的随机扰动，不论是强非线性台风还是弱非线性台风，其发展都是最大的，而LSV 敏感区内叠加的随机扰动发展次之，ADS 方法识别的敏感区内叠加的扰动发展最小。此外，我们还可以看到，在非线性较强（2011Muifa）的个例中，CNOP 敏感区的有效性要远远大于LSV 和ADS 方法识别的敏感区的有效性，而在非线性较弱（2011Meari）的个例中，CNOP 敏感区的有效性虽然也依然位于第一位，但是和LSV 敏感区、ADS敏感区的有效性相差不大。进一步，我们分析了不同方法识别的敏感区内叠加随机初始扰动非线性发展后导致的海平面气压的变化，依然以2011Meari和2011Muifa 为例。由图7 可见，在非线性较弱的2011Meari 个例中，三种方法识别的敏感区内的扰动非线性发展后都使得验证区域内的海平面气压发生了较大的的变化，意味着初始扰动对预报终止时刻的台风的强度和路径都产生了较大的影响。扰动使得终止时刻台风中心位置气压升高，台风变弱，同时由于它还使得验证区域内其他区域气压降低，因此使得终止时刻预报的台风中心位置发生了偏移（图7）。此外，CNOP 方法和LSV 方法识别的敏感区内扰动发展对海平面气压的影响较为相似（图7b、c），这和二者的敏感区较为相似互相呼应，ADS 方法识别的敏感区和另外两种方法识别的敏感区差别较大（图2d-f），因此在ADS 方法识别的敏感区内叠加扰动对预报的影响也和另外两种方法识别的敏感区内扰动发展对预报的影响不同。而在非线性较强的个例2011Muifa 中，ADS 方法和LSV 方法由于其识别的敏感区较为相似，因此扰动发展后对海平面气压的影响也较为相似（图7d、e），但是明显小于CNOP 方法识别的敏感区内的扰动发展的影响，可以看见，CNOP 方法识别的敏感区内的扰动发展后对验证区域内的海平面气压产生了大范围大幅度的影响，使得台风中心位置发生了相对明显的偏离（图7f）。总的来说，不论哪种类型台风，CNOP 方法识别的敏感区内的扰动发展都对台风影响最大。

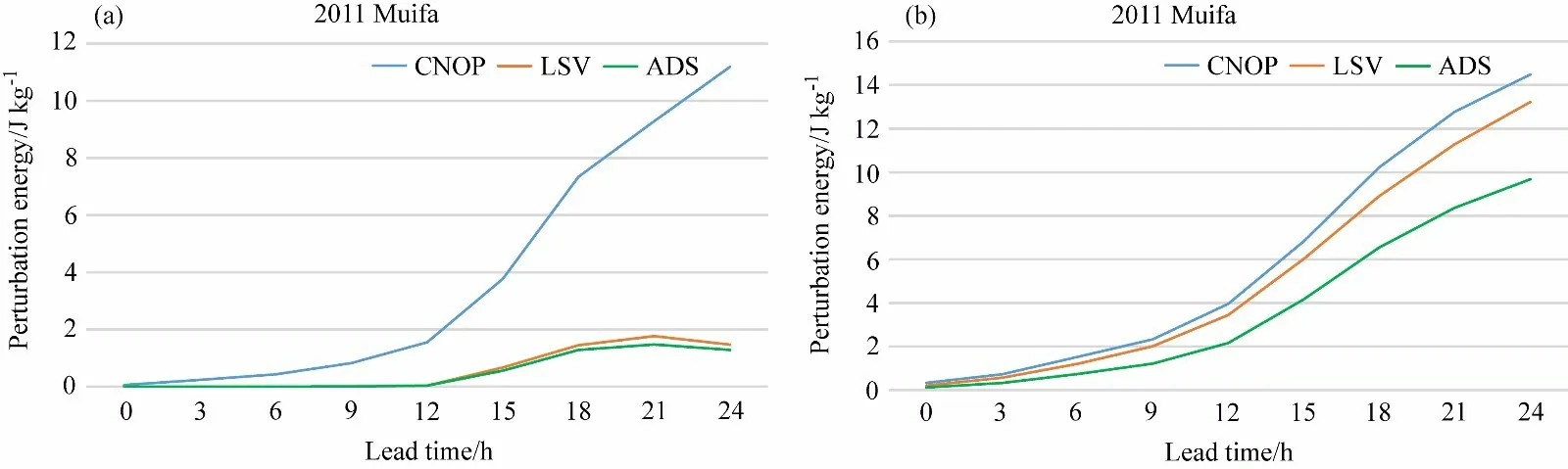
图6 CNOP、LSV、ADS 识别的敏感区内随机扰动能量随预报时间的变化：（a）2011Meari；（b）2011MuifaFig. 6 Energy development of the random perturbations added in the CNOP-, LSV-, and ADS-identified sensitive areas with lead time: (a) 2011 Meari; (b) 2011 Muifa

图7 （a-c）2011Meari、（d-f）2011Muifa，在（a、d）ADS、（b、e）LSV、（c、f）CNOP 方法识别的敏感区内叠加随机初始扰动导致的海平面气压变化（彩色阴影，单位：Pa）以及研究时段终止时刻分析资料的500 hPa 位势高度场（等值线，单位：gpm，等值线间隔20 gpm）。长方形区域为验证区域，圆圈和加号符号表示研究时段终止时刻未叠加扰动预报的台风中心所处的位置，黑色三角形符号表示叠加随机初始扰动后预报终止时刻台风中心所处的位置Fig. 7 Variations of the sea level pressures (shadings, units: Pa) caused by the random initial perturbations added in the sensitive areas identified by the (a, d) ADS, (b, e) LSV, and (c, f) CNOP methods, and 500-hPa geopotential height (contours, units: gpm, contours interval: 20 gpm) at the end of the study time period from the analytical data for (a-c) typhoon 2011 Meari and (d-f) typhoon 2011 Muifa. The rectangles indicate the targeted area,the circle and cross symbols indicate the final position of the typhoon from control forecasts (without perturbations), and the solid triangle indicates the final position of the typhoon from the forecasts with perturbations

我们根据表1 中的非线性程度将台风分为两组，一组非线性程度数值小于4，称为弱非线性组，这一组一共4 个台风个例，将剩下的6 个台风归为强非线性组。接着我们比较同一方法识别的敏感区在不同非线性程度下的有效性，我们分别考察每一组中敏感区内扰动的平均发展情况。由图8a 可见，不论是CNOP 敏感区，还是LSV 敏感区，或是ADS 敏感区，弱非线性组中扰动的发展明显要大于强非线性组中扰动的发展，这也就意味着对于非线性较弱的个例，其预报受初值的影响更大，因此目标观测效果可能会更明显。接着，我们把转向型台风分为一组，直线型台风分为一组，考察同一方法识别的敏感区在转向型和直线型台风中的有效性。由图8b 可见，对于CNOP 敏感区，直线型台风扰动发展大于转向型台风，而对于LSV 和ADS 敏感区，扰动在两种台风类型中发展相当，但是都明显小于CNOP 敏感区中的随机扰动的发展，这说明CNOP 敏感区最为有效。又由于平均而言直线型台风CNOP 敏感区内的扰动发展较转向型台风发展要大一些，而LSV 敏感区和ADS 敏感区内扰动在直线型和转向型台风中的发展是相当的，因此，预报对初值的敏感性在转向型台风和直线型台风中的差异会因初始场所在的区域的不同而不同。

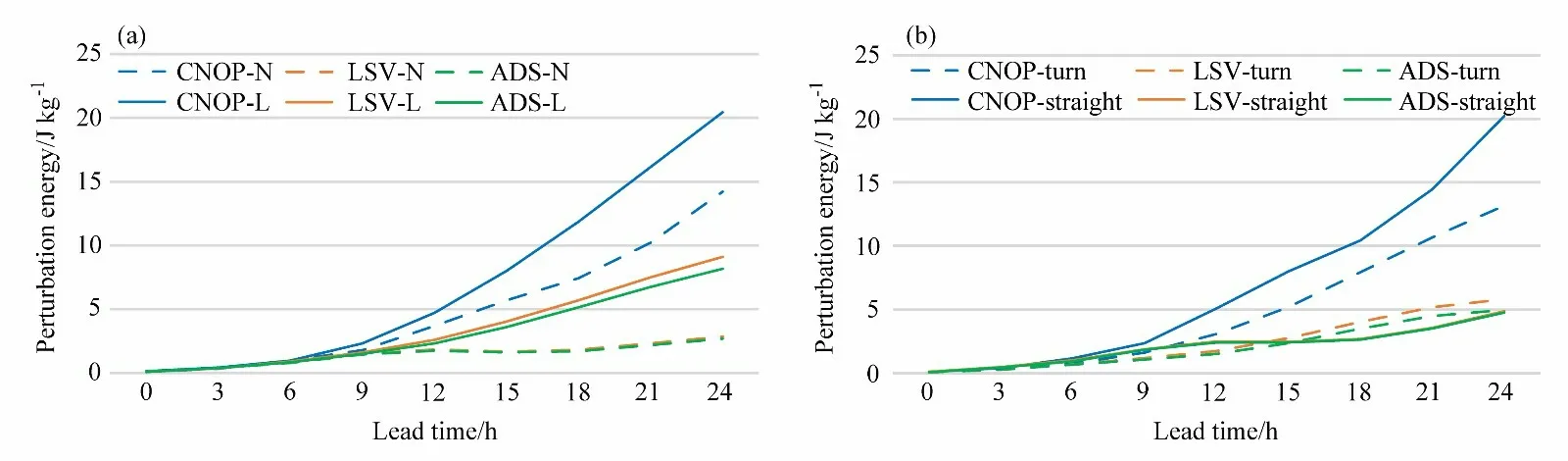
图8 （a）不同非线性程度下CNOP、LSV、ADS 方法识别的敏感区内的随机扰动的能量随预报时间的变化，-N 表示非线性较强的台风，-L 表示非线性较弱的台风；（b）转向型与直线型台风中CNOP、LSV、ADS 方法识别的敏感区内随机扰动能量的平均发展情况，-turn 表示转向型，-straight 表示直线型Fig. 8 (a) The average energy development of the random perturbations respectively added in CNOP-, LSV-, and ADS-identified sensitive areas with lead time for strong nonlinear typhoons (-N) and weak nonlinear typhoons (-L). (b) The average energy development of the random initial perturbations respectively added in CNOP-, LSV-, and ADS-identified sensitive areas for straight typhoons (-straight) and recurved typhoons (-turn)

5 总结与讨论

本文深入分析了伴随敏感性（ADS）方法、第一奇异向量（LSV）方法、以及条件非线性最优扰动（CNOP）方法在目标观测敏感区识别方面的原理，在此基础上，提出了非线性程度的概念和计算方法，并以转向型和直线型台风为例，考察了不同类型台风的非线性程度，分析了上述三种方法在不同非线性程度下识别的敏感区的异同，同时对比了转向型和直线型台风的敏感区的差异，并通过敏感性试验探讨了在不同非线性程度下以及在转向型与直线型台风中，预报对敏感区内初值的敏感性程度，进而探讨台风目标观测在不同情况下的有效性。结果表明，对于非线性较弱的台风，三种方法识别的敏感区较为相似，在敏感区内添加随机扰动对台风预报效果的影响差别也较小，在这种情况下，由于ADS 方法在计算过程中不需要迭代求解，具有较高的计算效率，因此可以采用ADS 方法识别敏感区。而对于非线性较强的台风，ADS 方法和LSV 方法识别的敏感区依然较为一致，然而它们和CNOP 方法识别的敏感区有较大区别，由敏感性试验显示，CNOP 敏感区内随机扰动增长最大，对预报有更大的影响，说明对于非线性较强的台风，LSV 敏感区和ADS 敏感区不如CNOP 敏感区有效，此时推荐用CNOP 方法去识别敏感区。此外，研究发现，转向型台风的非线性程度差别比较大，或者特别强，或者特别弱；而直线型台风非线性程度居中，不同台风个例之间的非线性程度差别较小。对于转向型台风，敏感区主要位于行进路径的右前方，而对于直线型台风，敏感区主要位于初始台风位置的后方。上述结果表明对于转向型台风，其行进前方会出现重要的阻拦或干预，而对于直线型台风其前行路上受到的影响较小。最后研究还发现，不论非线性强还是非线性弱，转向还是直行，CNOP 敏感区内的随机扰动都是发展最大的，而LSV 敏感区内叠加的随机扰动发展次之，ADS 识别的敏感区内叠加的随机扰动发展最小。对于非线性较弱个例，扰动的发展平均而言要大于非线性较强个例的扰动的发展，这表明，对于非线性较弱个例，预报对初值更为敏感，目标观测效果可能会更为明显。类似地，我们发现对于直线型台风，平均而言CNOP 敏感区内扰动的发展要大于转向型台风扰动的发展，然而由于LSV 敏感区和ADS 敏感区内扰动在直线型和转向型台风中的发展是相当的，因此，预报对初值的敏感性在转向型台风和直线型台风中的差异会因初始扰动所在的区域的不同而不同。当然，上述结论还有待于用更多的个例进行验证。

在本研究过程中，我们发现还有许多问题有待于进一步研究。首先，台风与其敏感区的相对位置是否可以预示出台风前行的方向？再者，由于本文目标函数中选择的度量为干能量，如果选用其他的度量范数，结论是否会有所不同？等等。