诊断重载铁路钢轨波磨WPD-ASSTFT时-频边际谱方法
2022-06-01肖炳环刘金朝解婉茹牛留斌徐晓迪
肖炳环,刘金朝,解婉茹,牛留斌,徐晓迪
(1.中国铁道科学研究院 研究生部, 北京 100081;2.中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081)
波磨是波浪形磨耗的简称,是在钢轨行车面沿着纵向出现的一种类似波浪形状的周期性钢轨不平顺现象[1]。当列车经过波磨区段时会导致轨道-车辆系统振动加剧,产生噪声,对部件产生损坏,加剧工务养护维修难度,产生大量费用。波磨在高速铁路,地铁尤其是重载铁路中经常发生。
关于波磨产生的机理,国内外有多种理论研究。大致可以分为两大类[2]:①动力类成因,由轮轨系统振动的自激、反馈和共振3种振动方式造成;②是钢轨本身材料问题和接触疲劳理论等一些非动力类成因。对于波磨治理,一方面从成因入手,预防波磨产生。另一方面,从检测入手,寻找波磨位置及时打磨,防止波磨恶化,减少维修费用。
于淼等[3]通过分析钢轨波磨区段轮轨间相互作用力以及列车通过波磨区段轨道-车辆系统动态响应发现:当列车通过频率与钢轨Pinned-Pinned频率相近时会引起轮轨系统共振,且轨枕附近整体振动较大,轨枕跨间整体振动较小。刘学毅等[4]建立了轮轨空间耦合振动模型对重载波磨成因分析,提出了轮对粘滑振动-钢轨不均匀磨损的观点。贺佳[5]通过动力学仿真软件SIMPACK建立小半径曲线下列车-轨道耦合模型,发现当列车通过小半径曲线时,轮对的横向自振频率接近或成轨道振动频率的整数倍时,容易产生波磨,且曲线半径对钢轨波磨影响较大。
由于轴箱加速度能直接反应轨道不平顺对轮对的振动特性的影响,Phamov等[6]利用轴箱测量法在不同类型的轨道上进行轴箱加速度测量,将加速度转换为挠度,间接测量钢轨粗糙度。王开云等[7]研究了波磨波长和谷深对轮轨动态性能的影响,发现在钢轨波磨激励下,轮轨间将产生高频动力,相互作用力明显增强,但对构架和车体振动影响不大。刘力[8]运用EMD和小波去噪方法,对轴箱加速度信号进行处理,并利用惯性基准法准确检测出轨道波磨波形。李清勇等[9]通过统计分析钢轨图像中钢轨波磨线和背景线的傅里叶变换系数,发现波磨线的能量集中在频率比较低的区间,而背景线的能量分布比较分散。王林栋[10]多次测量我国高铁钢轨波磨并分析轴箱振动特征,提出基于振动响应的快速检测法,该方法能够快速得到钢轨波磨情况。董伟等[11]提出一种基于小波包能量熵的轨道波磨检测方法,仿真结果显示有波磨区段的小波包能量熵比正常钢轨区段的大。文献[12-13]用连续小波变换分析了钢轨表面凹痕引起的轴箱垂向和纵向加速度的时间-频率响应特性,以查找轨道短波病害,并对病害的严重程度进行划分。在自动识别硌伤时,提出小波变换的边际谱方法度量轮对受到的硌伤冲击[14]。诊断波磨时若只计算时域方向边际谱,无法证明波磨产生的周期性特性。因此在诊断波磨时对边际谱进行拓展,既计算时域方向边际谱同时也计算频域方向边际谱,称为时-频边际谱。
现今利用轴箱加速度信号诊断高铁轨道短波病害已取得很好的效果[15]。本文在诊断重载铁路波磨病害时,借鉴了高铁短波病害的诊断思想并结合时频分析和边际谱方法,提出了WPD-ASSTFT时-频边际谱方法。首先利用WPD-ASSTFT提取重载铁路波磨的周期特性,通过分频带滤波保留不同波长的波磨;然后计算滤波后时频分布的时-频边际谱;最后计算波磨强度因子和能量因子,结合大量分析数据总结出的阈值判断两者是否均超限,若均已超限则判断当前钢轨区段存在波磨病害,并记录波磨波长信息。
1 钢轨波磨时频特性分析方法
重载铁路波磨会造成轴箱垂向加速度信号周期性变化,使用基于小波包分解的自适应同步压缩短时傅里叶变换算法(WPD-ASSTFT)提取波磨区段的周期性特征,其步骤如下:
Step1对轴箱垂向加速度信号x(t)进行三层小波包分解[16],得到8个子信号,记为x1,x2,…,x8。
Step2在不同窗长下对子信号做STFT,并将时频分布最小Renyi熵值对应的窗长作为同步压缩短时傅里叶变换时的最优窗长[17-18]。
Step3对8个子信号分别做同步压缩短时傅里叶变换。
Step4将子信号时频结果相加得到原始信号时频分布。
1.1 小波包分解
对于工程实际中的非平稳信号来说,小波变换的自适应性比传统的时频分析方法效果好。但是小波分解只对低频成分进行分解,高频成分无法被分解[19]。为了改善这一问题,小波包分解应运而生,它能同时分解低频、高频信号。WPD-ASSTFT第一步对轴箱加速度信号x(t)进行三层小波包分解。即
(1)
式中:xi(t)为子信号;t为时间。
轴箱加速度信号经过小波包分解后,波磨对应的周期性成分和其他频率成分会被分解到不同的频带中。
1.2 自适应同步压缩短时傅里叶变换
在不同窗长下对各子信号做STFT,并计算每个时频分布的Renyi熵。并将时频分布的最小Renyi熵对应的窗长参数作为最优窗长。
子信号在对应的最优窗长下做SSTFT[20]:
Step1对于信号x1(t),x2(t),…,x8(t)循环,做STFT。
Step2计算子信号瞬时频率。
Step3在时频平面对信号的瞬时频率进行同步压缩。
Step4提取时频信息平面的脊线,得到每个子信号的时频分布:ASSTFTi(t,f),i=1,2,…,8,f为频率。
Step5将各子信号的时频分布相加,得到原始信号的时频分布为
(2)
2 WPD-ASSTFT时-频边际谱方法
诊断重载铁路波磨WPD-ASSTFT时-频边际谱方法:利用WPD-ASSTFT提取重载铁路波磨区段轴箱垂向加速度的周期性特征,在此基础上借助边际谱,计算能够表征波磨的强度因子,仅依靠信号的强度因子大小不足以判定波磨的存在,因此需要刻画波磨周期性的另一个指标能量因子,将二者与设定阈值对比,判断是否为波磨区段。算法流程见图1。

图1 WPD-ASSTFT时-频边际谱法算法流程
详细计算步骤如下:

Step2由WPD-ASSTFT方法得到各单元轴箱垂向加速度的时频分布为
(3)
式中:ASSTFTji(t,f)为ASSTFT计算得到的子信号时频分布。
Step3将大量重载铁路波磨区段WPD-ASSTFT时频分布与统计获得的重载波磨波长范围结合,确定出轴箱加速度数据时频分布的滤波范围,根据波长分为三个频带:0.04~0.15、0.15~0.30、0.30~1.00 m。
Step4对时频分布进行分频带滤波,得到滤波后的时频分布,以波长0.04~0.15 m为例,其他两种波长类似为

(4)
式中:v为区段平均速度。
Step5计算时-频边际谱
计算移动时域边际谱为
(5)
式中:K为向前加窗的时间窗长;Fs为信号采样频率;r为加窗开始时间,0≤r≤T′,T′为区段最大时间。
计算频域边际谱为
(6)

(7)
Step7计算波磨强度因子CIFj(t)为
(8)
Step8计算能量因子EFj为
(9)
式中:0≤l≤Fs/2,0≤γ≤3。
Step9计算每个单元三种波长范围的强度因子和能量因子,记录最大能量因子及其对应强度因子。
Step10超限判断,提取波磨信息。
3 实例分析
利用WPD-ASSFTT时-频边际谱方法分析重载铁路轴箱垂向加速度信号,诊断钢轨波磨。并验证该方法的有效性和稳定性。实验信号来自国内某重载铁路综合检测车,轴箱加速度传感器采样频率是2 000 Hz。
3.1 重载铁路波磨时频特性
为了验证WPD-ASSTFT能够有效提取出重载铁路波磨区段轴箱加速度的周期特点,现选择检测车通过一段状态良好轨道时产生的轴箱加速度信号作为对比,时频分布见图2。由图2可知,在非波磨区段的时频分布图中无明显局部周期性特征。
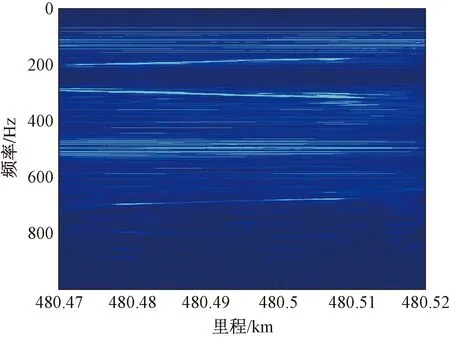
图2 正常轨道时频分布
根据国内某重载铁路现场反馈,上行右轨K273+640—K273+690区段存在钢轨波磨现象,持续约45 m。分析其右侧轴箱垂向加速度,波形见图3。对此段信号做功率谱,结果见图4。由图4可见,71 Hz能量较强,说明轴箱加速度信号中包含波磨造成的周期性成分。
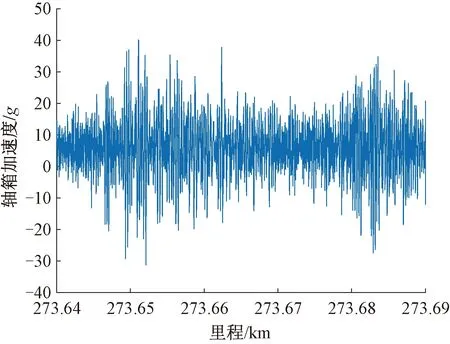
图3 轴箱加速度信号

图4 功率谱
对轴箱加速度(ABA)信号做三层小波包分解,得到8个子信号,结果见图5。各个子信号进行自适应同步压缩短时傅里叶变换,结果见图6。不难发现,经过WPD-ASSTFT分解,轴箱加速度信号中包含的复杂频率成分被分解到不同的子信号中,波磨成分被分解到子信号1中。

图5 子信号
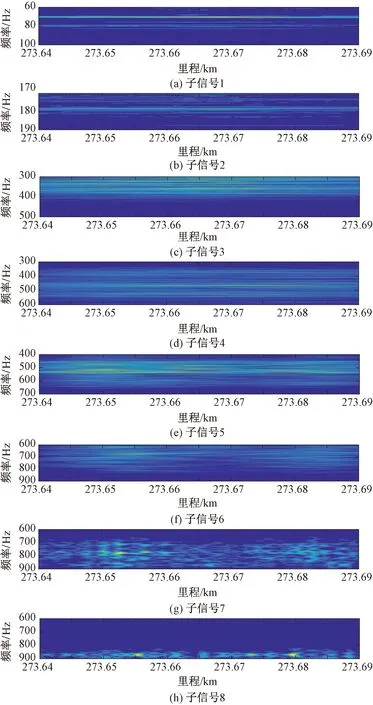
图6 时频分布
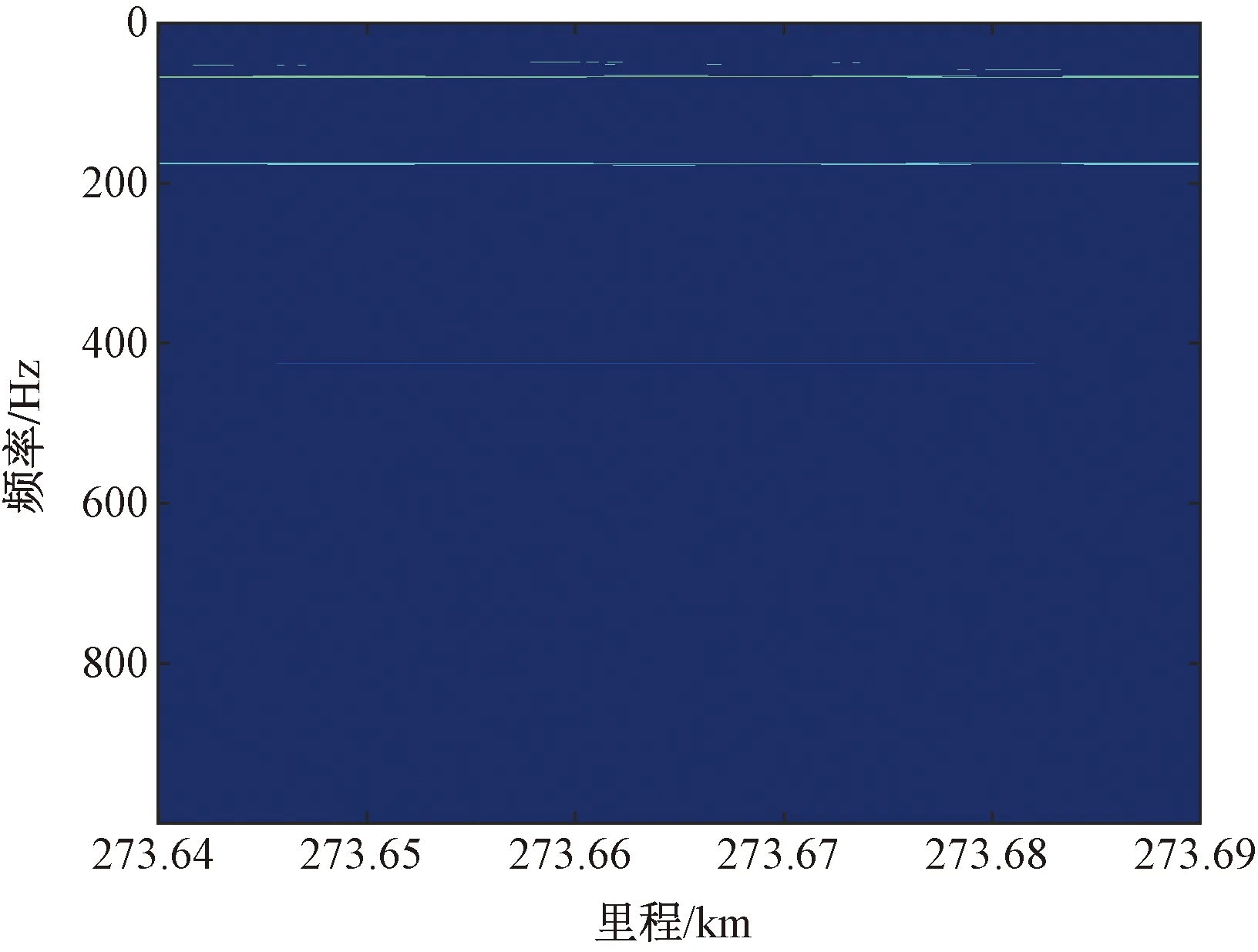
图7 原始信号时频分布
将各个子信号的时频分布相加,得到原始轴箱加速度信号的时频分布,见图7。根据式(4)分频带滤波,并由式(5)、式(6)计算时-频边际谱。然后根据式(8)、式(9)分别计算波磨强度因子和能量因子,结果见表1。能量因子最大时对应滤波范围0.15~0.3 m,主频为71.1 Hz,与功率谱结果对应较好。最大能量因子EF=0.62,对应的波磨强度因子CIF=7.3,0.15~0.3 m滤波后的时频分布见图8(a),频域边际谱见图8(b)。从图8中可观察到71 Hz附近能量最强,且能量因子峰值与时频分布中能量最集中位置一致性很好。

图8 滤波时频分布和频域边际谱

表1 各频带强度因子和能量因子
根据统计的重载铁轴箱加速度各个区段强度因子和能量因子结果,对大量强度因子和能量因子数据做累积分布,并且结合现场复核情况,将阈值设定为达到积分布99%时的值,此时波磨强度因子和能量因子对应的分别为6和0.45,累积分布见图9,因此波磨强度因子的阈值设为6,能量因子的阈值设为0.45。波磨强度因子和能量因子都超过阈值,判定当前区段有波磨现象,与现场情况一致。
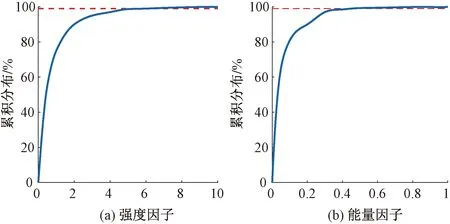
图9 强度因子和能量因子累积分布
3.2 单一病害钢轨波磨分析
利用WPD-ASSTFT时-频边际谱方法诊断重载铁路波磨,对K372+550—K372+600区段左侧轴箱垂向加速度分析。其原始波形见图10。对该区段信号做WPD-ASSTFT得到的时频分布见图11。可以看出信号包含3种周期性成分,其中频率为67 Hz的能量最强。0.15~0.3 m滤波后,64~127 Hz以外的频率成分被滤除,计算频域边际谱,结果见图12。由图12可见,由于滤波带宽设置能量因子仅存在一个峰值。

图10 轴箱加速度信号

图11 时频分布

图12 滤波时频分布和频域边际谱
计算波磨强度因子CIF=7.6,能量因子EF=0.5。波磨强度因子和能量因子都已超过阈值,判定该区段存在波磨。提取最大峰值处的频率为67.4 Hz,根据波长速度和频率的换算公式c=v/f,得到波磨波长为285 mm(该区段平均速度为69 km/h)。
为了验证诊断方法的有效性,进行现场复核。复核时发现该区段钢轨有波磨现象,持续长度约40 m。
复核时使用RMF1100型波磨小车采集K372+550—K372+600区段的静态数据,数据波形和功率谱,见图13。由图13可见,该区段周期性较强,波磨波长289 mm,与WPD-ASSTFT时-频边际谱方法分析的结果吻合,说明波磨特征提取准确,证明了算法的有效性。

图13 静态数据和功率谱
3.3 伴有接头不良的钢轨波磨分析
WPD-ASSTFT时-频边际谱方法除了能有效诊断出重载铁路单一病害钢轨波磨外,还能诊断伴有焊接接头不良的钢轨波磨。
K138+260—K138+310区段钢轨右股除含有波磨外还存在焊接接头不良现象。该区段右侧轴箱加速度波形见图14。由图14可见,K138+295附近是接头不良对轮对造成的高频冲击。
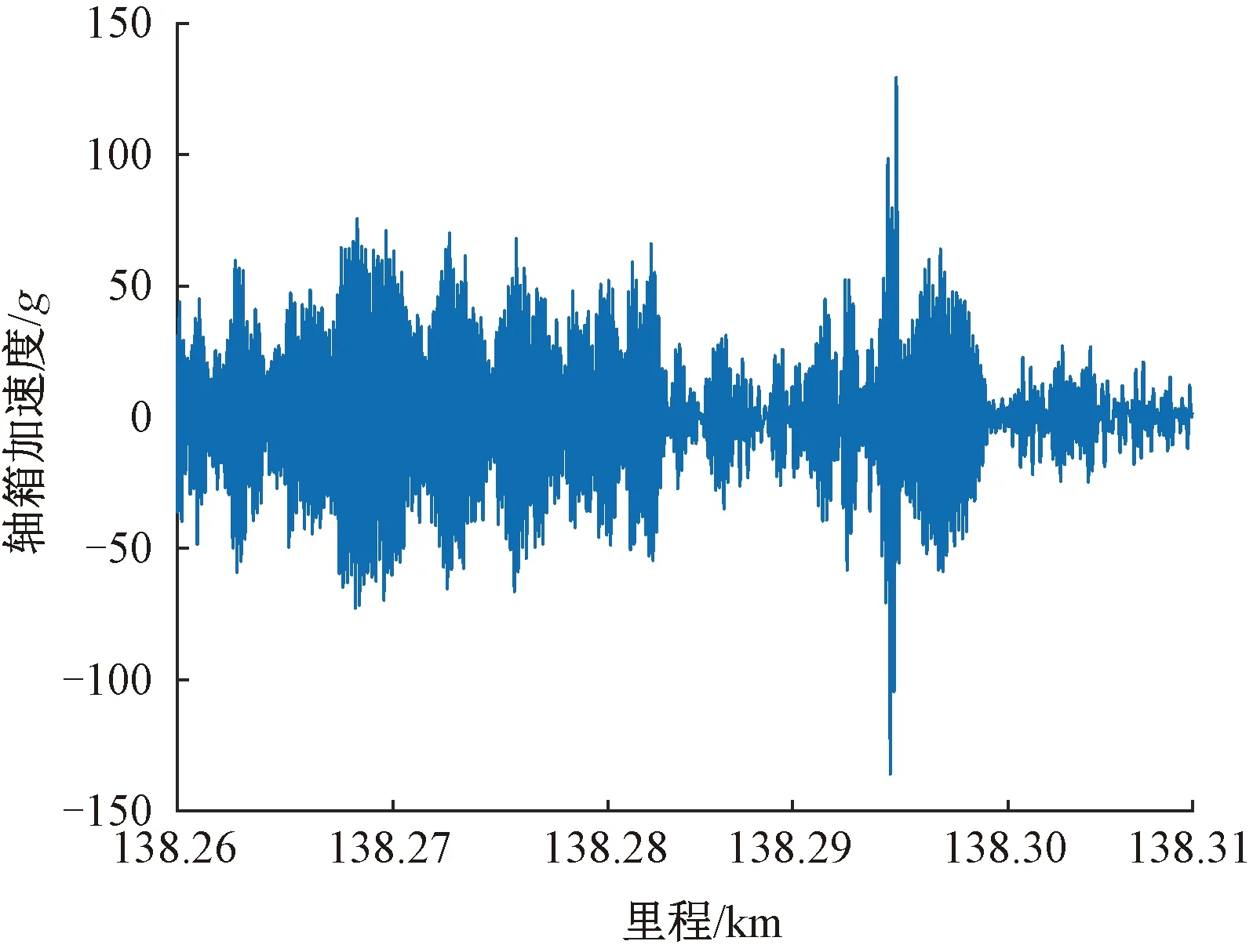
图14 轴箱加速度信号
对该区段做WPD-ASSTFT,结果见图15。由图15可见,除在130 Hz附近存在周期性成分外,K138+295处还有高频冲击成分。该区段信号的时频分布体现了该时频分析算法的优势:信号中同时含有稳态频率和瞬态频率成分时,该方法能够有效识别,并以最佳的分辨率呈现在时频分布中。
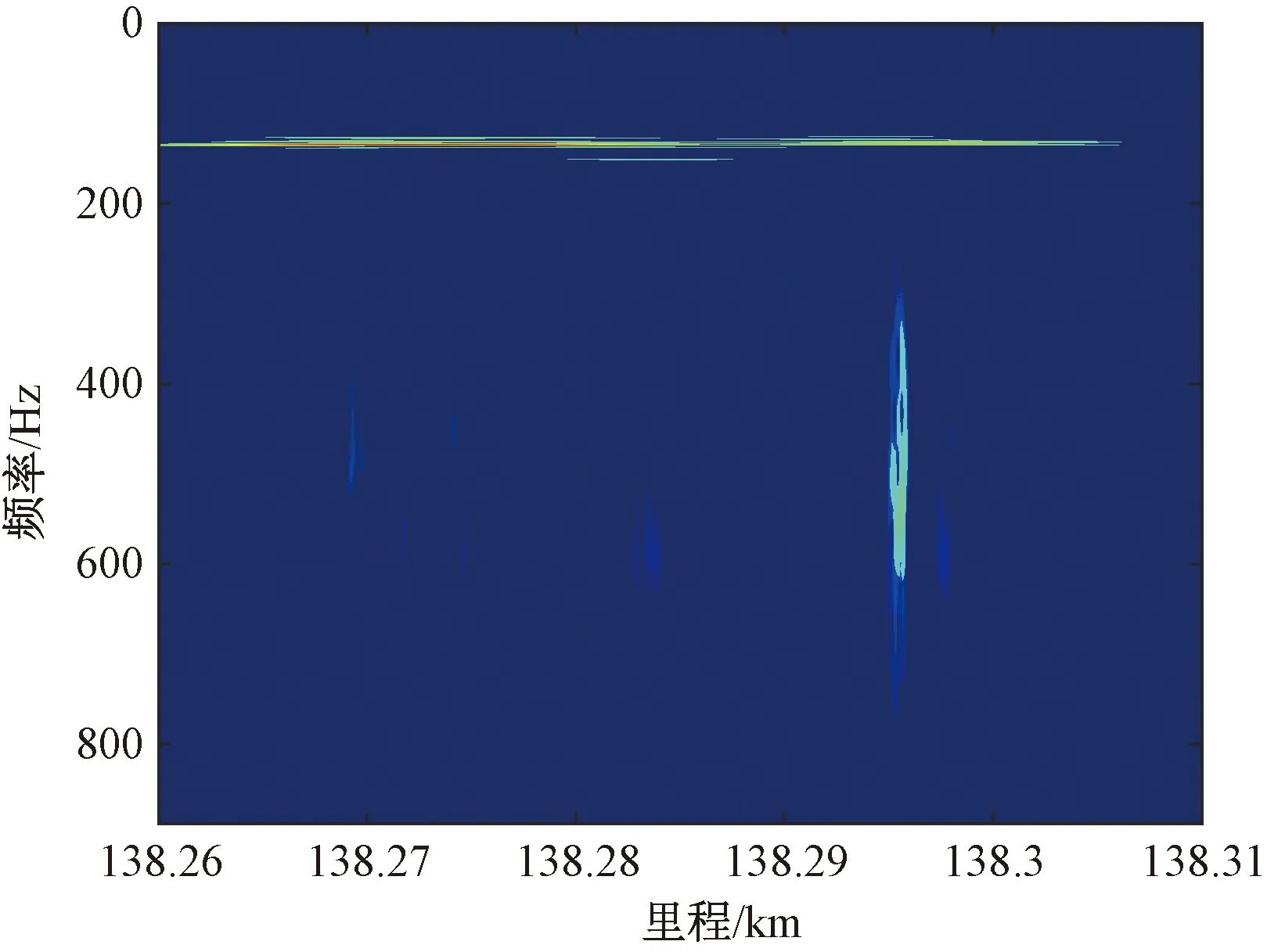
图15 时频分布
高频冲击成分的存在必然会影响能量因子和强度因子的计算,发生波磨漏识、误识。而通过分频带滤波可以完全消除高频冲击成分的影响。滤波后的时频分布见图16(a)。计算波磨强度因子和能量因子,波磨强度因子CIF=8.3,能量因子EF=0.45,频域边际谱见图16(b)。

图16 滤波时频分布和频域边际谱
波磨强度因子和能量因子都超过阈值,判定该区段存在钢轨波磨。且能量因子峰值位置对应频率为131 Hz,计算得到波磨波长128 mm。
通过复核,现场存在波磨现象,且波磨区段还存在焊接接头不良。使用电子平直尺测量接头不良处1 m范围内的轨面平直度并做功率谱,结果见图17。该区段波磨波长129 mm,与分析结果高度一致。WPD-ASSTFT时-频边际谱方法不但能有效诊断单一病害波磨而且还能诊断伴有焊接接头不良的波磨。
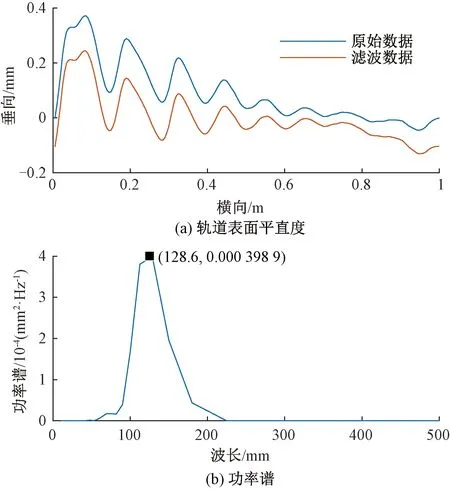
图17 K138+295附近1 m静态数据和功率谱
3.4 算法稳定性分析
为了验证WPD-ASSTFT时-频边际谱方法的稳定性,对同区段不同月份的轴箱垂向加速度进行分析。检测车第二次经过K372+550—K372+600的波形见图18。WPD-ASSTFT分析结果见图19。
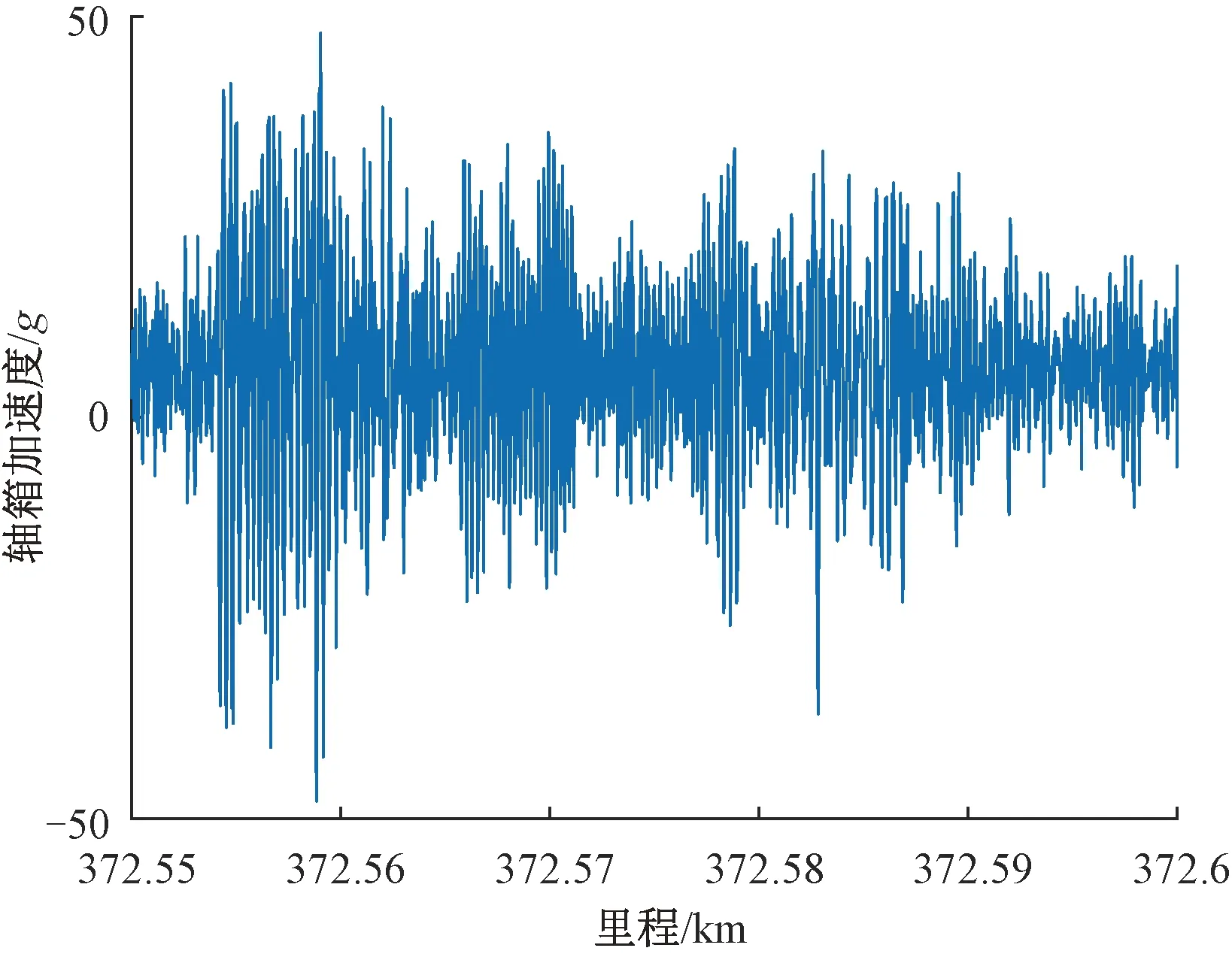
图18 轴箱加速度信号

图19 时频分布
根据WPD-ASSTFT时-频边际谱方法分析结果:0.15~0.3 m波长内的能量因子峰值位置对应频率为67.4 Hz,波磨强度因子CIF=7.5,能量因子EF=0.48。
对比第一、第二次的频域边际谱,结果见图20。由图20可见,峰值位置均与时频分布能量最大位置对应,且两次结果重合度极高。综上分析可得该算法有良好的稳定性。
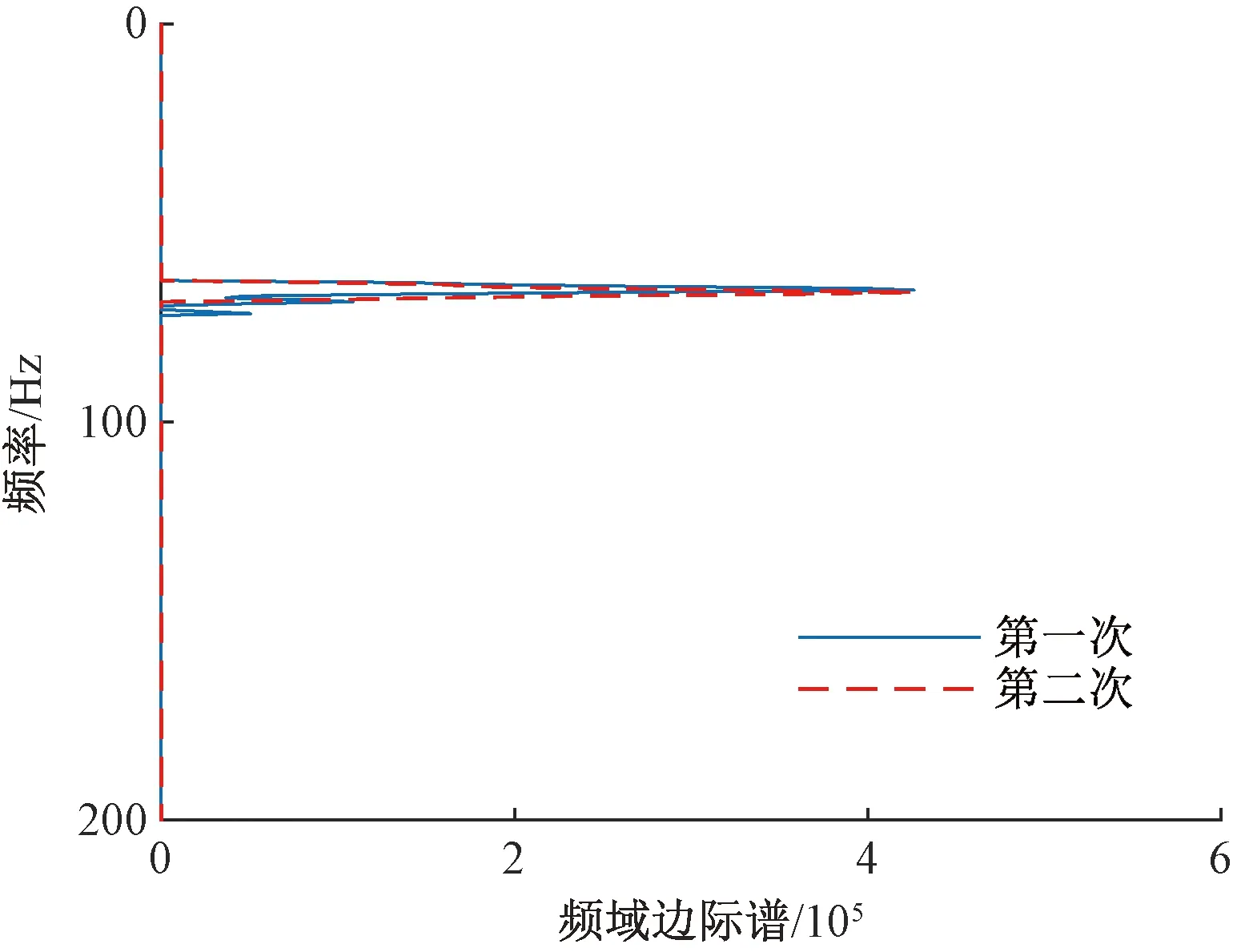
图20 频域边际谱对比
利用WPD-ASSTFT时-频边际谱方法诊断重载铁路波磨,8、9、10月份的检测数据得到的波磨位置见图21(取前500 km,黄色圆圈代表诊断出有波磨的位置)。经统计,波磨位置重合度较高,经过现场复核统计,诊断准确率达88%。

图21 检测结果
本节利用利用WPD-ASSTFT时-频边际谱方法诊断重载铁路波磨,根据诊断结果和复核情况证明了算法的有效性。通过对比同区段两次不同轴箱垂向加速度的时-频边际谱证明了算法的稳定性。并且在应用过程中体现了WPD-ASSTFT在时频分布分辨率方面的优势。并且诊断准确率较高。
4 结论
提出了一种诊断重载铁路波磨的WPD-ASSTFT时-频边际谱方法,该方法通过时频分布提取出波磨区段的特征信息,结合大量数据的时频分析结果对时频分布分频带滤波。计算得到波磨强度因子和能量因子并与所设阈值比对判断是否存在波磨,提取波磨区段波长。通过现场复核和对比两次同区段数据证明了该算法的有效性和稳定性。经实践检验,该方法能够很好地指导重载线路养护和维修钢轨波磨,满足工程在线应用的需求。
