WRF/CALMET/BP预报系统对内陆山区风电场的一次滚动预报检验
2022-06-01刘伟李艳杜钦
刘伟 李艳 杜钦
(1 南京信息工程大学 大气科学学院 南京 210044;2 呼伦贝尔市气象台,内蒙古 呼伦贝尔 021000;3 重庆市气象科学研究所,重庆 401147)
引 言
能源是世界发展和经济增长的源动力,是人类文明生存的基础,但随着石油、煤炭等传统能源的迅速开发和利用,其产生的污染物以及CO2等温室气体对环境的危害也日益突显。风能作为一种无污染的可再生能源具有巨大的发展潜力,既可以优化能源需求结构,又能有效缓解环境问题。我国风能具有巨大的开发潜力[1-2],但由于风的变化具有波动性和间歇性,风电的不可控性很大,风电场接入电网使电力运行系统不确定性增多,影响供电质量[3]。因此为了增强电网调度的主动性,改善风电场运行管理效能,提高风电发电量比重,准确的风能预报尤为重要。
风能预报的本质是基于风速、湿度等气象要素的预报结果,借助数值天气预报技术,使不稳定的风电可预知,从而有效减轻风电对电网冲击的影响,提高风能资源的利用效率和风电场的运行效益。目前,风能预报的主要方法有统计预报、动力预报以及动力—统计相结合的方法等[4]。统计预报通过建立风电场大气资料和风电量输出资料之间的经验关系以及合理的经验系数,进行外推直接得到风电量预报值,该方法更多地考虑风场的统计规律,具有计算简单、运行速度快的特征,常用的方法有持续法、时间序列法(ARMA)、人工神经网络法、卡尔曼滤波法等。但统计预报方法过分依赖观测资料且预报时效短[5]。动力预报是基于大气质量、动量、能量守恒以及大气状态方程等基本物理原理模拟大气运动的计算流体动力学模式(Computational Fluid Dynamics, CFD),也称为物理大气模式[6]。动力预报可延长风电预测的有效时间,目前动力预报在72 h内的预测水平达到了80%以上,是风电功率短期预报的有效方法之一,相对于统计预报,更适用于复杂地形的风能精细化预报[7]。但大气数值模式是一个离散化的数值模型,在模式模拟过程中描述的大气过程与真实大气过程存在误差,这种误差由于随着积分时间的延长增加而成为制约数值预报准确率的一个重要因素。因此,仅使用统计方法或动力方法进行预报都具有一定的局限性,为了提高风能短期预报的准确性,目前普遍采用动力和统计相结合的预报方法,该方法适用于电网调度和电力市场管理,时效通常为0~48 h[8]。
国外基于动力统计相结合的风能预报开展地较早,1990s中期,美国的True Wind公司就已经将其研发的Ewind风能预报系统投入使用,该模型通过自适应统计方法来消除物理模型的系统误差[5-9]。为提高预报精度,由7个国家的23个机构共同参与研发的ANEMOS项目使用多个物理模型与统计模型相结合对海洋和陆地的风电场短期风速及风功率进行预报,且预报误差仅有10%左右[10],我国风电场风能预报工作虽然开展较晚,但发展较快。江滢等[11]利用多种统计方法对甘肃两个风电场风速进行订正,误差率减少了19.6%~10.8%;王彬滨等[12]利用BP神经网络对MM5模式的预报结果进行修正,取得了较好的预报效果;程兴宏等[13]利用中尺度WRF模式和自适应偏最小二乘回归法相结合,也证实了统计订正方法可以有效提高风电功率短期预报的准确率。许杨等[14]利用MM5耦合CALMET模式,对比物理法和动力统计法的预报效果发现,动力统计法更适应复杂山区地形。叶小岭等[15]利用WRF模式和随机森林算法建立集成预报模型,提高了风速预报的精度。
本文以内陆山区重庆市的齐跃山风电场作为研究区域,以中尺度数值模式(Weather Research and Forecasting Model, WRF)与CALMET相结合作为风资源动力预报系统,通过BP神经网络进行统计订正,对2015年11月研究区域内25座测风塔进行高时空分辨率的逐5 min的滚动预报,探讨该动力—统计预报方法对中国典型内陆山区的适用性,检验统计订正方法对动力预报的改善效果,以期提高内陆山区风电场的运行效益,为电网运行的安全性提供有效的保障。
1 资料与方法
1.1 试验区域
重庆市位于我国西南部的长江上游地区,其北部、东部及南部分别有大巴山、巫山、武陵山和大娄山环绕。地势最低处海拔为78.12 m,地势最高处海拔为2 794.72 m。地貌以丘陵和山地为主,坡地面积较大。重庆市西北部和中部主要为丘陵和低山,地势较低,东北部和东南部分别有大巴山与武陵山两座大山脉,地势较高,属于亚热带季风气候。受到地形差异影响,其气候随海拔高度呈现出垂直分异性,这对风能资源的空间分布影响较大,呈现出风速随海拔高度而增大的特点[16]。空间上,风速的区域性差异非常明显,大致的分布特点是东北部东端最大,西部次之,中间地带最小。特殊的地理环境使重庆市的平均风速整体较小,但因为地形的特殊性,像齐跃山等地处山口和河谷的地区风资源仍较为丰富。齐跃山风电场位于重庆市东南部七曜山山脉,隶属石柱县丰都镇。风电场全长约71 km,呈东北—西南向的长条形分布,场内地形复杂。风电场内设置有25座代表测风塔,位于七曜山山峰处,呈西南—东北向排列(图1)。
1.2 数据资料
本文所用到的测风塔资料来自齐跃山25座测风塔2015年11月1—30日不同高度上的风速观测资料以及风机的输出风功率,资料时间间隔为5 min。测风塔观测项目包括风速、风向、气压、温度和湿度等。25座测风塔均为70 m风塔,每座测风塔在10、30、50、60和70 m处分别安装风速计,除70 m高度上安装两套风速计,其余高度上各安装一套风速计,10和70 m分别安装一套风向设备。目前,风机轮毂高度多数在60~70 m,因此70 m风速预报的准确性对风电企业来说至关重要[17]。本文选取了齐跃山风电场70 m高度的风速观测数据以及风机输出功率作为标准样本,用来检验模式预报数据的准确性。此数据基本能够代表齐跃山稳定大气层结状态下的风场分布特征。另外,其时间分辨率是5 min,也能够较好的反映大气层结相对稳定的背景下齐跃山风电场的风场瞬变特征与日变化特点。
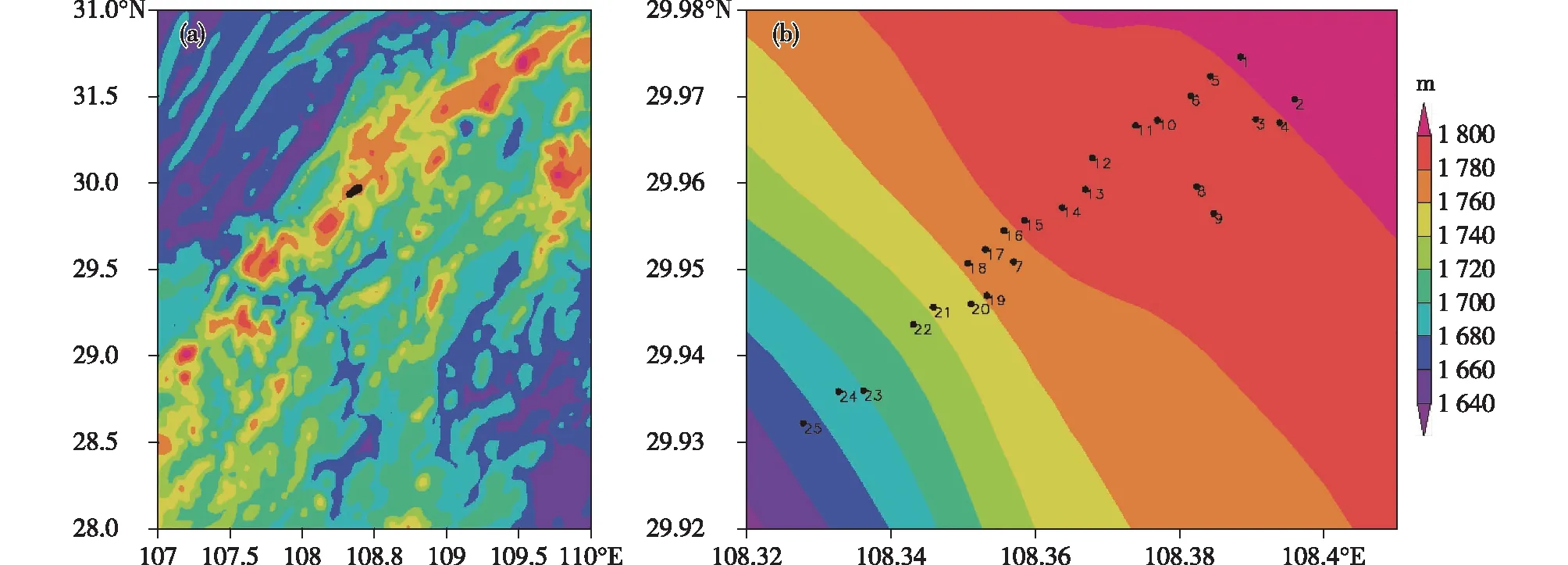
图1 25个风机所处的地理位置及空间分布(阴影代表地形高度,单位:m)Fig.1 Location and spatial distribution of 25 wind turbines (shadow represents topographic height, unit: m)
1.3 WRF/CALMET/BP预报系统
近年来,通过中尺度模式与风场诊断模型CALMET结合来对区域风场进行研究的方法已经被广泛应用[18]。本文以WRF/CALMET为风场动力预报系统,针对2015年11月进行的水平分辨率为3 km,时间分辨率为5 min的24 h风场滚动预报。以WRF的模式输出数据作为驱动CALMET运行的初始场与边界条件,完成风电场的动力预报过程。将动力预报结果与风机观测数据作为BP神经网络的训练集与检验集,对该地区风能资源进行统计订正预报,最终给出风电场每台风机的每5 min的24 h滚动预报。
1.3.1 WRF/CALMET模式
WRF模式是由美国国家大气研究中心(NCAR)、国家环境预报中心(NCEP)及其他部门联合开发的新一代高分辨率中尺度天气预报数值模式[19]。WRF采用三重双向嵌套网格,水平方向分辨率为27、9和3 km,最外层网格覆盖了中国大部、南海及部分太平洋地区,最内层网格覆盖了整个研究地区。垂直方向上设置51层,模式顶设在50 hPa。模式的微物理过程参数化方案包括:WSM3简单冰方案、RRTM长波辐射方案、Dudhia短波辐射方案YSU边界层参数化方案、Kain-Frisch积云参数化方案以及Noah陆面参数化方案。模式的初始场与边界条件均采用FNL (Final Operational Global Analysis) 全球再分析资料,该资料具有空间分辨率高、资料长度长且连续,并且融合了大量的卫星反演资料及站点观测资料的优点,近些年来被广泛应用于气候的诊断、天气预报及数值模式的研究中[20]。
CALMET模式是非稳态拉格朗日烟团模型CALPUFF中的网格化风场模块,其核心为诊断风场模块与微气象模块,结合地形数据模拟输出逐时风场、三维温度场和混合层高度等气象要素,其生成的风场垂直方向最多可达25层,适用于模拟从几十米到几十千米的中小尺度范围。中尺度数值模式由于受模式设计和计算条件限制,不能提供更高水平分辨率的输出产品,因此利用CALMET风场诊断模型进行降尺度处理,对中尺度数值模式模拟风场进行地形动力学、坡面流、地形阻塞效应调整,产生第一步风场。导入观测数据后,通过插值、平滑处理、垂直速度计算、辐散最小化等产生最终风场。微气象模块根据参数化方法,利用地表热通量、边界层高度、摩擦速度、对流速度、莫宁—奥布霍夫长度等参数描述边界层结构。本文中CALMET所选区域中心为(30.0°N,107.8°E),格点数为500×500,水平分辨率为1 km。
1.3.2 BP神经网络法
风电场风速预报是一个复杂的非线性过程,人工神经网络通过模拟人脑的信息处理机制,在很大程度上简化了建模工作,使预报的结果更为精准[21]。本文选用的BP模型是目前应用最为广泛和成熟的方法之一,该模型学习算法的基本原理是梯度下降法,通过调整权值使期望值与网络的实际输出值的误差最小。BP神经网络包括输入层、隐层和输出层,其中隐层可以有一层或多层,同层节点中没有任何连接。本文选用三层BP神经网络对齐跃山25座测风塔的数值预报风速产品进行模式的解释应用,其结构如图2,图中输入层设有n个输入节点x1,x2,……,xn,输出层设有m个输出节点y1,y2,……,yn,隐含层有θj个神经元;ωij是输入层与中间层的连接权值,ωjk是中间层与输出层的连接权值。在实际应用中,由于神经网络输出层的激活函数是有限的,因此需要将网络训练的目标数据映射到激活函数的值域。例如本文的输出层采用的S形激活函数,它的值域限制在[0,1]之间,因此必须对输入风速数据进行归一化处理。文中采用了两种归一化函数,其一为premnmx函数,主要用于归一化训练集数据;其二为tramnmx函数,主要用于归一化预测集数据。经过归一化的输出风速数据范围限制在[0,1]之间,要得到实际的风速值,则需再一步反归一化,文中所用的反归一化函数为postmnmx,主要用于输出的风速数据。
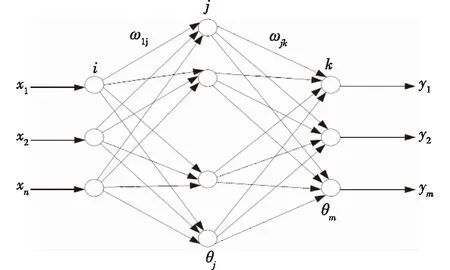
图2 BP神经网络模型结构[22]Fig.2 Model structure of BP neural network[22]
1.3.3 模型建立
本文针对研究区域内测风塔2015年的11月的风场单独建模,建模时,将风速序列分为训练集及预测集,训练集选取样本的前1/3,预测集选择样本的后2/3。为缩短仿真时间,考虑到风向等信息对风速影响较小,仅以风速作为网络单一输入。在本次试验设置中,训练集中的训练向量为2015年11—10日25座测风塔的风速观测数据和WRF/CALMET风速模拟值,时间间隔为5 min,共5 760个数据。将这些数据输入BP神经网络,从而预报11月11日24 h每5 min的70 m风塔风速值,根据70 m风塔的风速与该风机输出风功率的拟合关系预报当日24 h每5 min的风机输出功率。根据上述流程,采用预报间隔为24 h的循环预报方法,预报2015年11月11—30日的每5 min的70 m测风塔的风速和风机输出功率。
2 齐跃山11月风能资源特征
2.1 空间分布
齐跃山风电场的70 m风速和风机输出风功率的区域平均值分别为6.15 m·s-1、554.34 kW·min-1(图3),整体呈现西北高、东南低的特征,最大值分别为7.34 m·s-1、779.75 kW·min-1,最小值分别为4.38 m·s-1、252.7 kW·min-1。对比2015年《中国风能太阳能资源年景公报》的统计结果,全国各省陆面70 m高度平均风速在3.8~6.5 m·s-1之间,齐跃山风电场11月70 m可利用风能资源较为丰富。
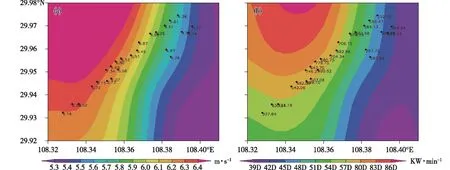
图3 2015年11月25个风机70 m高度风速(a, 单位: m·s-1)和风机输出功率(b, 单位: kW·min-1)的月平均值Fig.3 Monthly average of wind speed(a,unit: m·s-1) and wind power(b,unit: kW·min-1) at 70 m height of 25 wind turbines in November 2015
2.2 日变化及频率分布
重庆地区风的日变化受小气候影响明显,齐跃山风电场风速变化整体呈现傍晚增大,夜间减小的变化趋势,其中最小值出现在16时(北京时,下同),平均最小风速为5.08 m·s-1,最大值出现在23时,平均最大风速为6.88 m·s-1,06—08时风速出现短暂增大过程。日风机输出功率也呈现先减小后增大的趋势,最小值出现时间为14时,最大值出现时间为23时,范围为473.86~922.94 kW·min-1(图4a)。
风电场风机实际发电过程中,在3~25 m·s-1风速段内,风机能够正常工作,图4b为11月风速与风能频率的直方分布,可知,2015年11月70 m风速最大值为19 m·s-1。小于3 m·s-1的样本占总样本数的21.73%,3~8 m·s-1风速段样本占样本总量的51.31%,8 m·s-1以上风速出现的频率为26.96%。该地区主要风速段为3~8 m·s-1,风速可利用率达到78.27%。

图4 25个风机平均风速(单位:m·s-1)和风功率(单位:kW·min-1)的日变化(a)以及累计频率分布(b)Fig.4 Daily variation of (a) average wind speed (unit: m·s-1) and wind power (unit: kW·min-1) and (b) cumulative frequency distribution of 25 wind turbines
3 WRF/CALMET/BP预报风能检验
风能预报误差的检验分为绝对检验和相对检验。绝对检验提供的是独立于其他方法的预报系统的估量,如均方根误差(Root Mean Square Error, RMSE)、平均绝对值误差(Mean Absolute Error, MAE)、相关系数(Correlation Coefficient, CC)和标准差比率(Standard Deviation Ratio, SDR)等,相对检验是一个预报方法对于其他方法性能的评估,最常用的相对检验方法是对持续性预报方法的技巧评分。本文使用泰勒图通过均方根误差、相关系数和标准差比率等统计量,对统计订正前后的预报结果进行了总体效果检验、日变化效果检验和不同风速等级的误差检验,从不同角度检验该模式的预报精度。
泰勒图常用于评价模式的精度[23],它能够将三维评价指标的相关信息在二维平面图中表示出来,可以全面清晰反映多模式或同模式多站点的模拟能力,泰勒图上的每个点代表不同站点预报的结果,该点到坐标原点的距离表示模拟结果与实测风速的标准差比率,表示模式对中心振幅的模拟能力,标准差比率越接近1.0表示模拟能力越好,其所在半径与水平方向夹角的余弦值代表预报与观测的相关系数,该点到REF(表示观测参考点)的距离代表预报与观测的中心化均方根误差。因此,泰勒图不仅可以比较全面的反应预报与观测时间序列的变化趋势、振幅及误差程度,而且可以反映出位相误差和振幅误差对于均方根误差的贡献。
3.1 总体效果检验
风机输出功率的预测结果主要取决于风速预报的准确性,故本文仅对风速预报结果进行检验。由图5可知,WRF-CALMET模式对于风速的模拟效果不稳定,经过BP订正后,预报风速更贴近实况风俗,整体风速误差值减小。

图5 实况风速与订正前后风速对比(a,单位:m·s-1),以及订正前后风速误差值(b,单位:m·s-1)Fig.5 The comparison between the observed wind speed and the wind speed before and after the revision (a, unit: m·s-1), and the error value of the wind speed before and after the rivison (b, unit: m·s-1)
为了定量比较模式预报能力的整体情况,分别计算了25个风机的误差统计量,并将其表示在泰勒图上,图6显示了25个风机在WRF-CALMET模式(红色)下的预报结果,以及经过BP神经网络订正后(蓝色)的预报结果,可以看出,WRF-CALMET模式模拟结果与实测风速的标准差比率主要集中在0.9~1.1范围内,说明动力模式对中心振幅的模拟能力较好,经过BP神经网络订正后,标准差比率分散在0.25~1.25范围内,说明统计订正后,预报结果的振幅变小,标准差比率相对于1.0更加离散,预报结果趋于均值。从相关系数角度来看,模式预报和订正结果的相关系数均小于0.3,预报结果与观测值的相关性较弱,模式对于风速变化趋势的模拟能力有待提高。从中心化均方根误差角度来看,统计订正后,半数风机的预报结果到参考点(REF)的距离更近,中心化均方根误差更小,预报结果更贴近实况风速。总体来看,WRF-CALMET模式对于中心振幅的模拟能力较好,而经过BP神经网络订正后,预报结果趋于均值,但超过半数风机的中心化均方根误差降低,预报结果更贴近实况风速,但是,由于模式训练数据集较少,故预报结果与实况风速相关性较低,对于风速变化趋势的预报能力有待提高。
3.2 日变化检验
风速的日变化直接影响风电功率的输出,造成对电网的冲击,所以我们需要讨论风速预报的日变化效果,以期减缓这种影响,更好地服务于风电企业。从25个风机风速日变化与模拟预报风速日变化的对比(图7)来看,模式对于25个风机风速预报适应性各不相同,订正前后预报风速与实况风速的误差值各有不同,其中1、7、8、9和16号风机的预报误差较大。
为了定量说明全天各时次模式预报能力的情况,采用与图6相同的计算方法分别将全天各时次的25个风机误差统计量表示在泰勒图上(图8)。从相关系数角度来看,WRF-CALMET模式模拟结果与实况风速的相关系数在0~0.5范围内波动,其中12—19时模拟结果相关系数最大值达到0.4~0.5,为全天峰值阶段,说明动力模式在午后至傍晚时段对于风速变化趋势的模拟效果有所改善。而BP订正后的模拟风速与观测值的相关系数主要集中在0~0.25区间内,个别风机在午夜至凌晨时段相关系数增大到0.4左右,说明经过BP神经网络对于风速值的订正,动力系统对于风速变化趋势的模拟效果减弱。从标准差比率的角度来看,除去18—22时,风机预报效果偏离参考点,其余时段动力模式的标准差比率均集中在1.0附近,统计订正后,在12—17时,标准差比率集中在1.0附近,全天中该时段中心振幅误差较小。从标准化均方根误差的角度来看,在12—16时,无论是WRF/CALMET模式模拟的风速还是经过BP神经网络订正后的模拟风速结果均有所改善,泰勒图中风机位置距离参考点(REF)的距离减小。综上,该模式对于正午至傍晚时段的风速模拟效果较好。
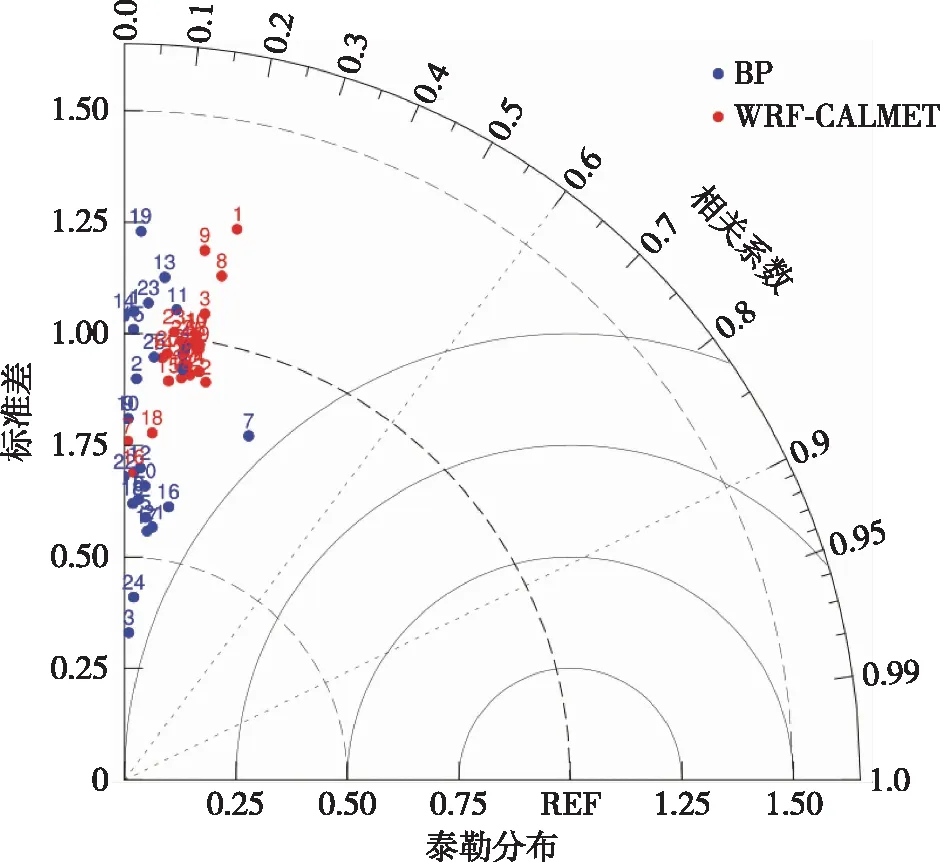
图6 模式模拟订正前后25个风机泰勒分布Fig.6 Taylor diagram of 25 wind turbines before and after revision
3.3 不同等级风速预报检验
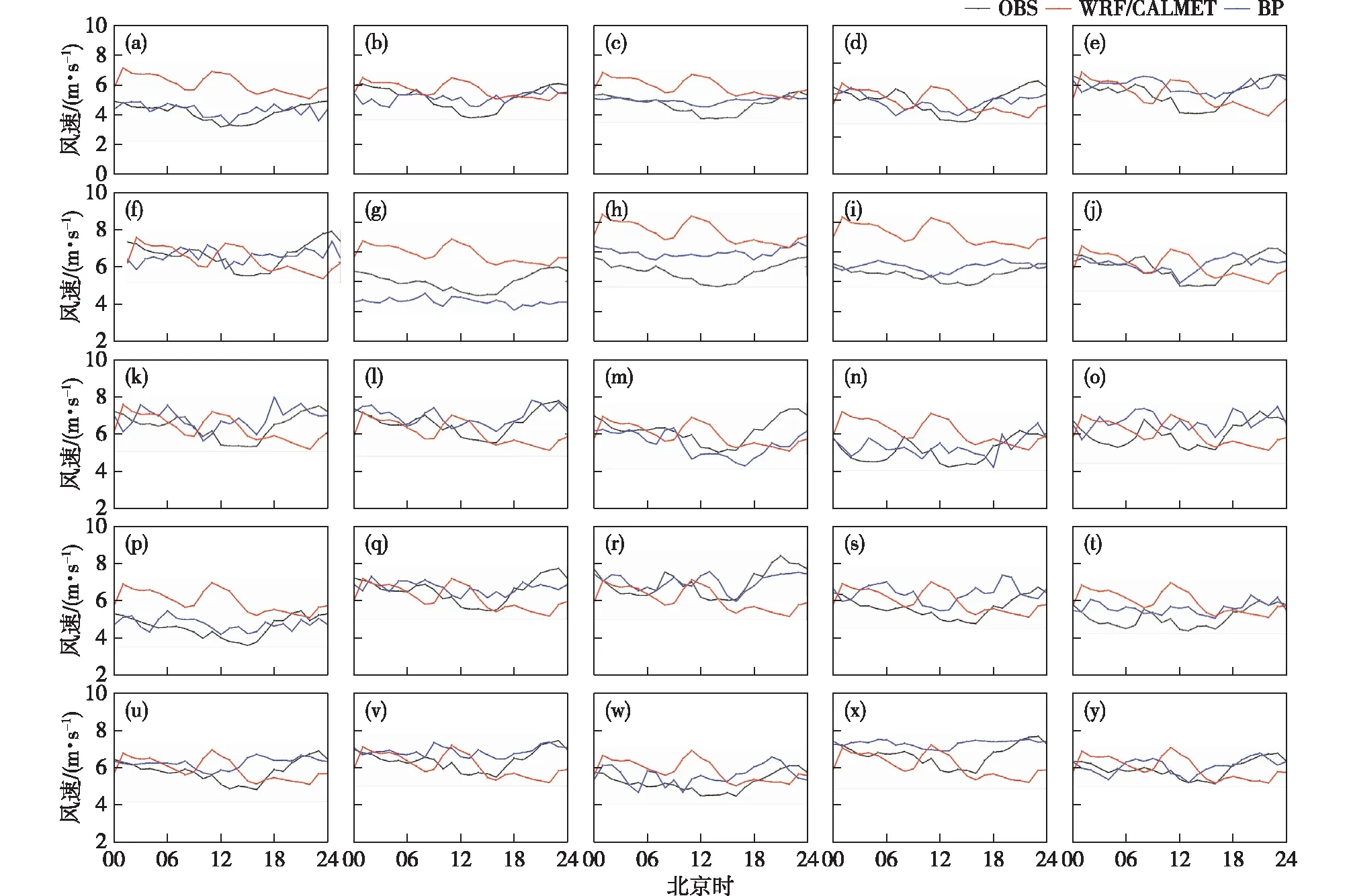
图7 25个风机的观测风速(OBS)、CALMET模拟值和BP订正值的日变化(a—y分别为1~25号风机,单位:m·s-1)Fig.7 Diurnal variation of observed wind speed and the wind speed before and after the revision of 25 wind turbines(a-y stand for 1-25 turbine,unit:m·s-1)
在风电场风机实际发电过程中,风速达到3 m·s-1左右,风机开始启动;3~8 m·s-1时,风机逐渐运转,产生功率缓慢上升;当达到8~14 m·s-1时,风机产生功率快速增长;在14 m·s-1时,达到额定风速,25 m·s-1时达到切出风速,风力机停止运转,因此14~25 m·s-1时,风力机稳定工作,发电功率平稳[21]。所以针对风机实际运行情况,将风速大小分为3个阶段进行检验分析,分别为3~8、8~14和14~25 m·s-1。由于齐跃山风电场风速分布主要集中在3~8和8~14 m·s-1风速段,部分风机并未观测到大于14 m·s-1的风速数据,故图9c中14~25 m·s-1风速段存在缺测值,部分风机未在图中显示。从标准差比率角度来看,动力模式对于低风速段(3~8 m·s-1)风速段的模拟效果最好,随着风速增大,标准差比率更加偏离1.0,对于中心振幅模拟的准确率降低,且结合表1可以看出,统计订正前后的风速模拟结果均存在随着风速增大,均方根误差和标准差比率增大,模拟结果准确率降低的情况。
经过统计订正后,中风速段(8~14 m·s-1)的标准差比率明显减小,更加靠近1.0。结合表1分析,在风速的3个阶段中,经过统计订正后,预报值的均方根误差均减小,修正效果显著。各站点由低风速阶段到高风速阶段预报准确率分别提高了11.5%、14.6%、11.2%,显示该订正方法对8~14 m·s-1风速段的订正效果最为显著,其他两个风速段的订正效果稍差。
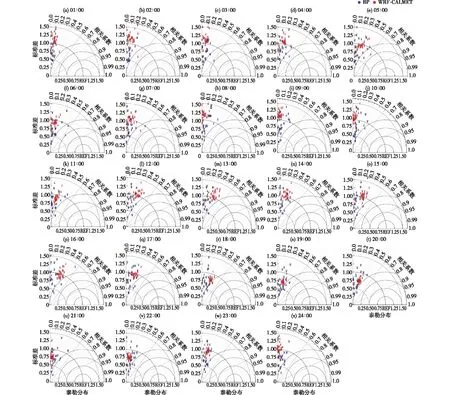
图8 同图6,但为全天各时次Fig.8 The same pictures for each hour per day as fig.6
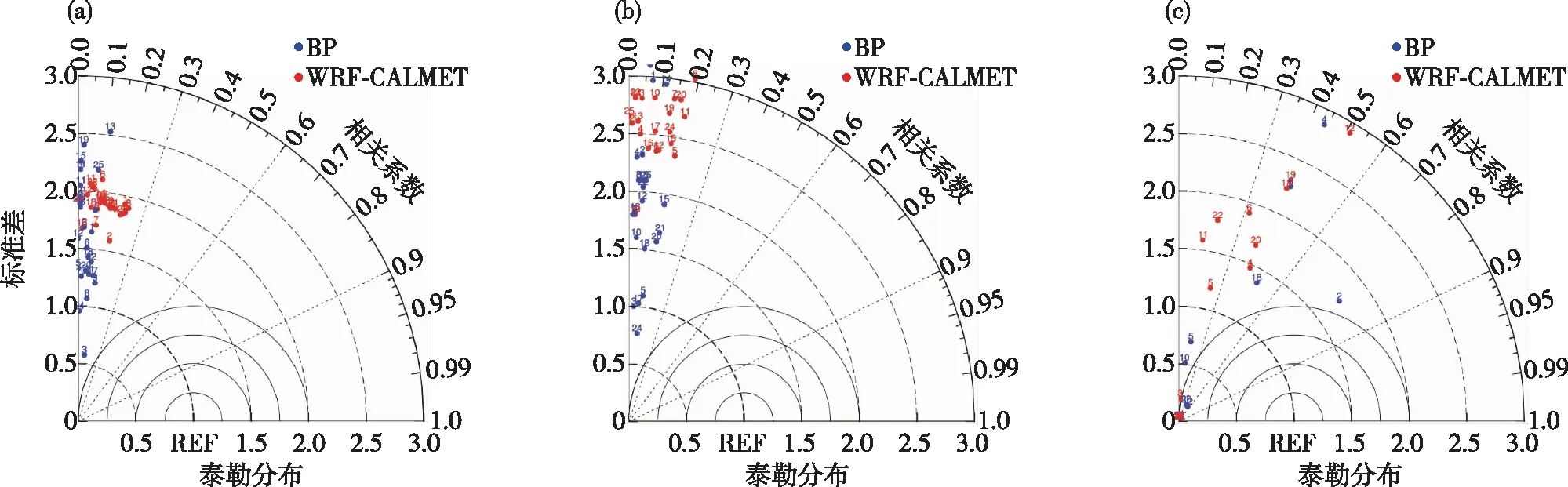
图9 不同风速等级订正前后泰勒分布: (a)3~8 m·s-1; (b)8~14 m·s-1; (c)≥14 m·s-1Fig.9 Taylor diagrams of different wind speed classes before and after statistical revision: (a)3~8 m·s-1; (b)8~14 m·s-1; (c)≥14 m·s-1

表1 统计订正前后不同风速等级均方根误差平均值对比Table 1 Comparison of average RMSE of different wind speed classesbefore and after statistical revision
4 结论
准确的风能预报可以提高风能的利用率,促进风电产业的发展。本文以重庆市齐跃山风电场25台风机为例,利用2015年11月逐5 min的风能观测数据,以中尺度数值模式WRF/CALMET作为风电场动力预报系统,以BP神经网络法(BP-ANN)作为风电场的统计订正预报系统,对齐跃山风电场进行了时间分辨率为5 min的24 h风速、风功率的滚动预报试验。主要结论如下:
(1)使用泰勒图将模拟结果与实测风速的标准差比率、相关系数和中心化均方根误差3个评价指标在二维平面图形中表示出来,从而评估模式模拟效果的优劣。对比分析发现,WRF/CALMET模式对于风速中心振幅的模拟能力较好,但是经过BP神经网络订正后,模拟结果会出现趋于均值的现象,整体风速波动减弱。由于训练集数据较少,故统计订正前后,风速模拟值与观测值的相关系数均较小,说明WRF/CALMET/BP模式对于风速变化趋势的模拟效果不理想,模拟值相位误差较大。WRF/CALMET/BP预报系统的风速预报误差随着风速的增大而增大,对3~8 m·s-1风速段的预报效果最好,其中,BP神经网络对中风速段(8~14 m·s-1)预报结果的订正效果最明显。
(2)在山区,各测风塔所处的下垫面情况复杂多变,由于局地环流的影响使得流经山区的气流改变方向,所以在山区即使是相邻的两地,风速、风向以及风压也往往会有很大的差别。而数值模式由于模式本身的分辨率,下垫面数据及陆面过程和网格的局限性,很难准确捕捉测风塔所处下垫面的真实地形、地貌条件。因此,相对于平原地区,模式不能很好地模拟复杂山区的局地小尺度系统,造成系统预报误差较大。并且,当大气层结比较稳定时,风速往往较低且稳定少变,数值模拟的风场预报误差较小。但是当大气出现层结不稳定,或是出现天气现象变化时,小尺度天气系统的差异以及湍流等现象本身的复杂性等,使预报精度受到了影响。
(3)值得注意地是,BP神经网络订正会削弱WRF-CALMET系统对于风速变化趋势的模拟效果,推测可能原因为,BP神经网络的特点是信号的向前计算与误差的反向传播,整个网络在训练过程中会不断对预报值进行修正,修正过程中,风速波动性减弱,极大值与极小值存在被平滑的迹象。神经网络方法存在容易陷入局部最优、泛化能力易受历史资料影响等不足的特征[24-25]。因此,BP统计订正后风速预报的均值误差将减少,但波动幅度也会减少。应该慎重对待BP神经网络的统计订正,需要兼顾考虑大气的背景场如温度、气压等变化,减少对于风速瞬变特征预报的不足。这也正是作者下一步的工作重点。
