基于匈牙利算法的大井丛井口靶分配设计方法
2022-06-01刘志坤刘成路陈伟林何璟彬王六鹏
刘志坤,刘成路,陈伟林,何璟彬,王六鹏
(1.西安石油大学 石油工程学院,陕西 西安 710065;2.川庆钻探工程有限公司 长庆钻井总公司,陕西 西安 710021)
引 言
近年来,海上油田和陆地油田的开采难度越来越大,大井丛相较于传统单个定向井来说有着诸多优势,被广泛应用于海上钻井平台,它大大减少了钻井成本,满足了油田的整体开发需求,便于油田集中管理,是提高采收率以及增加经济效益的有效手段[1]。而大井丛中设计的井口与靶分别有十几个甚至多达几十个,如何合理将井口与靶逐一匹配,不仅关系到后续的井眼轨道设计,同时若分配不合理则可能导致作业施工难度大,甚至由于钻井轨迹防碰风险大而导致作业失败[2-3]。目前,国内外学者研究方向主要集中在“水平位移和最小”“总井深之和最小”“总井深与总水平位移和最小”这几个方面[4],这些算法计算时间复杂度高,在工程实际应用时难以满足需求。因此,本文提出适用于水平井的最小“水平投影平面特征距离和”的井口靶分配概念,并建立井口靶分配的匈牙利算法模型。
1 井口靶分配问题
在定向井钻井作业中,按目的层油层组数和各组油层连续厚度提供靶点,在油层提供一个靶点,将井口与靶点投影到同一水平面,如图1所示。井口至靶体的水平距离为水平位移,本文将水平位移定义为井口W(X1,Y1)至靶点T(X2,Y2)的直线距离。由水平位移的定义得
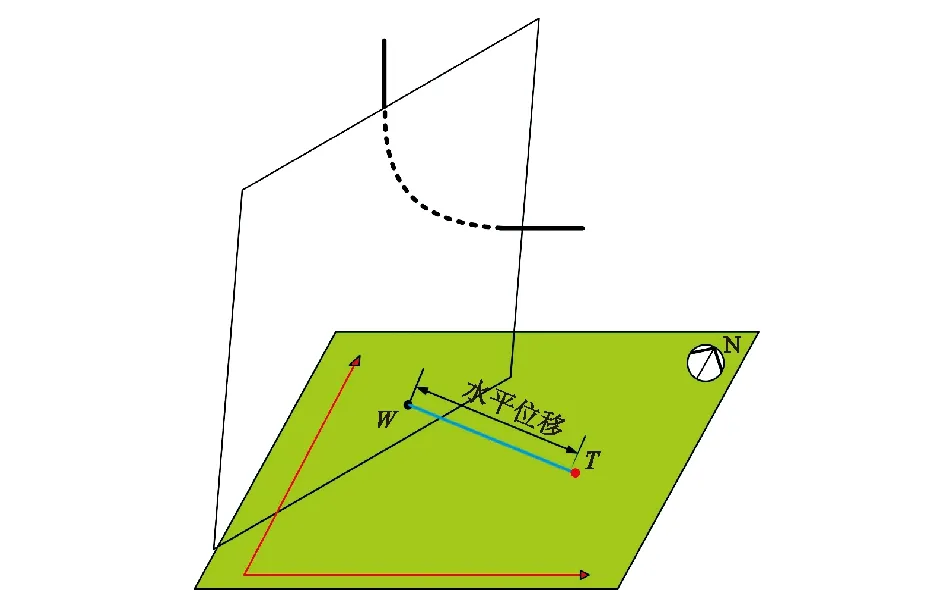
图1 定向井井口-靶点示意图Fig.1 Wellhead-target diagram of directional well
(1)
而涉及到多井口和多靶点的大井丛井场,由于实际井身轨迹与预先设计的井身轨迹之间存在误差,单一的水平位移并不能精确地阐释井口与靶点之间的距离,因此并不适用于实际情况下大井丛的井口靶分配问题。
在大井丛井场中,由于地质因素,井口一般呈n行m列的矩形分布,而水平井的靶段由于地质条件限制通常为沿一个方向平行排列。当井口分布为两列多行,将井口与靶段投影到同一水平面,如图2所示。将水平井靶段T1端到井口W1铅垂线的距离定义为靶前距;井口W1到靶段两端点T1、T2延长线的最短距离定义为偏移距;井口到靶段的水平投影平面特征距离定义为靶前距与偏移距之和。
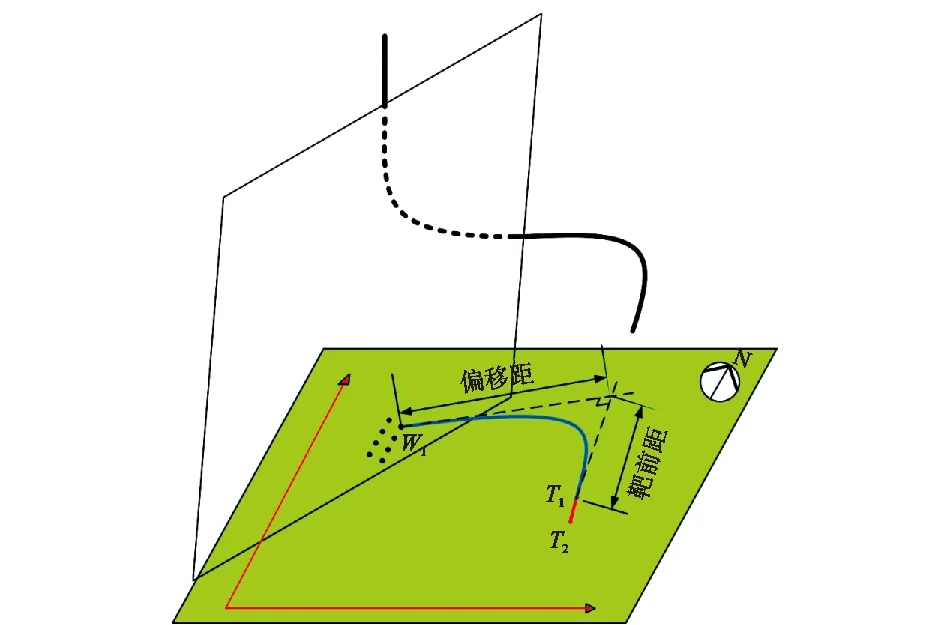
图2 大井丛井口-靶段示意图Fig.2 Wellhead-target diagram of large well cluster
假设水平井口坐标及靶段两端点坐标分别为W1(X1,Y1)、T1(X2,Y2)、T2(X3,Y3),根据靶段两点坐标,建立直线方程
(Y2-Y3)x+(X3-X2)y+(X2Y3-Y2X3)=0。
(2)
根据定义,得到井口与靶段间的偏移距和靶前距[5]
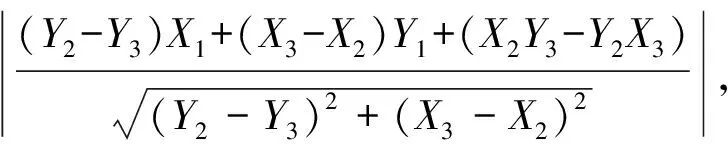
(3)
(4)
2 大井丛井口靶分配优化模型建立
2.1 目标函数
假设n个井口匹配n个靶段,同时规定每个井口只能匹配1个靶段,每个靶段只能由1个井口匹配[6]。依据水平投影平面特征距离定义,可计算出每个井口与每个靶段之间的距离,记第i个井口连接第j个靶段的水平投影平面特征距离为cij>0(i,j=1,2,…,n),则所有井口与靶段之间的水平投影平面特征距离构成的矩阵Cn×n称为距离矩阵[7]。
引入矩阵Xn×n为距离矩阵对应的匹配矩阵,其中每一个元素的取值只能为0或1,当元素值为1时,表示井口与靶段为最优匹配;当元素值为0时,表示井口与靶段不是最优匹配。最终所有的最优匹配构成井口靶段匹配矩阵,根据定义匹配矩阵满足[8]
(5)
则根据最小“水平投影平面特征距离和”的井口与靶段分配原则,可建立最优化数学模型为
(6)
式中:Z为所有井口与靶段间的水平投影平面特征距离和,目标函数是求水平投影平面特征距离和的最小值。
2.2 约束条件
根据定义,井口与靶段之间是一对一匹配的,即井口i只能匹配1个靶段;同理,靶段j只能由1个井口匹配。对于∀i,j=1,2,…,n,目标函数的约束条件为[9]
(7)
该问题属于典型的任务指派问题,即如何指派哪个井口去匹配哪个靶段,反之亦然,使完成所有匹配的总距离最小或者总成本最小,常规优化求解算法并不适用,因此,本文采取匈牙利算法求解[4]。
3 匈牙利算法的井口靶分配实现
匈牙利算法求最优解的基本思想是通过一定的操作将距离矩阵Cn×n的部分元素化为0[10],如果存在一组0,这组0满足:① 0的个数等于矩阵的阶数;②这组0中任意两个0不同行不同列(即独立0元素)[11],那么这组0所对应的分配方式即为最优解[12]。该算法流程图如图3所示。

图3 匈牙利算法流程图Fig.3 Flow chart of Hungarian algorithm
算法具体求解过程:
第一步:遍历每行(列)元素找出每行(列)中最小值,每行(列)所有元素依次减去该行(列)的最小值[13];
第二步:找出只有一个0元素的行(列),标记该0元素,再遍历该0元素所在的列(行),将该列(行)上的其他0元素划掉(表示该靶点或井口已被分配),最终使得每列(行)只有一个0元素(表示单个靶段只能由单个井口匹配)。若标记0元素数目m等于距离矩阵Cn×n阶数n,则已得到该问题的最优解,否则转入第三步[14];
第三步:当m 第四步:找出未被直线覆盖的元素中的最小值,所有未被直线覆盖的元素减去该最小值,被两条线覆盖的元素加上该最小值[16]; 本文实现了大井丛的井口靶分配算法,根据XX油田某大井丛现场数据,现以28口井和28个靶段为例,介绍井口与靶段之间计算分配过程。将井口靶段坐标输入程序中,得出井口与靶段之间水平投影平面特征距离(例:井口W1到靶段T1的水平投影平面特征距离以W1点坐标和A点坐标进行计算),井口与靶段的坐标参数见表1、表2。 表1 井口坐标参数Tab.1 Wellhead coordinate parameters 表2 靶段坐标参数Tab.2 Target coordinate parameters 井口与靶段分配图如图4所示。 图4 井口与靶段分配图Fig.4 Wellhead-target distribution diagram 与文献[2]相比较,本文所采取的匈牙利算法具有较小的时间复杂度,且最大时间复杂度稳定在O(n2),而蚁群算法中考虑蚁群规模和迭代次数时间复杂度为O(n4),本文所提出的算法具有更高的计算效率。 (1)考虑大井丛与定向井的水平井,本文提出了符合大井丛井场实际情况的最小“水平投影平面特征距离和”的井口靶分配概念。 (2)以最小“水平投影平面特征距离和”为目标,并引入井口靶段一对一匹配的约束条件,建立了基于匈牙利算法的大井丛井口靶分配数学模型,能快速高效地得出最优分配结果。通过油田数据实例计算,可以满足现场实际需求。 (3)基于匈牙利算法的井口靶分配数学模型给出的最优结果可能存在钻井轨迹交叉的问题,为了进一步优化该模型,还需要考虑到轨迹防撞方面的问题。
4 实例计算结果

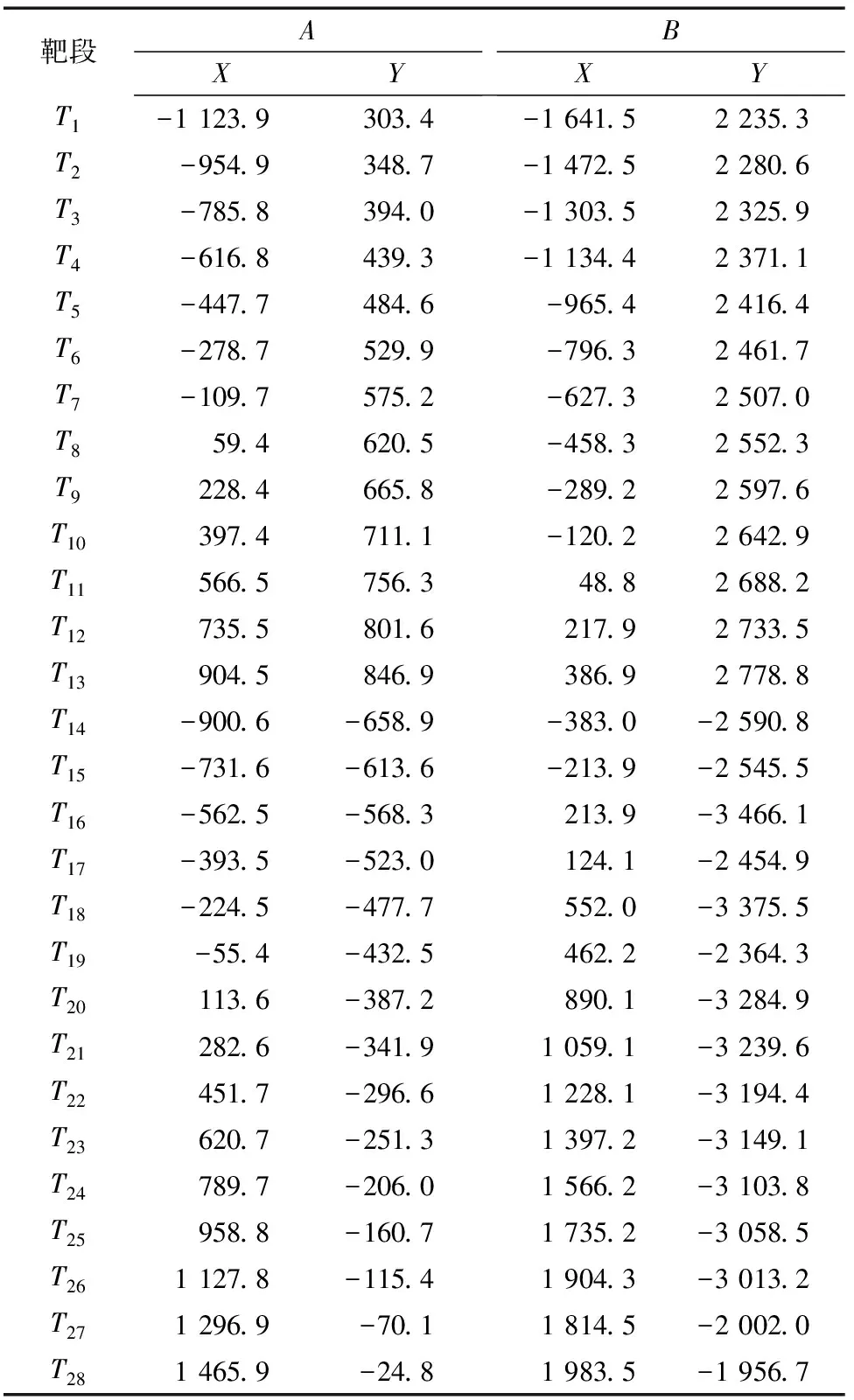
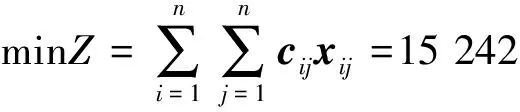
5 结 论
