基于磁声耦合的油水两相流含水率测量结构参数优化

高国旺，赵东亮，武 丹，曲玉龙，王 飞，李元波

(1.西安石油大学 陕西省油气井测控技术重点实验室，陕西 西安 710065；2.中国石油集团川庆钻探工程有限公司 低渗透油气田勘探开发国家工程实验室，陕西 西安 710018；3.青岛大学 电子信息学院，山东 青岛 266071)

引 言

磁声耦合技术是一种基于多物理场耦合思想的新技术，是生物医学工程领域的研究热点[1-2]，但在其他工程领域应用研究较少[3]。磁声耦合技术是通过磁场激励出的声波信号反演出介质电导率分布，故在理论上用于油水两相流电导率测量应是可行的。在磁声耦合油水两相流电导率的测量中，测量结构设计和激励参数非常关键，尤其是激励参数将影响激发出的声信号质量及后续的信号处理。本文借鉴磁声耦合技术在生物医学领域的应用，对磁声耦合技术测量油水两相流电导率中的机理进行研究，进一步论证磁声耦合测量油水两相流电导率的可行性；并对测量结构与激励参数进行仿真分析，为后续的实验研究和实际应用奠定基础。

1 磁声耦合工作原理

对置于稳恒磁场的导电介质，施加同方向的交变磁场，在电磁感应作用下，介质内感生出涡流，涡流受到洛伦兹力的作用，产生瞬间的位移，形成声波振动，振动的频率与外加脉冲磁场频率相同[1，3]。此时，利用声换能器可以接收与介质的电导率分布有关的声信号[4]。借鉴前人提到的正逆思想，声信号中包含如电导率在内的电特性信息，在检测到磁声信号之后，反推求解电导率的过程属于磁声耦合研究的逆问题[5]。

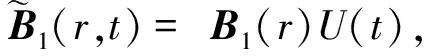
∇×(J/σ)=(∇×J)/σ+∇(1/σ)×J=-B1。

(1)

通过声波反演后得到目标体内的电导率为：

(2)

根据矢量运算法则有：

∇(J×B0)=(∇×J)B0-J∇×B0。

(3)

B0由外部源产生，∇×B0=0，因此，求解电导率的公式可以进一步化简为：

(4)

式中：B为磁感应强度，T；E为电场强度，N/C；U为电位，V；J为电流密度，A/m3；σ为电导率，S/m。

由于油和水的电导率差异巨大，不同含水率下的油水两相流电导率也有很大的变化，假设油、水两相均匀混合，则混相电导率、含水率及水的电导率之间的关系可用Maxwell公式描述：

(5)

式中：ρ为含水率；σm、σw分别为两相流和水的电导率。

根据上述原理可知，磁声耦合油水两相流电导率的测量是在声换能器检测到的声波信号后得到油水两相流的电导率信息，再根据电导率与含水率的关系得到油水两相流含水率。

2 结构模型与仿真分析

2.1 仿真模型构建

在COMSOL Multiphysics 5.4中加载ACDC-磁场(mf)模块，选择频域研究步骤[7]，建立如图1所示的仿真模型图。其中包括圆环状线圈、圆柱形管道、静磁铁以及空气背景；仿真模型中，激励线圈置于管道的正上方，通入顺时针方向的正弦电流后产生交变磁场，产生的交变磁场方向为从上指向下；激励线圈和管道共置于上下两块静磁铁产生的静磁场当中，静磁场N级在上、S级在下，磁场方向由N级指向S级。

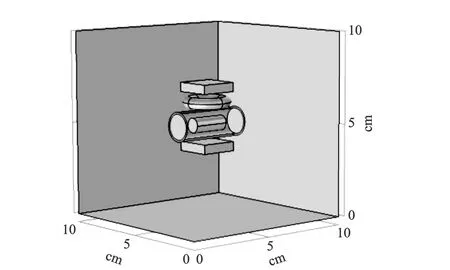
图1 仿真模型图Fig.1 Simulation model diagram

2.2 静磁场参数优化

静磁场参数的优化主要为两块静磁铁之间的距离优化，目的是产生强大且稳定的稳恒磁场。静磁铁相对位置如图1所示，设置静磁场为0.4 T[8]，磁铁的尺寸为30 mm×30 mm×10 mm；改变两块静磁铁之间的距离，观察其间的磁通密度变化情况，如图2所示，静磁铁间距离越近，其间的磁通密度模越大且越接近于稳恒磁场，故后续的仿真模型搭建时应在满足工况的条件下选择距离最近的静磁铁位置，以保证产生良好的稳恒磁场。

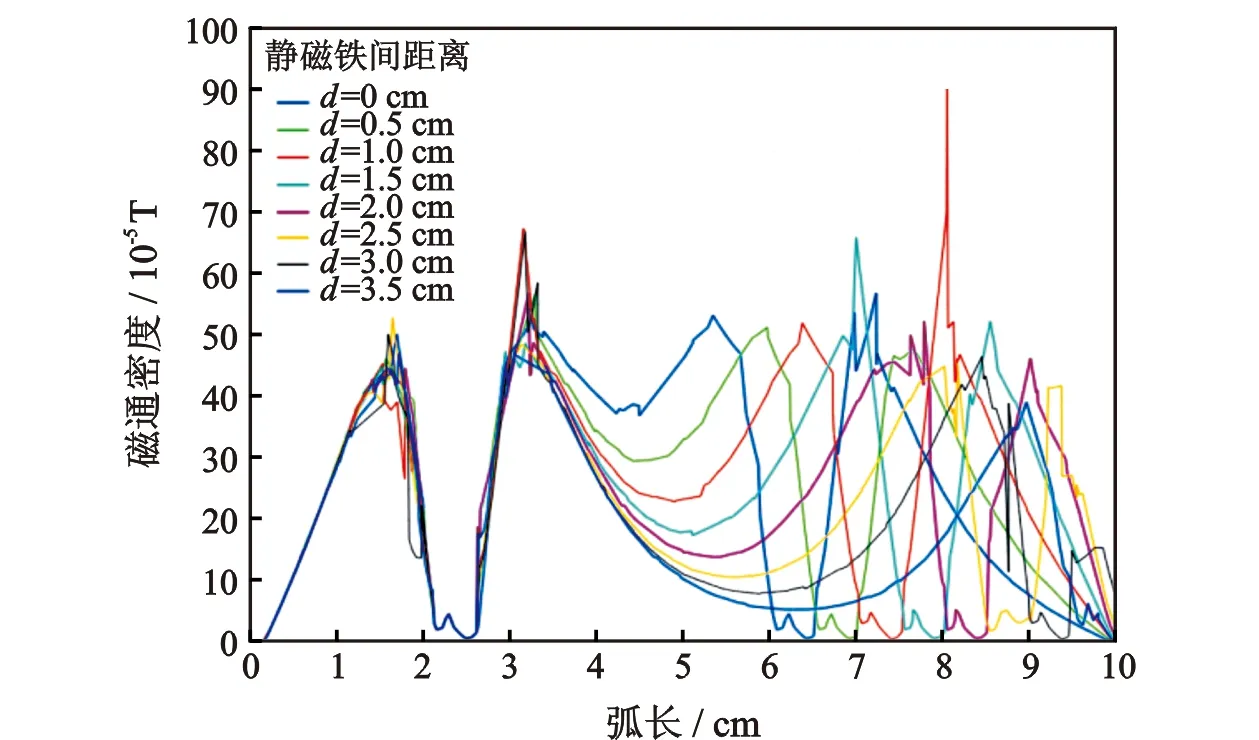
图2 静磁铁间距与磁通密度的关系Fig.2 Relationship between static magnet spacing and magnetic flux density

2.3 激励电流频率优化

基于图1所示仿真模型，向线圈中通入频率不同、大小为1 A的正弦交流电，分别在频率为10 kHz、100 kHz、1 MHz和1.5 MHz下分析一条平行穿过管道中心的截线，其上的磁通密度(x分量)如图3所示，可知在4种频率下，管道内的磁通密度几乎无变化；其上的感应电流密度(y分量)如图4所示，可知在4种频率下，截线上的感应电流密度随频率的增大而增大，且变化明显。

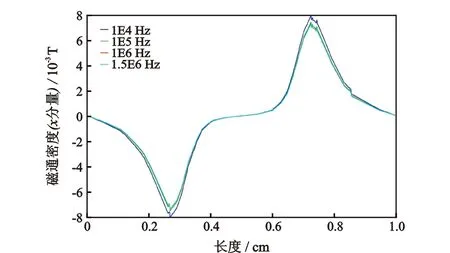
图3 不同频率下管内磁通密度Fig.3 Magnetic flux density in tube at different frequencies

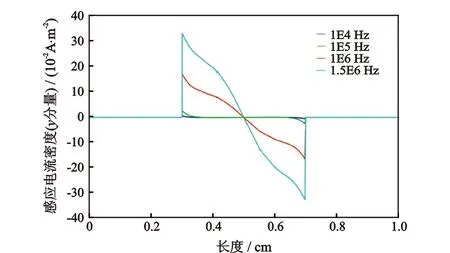
图4 不同频率下管内感应电流密度Fig.4 Induced current density in tube at different frequencies

根据磁声耦合成像原理可知，洛伦兹力作用所产生的振动与声波和激励线圈注入的交流电频率相同[4]；后续实验平台搭建时欲选用Panametrics V303水浸式传感器作为超声换能器，其中心频率为1 MHz。根据上述仿真分析并结合用于声波检测的超声换能器选型，选择1 MHz作为激励电流的频率。

2.4 线圈位置优化

基于图1仿真模型中所示的线圈模型进行仿真，向线圈内通入大小为1 A，频率为1 MHz的交变电流后，线圈在空气背景域中产生的磁场分布如图5所示，箭头表示磁通密度x，y，z分量，此处对箭头进行对数处理，以便于更加清楚地表示磁场大小和方向，其长短代表磁通密度的大小。从结果来看，磁力线穿过线圈呈对称分布，线圈附近区域磁场场强较强，远离线圈的区域磁场场强较弱。

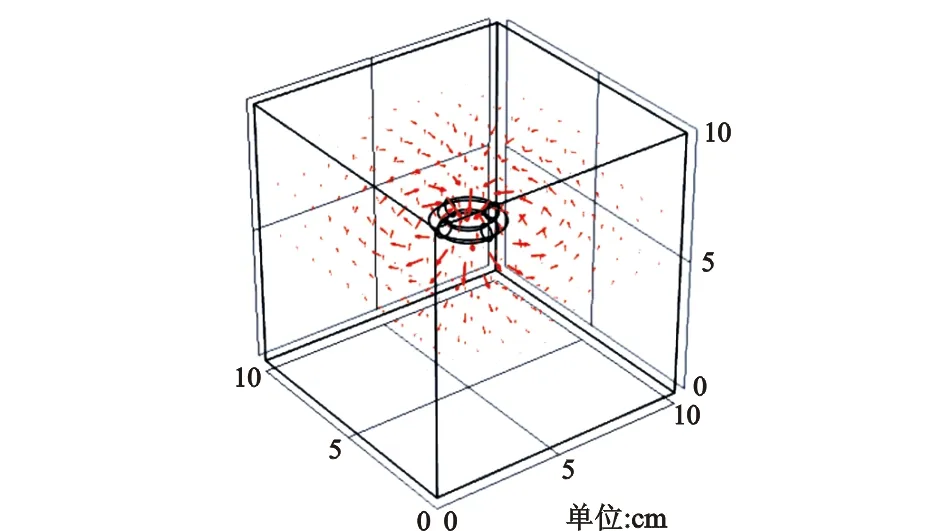
图5 激励线圈磁场分布Fig.5 Magnetic field distribution of excitation coil

综上分析，在仿真模型和实际实验平台搭建时，应将被测物件置于激励线圈的正下方，与被测物件的距离越近越有利于实验分析。

2.5 线圈匝数优化

基于图1的模型，采用参数化扫描的方法改变线圈匝数，得到频率为1 MHz、电流大小为1 A、匝数分别为1 000、2 000、3 000、4 000匝时，平行穿过管道中心的三维截线上的磁通密度。图6所示随着线圈匝数的增加，管道内的磁通密度也在增大；图7所示是随着线圈匝数的增加，线圈内部电感的变化情况，根据经验公式，线圈电感量与线圈匝数成正比。

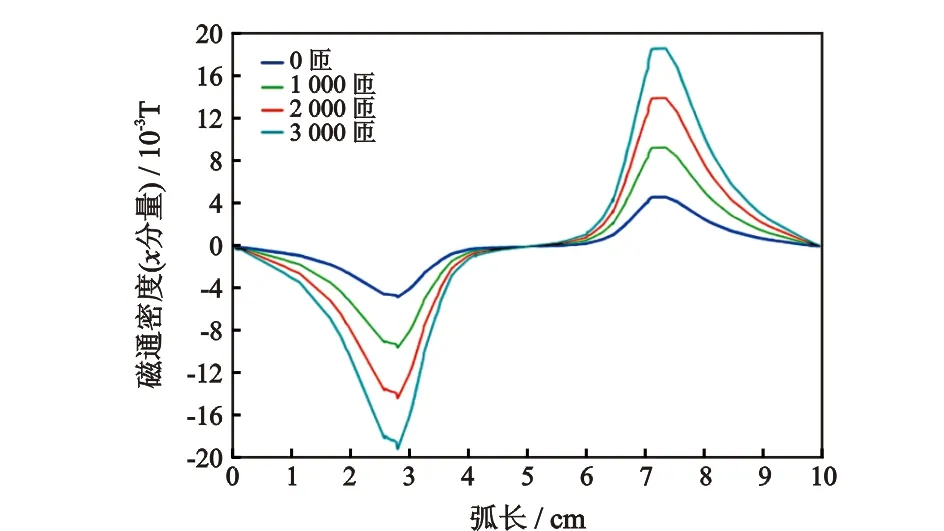
图6 线圈导线匝数对磁通密度的影响Fig.6 Effect of coil turns on magnetic flux density

线圈对交流电有电抗，其作用跟电阻相似，在不考虑直流电阻的情况下，假设电流频率一定、线圈匝数增加，线圈电感量必然增大，对交流电的感抗也会随之变大，感抗对交流电流的阻碍作用也越大，因此电流必然下降[9]。介于电感线圈“通低频、阻高频”的电特性和实验的实际需求，最终选定线圈匝数为2 742匝作为折中方案。

3 结果与分析

基于图1的仿真模型和上述参数优化，在管道中分别加入纯水和纯油进行仿真，观察在纯水和纯油两种工况下，一条平行穿过管道中心处的三维截线上的感应电流密度，以此来分析在两种情况下管道内感应电流分布情况，下管道内感应电流分布情况如图8、图9所示。

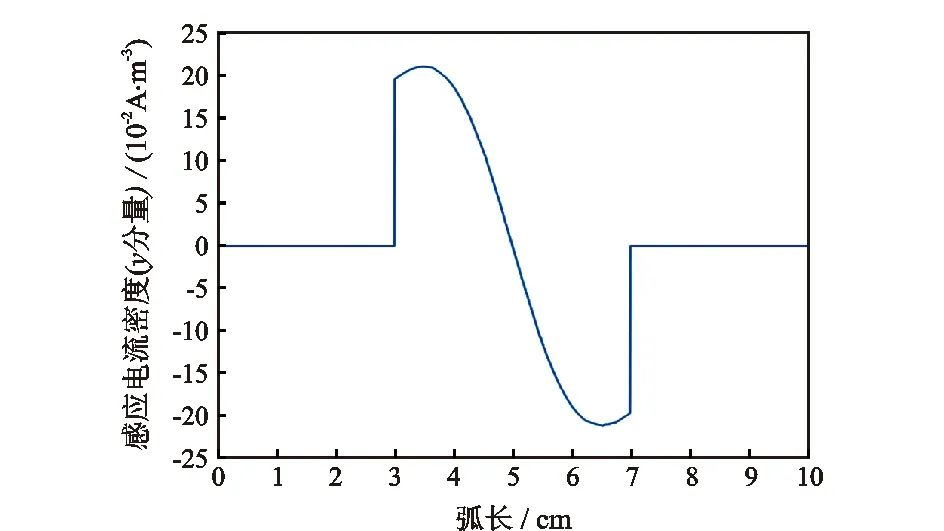
图9 管道内感应电流密度(纯油)Fig.9 Induced current density in tube ( pure oil)

由于纯水和纯油电导率的差异，两者的感应电流密度也有着数量级上的差异，可以预见同样的数量级差异会反映在洛伦兹力中。

在仿真模型管道中模拟水包油的情况，如仿真模型图1所示，管道中的小圆柱体代表油，其余部分代表水。感应电流分布情况如图10所示，分析可得，由于空气域电导率无限小，无感应电流存在；原油电导率极低，仅有极其微弱的感应电流存在；而水域由于电导率较大，存在明显的感应电流分布。

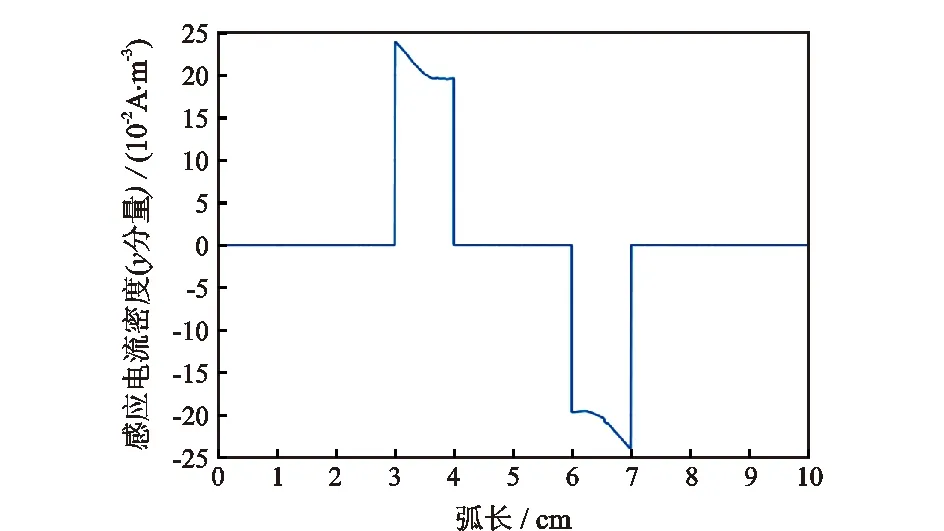
图10 管道内感应电流密度(水包油)Fig.10 Induced current density in tube ( oil-in-water)

感应电流在稳恒磁场中产生洛伦兹力，洛伦兹力的大小与感应电流的大小成正比。在仿真模型中分别将装有纯水、纯油和水包油的管道置于稳恒磁场之中，向激励线圈中通入频率为1 MHz、大小为1 A的交流电，平行穿过管道中心的三维截线上的洛伦兹力分布如图11所示。通过观察，洛伦兹力分布可以与图10电流分布相对应，在空气域中没有感应电流也即没有洛伦兹力的存在；油中有感应电流存在但量级很小，故油中也只有很少的洛伦兹力存在，几乎可以忽略不计；水中的感应电流较多，故水中有明显的洛伦兹力存在。

通过三维截线上的洛伦兹力可以看出，截线上分布有2 cm的油和2 cm的水。接下来按照极限的数学思想，如果将这一条截线放大到与管道一样粗，将观察范围从三维截线扩大到三维圆柱体之中，通过软件中的体积分计算可以得出管内洛伦兹力的体积分，可以更加直观地观察到纯水、纯油和水包油情况下管内整体洛伦兹力情况(表1)，纯水的洛伦兹力最强，纯油的最弱，水包油的介于纯油和纯水之间。

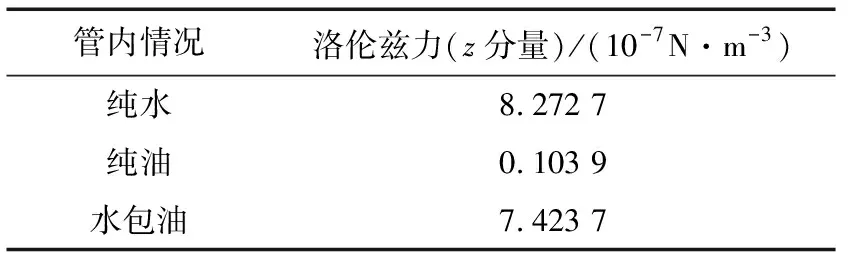
表1 管内洛伦兹力分布Tab.1 Lorentz force distribution in tube

通过改变管道内水包油中油块的大小，亦即改变管道内含水率的大小。随着含水率的变化， 管道内的洛伦兹力在纯油和纯水之间有规律变化，并且洛伦兹力和含水率成一定程度上的正比关系，如图12所示。可以通过检测管道内油水混合物的洛伦兹力来推断出管内油水两相流的含水率。介质内部的涡流受到洛伦兹力的作用，产生瞬间的位移，从而形成与外加交变磁场频率相同的声波振动[10]，因此可以得出，声波信号也与两相流含水率之间存在类似的关系。

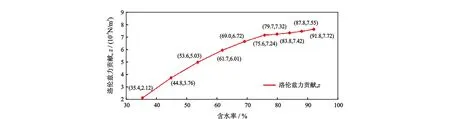
图12 洛伦兹力与含水率的关系Fig.12 Relationship between Lorentz force and water cut

4 结 语

本文对磁声耦合测量油水两相流含水率模型进行了仿真和参数优化，确定了仿真模型结构和激励参数，为后续的声信号采集和声信号处理奠定了数据基础。研究结果说明在磁声耦合作用下，管道中的洛伦兹力大小与油水两相流含水率之间成正比关系，即管道中的洛伦兹力越大，油水两相流含水率越高；介质中带电粒子受洛伦兹力作用产生位移振动，从而产生声波信号，洛伦兹力的大小可以反映出声波振动的大小，因此从声换能器检测到的声波信号大小也可得出油水两相流的含水率。