正弦荷载和列车荷载下地铁环境振动减振措施数值模拟研究
2022-06-01李旭东1马笑遇1叶海坪2波3刘德声袁宗浩
李旭东1,马笑遇1,叶海坪2,俞 波3,刘德声,袁宗浩
(1.杭州地铁开发有限公司,浙江 杭州 310021;2.杭州西誉置业有限公司,浙江 杭州 310024;3.宏润建设集团股份有限公司,浙江 杭州 310000;4.浙江工业大学 土木工程学院,浙江 杭州 310023)
随着地下铁路的飞速发展,地铁运营带来的一系列问题逐渐显现出来。地铁运营时车轮与轨道间存在的相互作用会产生振动,该振动会通过隧道和周围的土,以波的形式向附近建筑物传播,产生噪音和振感。这种振动可能会使敏感的设备和器材出现故障,不仅影响地铁沿线建筑物的安全性,而且给附近居民的生活带来很大的困扰[1]。国内外专家学者经过多年的探讨,研究出一系列地铁振动模拟方法及数值分析模型。Chua等[2]建立了一个地铁-土-结构相互作用的二维有限元模型。Nejati等[3-4]建立了二维有限差分预测模型来研究环境振动问题。Jones等[5]建立了一种利用薄层法模拟半无限层状土壤的二维预测模型。Godinho等[6]提出频域耦合模型,并采用有限元法和基本解法求解土-结构相互作用问题。Yang等[7]用2.5维有限元法研究了地下列车引起的地面振动。Sheng等[8]提出了一个通用的2.5维有限元-边界元模型来分析隧道中铁路交通引起的地面振动,其中2.5维边界元模型用于土体,2.5维有限元模型用于隧道结构。Francois等[9]和Galvin等[10]引入了2.5维的正则化边界积分方程和基于层状半空间格林函数的边界元模型,该模型在分层半空间的情况下不需要对自由界面和层间界面进行离散化。
笔者对地铁列车运行引起的环境振动以及减振措施进行研究。首先,通过选择合理的模型与材料参数,建立一个有限元-无限元隧道-土耦合模型,采用正弦荷载和列车荷载激励地基土体来研究移动列车荷载下空沟及填充沟的减隔振效果,由于任何复杂的荷载形式均可以写成正弦荷载的叠加形式,不同频率的正弦荷载可以分频段研究空沟和填充沟的减振效果;然后,在此定性分析的基础上,进一步定量分析实际移动列车激励下空沟、填充沟的减隔振效果,在模型中采用单位正弦荷载进行激励,分析了路径减振措施填充沟在不同荷载频率、填充沟距离振源不同距离、填充沟不同深度等因素对该措施减振效果的影响;最后,研究填充沟在实际列车荷载下的减振效果,通过现场振动实测获得钢轨加速度,求解上部车体竖向运动平衡方程,获得施加在轨道结构上的实际轮轨动力作用力,并输入至有限元模型中,从而研究实际地下列车荷载激励下填充沟减振措施的减振效果。
1 有限元模型的建立
1.1 基本假设
地铁振动荷载下土的应变幅值在10-6~10-4及以下的范围可以将土的变形性质看作弹性形变,在应变较小时,可以认为土体没有产生塑性形变,即此时可以认为土体为线弹性材料。因此,作出如下假设:
1) 模型中均为各向同性的材料。
2) 假定土体为均质土层,不考虑土体孔隙比及地下水的存在。
3) 假定笔者研究的动力问题为线弹性问题。
1.2 模型尺寸与单元尺寸
在有限元问题的分析过程中,模型尺寸和单元尺寸的选择十分重要。如果模型选择的过小,则会由于边界反射等问题的存在使最终模拟的结果产生很大的影响;如果模型选择的很大,虽然可以很好地模拟实际情况,满足计算精度,但是会导致过多的单元被划分出来,计算量变得难以接受。同时,若单元尺寸选择不当,则会产生频散效应和低通效应。因此,选择一个合理的模型参数尤为重要。经试算,所用模型深度取70 m,宽度取120 m;模型单元尺寸在近振源区域,取0.2 m,远振源区域取1 m。建立的有限元模型如图1所示。

图1 二维有限元-无限元隧道-土模型Fig.1 Two-dimensional finite element-infinite element tunnel-soil model
由于大地是无穷域,而有限元法只能离散有限区域,因此在模型边界底部和侧面添加了无限元,从而使得外行能量得以逸散,防止波动反射的发生。图1中间部分为有限元区域,靠近隧道6 m×6 m范围为网格加密区,尺寸为0.2 m,远振源区为网格尺寸为1 m,设置外围无限元边界来减少波在边界的反射。
1.3 场地参数的确定
在二维有限元-无限元隧道-土模型,考虑各材料都为均质体,设置了两种不同性质的材料,分别为地基土和混凝土(模拟隧道衬砌),材料参数如表1所示。由表1可知:在这些动力因素存在时考虑土的变形和强度问题需要考虑到瞬时性和反复性这两个特点,用土体的动参数(表1中的动弹性模量和动阻尼比)来替代静载状态下土体的参数。

表1 模型材料参数Table 1 Material parameters of the model
1.4 阻尼参数的选取
模型采用瑞利阻尼,系数α和β的计算式为
(1)
(2)
式中:ξi为i振型的阻尼比;ωi为i振型的圆频率;ωj为j振型的圆频率。
假定已知频率为10 Hz和80 Hz的阻尼比,从而可推得α=3.351和β=0.000 106 1,土的阻尼系数计算式为
(3)
(4)
式中:ξi为第i振型的阻尼比;ωi为第i振型的圆频率;ωj为第j振型的圆频率。
将α和β代入式(2~4),可得到频率为10~80 Hz的阻尼比,阻尼比随频率变化情况如图2所示。
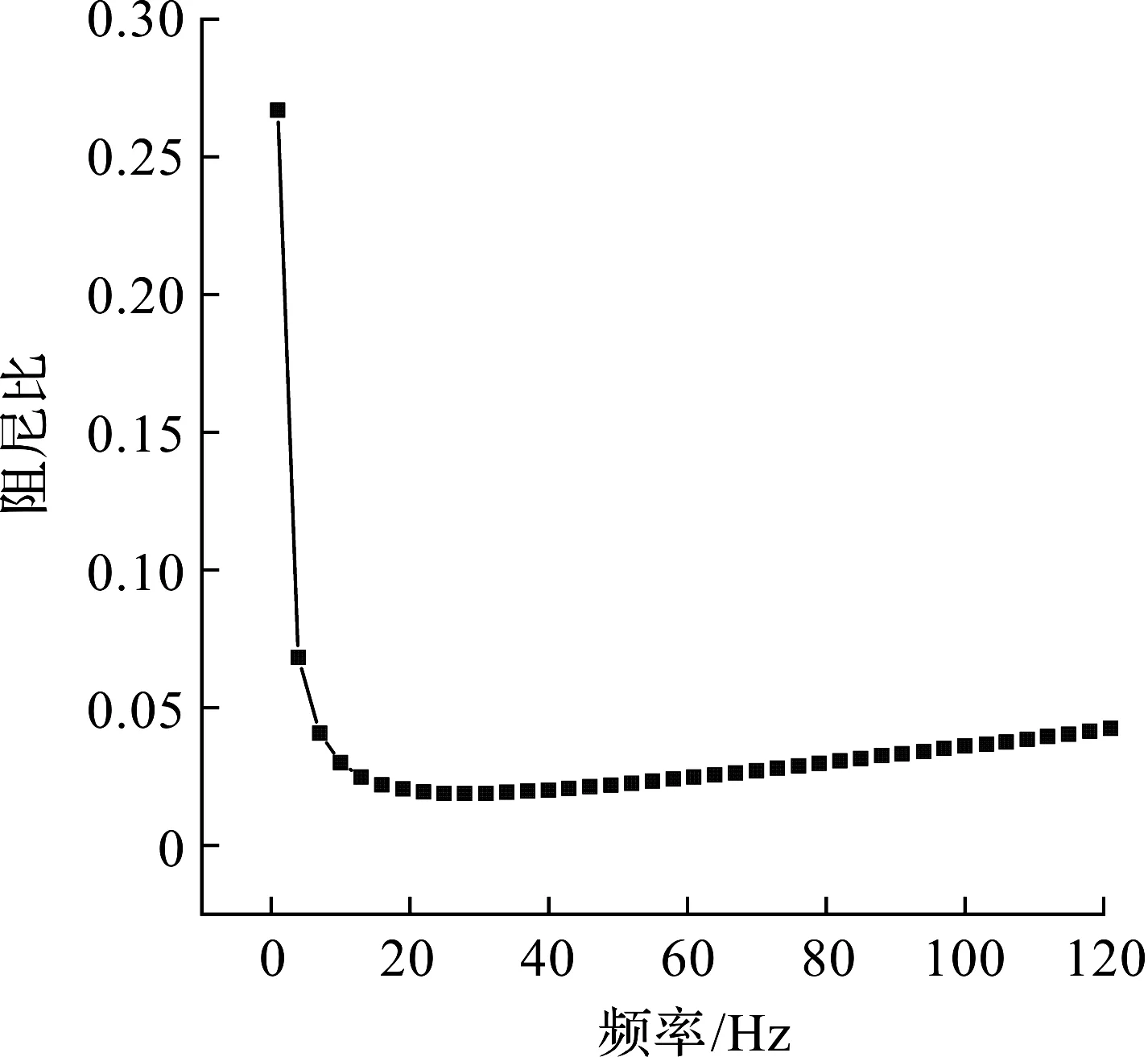
图2 阻尼比随频率变化图Fig.2 The damping ratio versus the load frequency
2 模型验证
因为研究模型关于对称轴对称,所以采用一半的模型计算。为了验证模型的正确性,建立了一个二维模型,土体的各项参数取值参照Ahmad[11]的研究:地表瑞利波波速为250 m/s,土体重度为17.5 kN/m3。地表处施加频率为50 Hz的荷载。文献[11]采用边界元方法计算了无沟工况下A点(距离振源25 m)后的地表归一化位移幅值。通过ABAQUS模型模拟所得结果和该文献的结果对比如图3所示。
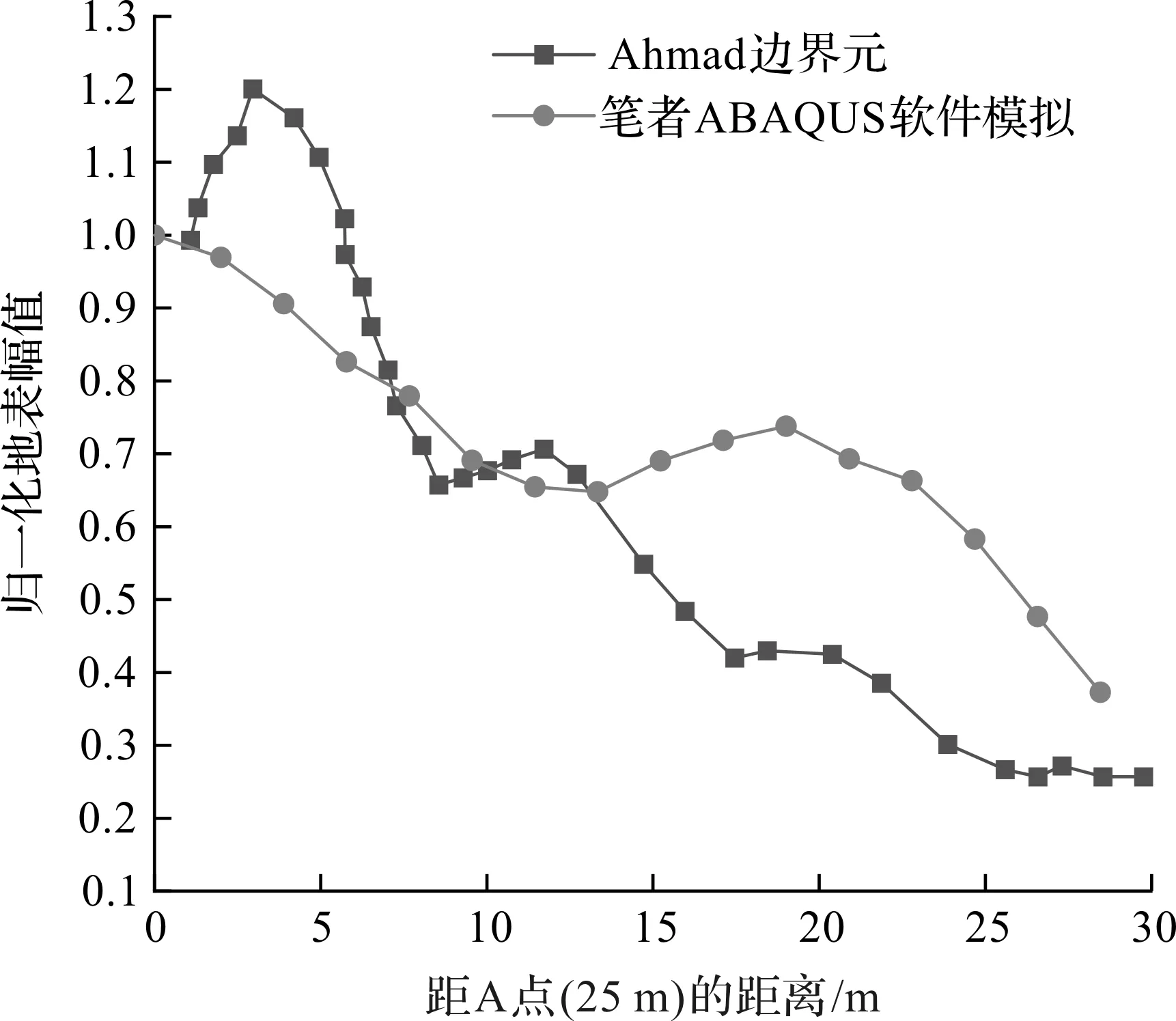
图3 模型验证结果对比图Fig.3 Verification of the present model
由图3可知:因为参考文献[11]中没有给出瑞利阻尼具体数值,所以用ABAQUS模型得到结果和参考文献未完全吻合,但可以看出结果曲线的变化趋势和数量级与参考文献[11]的趋势大致相同。
3 点荷载作用下屏障减振效果分析
为分析点荷载和移动列车荷载下空沟屏障和填充沟屏障的减振效果,分别针对这两种工况进行数值模拟分析。
3.1 空沟屏障隔振分析
3.1.1 不同频率下空沟隔振效果
在距离振源处6 m布设宽度为3 m,深度为16 m的空沟,计算模型如图4所示。

图4 工况1计算模型图Fig.4 Computational model of case 1
在地表距离振源不同的距离选取观测点,通过在有沟和无沟两个计算模型,分别在仰拱处作用频率为10,20,40,80 Hz的正弦单位力,得到地表加速度响应,如图5所示。由图5可知:振动波的频率越高,其在土体中传播时衰减越快。在设置了空沟以后,沟后地表的振动响应明显地产生了衰减。同时可以发现,距离空沟50 m以后隔振效果比较差。计算结果表明空沟的近场隔振效果优于远场隔振效果。需要说明的是:在荷载频率分别为20,40 Hz时,存在多处振动放大的现象,加设空沟会使沟前地表振动加速度水平升高。这是由于:一方面,振动能量在经过隔振沟前会产生堆积效应,沟越深,在沟前堆积的能量也会越多;另一方面,波在空沟处产生反射,从而使振动响应在沟前增加。
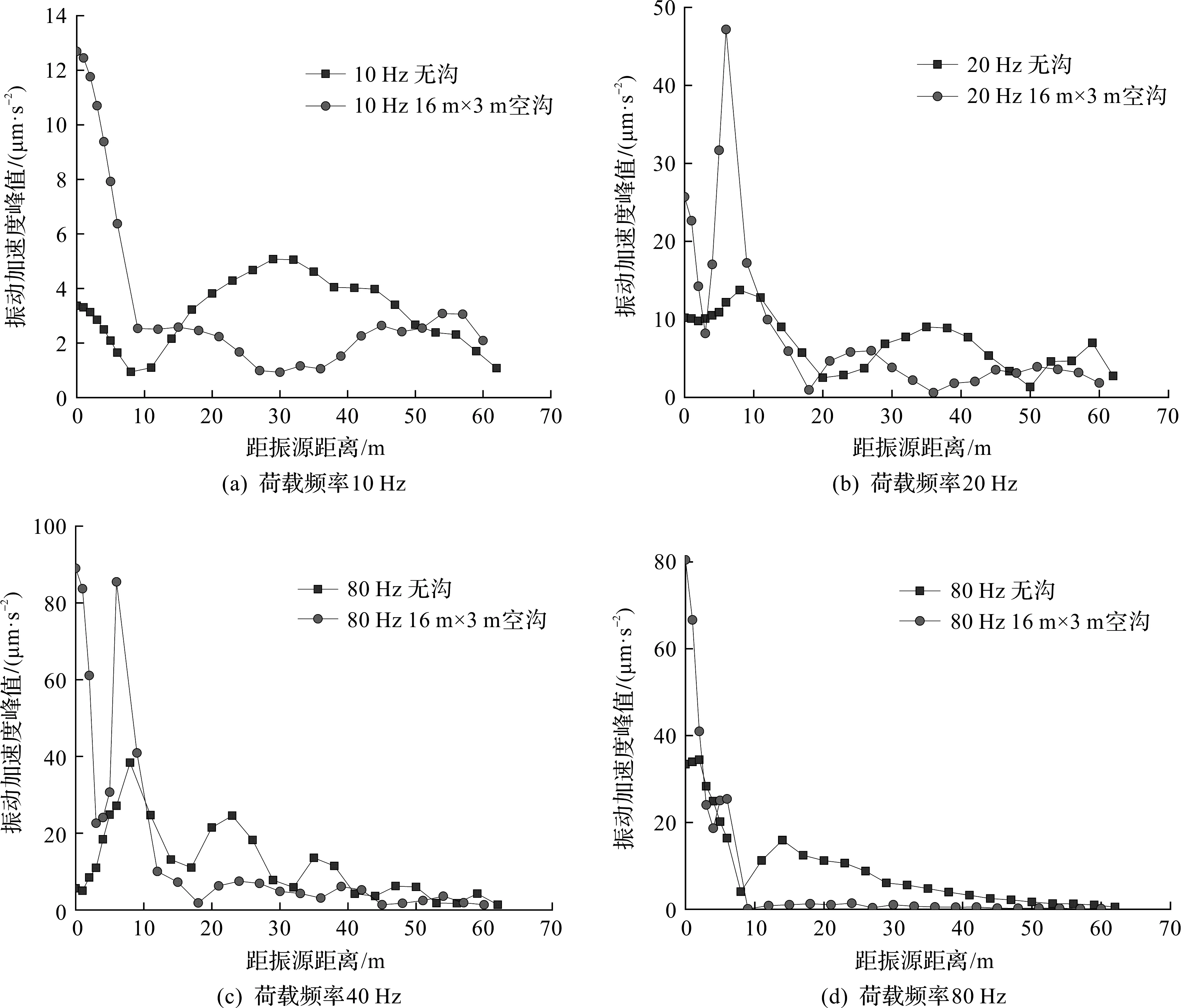
图5 不同振动频率荷载的隔振效果对比Fig.5 Vibration isolation effect for different load frequencies
3.1.2 空沟深度对隔振效果的影响
由于交通荷载引起的环境振动频率范围多在10~80 Hz,而阻尼值具有频率依赖性,为使所选的阻尼值具有较好的频率适用性,选取10 Hz单位正弦荷载作为低频振源和80 Hz单位正弦荷载作为高频振源开展进一步研究。在所建立二维有限元-无限元隧道-土模型中,固定隧道埋深10 m,在离振源水平距离12 m处设置宽度为2 m,深度分别为8,12,16 m的空沟,分别对其施加上述两种频率的荷载,结果如6图所示。
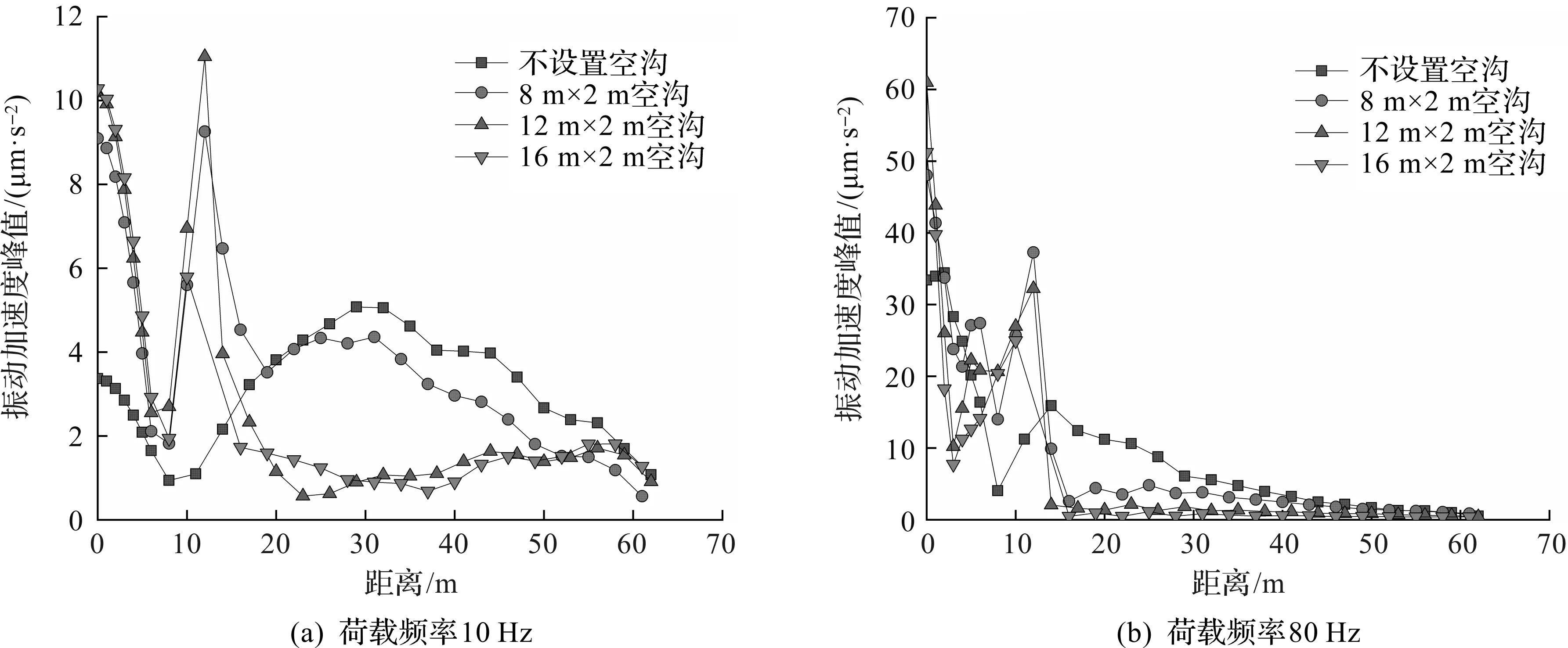
图6 不同深度空沟对低、高频荷载的隔振效果对比Fig.6 Vibration isolation effects of empty trench with different depths for low and high load frequency
由图6可知:空沟的深度对隔振效果的影响很大,空沟越深,其隔振效果越好。当沟深增加到16 m时,隔振效果显著增加。通过对比10 Hz低频荷载和80 Hz高频荷载可以发现,空沟对高频荷载的隔振效果更好,其中使用8 m空沟其隔振效果已较优,进一步增加沟深对其减振效果影响不大;反观10 Hz低频荷载,使用8 m空沟隔振效果并不是很好,需要增加空沟深度才能达到比较好的隔振效果。
3.1.3 空沟位置对隔振效果的影响
空沟距离振源分别为6,10,14 m。其中6 m空沟表示主动隔振(空沟距离振源较近),14 m空沟表示被动隔振(空沟距离振源较远),10 m为对照组。在所建立的模型中,固定隧道埋深10 m,空沟宽度为2 m,深度分别为12 m,结果如图7所示。
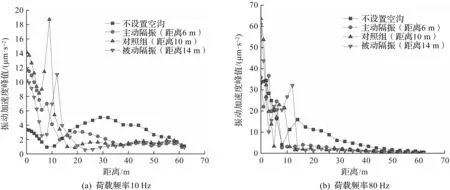
图7 不同距离空沟隔振效果对比Fig.7 Vibration isolation effects for different spatial distance of the empty trench to the vibrating source
由图7可知:对于不同位置的空沟,沟距离振源越近,振动越早衰减。对于频率为10 Hz的荷载,隔振效果随着空沟到振源的距离增加而变好,而随着荷载频率增大,振动在土体的衰减变快,空沟距离对隔振效果的影响变得不明显。可以看出:主动隔振措施虽然可以更早地起到隔振作用,但是对于低频荷载的隔振效果没有被动隔振效果好。
3.2 填充沟屏障隔振分析
虽然空沟隔振措施有着十分重要的意义,但是空沟在实际施工中也存在很多问题,例如施工中可能会发生塌孔,地下水位过高也不适用;同时空沟的支护以及维修也需要投入较大的成本,因此空沟在地铁振动减振措施中并不是一个最好的选择。而解决该问题的一个方法就是在开挖的空沟中填充不同材料形成填充沟进行隔振。笔者将对不同填充材料的填充沟屏障隔振性能进行研究。
陈功奇等[12]对地表列车荷载作用下填充沟的隔振性能进行了研究。参照文献[12]的填充沟材料参数,选择混凝土、细砂、橡胶和泡沫4种不同刚度的填充材料进行研究,填充沟距离振源9 m,深度为12 m。填充材料的计算参数如表2所示,模型计算结果如图8所示。
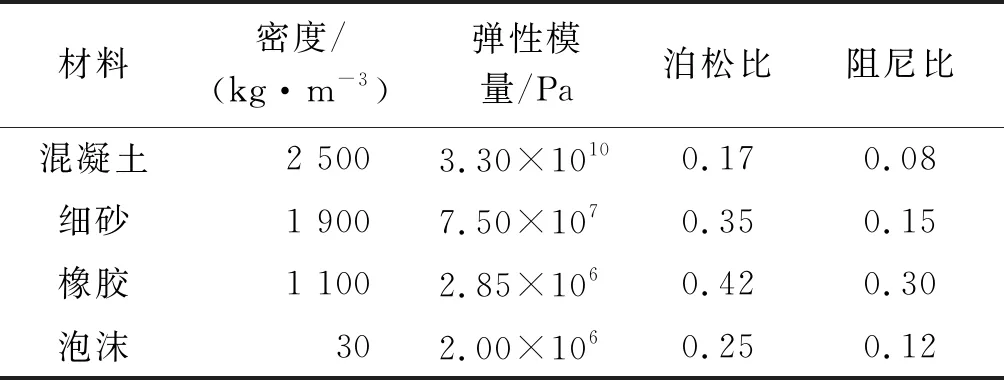
表2 填充材料参数Table 2 Filling material parameters
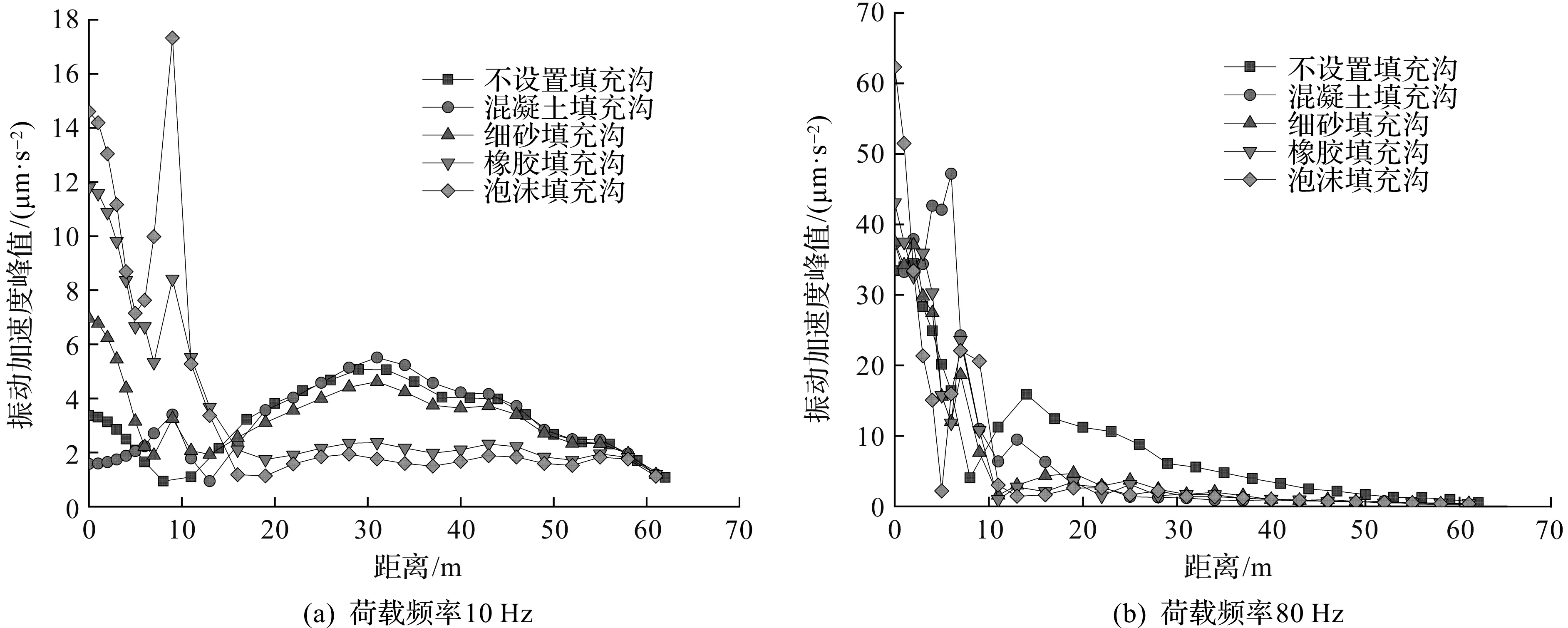
图8 不同填充材料的填充沟隔振效果对比Fig.8 Vibration isolation effects of different filling materials on low and high frequency loads
由表2和图8可知:橡胶和泡沫的隔振性能明显优于细砂和混凝土。由此可以得到一个结论:填充沟隔振材料的材料刚度是影响隔振效果的关键因素之一,隔振材料刚度越小,其隔振性能越好。因此,当填充材料的刚度为0,即填充沟变为空沟时,其隔振性能最好。10 Hz正弦荷载作用下相同深度填充沟和空沟的隔振效果对比情况如图9所示。
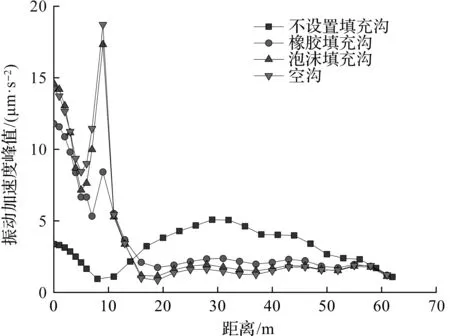
图9 荷载频率为10 Hz的空沟与填充沟隔振效果对比图Fig.9 The comparison diagram of vibration isolation effect between empty trench and filled trench with load frequency of 10 Hz
由图9可知:空沟的隔振效果优于填充沟。但是在实际工程中,空沟会受到建筑物附近土层的限制,水位较高时不适用,开挖的深度不能太深,施工成本过高,而且需要对其加以支护防止坍塌,因此空沟的应用会受到很多因素的制约。在施工过程中,可以改用填充沟来代替空沟,在设计填充沟时,填充材料应尽量选取刚度较小、松软的材料,以获得较好的隔振效果。
4 地铁列车荷载隔振措施效果分析
在上述研究过程中,对模型施加的荷载设定为固定频率的正弦荷载,即只针对了某一特定频率对隔振沟的隔振效果进行研究。实际上,单一频率的简谐荷载只能反映荷载的某种振动特性,不能反映出真实的地铁列车运行情况。因此,对隔振沟在地铁实测列车荷载作用下的隔振效果进行分析。
4.1 实测轮轨力
在地铁振动测试中,可以较容易地采集到轨道某一点处的位移响应,但是对于轮轨力的获得却比较困难。笔者将阐述如何通过实测的钢轨振速获取轮轨间作用力。
孙晓静[13]将地铁列车转化为一系列二系弹簧质量模型,通过建立每一个刚体的动力平衡方程可以获得相应的位移量与力的关系,模型如图10所示。
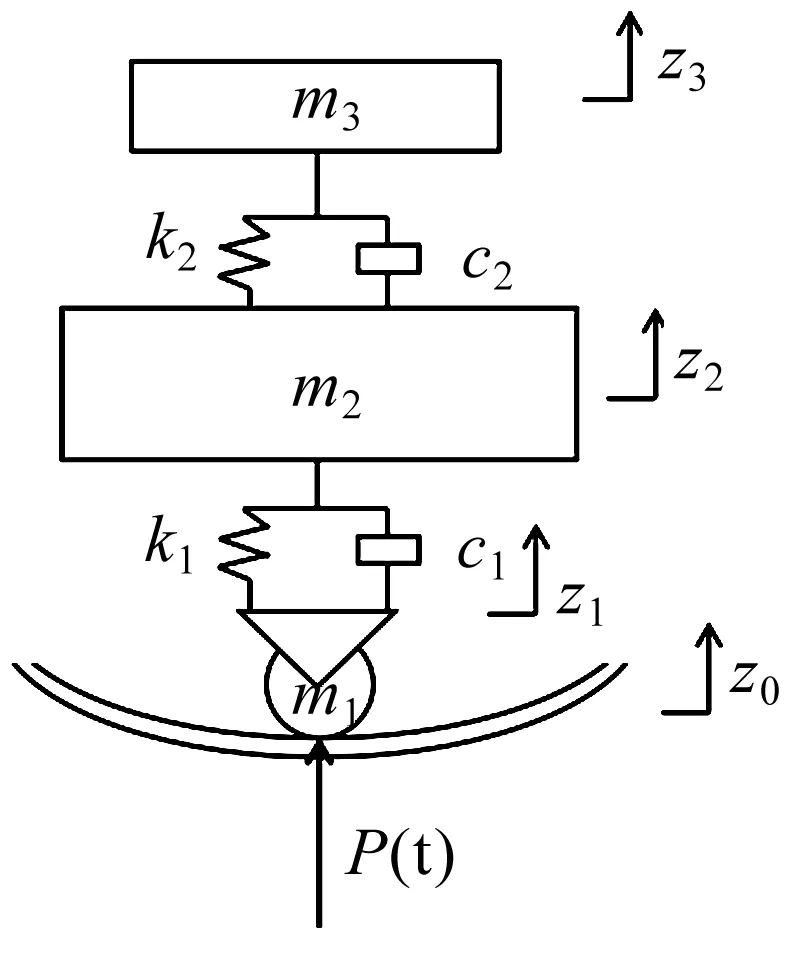
图10 二系弹簧质量模型Fig.10 Mass model of secondary spring
钢轨振动实测在杭州某车辆基地开展,地铁列车模型参数的取值如表3所示。
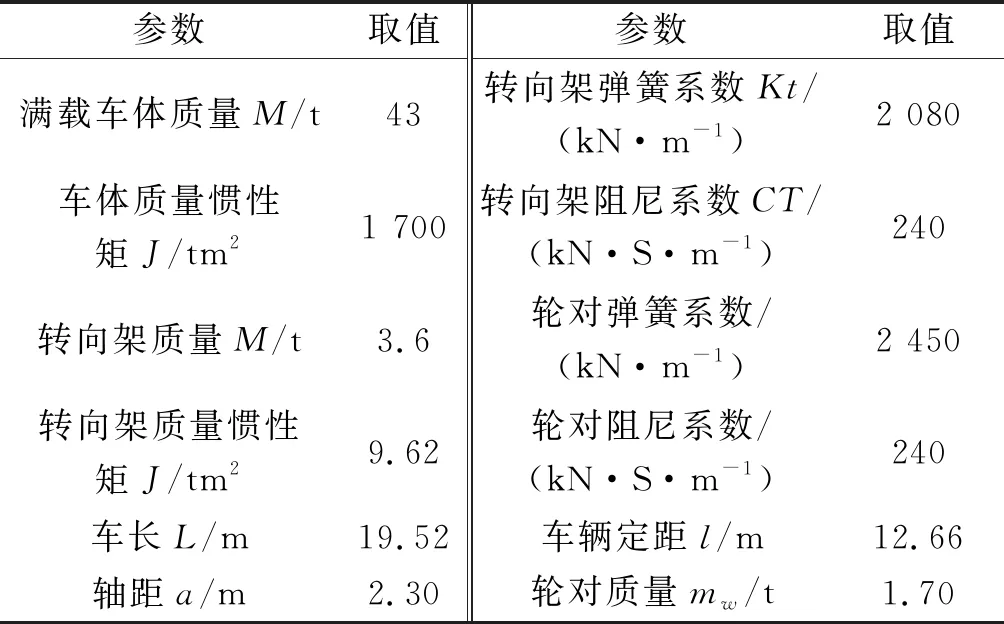
表3 地铁车辆计算参数Table 3 The calculation parameters of metro
根据图10建立车体竖向运动平衡方程为
(5)
式中:m1,m2,m3分别为车体、转向架和轮轴质量;k1,k2,c1,c2分别为一、二系悬挂刚度和阻尼;z1,z2,z3分别为车体、转向架和轮轴位移。
通过变量代换,令ξ1=z1-z0;ξ2=z2-z1;ξ3=z3-z2,方程式(5)改写为
(6)
式中z0为钢轨实测位移。
在列车运行过程中,若忽略轮轨之间的弹跳作用,可以认为车轮的竖向加速的和实测钢轨加速度相等,即
(7)
其中
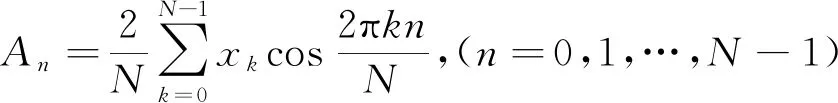
相应地,将ξ1=z1-z0=0代入式(7),可得
(8)
引入达朗贝尔原理,可得到
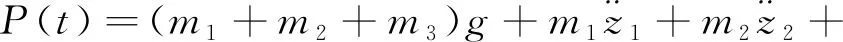
(9)
上述所得的轮轨力为三维空间的轮轨力,通过实测钢轨加速度,并通过求解车体和钢轨体系的动力平衡方程获取轮轨力,由于在实测钢轨加速度时已默认计入了钢轨不平顺的贡献,因此确定的轮轨力考虑了钢轨不平顺的作用。在所建立的二维模型中,需要加入二维线荷载。参考文献[13]将三维荷载转化为二维线荷载,计算式为
F(t)=K·n·M·P(t)/L
(10)
式中:K为修正系数;n为每节车厢转向架数;M为列车车厢数;L为列车长度。参考文献[13]中参数的取值:K=1;n=2;M=6;L=19.52×6=117.12 m。需要说明的是:式(10)所得到的线荷载是三维荷载在二维空间的表现,通过在模型中使用该二维线荷载就可以达到用二维模型来替代三维模型的目的。
实测数据为杭州某车站地铁列车运行过程中钢轨竖向振动速度响应,竖向振动速度时程曲线如图11所示。
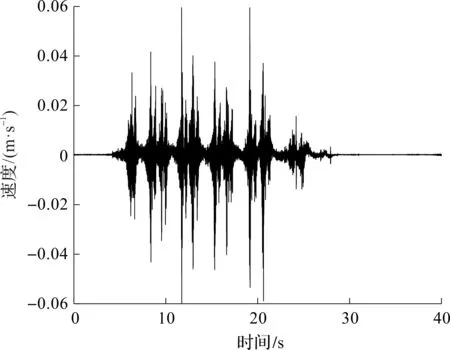
图11 实测竖向振动速度Fig.11 Vertical vibration velocity
将图11所示速度时程曲线转换为加速度时程曲线,结果如图12所示。
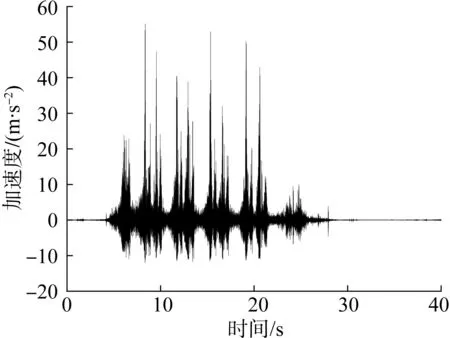
图12 竖向振动加速度Fig.12 Vertical vibration acceleration
根据式(7~10),最终将钢轨加速度转换为轮轨力,结果如图13所示。
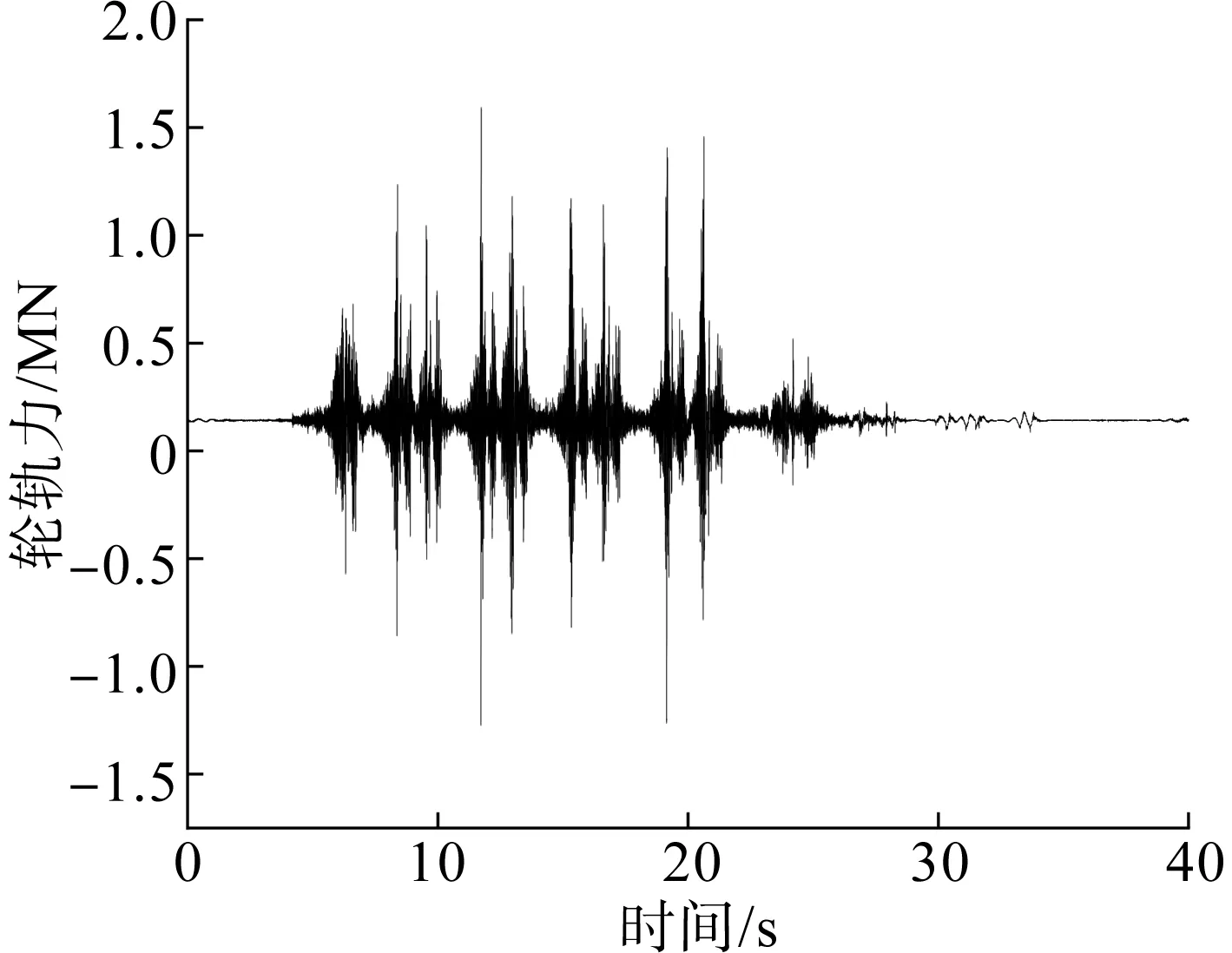
图13 轮轨力Fig.13 Wheel force
4.2 隔振沟在实测轮轨力下的隔振效果
4.2.1 隔振效果时域分析
由于填充沟在实际工程中更为实用,在模型中加入所获取的轮轨力,分析不设置隔振沟(case1)和隔振措施为距离振源10 m,深度12 m的泡沫填充沟(case2)两种工况。
选择两个观测点:隧道正上方地表处点1、地表距离振源24 m处点2。两种工况下的观察点振动加速度时程曲线图和加速度峰值空间分布情况分别如图14,15所示。由图14~15可知:设置隔振沟会在沟前产生堆积效应,使地表振动加速度水平显著高于无沟工况;隔振沟后的地表的振动响应产生明显衰减。
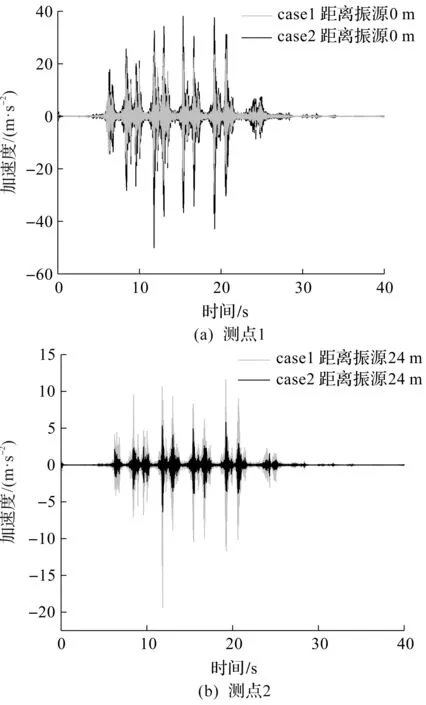
图14 振动加速度时程曲线图像Fig.14 Time history curve of vibration acceleration
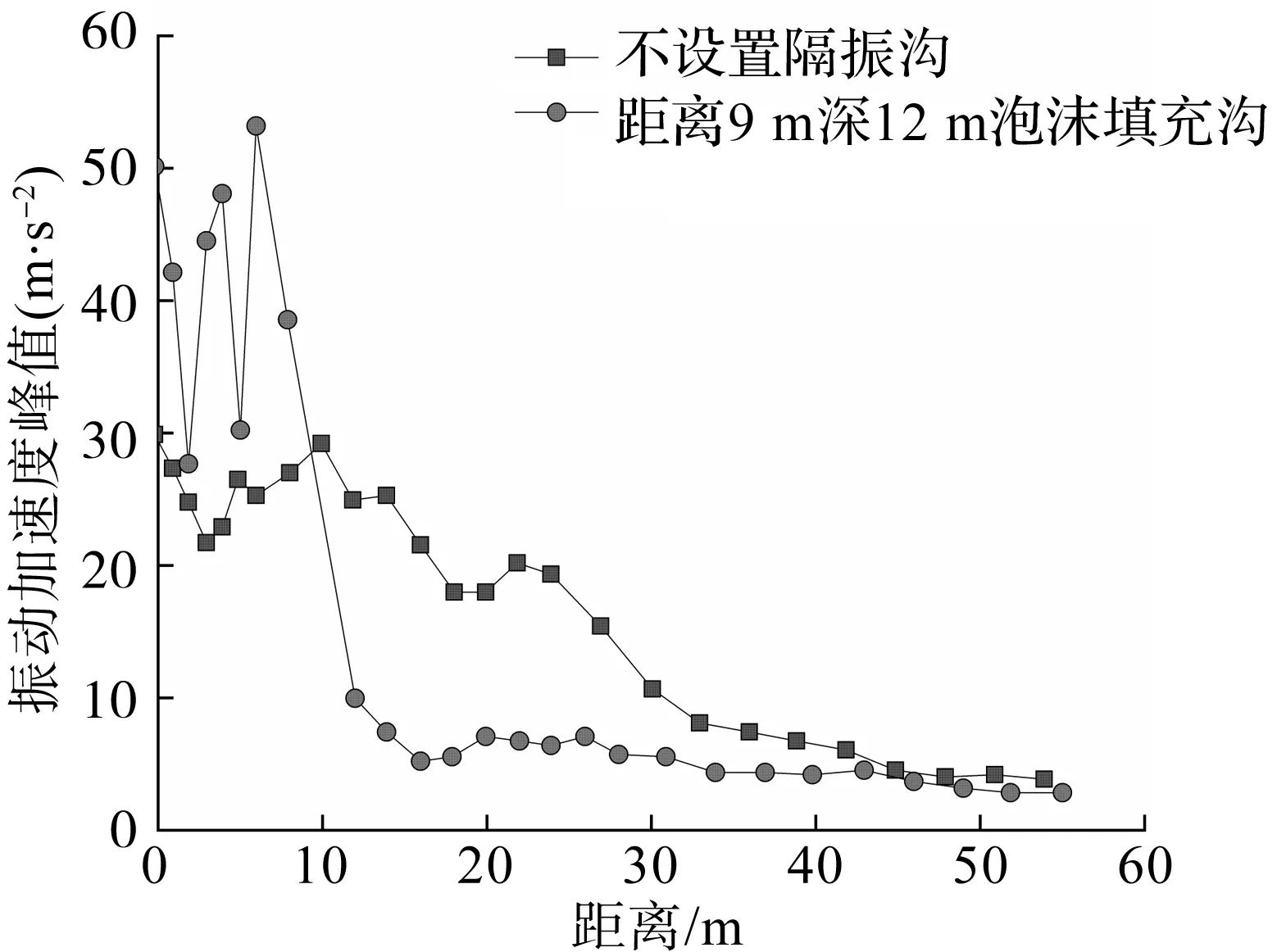
图15 地表振动加速度空间分布图Fig.15 Spatial distribution of surface vibration acceleration
4.2.2 隔振效果频域分析
施加含有各个频率成分的实测振动荷载,会使地表处也产生不规律的振动加速度响应。为分析减振措施对各个频率成分的减振效果,需要对时域数据进行傅里叶变换分析,即通过傅里叶变换把时域上的数据转换为频域的数据,从而研究振动加速度响应的频谱结构与变化规律。
在两种工况下,两观察点的振动加速度频谱如图16所示。观察无沟工况的振动频谱图可以发现:该实测荷载引起的地表振动的主频为80 Hz。对比上述无沟工况和泡沫填充沟工况的振动频域响应图,得到如下规律:图16(a)在沟前产生了堆积效应,该结果与图5结论类似;泡沫填充沟的沟前振幅相较于无沟工况增大,且堆积效应主要集中在20~60 Hz的频段。由图16(b)可知:泡沫填充沟不仅能够有效地对振动产生衰减,而且相较于低频振动,填充沟对高频振动的隔振效果更好。因此,在实际工程中,合理地设置填充沟虽然可以有效抑制高频振动,但是其对低频振动的抑制效果不是很好。
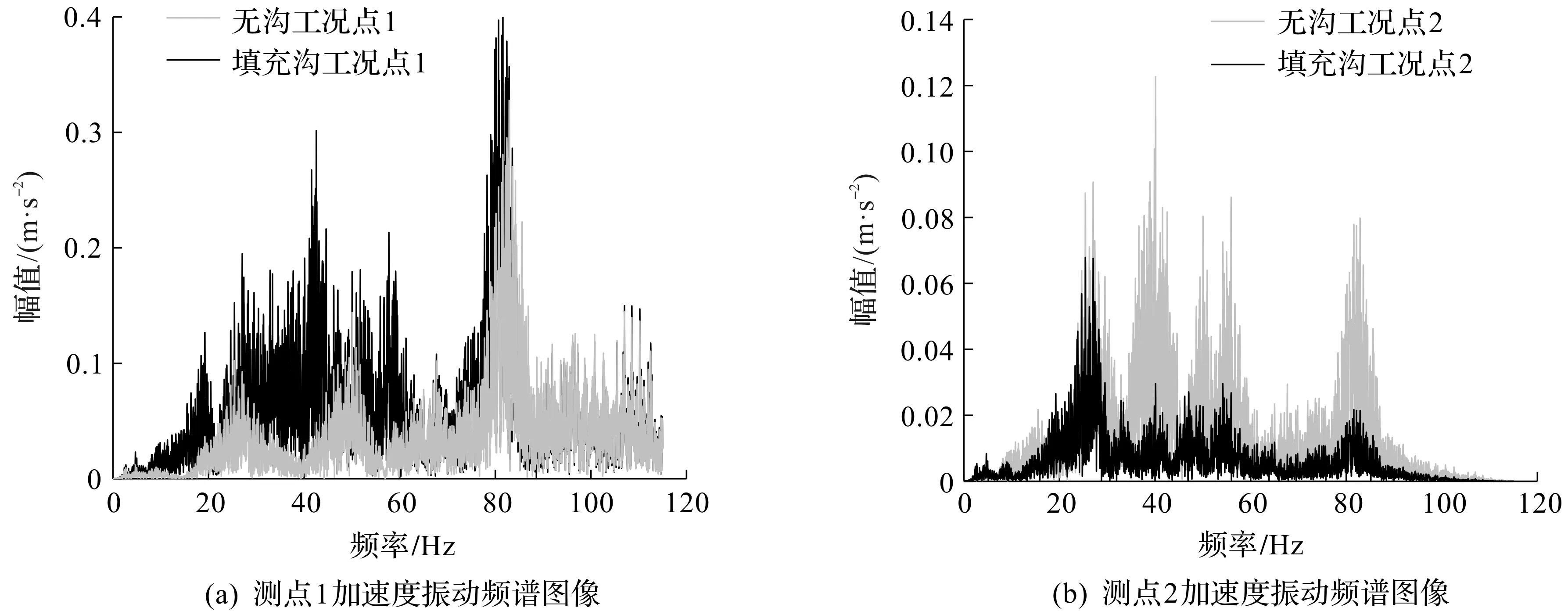
图16 振动频谱图Fig.16 Vibration spectrum diagram
5 结 论
通过有限元软件ABAQUS,建立了二维隧道-土有限元-无限元模型,研究了不同频率地下振源对地面环境振动的影响,同时在模型中加入空沟、填充沟等隔振措施,对不同的隔振措施以及各个隔振措施参数进行分析,分别考虑设置不同位置、宽度的空沟隔振效果和不同材料填充沟的隔振效果,得到如下结论:1) 空沟的深度对隔振效果的影响很大,空沟越深,其隔振效果越好;2) 空沟对高频荷载的隔振效果更好,增加沟深对其隔振效果影响不大,对于低频荷载,需要增加空沟深度才能达到比较好的隔振效果;3) 对于不同位置的空沟,空沟距离振源越近,振动越早衰减;对于低频荷载,其隔振效果随着空沟到振源的距离增加而变好;而随着荷载频率增大,振动在土体衰减变快,空沟距离对隔振效果的影响变得不明显;4) 填充沟隔振材料的材料刚度是影响隔振效果的一个关键因素,隔振材料刚度越小,其隔振性能越好。在实际施工过程中,空沟开挖对土质条件和施工技术都有很高的要求。在开设空沟时,一定要做好调研工作,在保障安全的前提下开挖较深的空沟,若不满足条件,则可以改用填充沟来代替空沟。在设计填充沟时,填充材料应尽量选取刚度较小、松软的材料,以获得较好的隔振效果。
