基于实例和属性加权朴素贝叶斯的电气故障分类研究
2022-06-01舒一飞郭汶昇康洁滢许诗雨
舒一飞,郭汶昇,樊 博,康洁滢,许诗雨,杨 林
(1.国网宁夏电力有限公司营销服务中心,银川 750000; 2.四川大学 电气工程学院,成都 610065)
0 引言
我国电气急速发展,电气化进程显著改善人民生活,但由诸多因素引起的电气故障时有发生,给用电安全、经济建设及电气市场发展带来直接影响。因此及时、快速、准确地对电气故障进行分类,对后续检修、防治,用电线路升级都具有重要意义。居民用电过程中的电气故障主要有漏电,短路,过压,断相等,而电气故障诊断分类的传统方法是基于知识驱动的,该方法由故障诊断知识库、专家知识库、故障诊断推理机等组成,通过将监视的物理征兆导入推理机,并由故障诊断推理机与专家知识库交互,求解出物理征兆下的故障类型,从而完成分类。该方法简单易行,但存在较大的主观性,不能做到对电网监测数据的实时充分利用和准确的故障分析分类。
近年来,诸如神经网络、支持向量机、K近邻、决策树等快速发展的数据驱动方式为故障分类提供了新的手段,由于具备坚实的数学基础,无需先验知识,可仅利用原始的数据特征就完成故障分类任务。但目前这种方法面临挑战,数据驱动方式对数据的数量及质量都有着较高的要求。不充分的数据量将导致网络架构无法拟合,过差的数据质量将使得网络的推广能力下降,对于居民用电故障分类来说,缺乏大量真实故障数据,需通过仿真机产生大量的模拟故障数据片段,不具有较强的推广能力。同时这种方法无法明确地表征数据特征,仅在架构内部进行学习,没有充分完整地对数据属性及特征进行分析和利用,造成了数据资源的浪费。
而朴素贝叶斯将贝叶斯概率、统计学理论和特征条件独立假设相结合,对样本的数据信息进行了严密的推理计算,形成了稳固的理论体系与方法,可以解决数据分析不确定性和不完整性问题。同时为降低属性条件独立假设所带来的负面影响,改进朴素贝叶斯网络分类算法引起了越来越多学者的广泛关注,并由此产生了许多改进的分类模型和学习算法;其中包括通过增加有向边限制条件独立假设的结构扩展、根据待测实例领域选择的实例选择、选择最合理属性子集的属性选择以及属性加权、实例加权五种改进方式。
其中效果较优的为属性加权朴素贝叶斯和实例加权朴素贝叶斯。属性加权是根据属性对分类预测的影响力来为不同的属性分配不同的权值,然后在加权以后的实例样本集上构建贝叶斯分类器;实例加权则根据实例分布情况对训练实例赋予不同的权重,然后在加权的训练实例集上构建分类器;加权方式可以科学严谨地表征数据特征,并且能够充分对其进行计算与分析,使得输入算法框架内的特征信息浓度更高,较充分地提升算法性能表现。
但目前的研究局限于仅采用一种加权方法,未将属性加权与实例加权有机结合在朴素贝叶斯框架内,文章充分考虑不同属性应具有不同重要性,不同实例应具有不同可靠性,在朴素贝叶斯框架内采用双重加权,解决数据分析不确定性和数据不完整性问题,增加对数据片段特征的捕捉和利用,提高算法的实用性和鲁棒性,完成对电气故障高效准确的分类,并可推广至其他分类情形;并与其他基于数据驱动方式的电力故障分类方法进行对比,验证文中算法的有效性。
1 朴素贝叶斯分类
朴素贝叶斯分类是依据贝叶斯定理计算条件概率从而实现分类预测,而贝叶斯定理的前提条件是各条件属性相互独立且对分类结果影响相同,但这在现实中常常难以满足。
如果D
={A
,A
,…,A
,C
}为训练数据集,其中{A
,A
,…,A
}为m
个属性变量,a
为是属性A
的取值,C
={c
,c
,…,c
}是类别总数为q
的类别变量。一个待分类实例x
=[a
,a
,…,a
]属于c
类的条件概率,根据贝叶斯定理有: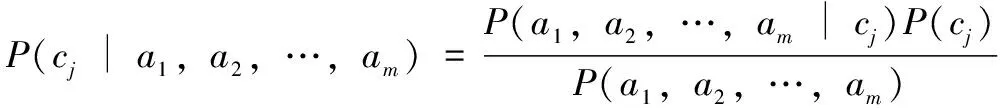
(1)
其中:为进行分类预测的后验概率,P
(a
,a
,…,a
∣c
)为给定第c
类下属性值为[a
,a
,…,a
]的条件概率,P
(c
)是第c
类的先验概率,P
(a
,a
,…,a
)是属性的先验概率,对于各类别都相同。基于各属性相互独立的前提条件,条件概率可表示为:
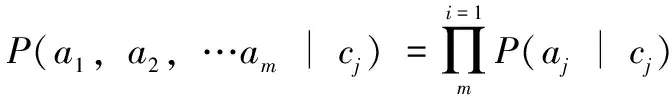
(2)
其中:P
(a
∣c
)表示第c
类下属性a
的条件概率。对于待分类实例x
,基于后验概率最大的原则,朴素贝叶斯分类可表示为:
(3)
式中,P
(c
)和P
(a
∣c
)可以通过训练样本而求得,其计算方式如下:
(4)
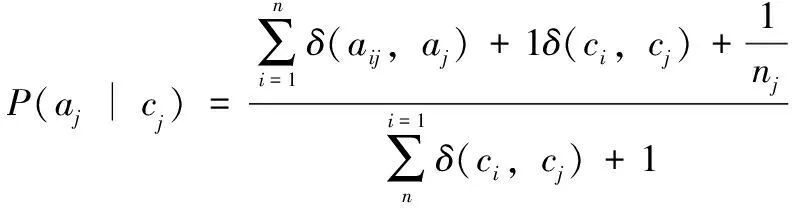
(5)
其中:n
为训练样本总数,a
为第i
个训练样本的第j
个属性值,n
为第j
个属性值在训练样本中的个数,δ
(r
,t
)为二值函数,定义为: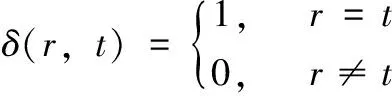
(6)
2 实例和属性加权的朴素贝叶斯
朴素贝叶斯分类基于各条件属性相互独立且对分类结果影响相同的假设条件,这在现实中难以满足。事实上,属性集中的一些属性比其他属性对预测分类更加重要,因此,可以通过属性加权为每个属性分配一个不同的权重,通常,对预测分类越重要的属性为其分配越大的权重,反之亦然。此外,一些训练实例比其他实例对预测分类更可靠,它们对最终模型的影响应该也更大,因此实例加权也是另一种缓解朴素贝叶斯劣势的有效方法。
2.1 双重加权朴素贝叶斯框架
鉴于此,本文融合属性加权和实例加权的优势,提出属性和实例加权的朴素贝叶斯分类(AIWNB)。改进后的AIWNB,一方面采用属性加权方法对不同的属性分别赋予不同的权重,另一方面,采用实例加权方法更准确地估计先验概率和条件概率。因此,AIWNB可以同时继承属性加权的优点和实例加权的优点,从而获得比单一属性加权或单一实例加权更好的性能。
在AIWNB中,将属性权重纳入朴素贝叶斯分类公式中,并将实例权重纳入先验概率和条件概率中。 因此,AIWNB的预测分类可表示为:

(7)
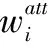
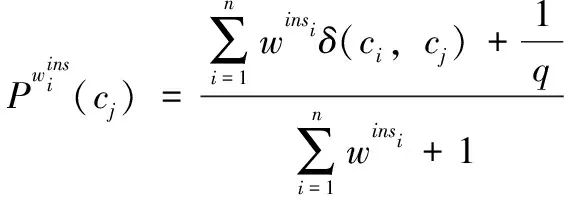
(8)

(9)
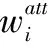

图1 AIWNB算法架构
2.2 实例权值的设置
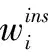
寻找实例权值的方法通常采用积极学习方法和消极学习方法,文中采用了这两种实例加权方法,并通过实验比较两种实例加权算法的差异性;并据此提出二者的较为适宜的使用环境,发挥更大的算法优势。
2.2.1 积极实例加权
为了保持朴素贝叶斯的计算简单性,采用一种简单、高效、有效的方法——基于属性值频度的实例加权滤波器来学习每个实例的权重。这种方法是基于以下观察结果:1)每个属性值的频率包含一些重要的信息,这些信息可以用来定义训练实例的权重;2)每个训练实例的权重与其属性值频率向量和整个训练数据集的属性值个数向量呈正相关。
首先,计算每个属性值的频率,
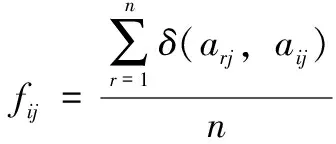
(10)
f
是a
(第i
个实例第j
个属性值)的频率,n
是训练实例的数量,a
是第r
个实例第j
个属性值。令n
为第j
个属性的值的数量,并且可表示为[n
,n
,…,n
];则第i
个实例的权重定义为属性值频率向量与属性值个数向量的内积,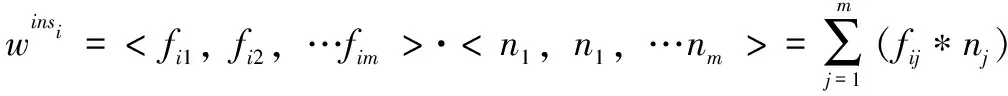
(11)
2.2.2 消极实例加权
不同于积极实例加权,消极实例加权集中注意力于计算并统计训练实例与测试实例间的相关性,虽然时间复杂度较积极加权方式更高,但是可以在分类准确率上得到提升。x
为测试实例,y
为第i
个训练实例,它们间的相似性定义为:
(12)
从式(16)可以看出,s
(x
,y
)简单地对x
和y
的相同属性的数量进行统计的函数,进而粗略地衡量两个实例间的相似程度,定义第i
个训练实例的权重为:
(13)
2.3 属性权值的设置
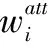
鉴于互信息可以度量每对随机离散变量之间的相关性,因此,文中利用互信息来度量属性-类之间、属性-属性之间的相关性,从而计算得到类关联度和属性间的相互关联度。每个属性的权重可以通过对归一化后的类关联度与平均相互关联度之间的差值进行Sigmoid变换后获取,具体的计算步骤如下所示:
1)属性(A
)-类(C
)的相关性、属性(A
)-属性(A
)的相关性采用互信息来度量,分别定义为: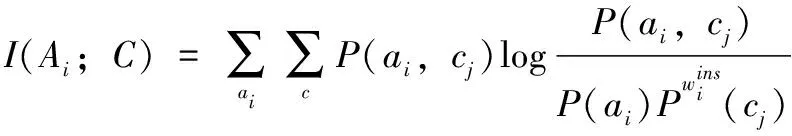
(14)
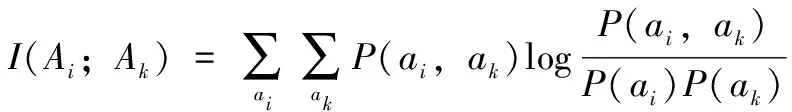
(15)
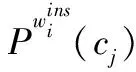
I
(A
;C
)和I
(A
;A
)进行归一化操作:
(16)
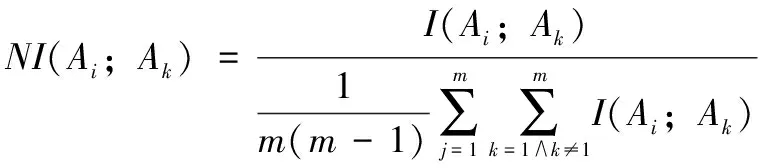
(17)
其中:NI
(A
;C
)和NI
(A
;A
)分别为归一化类关联度和相互关联度;归一化后的各相关性可直接用于运算,不受相关属性的单位限制。3) 将属性权重定义为类关联度与平均相互关联度的差值。

(18)
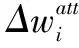
根据上式计算得到的权值可能为负数,应使权值范围落入[0,1],利用sigmoid函数对其进行变换,可得到各属性权值,

(19)
进一步地,将属性加权和两种实例加权相结合,由此得到如下两种用于电气设备故障分类的算法,AIWNB(属性-积极实例加权朴素贝叶斯)和AIWNB(属性-消极实例加权朴素贝叶斯)。
算法1:AIWNB
输入:原始训练集
输出:属性权值向量w
,实例权值向量w
,类别c
1.计算训练集各实例的属性值频率f
及属性值个数n
;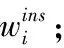
A
的I
(A
;C
)与I
(A
;A
);4.对各属性的I
(A
;C
)与I
(A
;A
)归一化得到NI
(A
;C
),NI
(A
;A
);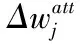

P
(c
),条件概率P
(a
|c
),类别概率c
(x
);8.返回类别。
算法2:AIWNB
输入:原始训练集
输出:属性权值向量w
,实例权值向量w
,类别c
1)计算训练实例y
和待测实例x
的相似性s
(x
,y
);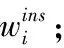
A
的I
(A
;C
)与I
(A
;A
);4)对各属性的I
(A
;C
)与I
(A
;A
)归一化得到NI
(A
;C
),NI
(A
;A
);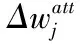
P
(c
),条件概率P
(a
|c
),类别概率c
(x
);7)返回类别。
3 实例验证
3.1 数据预处理
用电数据采集于国网宁夏电气有限公司计量中心,包含高低压用户783户为期31天的三相电压,三相电流,功率及功率因数8项数据。获得数据后对异常数据进行清洗,因电气故障的发生将导致各项数据发生相应变化,仅去除掉空值、数值偏差极大、重复值的数据段。
根据已统计到的用电情况,并结合故障发生时电压电流变化情况,经由相关文献[17-20]及专家标注,可总结为如表1的故障类别及判定依据。如果设备负载是家用热电偶、灯、加热器等,供电线路出现以下4种故障时设备电流、电压和功率变化趋势如表1所示,正常运行数据段标签为“1”。
由于数据集内包含的故障数据段过少,通过在故障数据段内的每个属性叠加随机高斯噪声,增加少量故障数据片段,提升加权朴素贝叶斯对其特征的捕捉能力;随机噪声与真实情况接近,保证数据可用,较大程度模拟真实故障数据。公式如下:

表1 电气故障判据

(20)
其中:μ
为高斯噪声的均值,设置为0;δ
为高斯噪声的标准差,设置为0.1;Gauss
(x
)为生成的噪声,将其与原始数据叠加,完成数据增强。仅对4种电气故障类型进行数据增强,正常运作片段不作处理。原始数据及数据增强后的各电气故障类型数量对比如表2所示。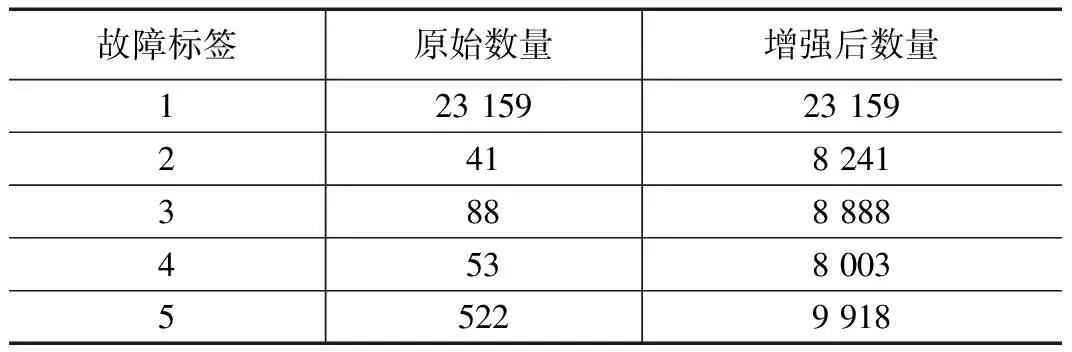
表2 数据增强前后故障类型数量
经由数据增强后总共获得58 209条数据段,随机取得10 000条数据作为测试集,并对训练集与测试集进行归一化,归一化可提高AIWNB的收敛速度以及分类精度,文章采取min-max归一化方法,其公式如下,
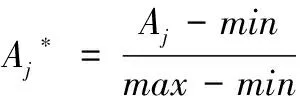
(21)
其中:min
为所有数据段的当前属性A
的最小值,max
为所有数据段的当前属性A
的最大值。3.2 评价指标
为准确评估文章提出模型在分类中的表现,选择准确率(Accuracy
)和F
1分数也作为衡量模型性能和有效性的指标,其计算公式如下: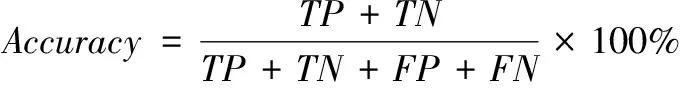
(22)
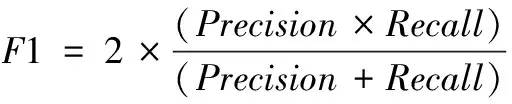
(23)
其中:精准率(Precision
)及召回率(Recall
)计算公式如下,
(24)
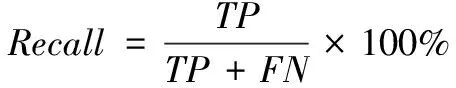
(25)
式中,TP
表示正类别中准确分类样本的数量;TN
表示负类别中准确分类样本的数量;FP
表示正类别中错误分类样本的数量;FN
是负类别中错误分类样本的数量。3.3 结果及分析
按前文所述,对属性及实例分别求解其权值,为使实验更严谨、更具说服性,将分别使用单独属性加权,单独积极实例加权,单独消极实例加权,属性-积极实例加权,属性-消极实例加权与原始朴素贝叶斯实验结果进行对比,获取到效果最佳的加权朴素贝叶斯方式。
3.3.1 属性及实例权值
积极实例加权依赖于对各属性的属性值频率计算,而观察采集到的数据得知实际运行数据的各属性值分散,导致属性值频率f
极小,并不利于计算;因此借用模糊化思想,文中按照表1所述的各属性值变化界定范围,按照类别进行划分,进而计算得到各类实例的权值,如表3所示。
表3 积极实例加权各类实例权值
消极实例加权更注重于训练实例与测试实例的相似性,通过计算每条训练实例与每条测试实例的相似性对实例进行权值的划分,进而改善朴素贝叶斯对不同实例的注意程度,提升分类精度。因数据片段过多,部分实例权值如表4所示。

表4 消极实例加权-部分实例权值
通过对属性-类相关性和属性-属性相关性的残差进行sigmoid变化得到各属性权值,基于互信息的各属性权值如表5所示。

表5 基于互信息的各属性权值
3.3.2 算法性能分析
为全面评价算法的整体性能,文章对各算法的准确率及F1分数进行计算,具体值如表6~7所示,各算法总体准确率如图2所示。
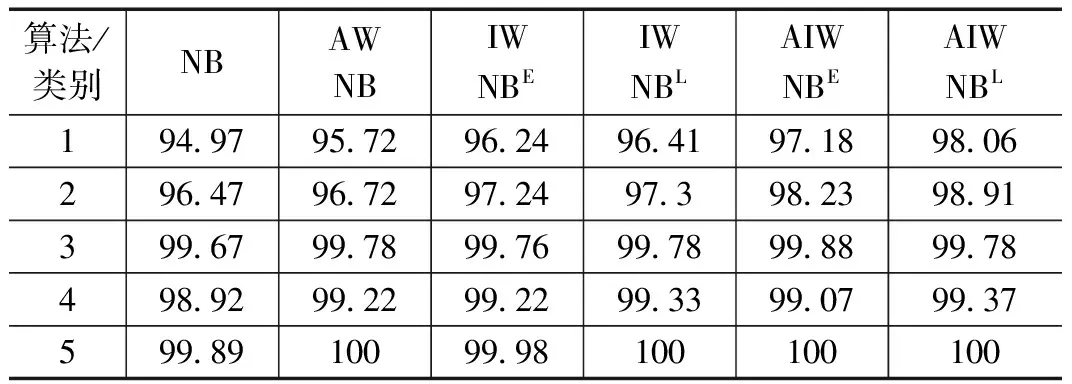
表6 算法准确率对比
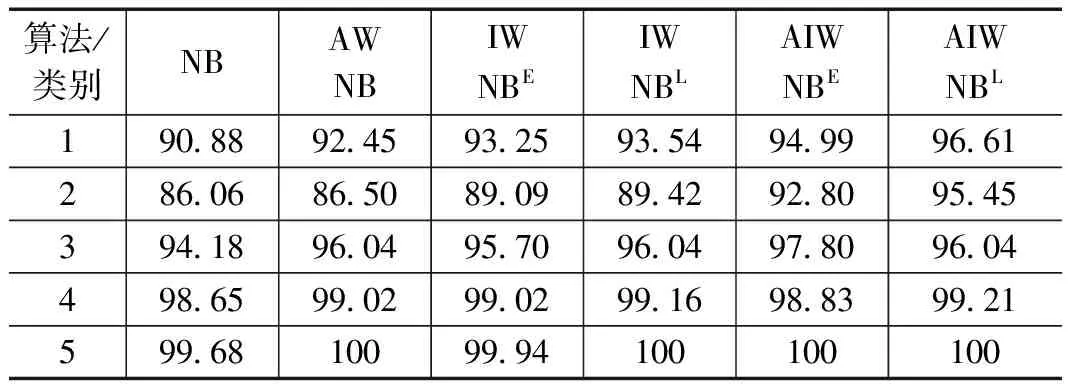
表7 算法F1分数对比

图2 算法总准确率曲线图
可以看出,加权朴素贝叶斯在纳入不同属性、实例的权值后,相较于单一朴素贝叶斯提高了对电气故障分类的准确率,同时获得较高的F1分数,证明在加权朴素贝叶斯能够提取到更多的全局特征,可较大程度提高分类准确率。积极实例加权与消极实例加权的准确率相差较小,但在实验过程中,消极实例加权因需要对训练实例及测试实例逐条计算相关性,耗费更多的运算时间,实际使用中偏向于实时性,可考虑使用积极实例加权。而在电气数据分析和诊断中,消极实例加权的优势更大,可以获得最高的分类准确率。
双重加权朴素贝叶斯较单一朴素贝叶斯的准确率提升为0.11%~3.09%,F1分数提升为0.32%~9.39%。属性-实例双重加权朴素贝叶斯对于待分类的电气故障的高准确率来源于对属性和实例两者权值的同时分析,完整又准确地提取各电气故障的特征分布;并且在第4类与第5类取得接近完全准确的分类效果。属性-积极实例加权朴素贝叶斯(AIWNB)及属性-消极实例加权朴素贝叶斯(AIWNB)的混淆矩阵如图3所示。
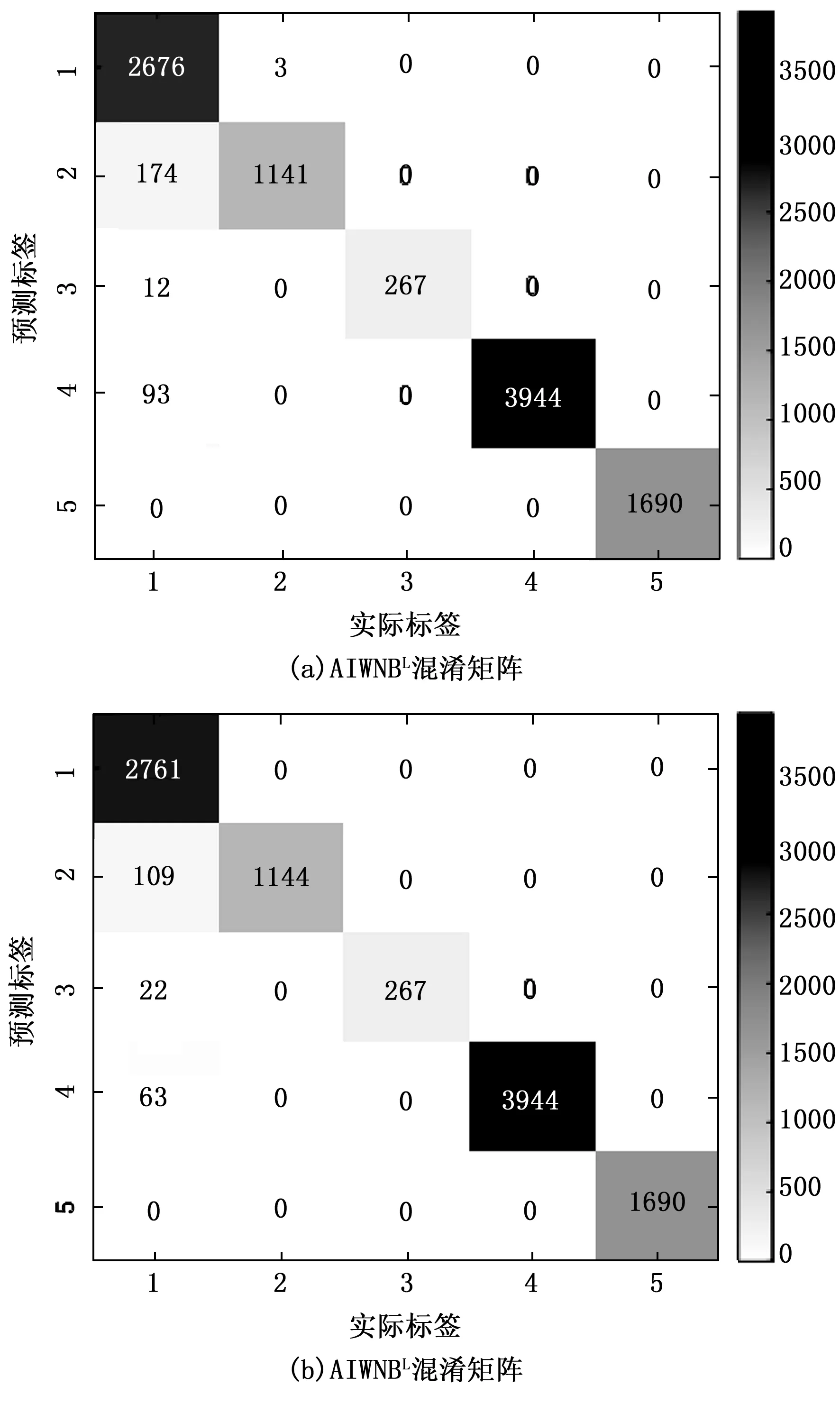
图3 双重加权朴素贝叶斯分类混淆矩阵
AIWNB与AIWNB在面对第2,3,4,5类时几乎可以取得完全准确的分类结果,且在1类的偏差较小;由于消极实例加权更注重于对测试实例的分析,进而会取得更加优良的分类效果,而代价则是增加运算时间,积极实例加权的分类效果稍弱,但运算时间较少,仅需根据属性范围确定权值。
3.4 其他电气故障分类方法性能对比
文中基于属性-消极实例加权朴素贝叶斯的电气故障分类在实际数据中取得了98.06%的准确率,为进一步验证算法有效性,选取K近邻(KNN,k-nearest neighbor),决策树(DT,decision tree)、支持向量机(SVM,support vector machine)、极端梯度提升(XGBoost)等基于数据驱动方式作为电气故障分类方法进行对比;上述机器学习方法使用广泛,分类效果较好,可形成较好的对比组。
为保证对比实验的可信度,在完全相同的训练集与测试集下收集各电气故障分类方法的分类准确率,如表8所示。
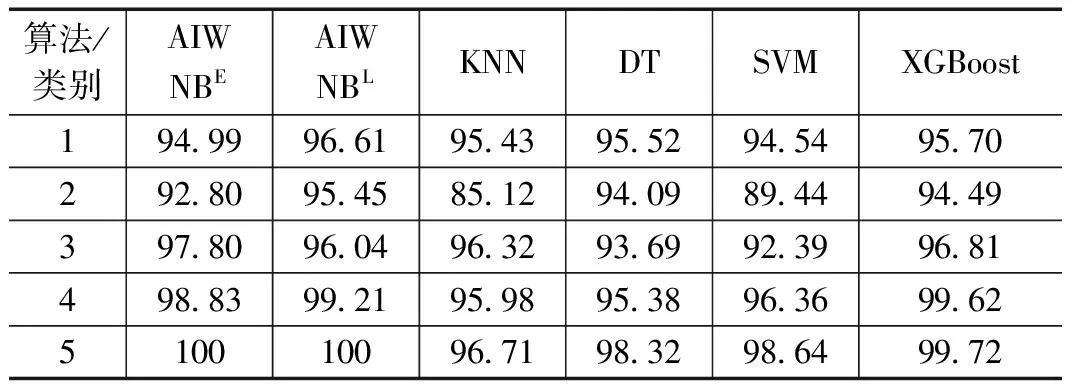
表8 其他电气故障分类方法准确率对比
对各方法指标数据的进一步观察可知,双重加权朴素贝叶斯在获得属性及实例的权值后,能够更加准确地对电气故障进行分类,相较于KNN、DT与SVM取得了更好的分类效果;而XGBoost在第4类取得了更好的分类效果,但XGBoost依赖于梯度的下降,计算量较大,根据实验数据显示运算时间为1.18 s;而AIWNB的运算时间仅为0.536 s,具有更好的实时性。
4 结束语
文章采用朴素贝叶斯架构,提出了基于属性加权和实例加权的电气故障分类算法。该算法通过互信息统计属性-类间依赖性和属性-属性冗余度获取各属性权值,提升算法对各属性特征的提取与利用能力;分别计算实例属性值频率和实例间相关性完成积极、消极实例加权,进一步提升算法对数据全局特征的把控能力。在实验过程中,双重加权朴素贝叶斯在准确率、F1分数优于单独加权朴素贝叶斯、单一朴素贝叶斯与其他常用分类方法,较显著降低误分数量,提高分类实时性。文章算法是通用算法,可以推广至其他待分类情形,譬如心电信号、岩爆等。
