整流罩分离过程中运动位姿测量技术研究

袁 媛，高 越，孙增玉，王 杏，刘 柯

（北京航天计量测试技术研究所，北京 100076）

1 引 言

整流罩作为运载火箭的重要组成部分，可有效保护内部载荷免受外部气动力和气动加热等的影响，进而改善火箭飞行性能。当运载火箭飞行到大气层外后，需要抛离整流罩以减小飞行负荷，否则很有可能导致发射任务失败。整流罩与火箭进行分离时，要保证：①分离前两者的连接整体性；②分离时两者的分离高可靠度；③整流罩分离前后对火箭和内部载荷的正常运行没有影响。为保证整流罩安全与箭体脱离，整流罩需以某过顶角速度或平抛速度与箭体分离且保持足够分离距离，但由于整流罩分离时的相关参数在火箭正常飞行时难以获取，故通过地面试验获取整流罩分离时的运动位置姿态、分离轨迹及分离速度等相关参数具有重要的参考意义。视觉测量是一种非接触光学测量方法，广泛应用于航空航天对接任务、移动机器人视觉导航、工业平台定位等多个领域中。双目视觉技术利用两个图像传感器同时采集测量图像，可以从含有视差的一对对应平面图像中恢复出任意特征点的三维信息，采集过程瞬间完成。本文通过双目视觉对整流罩关键点的运动轨迹进行高速测量，对图像序列中的关键点所具有的特征进行检测与提取，结合深度图像和灰度图像，计算获得图像中关键点的实时三维姿态、速度等信息。

2 双目立体视觉测量模型

双目立体视觉的基本原理是视差测量，利用两台相机在不同方位同时采集包含被测特征的两幅图像，且两台相机空间位姿信息已知，通过图像处理、立体匹配等技术获取被测特征点在二维图像平面上的共轭像点，构建光线三角交会约束，计算图像对应共轭点间的位置偏差，进行深度信息提取，进而解算被测物体表面特征点的空间三维坐标值。双目立体视觉模型如图1所示。

图1 双目立体视觉模型Fig.1 Binocular stereo vision model diagram

设左相机o－xyz为世界坐标系，图像坐标系为O－XY，有效焦距为f；右相机坐标系为oxyz，图像坐标系为O－XY，有效焦距为f，由透视变换模型得到

o－xyz坐标系与o－xyz坐标系间的空间关系可以用转换矩阵M表示为

M表示为：M＝［R T］

由公式（1）～（3）可知，对于o－xyz坐标系中的空间点，两相机像面点之间的对应关系为

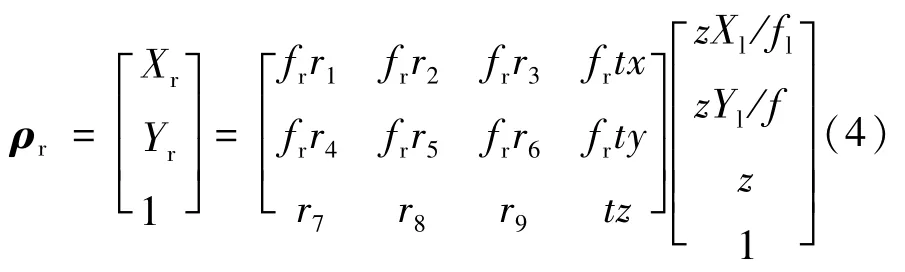
空间三维坐标可以表示为

因此，已知焦距f、f和空间点在左右相机中的图像坐标及旋转矩阵R和平移矩阵T，即可解算空间任一点的坐标。

3 双相机内外参数标定

相机标定是基于成像模型来确定左、右相机的内部参数及左右相机之间的外部参数，以便正确建立空间中某点和它在图像平面上对应像点之间的关系。相机标定需要同时完成内参数和外参数的标定，内参数即相机和镜头的内部畸变参数，包括焦距、主点位置、等效像素、畸变因子等；外参数即两相机坐标系间的空间转换关系，包括位置关系和角度关系。

式中：s——任意非零尺度因子；A——内参矩阵，定义为

式中：（u，v）——主坐标点；α、α——分别为u轴和v轴的尺度因子；r——u轴和v轴不垂直因子，由公式（6）求解可得相机内部参数。

考虑镜头畸变，引入如下畸变模型

此外，如果可能，可以把第三稿的完成时间安排在课内，老师可以给予更加个性化的指导，帮助能力较弱的学生举一反三，修改效果更佳。

将每幅图像解得的A，R，T及每点对应的图像和世界坐标点对，畸变参数k，k的初值为0，通过非线性优化得到全局最优解。

4 对极几何约束关系

建立同一空间点在左、右相机中所成像点的唯一对应关系，可以依靠对极几何约束。对极几何约束就是左图像的特征靶标在右图像上的匹配点必处于该点的极线方向上。对极几何约束关系的原理示意图，如图2所示。

图2 对极几何约束关系原理示意图Fig.2 Schematic diagram of epipolar geometric constraint relations

测量点S在左右相机中的成像点分别为m和m′，其中，m和m′互为匹配成像点；极点是两相机光学中心O和O的连线与相面的交点，分别记为e和e′；极线是由极点和像点确定的直线，记为lm和l′m′。对极几何约束关系可表示为

式中：m＝（x，y，1）；m′＝（x′1，y′1，1）；F——基本矩阵。基本矩阵F是将左相机图像I中像点m映射成右相机图像I′中对极线l′m′的矩阵，其定义

式中：K和K′——分别为左右相机图像的内参矩阵；［t］——反对称矩阵。T＝（tx，ty，tz），为左右相机坐标系之间的平移矩阵；R——左右相机坐标系间的旋转矩阵。其中，

利用对极几何约束关系寻找匹配点时，若已知左右像点的齐次坐标m和m′及基本矩阵F，由式（10）就可判断两像点是否匹配。设F为

若已知两相机匹配点对的图像齐次坐标，将其代入式（10），得到含有8个未知数的线性方程。若求解此方程，则需要至少8个已知匹配点对，建立线性方程组，便可以实现基本矩阵F的求解。但本身像点齐次坐标存在误差，故需要采用非线性优化方法进行优化。

以上述线性方程组求得的F作为非线性优化方法的初值，利用左右像点到对应像面极线的距离平方和的最小值作为约束条件，可得F的优化估计值，优化方程为

式中：d（m，Fm′）、d（m′，Fm）——分别为像点m、m′到对应极线的距离，Fm′、Fm——分别为两极线的解析表达式。

基于非线性优化方法得到基本矩阵F的最优估计值，针对某一像点m，遍历所有像点m′（j＝1，2，…n），按照式（15）计算C（j＝1，2，…n），设定阈值C＝1×10，对于小于C的C，认为其对应的点m′为像点m的匹配点，则

5 运动位姿测量方案

位姿测量系统基于双目立体视觉原理搭建，两台高速相机以一定的交会角度对测量区域进行高速同步拍摄，经位姿解算可得立体空间不同特征点的三维空间坐标。测量前，在测量物体上布置若干个立体球形回光反射光学靶标，如图3所示，其采用特殊的高反射材料，可保证相机在不同位置获取靶标图像特征的一致性，进而提高位姿解算的精度。位姿测量系统布局示意图如图4所示，位姿测量系统由两台高速测量相机、数据处理计算机、光源及同步控制器等设备构成。

图3 球形光学靶标Fig.3 Spherical optical target

图4 位姿测量系统布局示意图Fig.4 Schematic diagram of the layout of the pose measurement system

试验过程中，整流罩按照预定方式分离，整个分离轨迹在相机视场内，通过追踪整流罩表面具有高反光特性的特征靶标，经过滤波、高光处理、阈值分割、形态学运算等一系列图像处理工作，完成对整流罩上关键点的运动轨迹的测量。测量过程中由同步控制器控制两台高速相机，同步完成高速图像采集工作，由位姿解算软件完成后续的图像处理及三维解算等工作。

在对整流罩分离过程中的各特征点运动姿态进行测量过程中，通过不同关键点的三维空间坐标，进而分析可得整流罩表面各特征点的速度、加速度等关键信息，通过对关键信息的判断可指导整流罩结构设计等的合理性。然而在整流罩分离过程中，图像中的各特征点间的相对位置关系实时变化，为避免各特征点间解算时匹配出现错误，本文基于halcon软件编写完成对各特征点的图像处理、识别及跟踪测量算法，结合极线约束匹配，很大程度上消除了图像之间特征点的误匹配问题。该算法可自动跟踪特征点，进而解算得到空间物体的三维六自由度姿态信息，提高了姿态解算效率。特征点跟踪测量流程如图5所示，通过相机内外参数标定，在获得两相机内部参数及外部参数的前提下，读取初始时刻物体测量图像，处理得到初始时刻某特征点P的图像像素坐标值。设置特征点P的矩形区域窗口，并返回此矩形区域的补码图像，对图像进行阈值分割、特征提取，并判断特征点的个数是否为1。基于极线约束完成左右图像像点对的精确立体匹配，循环遍历所有时刻的图像，获得此时刻特征点的图像像素坐标，并实时更新矩形区域的窗口位置，完成所有时刻下整流罩表面所有特征点的三维坐标解算，以备后续分析处理数据。

图5 特征识别跟踪流程图Fig.5 Feature recognition and tracking flowchart

6 试验与分析

当整流罩半罩分离时，控制系统发出指令，两个半罩在推力下向外运动，双目高速摄影测量系统以500 fp／s的速度完成分离过程中图像的采集，通过图像处理及跟踪识别完成一个半罩上的多个特征点在分离过程中的空间运动轨迹，进而分析出各特征点的角速度曲线及各点平均速度曲线。图6为整流罩半罩某特征点经滤波后沿X方向的速度随时间变化的情况，图7是整流罩半罩上多特征点的三维坐标在整流罩分离过程中每一时刻的三维坐标实时变化曲线。

图6 某一特征点沿X向速度随时间变化的曲线Fig.6 A characteristic point along the X-direction speed versus time curve

图7 多特征点实时三维坐标测量值变化曲线Fig.7 Multi-feature point real-time three-dimensional coordinate measurement value change curve

7 结束语

基于双目视觉原理开展了整流罩分离过程中多特征点的动态跟踪测量技术研究，基于特征点的图像处理、识别及跟踪测量算法，结合极线约束匹配，很大程度上消除了图像之间特征点的误匹配问题，实现精确立体匹配，进而解算得到每一个特征点在整流罩分离过程中的三维坐标、各特征点的实时速度，可有效评估整流罩分离过程的安全性和可靠性。