构造临界图形，直观分析参数取值范围

陈贇

有些新定义问题综合了平移变换的内容。随着平移的位置不同，往往会有多处临界情形，我们如果能准确构造出临界图形，就能直观分析参数的取值范围。下面结合一道新定义问题，解读新定义，构造临界图形，让“思维可视化”。

例题 在平面直角坐标系xOy中，对于已知点P和图形W，若对图形W上任意两点M和N，都有PM≤3PN成立，则称图形W为点P的“关联图形”。

已知⊙T的圆心为T（t，0），半径为2，直线y=x-1与x轴、y軸分别交于G、H两点，若在线段GH上存在点P，使得⊙T是点P的“关联图形”，分析t的取值范围。

【思路解析】解题之前，先要厘清新定义中PM、PN需要满足的条件，除了PM≤3PN以外，还需要理解当PM取最大值，PN取最小值时，PM、PN满足PM≤3PN，这样才符合新定义所说的“关联图形”。

【思路突破】先思考对于半径为2的⊙T，平面内一点P到圆上的点的最大距离和最小距离有怎样的特点？应该作直线PT，与圆相交于两点，进而分析出它们是否符合新定义的不等式要求。由点和圆的三种位置关系来分类讨论，厘清点P的可能位置，是“破题”关键。下面，我们构造示意图分析。

如图1，当点P在⊙T外时，设PN=x，需要满足x+4≤3x，解得x≥2，即点P在以点T为圆心，半径为4的大圆上及其外部。

如图2，当点P在⊙T上时，PN=0，不满足不等式，这种情形舍去。

如图3，当点P在⊙T内时，设PN=x，需要满足4-x≤3x，解得x≥1，即点P在以点T为圆心，半径为1的小圆上及其内部。

接下来，构造图4进一步分析。

当线段GH上存在点P在最大圆T（半径为4）上及外部时，符合新定义“关联图形”;当线段GH上存在点P在最小圆T（半径为1）上及内部时，符合新定义“关联图形”。

接下来构造图5、图6、图7、图8，进一步分析可能的临界情形。

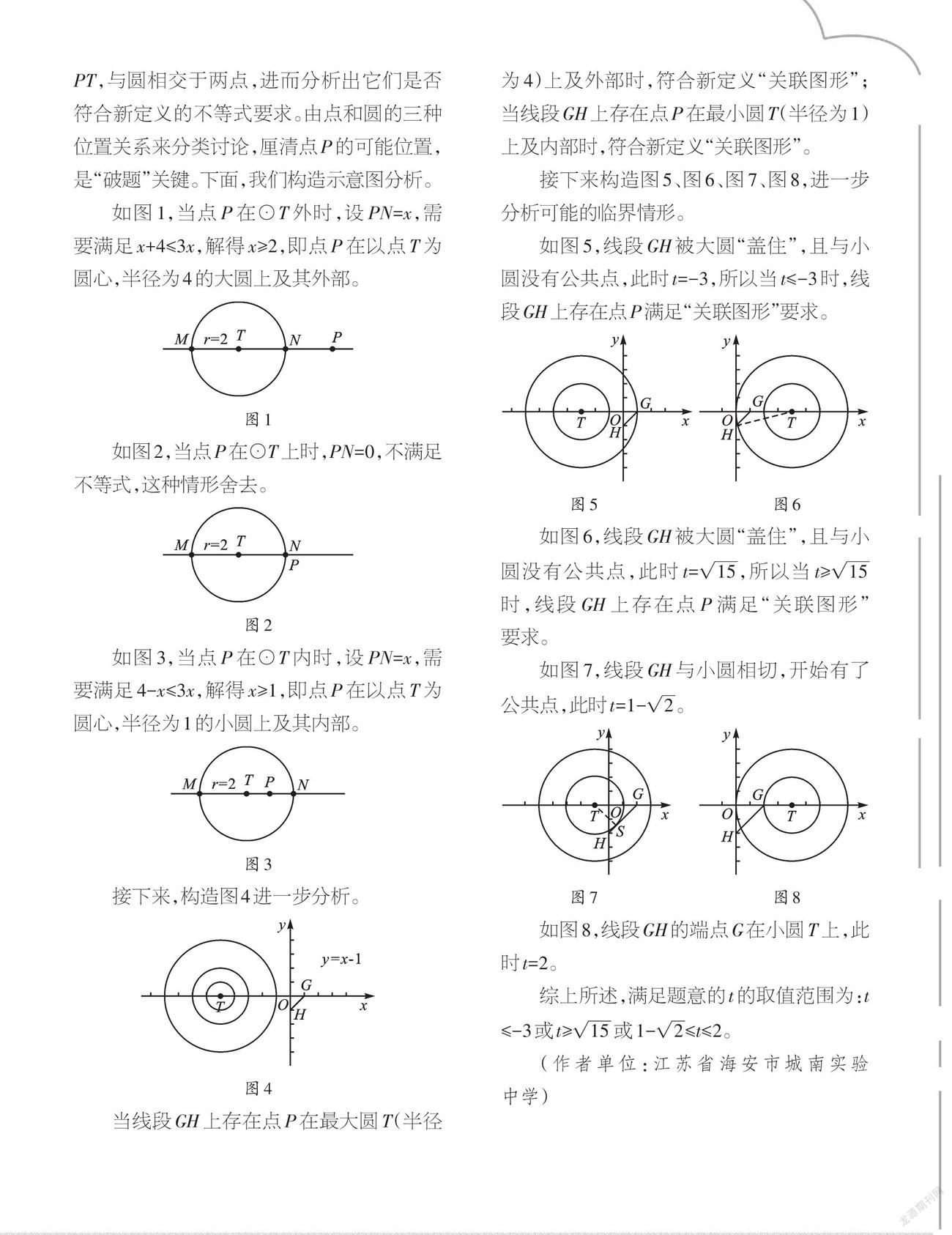
如图5，线段GH被大圆“盖住”，且与小圆没有公共点，此时t=-3，所以当t≤-3时，线段GH上存在点P满足“关联图形”要求。

如图6，线段GH被大圆“盖住”，且与小圆没有公共点，此时t=[15]，所以当t≥[15]时，线段GH上存在点P满足“关联图形”要求。

如图7，线段GH与小圆相切，开始有了公共点，此时t=1-[2]。

如图8，线段GH的端点G在小圆T上，此时t=2。

综上所述，满足题意的t的取值范围为：t≤-3或t≥[15]或1-[2]≤t≤2。

（作者单位：江苏省海安市城南实验中学）