基于子空间结构正则化的L21非负矩阵分解高光谱解混

陈善学 刘荣华

(重庆邮电大学通信与信息工程学院 重庆 400065)

(移动通信技术重庆市重点实验室 重庆 400065)

1 引言

高光谱图像凭借丰富的光谱信息，在目标识别、图像分类和矿物勘探等领域都有广泛的应用。然而，由于地面的复杂情况和空间分辨率的限制，单个像元可能由多种地物组成，导致混合像元现象，这种现象普遍存在于高光谱图像中，严重阻碍了高光谱图像的应用[1]。因此，为了提高高光谱图像的应用性能，通常利用高光谱解混来分解混合像元[2]。高光谱解混的目的是将混合像元分解成一组纯光谱的集合，称为端元，以及每种端元在该像元中的相应比例，称为丰度[3]。

高光谱解混主要依赖于两种混合模型：线性混合模型(Linear Mixing Model, LMM)和非线性混合模型[4](Nonlinear Mixing Model, NMM)。非线性混合模型难以物理建模和恢复，而线性混合模型因其简单而有效的混合过程备受关注。基于LMM，像元分解技术通常可以分为基于几何、稀疏回归和统计3种方法[5]。

几何算法假设高光谱数据存在于凸单形体中，端元精确地位于单形体的顶点。最小体积单形体分析算法[6]、最小体积外包单形体算法[7]和迭代约束端元[8]是比较流行的几何方法。稀疏回归方法假设像元可以用光谱库中已知纯光谱的线性组合的形式来表示。在统计框架下，高光谱分解可以表示为盲源分离问题[9]。代表性的算法包括独立成分分析[10]和非负矩阵分解(Nonnegative Matrix Factorization, NMF)[11]。NMF是盲源分离技术最常用并广泛应用于高光谱图像解混的方法。然而，由于NMF目标函数的非凸性，算法通常陷入局部极小值。为了缩小解空间，徐光宪等人[12]将最小体积单纯形约束融入到NMF模型中，展现了高光谱图像中光谱特性与丰度特性之间的关系。Wang等人[13]提出了端元相异度约束NMF方法，该方法假定端元信号本身是平滑的。

另一种缩小解空间的策略是对丰度添加约束。Qian等人[14]探索了使用L1/2正则项来限制丰度的稀疏性，不仅提供更稀疏的解，而且计算效率高。Candès等人[15]提出重加权稀疏约束，证明了通过加权L1范数并迭代更新权值，可以增强丰度的稀疏性并提高L1最小化框架的恢复性能。文献[16]提出了多先验集成约束的NMF方法，引入全变差正则项来捕捉丰度的分段平滑结构。由于流形方法的空间结构学习能力，文献[17]将流形结构引入到NMF模型中来分离相似的相邻像元。在文献[18]中，Lu等人提出一种基于子空间聚类约束的稀疏NMF方法，利用聚类来寻找空间结构信息。最近，Zhou等人[19]提出利用子空间结构来捕获全局空间分布信息。

虽然这些方法取得一定的效果，但由于传统的NMF应用于高光谱解混时，对噪声和异常值的处理不够鲁棒，其解混效果会受到影响。Huang等人[20]提出了一种融合L21范数和L12范数的NMF模型，同时实现了频带噪声和像元噪声的鲁棒性。周昌等人[21]尝试使用L21NMF模型，将其应用于图像聚类的研究，取得了较好的解混效果。

本文提出一种新的基于子空间结构正则化的L21非负矩阵分解算法(L21Nonnegative Matrix Factorization based on Subspace Structure Regularization, L21NMF-SSR)，充分利用了丰度的稀疏性和空间结构信息。首先，利用L21范数代替标准NMF中的F范数，对模型进行了改进。其次，混合像元仅由几个端元组成，且每个像元都可以表示为这些端元的线性组合。同时，谱库的端元数量远远多于混合像元中包含的端元数量，丰度本身就是稀疏的。因此，引入了双重加权稀疏正则项来增强L21NMF模型中丰度矩阵的稀疏性。最后，在此基础上集成子空间结构正则项，并利用低秩表示(Low-Rank Representation, LRR)方法[22]来学习表示所有地物的子空间结构。

2 预备知识

2.1 线性混合模型

2.2 非负矩阵分解

3 基于子空间结构正则化的L21非负矩阵分解模型

3.1 L21NMF-SSR模型

在本文提出的算法中，用L21范数代替标准NMF模型的F范数，即

为了充分利用丰富的先验信息，提高解混性能，本文在L21NMF模型基础上，对丰度矩阵增加了两种约束。在真实高光谱图像中，混合像元仅由几个端元组成，且每个像元都可以表示为这些端元的线性组合，同时谱库的端元数量远远多于混合像元中包含的端元数量，丰度本身就是稀疏的。因此，本文引入双重加权稀疏正则项来提高L21NMF模型的估计性能和稀疏性，可以得到比L1正则项更好的稀疏结果。双重加权L1最小化问题可以定义为

3.2 模型优化

3.3 算法的实现

表1 L21NMF-SSR算法(算法1)

4 实验结果与分析

本文在模拟数据集和真实数据集上进行了实验，以评估L21NMF-SSR算法的有效性，并与L1/2-NMF[14], RSNMF[24], SRRNMF[11], SSRNMF[20]和SSR-NMF[19]等算法进行了比较。对比算法中的参数，均使用原文献中的选择。对于所有的实验，本文使用光谱角距离(Spectral Angle Distance, SAD)和均方根误差(Root Mean Square Error, RMSE)两种常用的方法评价算法的性能。SAD用来计算端元估计值eˆ 与端元真实值e之间的夹角距离，定义为

从式(30)、式(31)中可以看出，SAD和RMSE的值越小，则估计值与真实值差异越小，说明提取的结果越好。

为了保证算法的有效性，所有实验在相同条件下重复20次，取平均值作为最终实验结果。

4.1 模拟数据实验

使用MATLAB高光谱合成工具箱[25]生成与真实场景图像相似的模拟数据集。在模拟过程中可以选择如图像大小、丰度分布和端元数量等不同的参数来生成模拟数据集。实验中所需的端元光谱均来自USGS数字光谱库，而相应的丰度是根据球面高斯场生成的。图1显示了5种地物的光谱。其中，构建的模拟数据集像元大小为100×100，光谱波段为224。

图1 模拟数据中的光谱曲线

图2 L21NMF-SSR在λ1值下的SAD和RMSE

此外，真实高光谱图像中普遍存在噪声，为了模拟数据采集过程，在模拟图像中添加不同的噪声等级，信噪比的定义为

4.1.2 不同端元数目的鲁棒性

本实验用来探讨不同的端元数目对6种方法解混性能的影响。在本实验中，将SNR设置为25 dB，端元数目P从5变化到10。在此过程中，所有算法均使用相同的模拟数据。结果如图4所示。综合比较结果，L21NMF-SSR的性能最好，而L1/2-NMF的性能最差。由此可以证实L21NMF-SSR具有很强的优越性和鲁棒性。

图3 L21NMF-SSR在λ2和α值下的SAD和RMSE

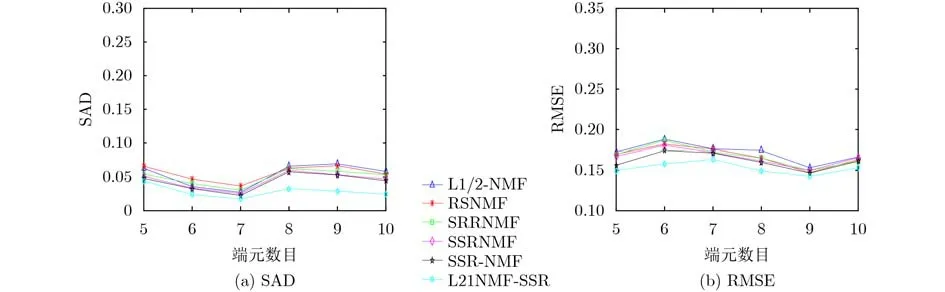
图4 不同算法在不同端元数目的性能比较

4.1.3 性能分析

高光谱图像的获取过程中很容易受到噪声的干扰，对于解混这是一个挑战。本实验中，设置了信噪比等级分别为15, 20, 25, 30和35 dB的高斯噪声。表2和表3显示了各种算法在不同信噪比级别下的SAD和RMSE结果值。其中，最佳结果使用粗体标注。从表2和表3可以看出，在各种噪声等级下，L21NMF-SSR算法获得了最低的SAD和RMSE值，说明该算法提取的端元和丰度精度更优。与大多只使用稀疏约束或只改进模型的方法相比，集成空间结构信息的SSR-NMF具有更好的性能，这表明了子空间结构捕获空间信息的有效性。然而，相比SSR-NMF算法，L21NMF-SSR对标准NMF模型进行了改进，同时将双重加权稀疏加到L21NMF结构中，使得L21NMF-SSR的性能更优。随着SNR的减小，噪声对各个算法性能的影响越来越大，我们的算法具有明显的优势以及较强的鲁棒性。

表2 不同算法在不同信噪比级别下的SAD值的比较

表3 不同算法在不同信噪比级别下的RMSE值的比较

4.2 真实数据实验

(1)Jasper Ridge是一种广泛应用于高光谱解混实验的高光谱数据，在380～2500 nm范围内由224个波段组成。为了避免大气影响和水蒸气问题，我们去掉了1～3, 108～112, 154～166和220～224波段，保留了198个波段，因此本实验只使用100×100像元的图像。数据集包含的4种端元是水体、土壤、道路和树木。

表4显示了不同算法在Jasper Ridge数据集下的SAD值，最后一行是在不同算法下所有地物的SAD平均值。其中，最佳结果使用粗体标注。从表4可以看出，对于水体和道路这两种端元以及均值，L21NMF-SSR得到更低的SAD值，表明了L21NMFSSR提取的端元整体更接近真实的端元。表5显示了不同算法下的RMSE值，其中L21NMF-SSR获得最小的RMSE值，表明了重构图像与真实图像的差异最小。因此，与其他方法相比，在Jasper Ridge数据集下L21NMF-SSR算法有更好的性能。

表4 不同算法在Jasper Ridge数据集的SAD值对比

表5 不同算法在Jasper Ridge数据集的RMSE值对比

图5显示了L21NMF-SSR提取的端元特征与参考特征的对比，从中可以看出提取的端元与真实端元的一致性。不同算法得到的丰度图如图6所示。可以观察出，L1/2-NMF和RSNMF容易受到噪声的影响，特别是水体和道路。整体来看，L21NMF-SSR受噪声的影响较小，对噪声有良好的鲁棒性，取得较好的丰度结果。

图5 L21NMF-SSR提取的端元特征与参考特征的对比

图6 不同算法的丰度图对比

(2)Urban数据集是另一个应用广泛的高光谱图像数据集。它包含了307×307个像元，每个像元有210个光谱波段，将1～4, 76, 87, 101～111, 136～153和198～210的波段移除，得到162个波段的图像。数据集主要包含4种地物：沥青、玻璃、树木和屋顶。

表6显示了在不同算法下不同地物的SAD值。同样地，最佳结果使用粗体标注。通过数值之间的比较可以看出对于沥青、玻璃、屋顶以及均值，L21NMF-SSR取得更低的SAD值。表7是不同方法在Urban数据集下的RMSE值，比较前5种算法，可以看出使用子空间结构的SSR-NMF算法比其他算法取得更低的RMSE值，但是L21NMF-SSR减少了噪声与异常值的影响，同时获得更加稀疏的结果，因此，获得了更好的解混效果。

表6 不同算法在Urban数据集的SAD值对比

表7 不同算法在Urban数据集的RMSE值对比

图7显示了L21NMF-SSR提取端元与真实端元的一致性。不同方法得到的丰度图如图8所示。可以观察出，L21NMF-SSR取得更好的丰度结果。综上可得，在Urban数据集下，L21NMF-SSR算法具有较好的解混性能。

图7 L21NMF-SSR提取端元特征与真实端元特征的对比

图8 不同算法在Urban数据集的丰度图对比

5 结束语

本文提出一种新的高光谱解混算法L21NMF-SSR。首先，使用L21范数替换标准NMF中的F范数，对模型进行了改进。为了充分利用高光谱数据的丰度先验信息和空间结构信息，本文在L21NMF模型中加入了双重加权稀疏约束和子空间结构正则项，增强了丰度的稀疏性并捕获了全局空间结构信息。模拟数据、Jasper Ridge数据和Urban数据的实验结果均证明，L21NMF-SSR的性能优于其他5种算法，而且该算法具有较好的去噪能力和更强的鲁棒性。

然而，该方法仍有上升的空间，比如：(1)L21NMFSSR使用的是单层NMF，未考虑深层结构的信息；(2)算法探索了丰度的先验信息，却忽略了对端元的约束。因此在未来的工作中，可以尝试解决这些问题。