基于Copula函数研究莪术-三棱药对治疗“气滞血瘀”证的方剂剂量耦合效应
2022-05-31林丽婷王继森高天慧杨青松代文东
林丽婷,罗 霄,王继森,廖 婉*,高天慧,杨青松,杨 鹏,林 薇*,代文东,孔 颖
基于Copula函数研究莪术-三棱药对治疗“气滞血瘀”证的方剂剂量耦合效应
林丽婷1,罗 霄2#,王继森2,廖 婉1*,高天慧1,杨青松1,杨 鹏1,林 薇1*,代文东3,孔 颖3
1. 成都中医药大学 西南特色中药资源国家重点实验室,药学院,智能医学学院,四川 成都 611137 2. 成都市药品检验研究院,国家药品监督管理局中药材质量监测评价重点实验室,四川 成都 610045 3. 四川全泰堂中药饮片有限公司,四川 遂宁 629000
构建Copula函数,研究莪术-三棱药对治疗“气滞血瘀”证的方剂剂量耦合效应。从自建方剂数据库中收集治疗“气滞血瘀”证并含莪术-三棱药对的中医方剂,对其中莪术剂量和三棱剂量进行数据处理和检验,从阿基米德Copula函数族、椭圆Copula函数族中选择出最佳的Copula函数建立数学模型,描绘联合分布函数图,测算Kendall秩相关系数和Spearman秩相关系数,监测莪术剂量和三棱剂量数据间的相关性。整理归纳出505首方剂。Gaussian Copula函数模型能较好地反映莪术剂量和三棱剂量之间的相关性,莪术剂量和三棱剂量的Kendall秩相关系数为0.225 6,Spearman秩相关系数为0.333 0,说明莪术剂量和三棱剂量之间具有较强的非线性关系,且呈正相关,当剂量增加时,两者之间的耦合效应会增强。基于Copula函数模型,研究莪术-三棱药对在中医方剂配伍中的剂量相关性,从数据挖掘和数理统计角度为传统经典药对相须为用提供依据,为研究中药药对在中医药方剂配伍中的剂量关系提供新思路。
莪术-三棱药对;气滞血瘀;Copula函数;剂量相关性;耦合效应
药对又称对药,是中医临床遣药组方的经典配伍形式,是方剂的最小组成单位,也是连接中药和方剂的重要桥梁。莪术和三棱药性相通,均具有行气破血、消积止痛的功效[1]。莪术为气中之血药,善破气中之血,三棱为血中之气药,长破血中之气,故二者在中医临床用药上常常相须配伍,使破血行气之功倍增,行一身之气血,散一切瘀血气结。莪术-三棱二药配伍使用首见于《经验良方》中三棱丸[2]。“莪术汤”“京蓬术丸”“棱莪散”等经典方也均用此药对。《医林改错》有言:“药味要紧,分量更要紧”。在中医方剂组方配伍研究中,剂量对于临床功效的发挥至关重要,不同剂量的药物配伍产生的结果可能差异性较大,说明了中药剂量在中医“辨证论治”体系中的重要性[3]。
Copula函数是由Sklar[4]最早提出,是一类将联合分布函数与边缘分布函数连接在一起的函数,可以用于捕捉变量间非线性、非对称以及尾部相关关系。对于二元Copula函数来说,令(,) 为二元联合分布函数,如果其边缘分布为() 和(),那么就存在着一个Copula函数(,),满足关系(,)=[(),()]。如果() 和() 均为连续函数,那么(,) 唯一存在[5]。Copula函数包含多个分布族,较为常见的有阿基米德函数族(Gumbel Copula函数、Clayton Copula函数、Frank Copula函数)、椭圆Copula函数族(Gaussian Copula函数、t-Copula函数)。耦合是指一个别系的功效输出与另一个别系的功效输出相配合,体系之间产生功能互补、彼此交融、彼此促进的联动[6],与中药配伍规律中的“相须、相使”有异曲同工之处。本研究从自建方剂库中收集整理含莪术-三棱药对治疗“气滞血瘀”证的中医药方剂,寻找拟合后的Copula函数模型,对方剂中莪术-三棱药对剂量进行数学描述,研究莪术-三棱药对剂量与“气滞血瘀”证的相互关系,深入认识其配伍规律。利用Copula函数,从数据挖掘和数理统计2个角度探究莪术-三棱经典药对剂量的耦合效应,从剂量相关性的角度计算莪术-三棱药对的秩相关系数,探索中药“相须、相使”配伍关系的数理模型,为研究中药药对剂量关系提供新思路,也为中医药临床应用提供科学依据。
1 数据来源
收集宋、金、元、明、清至近现代的经典方书、名医所著方书、地方中药成方选集、地方用药规范、《中国药典》等,如宋代《圣济总录》《太平惠民和剂局方》《太平圣惠方》,金代《宣明论方》《内外伤辨》《兰室秘藏》,元代《丹溪心法》《御药院方》《医方大成》,明代《普济方》《古今医鉴》《寿世保元》,清代《医学衷中参西录》《郑氏家传女科万金方》《医方简义》,近代《幼科金针》,现代历版《中国药典》《全国中药成药处方集》等,建立方剂库。
为保证获得具有代表性和准确性的莪术和三棱剂量指标,从方剂库筛选方剂的条件包括:①方剂中包含莪术、三棱2味药物,主治为“气滞血瘀”证;②方剂中药物的剂量描述准确。从符合条件的505首方剂中提取莪术-三棱药对剂量数据,由于药方单位不统一,不同年代的计量单位与现代计量单位的换算关系不同,按照现代计量换算原则对药对剂量进行换算统一[7-8],见表1,方剂示例见表2。
2 数据处理和检验
2.1 数据处理
对筛选出的治疗“气滞血瘀”证的莪术剂量和三棱剂量进行换算,经换算后其剂量分布见图1。本研究使用Matlab R2020a和SPSS 26.0进行数据分析和模型拟合。
表1 方剂剂量单位换算原则
Table 1 Principle of unit conversion of prescription dose
传统计量单位换算成标准单位/g宋金元明清近代 1斤661.00661.00661.00596.80596.80500.00 1两 41.31 41.31 38.10 37.30 37.30 31.25 1钱 4.13 4.13 3.81 3.73 3.73 3.12 1分 0.41 0.41 0.38 0.37 0.37 0.31
表2 含莪术-三棱药对的经典方剂示例
Table 2 Some prescriptions containing Curcuma Rhizoma and Sparganii Rhizoma and their dosages
序号方名朝代莪术剂量/g三棱剂量/g 1化癖丸宋20.65520.655 2分气丸宋30.00030.000 3三棱消积丸金21.00021.000 4积气丹金41.31041.310 5消块丸元 5.720 5.720 6十膈气散元30.00030.000 7三棱丸明13.05513.055 8大七气汤明45.00045.000 9棱莪散清11.19011.190 10化气汤清15.00015.000 11三棱散近代32.81032.810 12阿魏化痞膏现代20.00020.000

图1 莪术-三棱药对的剂量分布
根据方剂剂量单位换算原则,依据换算后的剂量进行描述性统计分析,分别计算其中位数(M)、四分位数间距(IQR)、95%置信区间(confidence interval,CI),见表3。结果表明,“气滞血瘀”证的方剂组别里,莪术剂量多集中在19.76~21.99 g,中位数为18.65 g,三棱剂量多集中在19.89~22.15 g,中位数为18.65 g。
表3 莪术-三棱药对剂量的描述性统计
Table 3 Descriptive statistics of Curcumae Rhizoma and Sparganii Rhizoma pair dosage
变量数量M (IQR)95% CI 莪术剂量50518.65 g(26.00)19.76~21.99 三棱剂量50518.65 g(26.00)19.89~22.15
2.2 数据正态性检验
针对治疗“气滞血瘀”证的莪术和三棱剂量,进行Kolmogorov-Smirnov检验,绘制数据的Q-Q图,见图2、3。结果表明,莪术剂量KS值为0.165、三棱剂量KS值为0.171,值均小于0.001,莪术和三棱的剂量数据均呈现出非正态的特征,判断数据不服从正态分布,在已知的分布中较难找到合适的分布进行拟合,需要使用非参数的方法来确定莪术和三棱剂量的分布。

图2 莪术剂量的Q-Q图

图3 三棱剂量的Q-Q图
2.3 数据拟合边缘分布
由于数据不服从正态分布,而非参数估计法是在经验分布和核分布估计的基础上展开,因Ksdensity函数常用于计算一维或二维核密度或分布估计,故本研究应用Ksdensity函数[4]分别计算莪术、三棱剂量的边缘分布。为避免经验分布函数因连续性及光滑度不好而引起误差,采用核分布函数来拟合经验分布函数,见图4、5。结果表明,莪术剂量和三棱剂量的核分布函数和经验分布函数拟合较好。

图4 莪术剂量核估计图
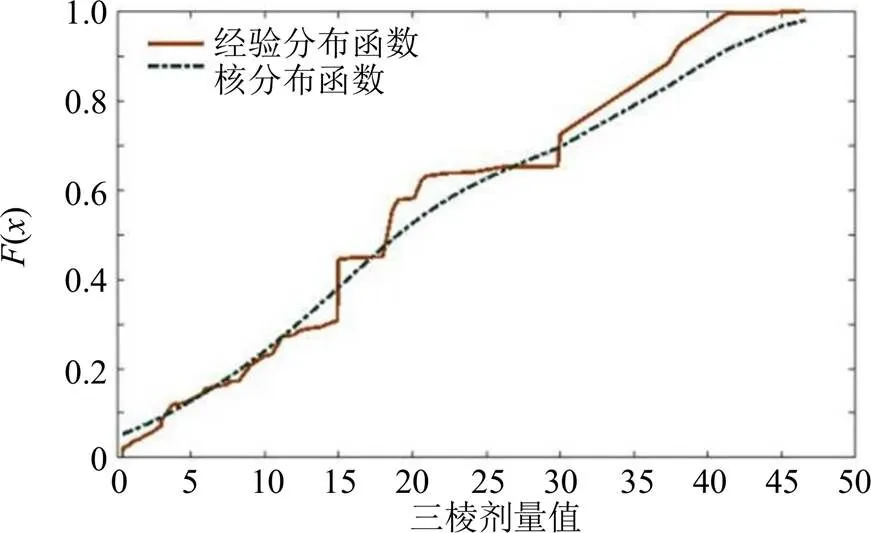
图5 三棱剂量核估计图
在确定各自边缘分布后,得到莪术剂量和三棱剂量(,)的二元分布直方图(图6、7),其中()、()。根据频数分布直方图和频率分布直方图可知,莪术剂量和三棱剂量尾部相关性较强。从频率分布直方图可以发现其数据均具有非对称的尾部特征,可采用Copula函数对莪术剂量与三棱剂量之间的非线性关系进行全面分析。
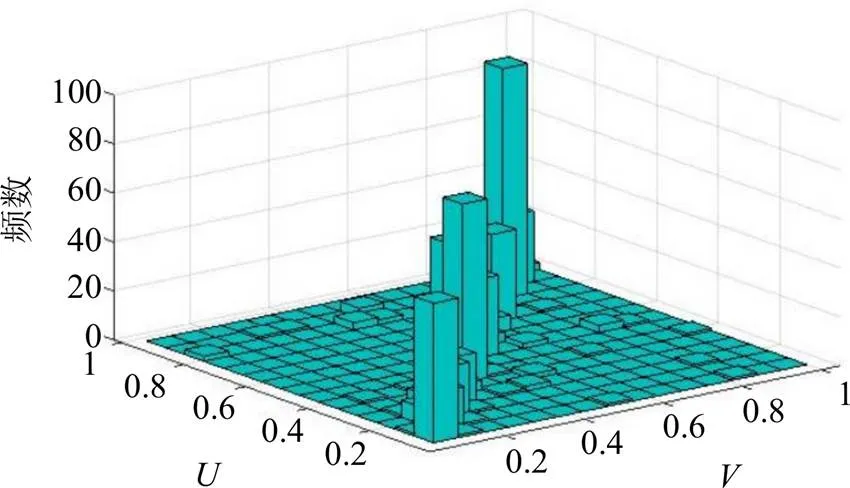
图6 莪术-三棱药对剂量的频数分布

图7 莪术-三棱药对剂量的频率分布
3 运用Copula函数分析药对剂量相关性
从阿基米德函数族(Gumbel Copula函数、Clayton Copula函数、Frank Copula函数)、椭圆Copula函数族(Gaussian Copula函数、t-Copula函数)中选择最佳的Copula函数,刻画莪术和三棱剂量之间的关系。通过平方欧式距离算法,将多种Copula函数与经验分布函数求解平方欧氏距离,在该标准下选取的最佳Copula函数就是其对应的经验Copula函数之间所得距离最短的Copula函数。
将治疗“气滞血瘀”证的505首方剂中莪术剂量群和三棱剂量群代入Copula函数,测算二者相应的平方欧式距离、Copula函数的参数估计值及相关系数,见表4。
结果表明,由于Gaussian Copula函数的平方欧式距离最小为0.004 3,参数估计值为0.347 0,故最佳函数取Gaussian Copula函数。Gaussian Copula函数Kendall秩相关系数为0.225 6,Spearman相关系数为0.333 0,说明莪术和三棱剂量之间有较强的非线性相关关系,且二者呈正相关,体现了协同效应。当莪术剂量和三棱剂量变化较大时,二者之间的协同效应会增强,即莪术的剂量增大,三棱的剂量也会明显增大。采用Gaussian Copula能较好地拟合莪术剂量和三棱剂量之间的关系,其表达式如下。
表4 莪术-三棱药对治疗“气滞血瘀”证的方剂剂量Copula函数相关参数
Table 4 Parameter estimation of Copula function on doseof Curcuma Rhizoma and Sparganii Rhizoma pair in treatment of “qi stagnation and blood stasis” syndrome
Copula函数平方欧氏距离参数估计Kendall相关系数Spearman相关系数 Clayton Copula0.012 41.194 40.373 90.531 1 Frank Copula0.008 32.795 00.289 10.423 6 Gumbel Copula0.008 71.350 50.259 50.376 8 Gaussian Copula0.004 30.347 00.225 60.333 0 t-Copula0.024 10.479 00.328 00.436 7
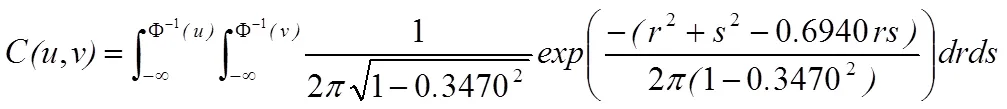
依据Gaussian Copula绘制莪术、三棱剂量的联合分布函数Copula(,),其中莪术剂量的边缘分布函数为(),三棱剂量的边缘分布函数为()。密度函数的尾部拥有更厚的形态特征,可以更好地捕捉莪术和三棱剂量之间的尾部相关性特征,说明采用Gaussian Copula函数建立的关于莪术和三棱剂量的模型,能较好地反映莪术和三棱剂量之间的秩相关性,见图8、9。
4 讨论
4.1 莪术-三棱药对剂量与“气滞血瘀”证的关系
药对衍生于“七情和合”的中医理论,是复方的重要组成部分。两药和合、搭配巧妙,很好地诠释中药“合群妙用”之特点,中药配伍之核心[9]。“中医不传之秘在量上,中医治病的巧处在量上”,中药剂量一直被视为方家的“不传之秘”,是中医配伍用药的精髓所在,直接影响组方临床疗效,因此找出药对剂量配伍的规律,揭示中药临床剂量的神秘面纱至关重要。
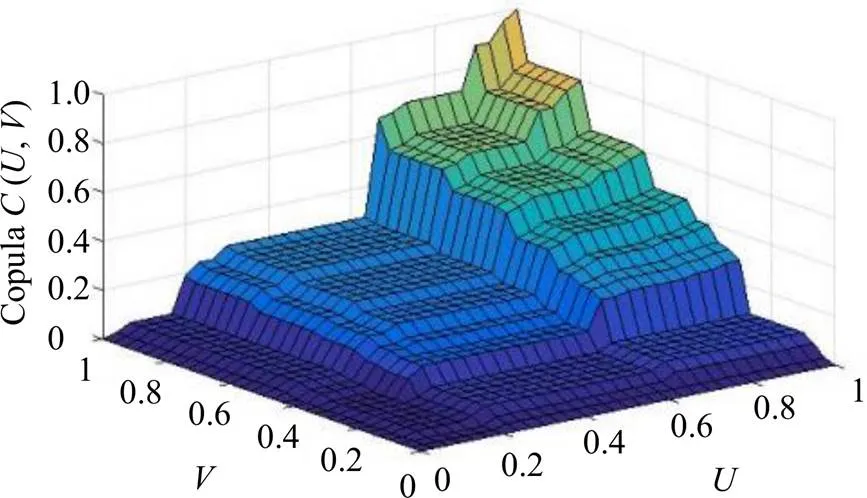
图8 莪术-三棱药对剂量的Copula联合分布函数

图9 莪术-三棱药对剂量的Copula联合概率密度函数
“气滞血瘀”证是中医临床常见证候,中医认为气血是构成和维持人体生命活动的基本物质。病理上,无论是气滞无法推动血行,还是血瘀致使气行不畅,都可造成气滞血瘀发生[10]。现代研究表明,“气滞血瘀”证的病机与现代临床微循环障碍[11]、血液流变学改变[12]、炎症[13]、凝血-纤溶系统失衡[14]、血管内皮功能障碍[15]、血脂异常[16]和免疫功能紊乱[17]具有潜在联系,现代临床常表现为血栓[18]、动脉粥样硬化[19]、高脂血症[20]、原发性痛经[21]等疾病。莪术和三棱作为破血化瘀的代表药物,两药配伍具有抗纤维化[22-23]、抑制血管新生[24]、抑制炎症因子[25]、抑制细胞凋亡及增殖[26]、调节内分泌激素水平[27]、抗动脉粥样硬化[28]、抗血栓[2]、抗肿瘤[29]等作用,在治疗子宫肌瘤[30]、卵巢囊肿[31]、肝硬化[32]、慢性胃炎[33]、慢性肾病[34]、肺纤维化[35]等方面具有显著的协同增效作用。
4.2 Copula函数分析莪术-三棱药对的剂量耦合效应
数据挖掘是从大量的、模糊的、随机的数据中提取有价值的信息和知识的过程,是一种随着信息化时代诞生的新兴数据处理技术,融汇了人工智能、模糊数学、模式识别、数据库、数理统计等多种技术方法[36]。与传统数据处理方法不同,数据挖掘能以线性、非线性以及模糊、多维度的方式解析数据,又能进行高维度的知识整合,可以反映多维数据之间的相互映射关系,在中医药领域研究中的可行性和适用性已经得到众多研究者的认可[37]。Copula函数模型已经用于分析中药有效成分群谱效及临床中西药联合用药的剂量关系[38],如李智慧等[39]通过构建适合的二元Copula函数模型,对中药有效成分群指纹图谱与药物活性进行分析,探索简单易行的中药质量控制方法。Gasparini[40]在Copula函数的基础上提出了一类新的风险函数,评估临床中西医联合治疗时相关性。Yin等[41]提出了一种基于Copula模型的贝叶斯自适应剂量发现设计,以解释2种或多种药物组合使用时剂量的协同作用。
本研究通过对数据进行正态性检验,发现莪术-三棱药对剂量数据均不符合正态分布,呈非线性、非对称的趋势。通过讨论莪术-三棱药对治疗“气滞血瘀”证的方剂所对应的频数图和频率图,利用Copula函数得到联合分布函数及概率密度函数。莪术与三棱组方多以1∶1的剂量形式出现。通过Copula函数模型分析结果表明,在治疗“气滞血瘀”证方剂中,莪术剂量和三棱剂量均是正相关,当二者的剂量变化较大时,两者之间的耦合效应会增强,即莪术的剂量增大时,三棱的剂量也会明显增大。莪术-三棱药对的现代研究也大多是针对配伍前后药物的物质基础分析、化学成分、药理药效的变化,均未对组方配伍剂量深入探讨,故应用Copula函数研究莪术-三棱药对的剂量耦合效应具有一定的意义。莪术-三棱药对剂量存在其他不同配比对临床疗效也有较大影响,且药对的耦合效应不仅体现在药理药效方面,还体现在药代、药化等方面,深入了解其剂量组方配比,阐释配伍规律,揭示配伍机制,这也是下一步要研究的重点。
中医药是中华民族在数千年的发展过程中产生的瑰宝,丰富的中医药学理论是中医药学术文脉与思想的重要载体,疗效确切的临证方剂是创新发展中医药学的重要源泉。通过归纳分析药对的剂量使用规律,不仅可以奠定中药在临床应用中从剂量变化到效应变化的研究基础,也可为现代中医临床用药提供更加丰富的剂量参考和依据,促进中医临床合理用药。Copula函数模型能科学阐释传统经典药对的配伍规律,本研究通过讨论莪术-三棱药对的剂量耦合效应,从剂量相关性的角度测定莪术-三棱药对的秩相关系数,探索中药“相须、相使”配伍关系的数理模型,为挖掘古方数据和指导传统医学临床用药研究的一种新模式,为研究中药药对剂量关系提供新思路。
利益冲突 所有作者均声明不存在利益冲突
[1] 中国药典 [S]. 一部. 2020: 13, 286.
[2] 唐荣霜, 石洲, 李晋奇, 等. 三棱莪术药对的研究进展 [J]. 实用医院临床杂志, 2021, 18(5): 226-229.
[3] 汪琼. 基于数据挖掘的国医大师应用解表类药物的剂量及相关研究 [D]. 武汉: 湖北中医药大学, 2017.
[4] Li D X. On default correlation [J]., 2000, 9(4): 43-54.
[5] Aas K, Czado C, Frigessi A,. Pair-Copula constructions of multiple dependence [J]., 2009, 44(2): 182-198.
[6] 陈雪龙, 姜坤. 基于贝叶斯网络的并发型突发事件链建模方法 [J]. 中国管理科学, 2021, 29(10): 165-177.
[7] 陈颖. 古方剂量规范处理和分析方法研究 [D]. 成都: 成都中医药大学, 2006.
[8] 赵晓军. 中国古代度量衡制度研究 [D]. 合肥: 中国科学技术大学, 2007.
[9] 王胜鹏, 陈美婉, 王一涛. 中药药对的系统研究(I): 理论与物质基础研究 [J]. 世界科学技术—中医药现代化, 2012, 14(2): 1317-1321.
[10] 何浩强, 陈光, 高嘉良, 等. 气滞血瘀证生物学基础研究进展 [J]. 中华中医药杂志, 2019, 34(9): 4167-4171.
[11] 王婷婷, 贾乘, 陈宇, 等. 大鼠气滞血瘀证模型的建立及影响因素分析 [J]. 中国中药杂志, 2012, 37(11): 1629-1633.
[12] 刘剑刚, 史大卓. 影响血液流变学的活血化瘀中药药物研究 [J]. 中国血液流变学杂志, 2004, 14(1): 133-137.
[13] 胡文娟, 赵凤达, 张秉韬, 等. 不同血瘀证亚型血小板活化及炎症反应改变的实验研究 [J]. 世界中西医结合杂志, 2011, 6(11): 931-934.
[14] 孔令钧, 李鲁扬, 唐占府. 老年气滞血瘀、气虚血瘀患者与CD62p、CD63及TSP关系的临床观察 [J]. 中国中西医结合杂志, 2001, 21(8): 588-590.
[15] 宁天一, 王婷婷, 姜静, 等. 气滞血瘀证大鼠NO/NOS体系的变化 [J]. 世界中医药, 2013, 8(1): 71-73.
[16] 余冬严, 魏康伯, 沃兴德. 血府逐瘀汤对气滞血瘀型高脂血症降脂作用的临床观察与实验研究 [J]. 中西医结合杂志, 1988, 8(10): 601-603.
[17] 陈志伟, 顾美华, 邓迎苏, 等. 206例系统性红斑狼疮患者中医证型与免疫学指标的相关性研究 [J]. 中医杂志, 2000, 41(4): 234-236.
[18] 石志芸, 施赛珠, 陈剑秋, 等. 中医血瘀证与血栓相关分子标志物的研究 [J]. 中医研究, 2003, 16(6): 21-23.
[19] 胡坤, 何浩强, 朱爽, 等. 冠状动脉粥样硬化性心脏病气滞血瘀证客观化研究现状 [J]. 中国中医药信息杂志, 2021, 28(2): 132-137.
[20] 甄翔兴, 安冬青. 高脂血症中医证型与复方治疗的研究进展 [J]. 中西医结合心脑血管病杂志, 2017, 15(7): 812-815.
[21] 勾明慈. 王昕教授治疗气滞血瘀证原发性痛经临床经验总结 [D]. 沈阳: 辽宁中医药大学, 2018.
[22] 谭静, 林红强, 王亚茹, 等. 三棱的化学成分、药理作用及临床应用研究进展 [J]. 特产研究, 2018, 40(4): 109-113.
[23] 徐速, 曾莉. 三棱丸方对肠上皮细胞上皮间质转化TGFβ1/Smads信号通路的影响 [J]. 辽宁中医杂志, 2017, 44(1): 125-127.
[24] 翁维良, 牛宗新. 活血化瘀治疗疑难病[M]. 北京: 学苑出版社, 1993: 65-67.
[25] 程杰, 曹秀莲, 曹文利, 等. 三棱莪术配方颗粒配伍对子宫内膜异位模型大鼠的改善作用及机制初探 [J]. 中药药理与临床, 2018, 34(4): 134-138.
[26] 王振兴, 李水芹, 赵梓亦, 等. 三棱、莪术提取物联合热疗对结肠癌SW620细胞凋亡及迁移、侵袭能力的影响 [J]. 中国药房, 2018, 29(24): 3386-3391.
[27] 付煜, 徐秋霞, 张黎, 等. “三棱-莪术”组分配伍对子宫肌瘤大鼠下丘脑和垂体激素的影响 [J]. 中药与临床, 2020, 11(2): 31-36.
[28] 李杨, 周岚, 汪典, 等. 不同剂量活血、破血中药对动脉粥样硬化小鼠主动脉PTGS2、PADI4、ITGAM基因表达的影响 [J]. 疑难病杂志, 2016, 15(11): 1182-1186.
[29] 张磊, 程健, 余莹, 等. 活血祛瘀药对三棱-莪术治疗胃癌的网络药理学作用机制研究 [J]. 浙江中医药大学学报, 2020, 44(8): 773-782.
[30] 肖红妮, 刘志杰. “三棱-莪术”组分配伍介导PI3K-AKT通路治疗大鼠子宫肌瘤的研究 [J]. 世界中医药, 2019, 14(9): 2267-2271.
[31] 沈东成, 徐秋霞, 余舒鹏, 等. “生三棱-生莪术”配伍对卵巢囊肿大鼠C3、IGG、FSH、TNF-α的影响 [J]. 现代中医药, 2016, 36(4): 75-79.
[32] 赵晓威, 尚尔寿. 三棱莪术汤为主治疗肝硬化腹水40例 [J]. 湖南中医药导报, 2001, 7(12): 590-606.
[33] 赵刚, 邹迪新. 三棱莪术粉治疗62例慢性萎缩性胃炎的临床疗效 [J]. 当代医药论丛, 2014, 12(11): 192-193.
[34] 赵延栋, 李夏玉, 王云卿, 等. 益气养阴活血祛瘀法治疗慢性肾脏病1~4期慢性肾功能不全临床研究 [J]. 新中医, 2020, 52(8): 97-99.
[35] 王英豪, 姚欣, 邱颂平, 等. 破血化瘀药三棱莪术对大鼠肺纤维化干预作用的实验研究 [J]. 中国中医药科技, 2011, 18(3): 188-189.
[36] 周雯静, 金周慧, 刘灵力. 数据挖掘在中医药研究中的应用述评 [J]. 中国中医药信息杂志, 2014, 21(10): 131-133.
[37] 聂佳, 邓都, 雄呷, 等. 数据挖掘技术研究民族医药传统用药经验模式探讨 [J]. 中华中医药杂志, 2015, 30(3): 926-927.
[38] 林薇, 赵荷, 郝怡雯, 等. 基于Copula函数研究柴胡-白芍药对在治疗“肝郁血虚”方剂中的剂量相关性[J].中草药, 2021, 52(13): 4007-4013.
[39] 李智慧, 陆涛, 杨中林, 等. 基于Copula函数的中药有效成分群谱效分析 [J]. 中国卫生统计, 2013, 30(5): 650-653.
[40] Gasparini M. General classes of multiple binary regression models in dose finding problems for combination therapies [J]., 2013, 62(1): 115-133.
[41] Yin G S, Yuan Y. Bayesian dose finding in oncology for drug combinations by Copula regression [J]., 2009, 58(2): 211-224.
Dose coupling effect ofandpair in treatment of “stagnation and blood stasis” syndrome based on Copula function
LIN Li-ting1, LUO Xiao2, WANG Ji-sen2, LIAO Wan1, GAO Tian-hui1, YANG Qing-song1, YANG Peng1, LIN We1, DAI Wen-dong3, KONG Ying3
1. State Key Laboratory of Southwestern Chinese Medicine Resources, School of Pharmacy, School of Intelligent Medicine, Chengdu University of Traditional Chinese Medicine, Chengdu 611137, China 2. Key Laboratory of Quality Monitoring and Evaluation of Chinese Medicinal Materials, National Medical Products Administration, Chengdu Institute for Drug Control, Chengdu 610045, China 3. Sichuan Quantaitang Chinese Herbal Slices Co., Ltd., Suining 629000, China
To study the dose coupling effect of Ezhu () and Sanleng () pair in the treatment of “stagnation and blood stasis” by constructing Copula function.The traditional Chinese medicine prescriptions containingandpair for the treatment of “stagnation and blood stasis” syndromewere collected from the self-established prescription database. The data of the dosage ofandwere processed and tested. The best Copula function was selected from Archimedes Copula function family and elliptic Copula function family to establish mathematical model and depict the joint distribution function diagram. Kendal and Spearman rank correlation coefficients were calculated and correlation between the dose data ofandwas monitored.A total of 505 traditional Chinese medicine prescriptions containingandwere collected from the self-established prescription database. The dosage correlation betweenandcould be better reflected by Gaussian Copula function model. The correlation coefficient of Kendall rank and Spearman rank ofdose anddose were 0.225 6 and 0.333 0, respectively, which indicates that there was a strong nonlinear correlation betweendose anddose. And the correlation was positive. The coupling effect between the two increased with the increase of dose.Based on the Copula function model, the dose correlation ofandpair in the compatibility of traditional Chinese medicine prescriptions was studied. From the perspective of data mining and mathematical statistics, it provides a basis for the mutual promotion use of traditional drug pair and new ideas for the study of the dose relationship of traditional Chinese medicines in the compatibility of traditional prescriptions.
anddrug pair;stagnation and blood stasis; Copula function; dosage correlation; coupling effect
R283.21
A
0253 - 2670(2022)11 - 3425 - 07
10.7501/j.issn.0253-2670.2022.11.019
2022-02-03
四川省科技计划重点研发项目(2020YFN0152);四川省首批中医药学科建设重点项目(药用植物学,川中医药函[2020]84号)
林丽婷,女,在读硕士,研究方向为中药制剂新技术、新剂型和炮制研究。Tel: 15928086785 E-mail: 1069590640@qq.com
廖 婉,女,博士,教授,硕士生导师,主要从事中药炮制工艺与机制、中药药剂研究。E-mail: liaowan@cdutcm.edu.cn
林 薇,女,讲师,主要从事中医药统计与应用研究。E-mail: linwei@cdutcm.edu.cn
#共同第一作者:罗 霄,男,副主任中药师,主要从事中药材质量监测评价及标准研究。E-mail: 76209608@qq.com
[责任编辑 潘明佳]
